2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
水平气井比直井排水采气更加困难,其连续携液研究需要考虑倾斜井段的倾斜角度和水平井段的影响。国内外在这方面的研究大多针对垂直管[1-7]和水平管[8-10],针对倾斜管的携液研究[11-13]还不成熟。国内外学者建立了倾斜管临界携液流量预测理论模型或半经验模型[14-17],目前主流观点有两种,一种是基于液滴模型假设, 认为排出气井积液所需的最低条件是使气流中的最大液滴能连续向上运动;另一种是基于液膜模型假设,认为液膜的反向流动是导致积液的主要原因,两类模型的携液机理完全不同,但在现场应用时都存在一定误差。因此,本文开展了水平气井井筒气液两相流实验,对水平井井筒气液两相流的特性进行观察和分析,对比直井段、倾斜井段、水平井段的携液能力,并利用测试数据对水平井连续携液液滴模型和液膜模型进行评价。
1 实验装置与实验方法为了研究水平井的连续携液与积液情况,比较水平井的水平井段、垂直井段和倾斜井段携液能力的差异,设计制作了水平井井筒气液两相流模拟实验装置,实验流程如图 1所示。实验系统由进气系统、进水系统、实验管段系统与测量系统4部分组成。实验管段主体部分由有机玻璃管组成,垂直段长6.0 m,倾斜段长6.0 m,水平段长10.0 m,采用ϕ40 mm ×5 mm的有机玻璃模拟油管,ϕ75 mm ×8 mm的有机玻璃管模拟套管;进气系统由空气压缩机、储气罐和液压管线组成;进水系统包括储罐、计量水箱和管线;测量系统包括压力传感器、压差传感器、气体流量计、数据采集模块以及计算机,可实现实时记录。
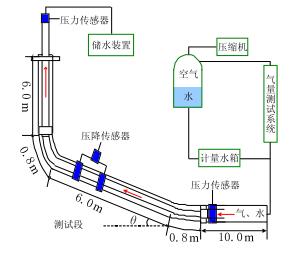 |
| 图1 水平气井连续携液实验流程 Fig. 1 The experimental process of continuous removal in horizontal gas well |
实验中通过改变注入气量,观测不同倾斜角θ(28°~72°)下实验管段中的气液两相流型变化和液体(液滴、液膜)的携带情况。实验过程中保持注入水压不变,调节注入气量直至实验管段中达到稳定的临界携液状态(液膜在重力作用下短暂停留,而后又在气流的作用下重新携带上升时),记录此时的注入气流量、注入水流量、实验段压力、压差和温度等相关数据。一组实验后再改变实验管段中压力重复实验,以得到不同井底流动压力下的临界携液流量数据。
2 实验现象 2.1 倾斜管段的携液能力最差 2.1.1 倾斜管段达临界携液时,各井段的流态实验观察到倾斜管段达到临界携液状态时,水平管段与垂直管段的携液流速大于其临界携液流速。
垂直管段大部分液体以液膜的形式沿管壁向上运动,少部分液滴分散在气流中,以环状流的形式携带液体,液膜厚度薄,液滴直径较大;倾斜管中液滴不会一直沿井筒中心线上升,而是慢慢运移至油管壁,液滴到达管壁之后与液膜聚集,并最终破碎,液滴无法长时间稳定存在,液相主要以液膜的形式被携带,管底液膜基本无滑脱现象,呈现偶尔短暂停顿后继续上升的现象,部分液体直接被携带至垂直管,而管底部分厚液膜会停滞后被携带上升,此时的流型为环状流,如图 2所示;而水平管的携液流速大于其临界携液流速,大部分液体以液流的形式沿水平管底部运动,液相被气流卷升形成大量液滴。
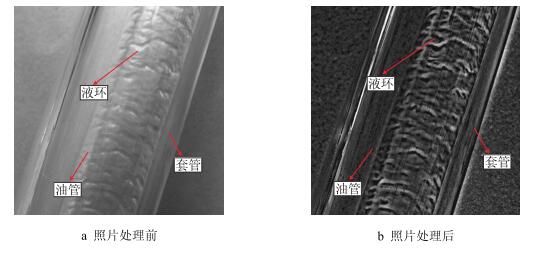 |
| 图2 倾斜管临界携液时为环状流 Fig. 2 Annular flow of critical liquid-carrying in the inclined tube |
实验观察到水平管段达到临界携液状态时,倾斜管的携液流速明显小于临界携液流速,垂直管段的携液流速大于临界携液流速。
水平管段液体以液流的形式沿水平管底部运动,液流连续移动,被气流卷升形成的液滴,与倾斜管段达到临界携液状态时相比,液滴数量明显减少;倾斜管管底液膜存在明显的滑脱现象,呈现来回下降又上升的过程,部分液体直接被携带至垂直管,而部分管底厚液膜会回流至倾斜管末端,然后重新被携带上升;垂直管段以环状流的形式携带液体,与倾斜管段临界携液时的状态相比,液膜厚度明显增大,液滴直径也增大。
2.1.3 垂直管段达临界携液时,各井段的流态垂直管段为临界携液状态时,水平管段与倾斜管段的携液流速明显小于其临界携液流速。
垂直管一般以环状流的形式携带液体,越接近临界携液点,液膜厚度越厚,液滴直径越大,大部分液体以液膜形式沿管壁向上移动,液膜偶有停顿,但无回流,与水平管段达到临界携液时相比,液膜厚度增加,上升速度减缓,此时的流型为环状流;水平管管底液膜厚度会增加,且移动速度变慢。受倾斜管段回落液体的影响,水平管段也时常发生液相回流;倾斜管管底液膜存在明显的滑脱现象,呈现来回下降又上升的过程,部分液体直接被携带至垂直管,而部分管底厚液膜会回流至倾斜管末端,然后重新被携带上升,与水平管段临界携液时相比,底部液膜的回流更加频繁和迅速,且回流的液量也会增加。
由上述实验现象可知,水平气井的水平井段、倾斜井段和垂直井段中,垂直井段的临界携液能力最强,倾斜井段的携液能力最差,临界携液气量最大。因此,在研究气藏水平井的连续携液问题时需要分析斜井段的临界携液流速,以得到水平气井临界携液产气量。
2.2 倾斜管中液滴无法长时间稳定存在,液相主要以液膜的形式被携带气相以流速ug沿倾斜井筒向上时,液滴在井筒运动过程中受气流对其施加的曳力R、浮力以及自身重力G的共同影响,经过受力分析(图 3)可知,在垂直方向,浮力F浮以及曳力R的垂直分量Rv与液滴的自身重力可达到平衡,但液滴在水平方向上只有曳力R的水平分量Rh,其受力始终不平衡,因此液滴不会一直沿井筒中心线平稳上升,而是在上移的同时,慢慢运移至油管壁,液滴到达管壁之后与液膜聚集,并最终破碎,液滴的运动轨迹如图 4所示。换言之,液滴无法在倾斜井筒中长时间稳定存在,液相主要以液膜的形式被携带。
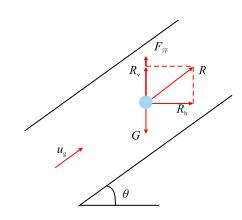 |
| 图3 倾斜井筒中液滴受力分析 Fig. 3 Force analysis of droplet in inclined tube |
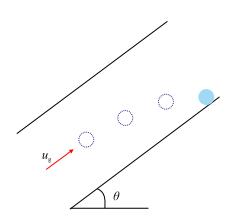 |
| 图4 液滴在倾斜管中的运动轨迹 Fig. 4 Trajectory of droplet in the inclined tube |
为了确定倾斜管液膜向上推移的临界气流速,开展了气液两相流模拟实验,测试了不同气流量、液流量下的压降梯度,分析了环状流、搅动流的压降特征。以压降特征作为依据进行了倾斜管连续携液实验,测试不同倾斜角下的临界携液气流速,分析了角度对临界气流速的影响。
3.1 倾斜管流动特征实验测试了不同液流速、气流速下倾斜管段的压降梯度,如图 5所示。在低流速区域,随表观气流速的增加,压力梯度逐渐降低;在高流速区域,压力梯度随表观气流速的增加而增加;当表观气流速为12~15 m/s时,压力梯度最小。对于这种现象可从管壁对液膜的剪切力方向及大小、以及气芯中液体夹带量与气流速的关系进行解释。
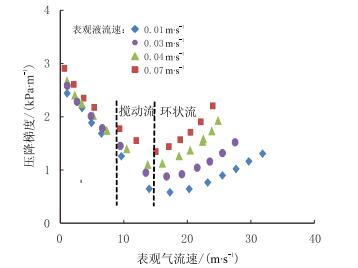 |
| 图5 倾斜角为72°时压力梯度与表观气、液流速的关系 Fig. 5 Relation of pressure gradient with superficial gas and liquid velocity in 72° |
在高气流速区域,气/液膜同向流动,气相流速ug、液膜流速uf均向上,此时流型为环状流,液膜受力情况如图 6所示,液膜在倾斜井段井筒运动过程中受气流对其施加的剪切力τi、管壁剪切力τw,自身的重力及管壁对其的支持力。管壁剪切力τw方向为沿管壁向下,气相流速ug越大,剪切力τi越大,摩阻压降越大;同时气相流速ug越大,气芯中液体夹带量越大,气液混合物密度越大,平行于管壁方向的重力压力降越大,垂直于管壁方向的重力分量也会增加,进一步增大管壁对流体的剪切力τw。因此,随着气相流速的增加,管中流体的压力梯度也逐渐增大。
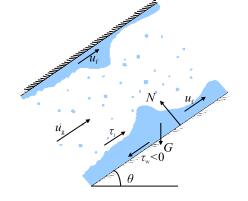 |
| 图6 同向环状流 Fig. 6 Cocurrent flow is annular flow |
在低气相流速区域,气/液膜逆向流动,即液膜产生回流,此时流型为搅动流,液膜受力情况如图 7所示。回流会造成液膜在管壁的短暂堆积,液膜厚度增大,当其增大到一定程度即会发生坍塌形成液滴分散在气相中。气相流速ug越小,液膜回流比例越大,气流夹带的液体量增大,气液混合物密度增加,重力压力降增加,故压降增大。且液膜回流比例越大,压降波动越大。
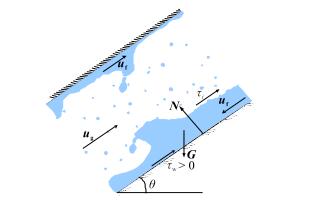 |
| 图7 逆向搅动流 Fig. 7 Counter current flow is churn flow |
当液膜流动方向处于由上向下或由下向上的临界状态时,流型为环状流,如果气流速继续降低,则会转变为搅动流,此时的状态即为环状流向搅动流转变的临界点。在该流动状态,液膜停滞不动,液膜流速uf为零。管壁与液膜间的剪应力τw为零,压力降最小,气流量在小范围内变化时,压降基本不变,此时的气相流速为临界携液流速。
以上分析可知,环状流与搅动流下的压降与气相流速的关系相差较大,环状流压降随气相流速的增加而增加,搅动流压降随气相流速的增加而降低,临界点压降最小,因此可分析压降与气相流速的关系确定流型是环状流或搅动流,如图 8所示,也可确定临界携液流速。
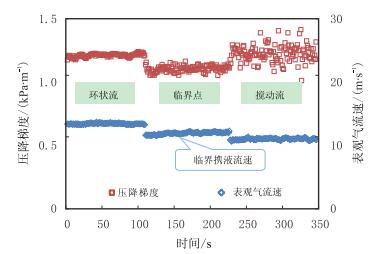 |
| 图8 压降梯度与表观气流速的关系 Fig. 8 Relation of pressure gradient with superficial gas velocity |
实验测试了不同倾斜角度(28°~72°)下,倾斜管段入口压力为20~90 kPa时的连续携液临界气相流速,图 9为不同压力下临界携液气相流速与倾斜角的关系图。从图中可知:
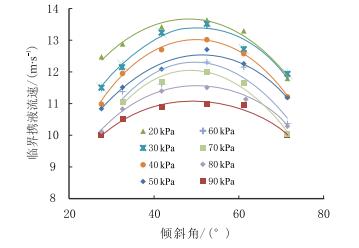 |
| (θ=0时,为水平管) (θ=0, horizontal) 图9 井底流压20~90 kPa时临界携液流速随倾斜角的变化关系 Fig. 9 Relation of critical liquid-carrying velocity with inclined angle in 20~90 kPa |
(1)倾斜角为50°左右临界携液流速达到最大;
(2)倾斜角小于50°时,随倾斜角度的增大,临界携液流速逐渐增大,随倾斜角的增大,增大速度逐渐变缓;
(3)倾斜角大于50°时,随着倾斜角的增大,临界携液流速逐渐减小。
4 倾斜管携液模型评价目前的携液模型主流观点有两种,一种是基于液滴模型假设,认为排出气井积液所需的最低条件是使气流中的最大液滴能连续向上运动;另一种是基于液膜模型假设,认为液膜的反向流动是导致积液的主要原因。
研究倾斜管段的临界携液时,液膜模型比液滴模型更为合理,主要理由如下:
(1)从理论分析出发,液滴在倾斜井段井筒运动过程中受气流对其施加的曳力、浮力以及自身重力的共同影响,经过受力分析(图 2)可知,液滴在水平方向上的受力始终不平衡,因此液滴不会一直沿井筒中心线上升,而是慢慢运移至油管壁,液滴到达管壁之后与液膜聚集,并最终破碎。换言之,液滴无法在倾斜井筒中长时间稳定存在。
(2)从实验现象出发,实验观察到临界连续携液发生在搅动流向环状流转化的流型区间,液滴生成后,在向上移动的同时,逐渐向管壁靠近,最终与管壁的液膜融合在一起,并不能稳定存在,倾斜管的液体主要以液膜模式被携带。
(3)实验观测到随倾斜角度的增大,临界携液流速先增大,再减小。以液滴为研究对象,受力平衡时,气相对于液滴的曳力与重力在运动方向上(即平行于管壁方向)的分量Gsinθ相等,重力G不变,θ在0~90° Gsinθ为θ的单调递增函数,曳力也为θ的单调递增函数,而曳力与气相流速成正比,因此,液滴模型计算出的临界携液流速随倾斜角的增加而增大,与实验结果不符;以液膜为受力分析对象,如图 7所示,sinθ为θ的单调递增函数,当倾斜角度θ增大,液膜的周向分布越均匀,最大液膜厚度δmax减小,即控制单元体的重力G′减小,G′为θ的单调递减函数,因此控制单元体在平行于管壁方向上的重力分量,即液膜向上运移的阻力G′sinθ并不是倾斜角θ的单调函数,与实验结果相符。
实验共测得213组数据,将液滴模型[14]和液膜模型[17]计算的携液流量与实验测试的气流量进行对比,结果如图 10和图 11所示,统计误差定义如下临界携液流量误差:
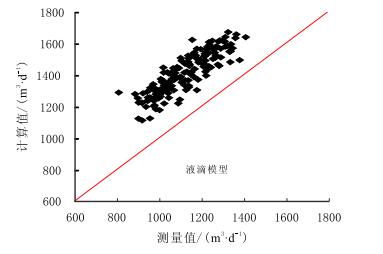 |
| 图10 液滴模型计算临界携液气流量与测试值对比 Fig. 10 Contrast of test and calculated value of droplet model |
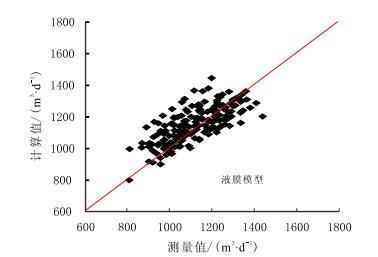 |
| 图11 液膜模型计算临界携液气流量与测试值对比 Fig. 11 Contrast of test and calculated value of film model |
eri=(计算值-实验值)/实验值
临界携液流量平均百分误差:
| $ {E_1} = \frac{1}{n}\sum {{e_{{\rm{r}}i}}} $ |
临界携液流量平均绝对百分误差:
| $ {E_2} = \frac{1}{n}\sum {\left| {{e_{{\rm{r}}i}}} \right|} $ |
临界携液流量标准偏差:
| $ {E_3} = \sqrt {\frac{{\sum {{{\left( {{e_{{\rm{r}}i}}-{E_1}} \right)}^2}} }}{{n-1}}} $ |
相关性能系数:
| $ {R_{{\rm{PF}}}} = \sum\limits_{i = 1}^3 {\left( {\left| {{E_i}} \right|-{{\left| {{E_i}} \right|}_{\min }}} \right)/\left( {{{\left| {{E_i}} \right|}_{\max }}-{{\left| {{E_i}} \right|}_{\min }}} \right)} $ |
从表 1可以看出,液滴模型计算的临界携液气流量整体性偏大25%~30%;液膜模型的计算结果与实验的吻合度较好,平均绝对百分误差为7.34%,计算值部分偏大,部分偏小,平均百分误差为4.12%,相对性能系数也更小,液膜模型更优。
| 表1 临界携液流量模型误差统计表 Table 1 Error statistics of critical liquid-carrying model |
(1)研制了水平气井连续携液模拟实验装置,进行垂直井段、水平井段和倾斜井段的携液实验,观测了气藏水平井中气水两相运动与流型变化情况并测试其临界携液气量。实验表明,倾斜管中所需的临界携液流速要大于水平管和垂直管,这说明水平井段和垂直井段对水平气井的连续携液影响不大,倾斜井筒中积液才是导致水平井积液的最主要因素。
(2)实验观察到倾斜管连续携液发生在搅动流向环状流转化的流型区间,液体主要以液膜形式携带,液滴无法长时间稳定存在,因此临界携液计算模型使用液膜模型更为合理。
(3)实验结果表明倾斜管的临界携液流速大于水平管和垂直管。倾斜角较小时,随倾斜角度的增大,携液流速有逐渐增大的趋势,增大速度逐渐变缓,在50°左右携液流速达到最大,然后随着倾斜角的增大,携液流速逐渐减小。
(4)利用实验数据对液滴模型和液膜模型进行对比评价,液膜模型的计算值与实验值的平均绝对百分误差为7.34%,平均百分误差为4.12%。推荐使用液膜模型计算水平气井临界携液流量。
| [1] | Turner R G, Hubbard M G, Dukler A E. Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells[J]. Journal of Petroleum Technology, 1969, 21 (11) : 1475 –1482. DOI:10.2118/2198-PA |
| [2] | Zabaras G, Dukler A E, Moalem-Maron D. Vertical upward cocurrent gas-liquid annular flow[J]. AIChE Journal, 1986, 32 (5) : 829 –843. DOI:10.1002/(ISSN)1547-5905 |
| [3] | Li M, Lei S, Li S. New view on continuous-removal liquids from gas wells[C]//SPE Permian Basin Oil and Gas Recovery Conference, Society of Petroleum Engineers, 2001. https://www.researchgate.net/publication/250090162_New_View_on_Continuous-Removal_Liquids_From_Gas_Wells |
| [4] | Lea J F, Nickens H V. Solving gas-well liquid-loading problems[J]. Journal of Petroleum Technology, 2004, 56 (4) : 30 –36. DOI:10.2118/72092-JPT |
| [5] | Van't Westende J M C, Kemp H K, Belt R J, et al. On the role of droplets in cocurrent annular and churn-annular pipe flow[J]. International Journal of Multiphase Flow, 2007, 33 (6) : 595 –615. DOI:10.1016/j.ijmultiphaseflow.2006.12.006 |
| [6] | 魏纳.气井积液可视化实验研究[D].成都:西南石油大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-10615-2008016754.htm |
| [7] | Moalem Maron D, Dukler A E. Flooding and upward film flow in vertical tubes-Ⅱ. Speculations on film flow mechanisms[J]. International Journal of Multiphase Flow, 1984, 10 (5) : 599 –621. DOI:10.1016/0301-9322(84)90084-3 |
| [8] | Flores A G, Crowe K E, Griffith P. Gas-phase secondary flow in horizontal, stratified and annular twophase flow[J]. International Journal of Multiphase Flow, 1995, 21 (2) : 207 –221. DOI:10.1016/0301-9322(94)00072-R |
| [9] |
雷登生, 杜志敏, 单高军, 等. 气藏水平井携液临界流量计算[J].
石油学报, 2010, 31 (4) : 637 –639.
Lei Dengsheng, Du Zhimin, Shan Gaojun, et al. Calculation method for critical flow rate of carrying liquid in horizontal gas well[J]. Acta Petrolei Sinca, 2010, 31 (4) : 637 –639. |
| [10] |
肖高棉, 李颖川. 水平井段连续携液理论与试验研究[J].
石油天然气学报, 2010, 32 (1) : 324 –327.
Xiao Gaomian, Li Yingchuan. Theory and experiment on the continuous liquid carrying in horizontal wells[J]. Journal of Oil and Gas Technology, 2010, 32 (1) : 324 –327. |
| [11] | Beggs H D. An experimental study of two-phase flow in inclined pipes[D]. University of Tulsa, 1972. http://www.sciencedirect.com/science/article/pii/0009250989850420 |
| [12] | Keuning A. The onset of liquid loading in inclined tubes[D]. Eindhoven Netherlands University of Technology, 1998. |
| [13] | Yuan G, Pereyra E, Sarica C. An experimental study on liquid loading of vertical and deviated gas wells[C]. SPE 164516, 2013 |
| [14] | Belfroid S P C, Schiferli W, Alberts G J N, et al. Prediction onset and dynamic behaviour of liquid loading gas wells[C]. SPE 115567, 2008. |
| [15] |
杨文明, 王明, 陈亮, 等. 定向气井连续携液临界产量预测模型[J].
天然气工业, 2009, 29 (5) : 82 –84.
Yang Wenming, Wang Ming, Chen Liang, et al. A prediction model on calculation of continuous liquid carrying critical production of directional gas wells[J]. Natural Gas Industry, 2009, 29 (5) : 82 –84. |
| [16] |
李丽, 张磊, 杨波, 等. 天然气斜井携液临界流量预测方法[J].
石油与天然气地质, 2012, 33 (4) : 650 –654.
Li Li, Zhang Lei, Yang Bo, et al. Prediction method of critical liquid-carrying flow rate for directional gas wells[J]. Oil & Gas Geology, 2012, 33 (4) : 650 –654. |
| [17] |
肖高棉, 李颖川, 喻欣. 气藏水平井连续携液理论与实验[J].
西南石油大学学报:自然科学版, 2010, 32 (3) : 122 –126.
Xiao Gaomian, Li Yingchuan, Yu Xin. Theory and experiment research on the liquid continuous removal of horizontal gas well[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (3) : 122 –126. |
 2014, Vol. 36
2014, Vol. 36

