测试压裂是在主压裂之前进行的小型压裂。它是通过进行一次小体积,且与主压裂相同的压裂液进行的不加砂压裂。测试压裂目的是获取与裂缝有关的地层物性参数,为制定和修改主压裂设计、指导施工及效果评价提供依据。图 1展示了测试压裂施工和停泵卸压阶段的井底压力历史。常规的测试压裂分析针对停泵前的裂缝扩展阶段,使用二维(PKN,KGD)或拟三维压裂模型,拟合净压力的方法计算水力裂缝几何参数[1-4]。停泵后受裂缝壁面压裂液滤失的影响井底压力递减,裂缝继续延伸,随后弹性闭合,当井底压力递减到地层闭合压力时,认为裂缝完全闭合。从停泵到裂缝闭合包含“裂缝延伸期”和“弹性闭合期”,此阶段的压力递减分析常使用G函数方法[5-11],求取地层滤失系数、闭合压力和闭合时间。裂缝闭合后(称为“闭合后期”)的压力递减不再受施工的影响,被视为仅与储层自身特性有关。闭合后期包括“闭合后拟线性流”和“闭合后拟径向流”两个流动阶段[12-14]。
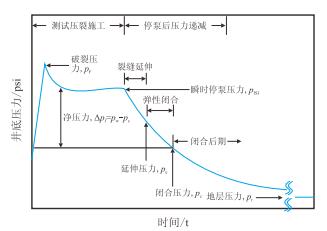 |
| 1psi=6.895 kPa 图1 测试压裂井底压力曲线 Fig. 1 Downhole pressure history of a fracture calibration test |
由于现有的压力递减分析方法都是针对某个流动阶段进行的,没有较为完整的流态诊断工具,也缺乏针对整个停泵后压力递减阶段的分析方法。本文提出一套停泵后压力递减数据的分析方法,诊断停泵后的多个流动阶段,综合延伸期、闭合期和闭合后期分析。通过东海低渗气田某测试压裂井的实例分析,运用井下压力监测数据[15-16]获取地层关键参数的方法,双对数诊断曲线分析压力递减数据。
1 压力递减模型 1.1 闭合期的压力方程根据质量守恒和体积平衡原理,Nolte模型[5]给出在裂缝弹性闭合期井底压力pw与时间函数G的关系式,如下
| $ \Delta p\left( {\Delta t} \right) = {p_{{\rm{ISI}}}}-{p_{\rm{w}}}(\Delta t) = \frac{{{C_{\rm{T}}}{H_{\rm{p}}}E'\sqrt {{t_{\rm{p}}}} }}{{{H^2}{\beta _{\rm{s}}}}}G\left( {t, {t_{\rm{p}}}} \right) $ | (1) |
其中
| $ G\left( {t, {t_{\rm{p}}}} \right) = \frac{4}{\pi }\left[{g(\frac{{\Delta t}}{{{t_{\rm{p}}}}})-{g_0}} \right] = \frac{4}{\pi }\frac{4}{3}\left[{{{(1 + \frac{{\Delta t}}{{{t_{\rm{p}}}}})}^{\frac{3}{2}}}-{{(\frac{{\Delta t}}{{{t_{\rm{p}}}}})}^{\frac{3}{2}}}} \right] $ | (2) |
当∆t/tp~1时,
| $ G\left( {t, {t_{\rm{p}}}} \right) = \frac{4}{\pi }\frac{4}{3}\left[{{{\left( {\frac{{\Delta t}}{{{t_{\rm{p}}}}}} \right)}^{\frac{3}{2}}}-1} \right] $ | (3) |
Clarslaw和Jaega热扩散模型[13]描述了一个表面恒温的半无限体,从开始与周围隔热到随后的热衰减过程。考虑到地层压力波的扩散与热传导过程中的温度扩散相似,如果假设裂缝中的压力在注入过程中保持恒定,那么裂缝闭合后的压力递减行为与热衰减行为一致,表示为井底压力pw与线性流时间函数FL的关系式,如下
当t≥tc时
| $ {p_{\rm{w}}}(t)-{p_{\rm{r}}} = {C_{\rm{T}}}\sqrt {\frac{{\pi \mu }}{{K\phi {c_{\rm{t}}}}}} {F_{\rm{L}}}(t, {t_{\rm{c}}}) $ | (4) |
其中
| $ {F_{\rm{L}}}(t,{t_{\rm{c}}}) = \frac{2}{\pi }\arcsin \sqrt {\frac{{{t_{\rm{c}}}}}{t}} $ | (5) |
Horner压降模型将油井晚期径向流动下的压力降描述为Horner时间
| $ {p_{\rm{w}}}(t)-{p_{\rm{r}}} = \frac{{2.51 \times {{10}^5}{V_i}\mu }}{{Kh{t_{\rm{c}}}}}{F_{\rm{R}}}(t, {t_{\rm{c}}}) $ | (6) |
其中
| $ {F_{\rm{R}}}(t, {t_{\rm{c}}}) = \frac{1}{4}\ln \left( {1 + \frac{{\chi {t_{\rm{c}}}}}{{t-{t_{\rm{c}}}}}} \right) \cong \frac{1}{4}\ln \left( {1 + \frac{{1.62{t_{\rm{c}}}}}{{t-{t_{\rm{c}}}}}} \right) $ | (7) |
测试压裂施工停泵后,压裂液在地下裂缝和储层将依次经历以下4个流动时期。
2.1 裂缝延伸期井底压力递减,但仍高于闭合压力,裂缝沿缝长方向延伸,缝宽保持不变。压裂液沿着垂直裂缝壁面的方向线性地滤失到地层中,如图 2a所示。
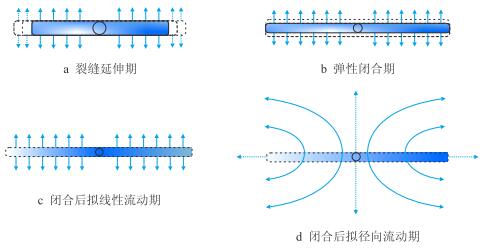 |
| 图2 停泵后地层压裂液流态示意图 Fig. 2 Flow regimes of fracturing fluid after well shut-in |
井底压力递减到延伸压力之后,裂缝停止延伸,转而进入弹性闭合阶段。此阶段裂缝长度保持不变,裂缝壁面的滤失继续进行,缝宽减小,如图 2b所示。直到井底压力递减到闭合压力,裂缝完全闭合,滤失停止,缝宽不再降低。
2.3 闭合后的拟线性流动期闭合时刻滤失到地层的液体以线性的方式向地层扩散,如图 2c所示。整个过程类似于热力学的扩散过程。
2.4 闭合后的拟径向流动期储层中的流体流动到一定程度,开始呈现类似于无限大地层径向流的反向过程,流体以径向流的方式向整个地层扩散,如图 2d所示。
通过对停泵后的井底压力进行数值模拟,得到压降及其导数对停泵时间的双对数曲线,如图 3所示。由红色圆点状的压降导数曲线可以依次识别出斜率为1/2,3/2,1/2和0的4个直线段,分别对应以上描述的裂缝延伸期、弹性闭合期、闭合后的拟线性流和拟径向流动期。
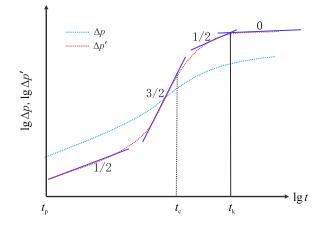 |
| 图3 测试压裂压降及其导数双对数曲线 Fig. 3 Diagnostic pressure drop and its derivative log-log plot |
由闭合期的压降方程可知,在此阶段将压降导数对时间在双对数坐标下会呈现3/2斜率的直线段。当压降偏离此控制方程,视为裂缝完全闭合,因此在偏离3/2斜率的拐点处对应的时间为闭合时间tc,对应的压降∆p(tc)可用来计算闭合压力
| $ {p_{\rm{c}}} = {p_{{\rm{ISI}}}}-\Delta p({t_{\rm{c}}}) $ | (8) |
由闭合后拟线性流动阶段的压降方程可知,在此阶段将井底压力对时间函数FL在直角坐标下会呈现斜率为mL的直线段
| $ {m_{\rm{L}}} = {C_{\rm{T}}}\sqrt {\frac{{\pi \mu }}{{K\phi {c_{\rm{t}}}}}} $ | (9) |
因此,由式(9)可以计算出综合滤失系数CT。
3.3 地层系数Kh的求取由闭合后拟径向流动阶段的压降方程可知,在此阶段将井底压力对时间函数FR在直角坐标下会呈现斜率为mR的直线段
| $ Kh = 251000\frac{{\mu {V_i}}}{{{m_{\rm{R}}}{t_{\rm{c}}}}} $ | (10) |
因此,由式(10)可以计算出地层系数Kh。
3.4 地层压力pr的求取由闭合后拟径向流动阶段的压降方程可知,当FR(t, tc)=0时,pw=pr,此时井底压力对时间函数的曲线与Y轴的截距则为地层压力pr。
4 实例分析 4.1 基本地质特征A井所在区域构造位置位于东海陆架盆地浙东拗陷西湖凹陷中央反转构造带南部,是春晓气田群的一部分。储层岩性以细砂岩为主,储层结构成熟度较高,分选较好,磨圆度以次圆为主,长石风化程度中等。储层流体以干气为主,凝析油含量低。由测井及岩芯实验获得地层基本数据如表 1所示。
| 表1 A井地层及流体性质 Table 1 Properties of formation and fluid for Well A |
A为该区域内完钻的一口开发井,完钻井深为4 100 m,射孔井段为3 980~4 000 m。为了提高单井产量,需对A井进行水力压裂增产改造。于2010-09-16进行小型测试压裂,测试压裂施工共泵注瓜胶压裂液30.7 m3,停泵后关井近16 h。井下压力监测设备获得了整个施工和停泵关井过程中的压力数据,如图 4所示。
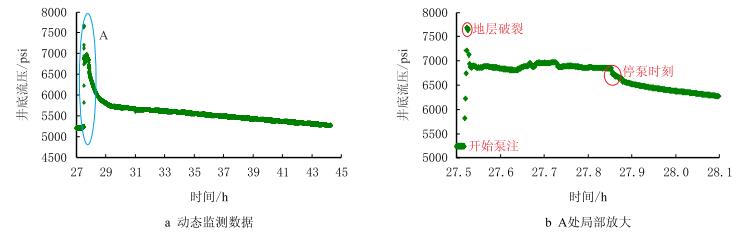 |
| 图4 井下压力动态监测数据 Fig. 4 Downhole pressure monitoring data |
图 4中红色圈出部分显示,地层破裂压力为7 650 psi,瞬时停泵压力为6 579 psi。图 5为测试压裂压降阶段的双对数诊断曲线,压降导数曲线明显反映了4个流动阶段,即:(1)停泵后的裂缝延伸期;(2)裂缝弹性闭合期,压降导数表现为接近于3/2的斜率段;(3)裂缝闭合后的拟线性流动阶段,压降导数表现为1/2斜率的直线段;(4)裂缝闭合后的拟径向流动阶段,压降导数表现为0斜率的直线段。拟径向流后期导数曲线出现了“凹子”阶段,这种现象是由于井筒对流入井底压裂液的储集,被称为“晚期井筒储集”效应。弹性闭合期的最后一个时间点表示裂缝闭合完毕,图 5压降导数曲线偏离3/2斜率的时间点对应的压降值为276 psi,由公式(8)可以计算闭合压力pc为6 303 psi。
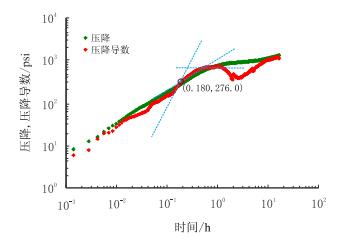 |
| 图5 测试压裂压降双对数诊断曲线 Fig. 5 Pressure drop and its derivative on log-log plot |
图 6为裂缝闭合后期拟径向流动阶段分析曲线,此阶段井底压力在FR时间函数曲线上的斜率mR为397.1,由公式(10)计算出地层系数Kh为254.2 mD·ft(1 ft=0.304 8 m)。给定储层厚度30 m,可计算地层渗透率K为2.56 mD。将斜率mR的直线外推到时间零点,与Y轴截距即为初始地层压力,pr为5 410 psi。图 7为裂缝闭合后期拟线性流动阶段分析曲线,此阶段井底压力在FL时间函数曲线上的斜率mL为144.1,由公式(9)计算出压裂液综合滤失系数CT为2.63×10−4ft·min−1/2。
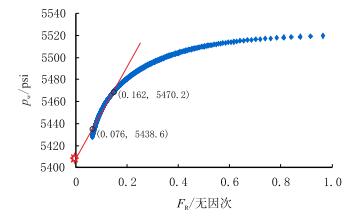 |
| 图6 裂缝闭合后FR函数曲线 Fig. 6 FR function plot after fracture closure |
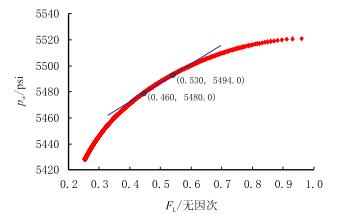 |
| 图7 裂缝闭合后FL函数曲线 Fig. 7 FL function plot after fracture closure |
根据测试压裂施工阶段的井下压力监测数据,连续分析了停泵后各压降段曲线,计算得到了储层物性参数,如表 2所示。结果显示A井所处地层初试压力和破裂压力均正常,预计主压裂施工难度不大;储层渗透率值较低,属于低渗气层,预计主压裂施工压裂液会有较低的滤失值。另外,双对数诊断曲线(图 5)显示压力导数在闭合点之前呈现出多个3/2斜率段,表明水力裂缝具有多个弹性闭合段,怀疑储层发育微裂缝,这将致使主压裂过程中前置液阶段造缝不好,裂缝在储层中延伸受限。
| 表2 A井关键参数确定表 Table 2 Key parameters estimated for Well A |
测试压裂结束后,A井进行了主压裂施工,由主压裂施工净压力拟合方法获得的储层渗透率为2.45 mD,闭合压力为6 178 psi,综合滤失系数为2.92 ×10−4ft·min−1/2,其结果与表 2所列出的相应参数值在5%误差范围内,这验证了本文提出方法的可靠性。
5 结论(1) 测试压裂施工停泵后,压裂液在地下裂缝和储层将依次经历:裂缝延伸、弹性闭合、闭合后的拟线性流和拟径向流4个流动时期。通过对停泵后的井底压力进行数值模拟发现在双对数曲线上,压降导数在上述各个流动期会依次呈现出1/2斜率、3/2斜率、1/2斜率和0斜率段。
(2) 提出了一套“先诊断,再分析”的压力递减分析方法。该方法利用井底压降及其导数的双对数曲线诊断出施工停泵后的各个流动阶段,再分别利用G函数、FL函数和FR函数曲线分析获得压裂储层的关键参数。其中,通过弹性闭合期的G函数分析获得储层闭合压力,通过闭合后拟线性流动期的FL函数分析获得压裂液综合滤失系数,通过闭合后拟径向流动期的FR函数分析获得初始地层压力和渗透率。
(3) 通过对东海低渗气田某测试压裂井的实例应用,证明提出方法操作简便,获取到与裂缝有关的地层物性参数,为制定主压裂设计与指导施工提供了依据。
| [1] | 王鸿勋, 张士诚. 水力压裂数值计算方法[M]. 北京: 石油工业出版社, 1998 : 14 -26. |
| [2] | 张士诚, 张劲. 压裂开发理论与应用[M]. 北京: 石油工业出版社, 2003 : 1 -6. |
| [3] |
赵金洲, 任岚, 胡永全, 等. 裂缝性地层水力裂缝非平面延伸模拟[J].
西南石油大学学报:自然科学版, 2012, 34 (4) : 174 –180.
Zhao Jinzhou, Ren Lan, Hu Yongquan, et al. Numerical simulation on non-planar propagation of hydraulic fracture in naturally fractured formations[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (4) : 174 –180. |
| [4] |
李丹琼, 张士诚, 张遂安. 煤层气井牛顿流体压裂压力损失预测模型[J].
煤田地质与勘探, 2013, 41 (4) : 22 –30.
Li Danqiong, Zhang Shicheng, Zhang Sui'an. Pressure loss prediction model of Newtonian fluid hydraulic fracturing in coalbed methane well[J]. Coal Geology & Exploration, 2013, 41 (4) : 22 –30. |
| [5] | Nolte K G. Determination of fracture parameters from fracturing pressure decline[C]. SPE 8341, 1979. |
| [6] | Mayerhofer M J, Ehligeconomides C A, Economides M J. Pressure-transient analysis of fracture-calibration tests[J]. Journal of Petroleum Technology, 1995, 47 (3) : 229 –234. DOI:10.2118/26527-PA |
| [7] |
王达, 刘刚芝, 冯浦涌, 等. 新型小型压裂摩阻测试方法的应用[J].
新疆石油地质, 2011, 32 (6) : 672 –674.
Wang Da, Liu Gangzhi, Feng Puyong, et al. Application of new mini-rac friction pressure testing technique to gas wells[J]. Xinjiang Petroleum Geology, 2011, 32 (6) : 672 –674. |
| [8] |
徐刚, 彭苏萍, 邓绪彪. 煤层气井水力压裂压力曲线分析模型及应用[J].
中国矿业大学学报, 2011, 40 (2) : 173 –178.
Xu Gang, Peng Suping, Deng Xubiao. Hydraulic fracturing pressure curve analysis and its application to coalbed methane wells[J]. Journal of China University of Mining & Technology, 2011, 40 (2) : 173 –178. |
| [9] |
梁冲, 尚会昌, 卢拥军, 等. 压前测试评价在异常高压致密气藏应用研究[J].
西南石油大学学报:自然科学版, 2011, 33 (1) : 95 –101.
Liang Chong, Shang Huichang, Lu Yongjun, et al. Application and research of per-frac testing technology in abnormal high pressure tight gas reservoir[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (1) : 95 –101. |
| [10] |
李亭. 煤层气井小型测试压裂优化设计研究[J].
天然气勘探与开发, 2013, 36 (4) : 74 –76.
Li Ting. Optimal design of small-scale test fracturing for CBM wells[J]. Natural Gas Exploration & Development, 2013, 36 (4) : 74 –76. |
| [11] |
曲冠政, 曲占庆, 岳艳如. 压裂施工曲线诊断方法[J].
科学技术与工程, 2013, 13 (5) : 1281 –1284, 1288.
Qu Guanzheng, Qu Zhanqing, Yue Yanru. The diagnosis method of fracturing curve[J]. Science Technology and Engineering, 2013, 13 (5) : 1281 –1284, 1288. |
| [12] | Mohamed I M, Azmy R M, Sayed M A I, et al. Evaluation of after-closure analysis techniques for tight and shale gas formations[C]. SPE 140136, 2011. |
| [13] | Nolte K G, Maniere J L, Owens K A. After-closure analysis of fracture calibration tests[C]. SPE 38676, 1997. |
| [14] | Talley G R, Swindell T M, Waters G A, et al. Field application of after-closure analysis of fracture calibration tests[C]. SPE 52220, 1999. |
| [15] | Wang F. Processing and analysis of transient pressure measurements from permanent down-hole gauges[J]. Petroleum Science, 2012, 9 (3) : 330 –335. DOI:10.1007/s12182-012-0216-7 |
| [16] | Wang Fei. Pressure transient analysis of multi-stage hydraulically fractured horizontal wells[J]. Journal of Petroleum Science Research, 2013, 2 (4) : 162 –166. DOI:10.14355/jpsr.2013.0204.03 |
 2014, Vol. 36
2014, Vol. 36

