双台阶水平井作为一种特殊的水平井井型,日益得到广泛应用[1]。国外还未有人专门针对双台阶水平井渗流规律和产能评价作过研究[2]。国内仅有少数关于双台阶水平井产能评价的研究[3-4],目前对考虑井筒压降损失的双台阶水平井不稳定渗流的研究是一片空白。
本文以双台阶水平井油藏不稳定渗流模型为基础,与井筒内变质量流动压降损失模型进行耦合,建立了双台阶水平井不稳定渗流耦合模型,并给出了定压生产条件下模型解法和实例。
1 双台阶水平井不稳定渗流模型将双台阶水平井进行空间离散,分段示意图见图 1。
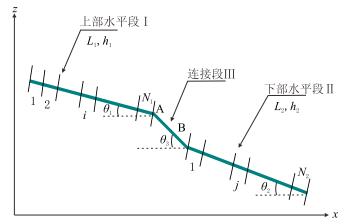 |
| 图1 任意位置双台阶水平井xoz平面投影及分段示意图 Fig. 1 Arbitrary two-stepped horizontal well proj |
并对模型做以下基本假设:(1)薄层油藏为均质、各向同性地层;(2)油层上、下边界封闭,水平无限大;(3)水平段均采用裸眼完井方式,且连接段Ⅲ对产能没有贡献。
以上下边界封闭、水平无限大油藏中水平井不稳定渗流模型[5-6]为基础,根据势叠加原理,得到薄互层油藏中双台阶水平井不稳定渗流关系式,为(N1+N2)阶方程组[7]
| $ Aq = P $ | (1) |
其中
| $ A = \left[{\begin{array}{*{20}{c}} {{F_{{\rm{up}}1, 1}}}& \cdots &{{F_{{\rm{up}}1, {N_1}}}}&0& \cdots &0\\ {{F_{{\rm{up}}2, 1}}}& \cdots &{{F_{{\rm{up}}2, {N_1}}}}&0& \cdots &0\\ \vdots &{}& \vdots & \vdots &{}& \vdots \\ {{F_{{\rm{up}}{N_1}, 1}}}& \cdots &{{F_{{\rm{up}}{N_1}, {N_1}}}}&0& \cdots &0\\ 0& \cdots &0&{{F_{{\rm{dn}}1, 1}}}& \cdots &{{F_{{\rm{dn}}1, {N_2}}}}\\ 0& \cdots &0&{{F_{{\rm{dn}}2, 1}}}& \cdots &{{F_{{\rm{dn}}2, {N_2}}}}\\ \vdots &{}& \vdots & \vdots &{}& \vdots \\ 0& \cdots &0&{{F_{{\rm{dn}}{N_2}, 1}}}& \cdots &{{F_{{\rm{dn}}{N_2}, {N_2}}}} \end{array}} \right] $ |
| $ q = \left[{\begin{array}{*{20}{c}} {{q_{{\rm{upr}}1}}}\\ {{q_{{\rm{upr}}2}}}\\ \vdots \\ {{q_{{\rm{upr}}{N_1}}}}\\ {{q_{{\rm{dnr}}1}}}\\ {{q_{{\rm{dnr}}2}}}\\ \vdots \\ {{q_{{\rm{dnr}}{N_2}}}} \end{array}} \right], P = \left[{\begin{array}{*{20}{c}} {\Delta {p_{{\rm{upwf}}1}}}\\ {\Delta {p_{{\rm{upwf}}2}}}\\ \vdots \\ {\Delta {p_{{\rm{upwf}}{N_1}}}}\\ {\Delta {p_{{\rm{dnwf}}1}}}\\ {\Delta {p_{{\rm{dnwf}}2}}}\\ \vdots \\ {\Delta {p_{{\rm{dnwf}}{N_2}}}} \end{array}} \right] $ |
| $ \begin{array}{*{20}{l}} {{{\overline {{F_{{\rm{up}}}}} }_{i, j}} = \frac{\mu }{{\pi k({L_1}/{N_1})}}\int_{{x_{{\rm{upwD}}j1}}}^{{x_{{\rm{upwD}}j2}}} {\frac{1}{s} \cdot M\left[{\zeta, {y_{{\rm{wD}}}}(\zeta ), {z_{{\rm{wD}}}}(\zeta )} \right]} \cdot }\\ {\frac{{\sqrt {{{({x_{{\rm{upwD}}j1}} -{x_{{\rm{upwD}}j2}})}^2} + {{({y_{{\rm{upwD}}j1}} -{y_{{\rm{upwD}}j2}})}^2} + {{({z_{{\rm{upwD}}j1}} -{z_{{\rm{upwD}}j2}})}^2}} }}{{{x_{{\rm{upwD}}j2}} - {x_{{\rm{upwD}}j1}}}}{\rm{d}}\zeta } \end{array} $ |
| $ \begin{array}{*{20}{l}} {{{\overline {{F_{{\rm{dn}}}}} }_{i, j}} = \frac{\mu }{{\pi k({L_2}/{N_2})}}\int_{{x_{{\rm{dnwD}}j1}}}^{{x_{{\rm{dnwD}}j2}}} {\frac{1}{s} \cdot M\left[{\zeta, {y_{{\rm{wD}}}}(\zeta ), {z_{{\rm{wD}}}}(\zeta )} \right]} \cdot }\\ {\frac{{\sqrt {{{({x_{{\rm{dnwD}}j1}} -{x_{{\rm{dnwD}}j2}})}^2} + {{({y_{{\rm{dnwD}}j1}} -{y_{{\rm{dnwD}}j2}})}^2} + {{({z_{{\rm{dnwD}}j1}} -{z_{{\rm{dnwD}}j2}})}^2}} }}{{{x_{{\rm{dnwD}}j2}} - {x_{{\rm{dnwD}}j1}}}}{\rm{d}}\zeta } \end{array} $ |
| $ M\left[{\zeta, {y_{{\rm{wD}}}}(\zeta ), {z_{{\rm{wD}}}}(\zeta )} \right] = {K_0}\left[{{r_{{\rm{up}}j{\rm{D}}}}(\zeta )\sqrt s } \right] \\+ 2\sum\limits_{n = 1}^{NT} {{K_0}\left[{{r_{{\rm{up}}j{\rm{D}}}}(\zeta ){\varepsilon _n}} \right]\cos (n\pi \frac{{{z_{\rm{D}}}}}{{{h_{{\rm{1D}}}}}})\cos [n\pi \frac{{{z_{{\rm{wD}}}}(\zeta )}}{{{h_{{\rm{1D}}}}}}]} $ |
| $ {r_{{\rm{up}}j{\rm{D}}}}(\zeta ) = \sqrt {{{\left( {\zeta- {x_{\rm{D}}}} \right)}^2} + {{\left\{ {\left[{\frac{{{y_{{\rm{upwD}}j1}}-{y_{{\rm{upwD}}j2}}}}{{{x_{{\rm{upwD}}j1}}-{x_{{\rm{upwD}}j2}}}}\left( {\zeta-{x_{{\rm{upwD}}j1}}} \right) + {y_{{\rm{upwD}}j1}}} \right] -{y_{\rm{D}}}} \right\}}^2}} $ |
拉普拉斯空间
对于上部水平段,取任意微元段进行分析。如图 2所示。设:
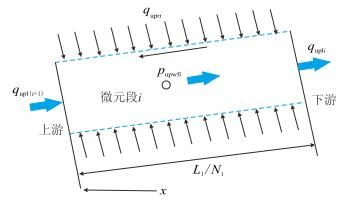 |
| 图2 上部水平段第i微元段井筒流体流动示意图 Fig. 2 The diagram of fluid flowing in the ith element section of the upper horizontal segment |
各微元段轴向流量为:qupl1,qupl2,…,quplN1;
各微元段的单位长度径向流量为:qupr1,qupr2,…,quprN1;
各微元段的井筒流压为:pupwf1,pupwf2,…,pupwfN1;
第i微元段上游端的轴向流量为qupli1,下游端的轴向流量为qupli2
根据质量守恒定理和动量定理得到上部生产段第i段的井筒压力损失[9-11]为
| $ \Delta {p_{{\rm{upseg}}}}(i) = \frac{{2f\rho }}{{{\pi ^2}{D^5}}}{\left( {2{q_{{\rm{upl}}i1}} + {q_{{\rm{upr}}i}} \cdot \frac{{{L_1}}}{{{N_1}}}} \right)^2}\frac{{{L_1}}}{{{N_1}}} \\+ \frac{{16\rho {q_{{\rm{upr}}i}}}}{{{\pi ^2}{D^4}}}\frac{{{L_1}}}{{{N_1}}}\left( {2{q_{{\rm{upl}}i1}} + {q_{{\rm{upr}}i}} \cdot \frac{{{L_1}}}{{{N_1}}}} \right) + \frac{{{L_1}}}{{{N_1}}}\rho {\rm{g}}\sin {\theta _1} $ | (2) |
| $ \begin{array}{l} {q_{{\rm{upl}}i1}} = \frac{{{L_1}}}{{{N_1}}}\sum\limits_{k = i + 1}^{{N_1}} {{q_{{\rm{upr}}k}}} + \frac{{{L_2}}}{{{N_2}}}\sum\limits_{j = 1}^{{N_2}} {{q_{{\rm{dnr}}j}}}, \\ i = 1{\rm{, }}2{\rm{, }} \ldots {\rm{, }}{N_1}-1 \end{array} $ | (3) |
| $ {q_{{\rm{upl}}{N_1}1}} = \frac{{{L_2}}}{{{N_2}}}\sum\limits_{j = 1}^{{N_2}} {{q_{{\rm{dnr}}j}}} $ | (4) |
上部水平段第1段下游端的轴向流量即为井筒总流量为
| $ Q = {q_{{\rm{upl}}12}} = \frac{{{L_1}}}{{{N_1}}}\sum\limits_{k = 1}^{{N_1}} {{q_{{\rm{upr}}k}}} + \frac{{{L_2}}}{{{N_2}}}\sum\limits_{j = 1}^{{N_2}} {{q_{{\rm{dnr}}j}}} $ | (5) |
同理,可以得到下部水平段Ⅱ第j微元段井筒压降损失计算模型
| $ \Delta {p_{{\rm{dnseg}}}}(j) = \frac{{2f\rho }}{{{\pi ^2}{D^5}}}{\left( {2{q_{{\rm{dnl}}j1}} + {q_{{\rm{dnr}}j}} \cdot \frac{{{L_2}}}{{{N_2}}}} \right)^2}\frac{{{L_2}}}{{{N_2}}} \\+ \frac{{16\rho {q_{{\rm{dnr}}j}}}}{{{\pi ^2}{D^4}}}\frac{{{L_2}}}{{{N_2}}}\left( {2{q_{{\rm{dnl}}j1}} + {q_{{\rm{dnr}}j}} \cdot \frac{{{L_2}}}{{{N_2}}}} \right) + \frac{{{L_2}}}{{{N_2}}}\rho {\rm{g}}\sin {\theta _2} $ | (6) |
| $ {q_{{\rm{dnl}}j1}} = \frac{{{L_2}}}{{{N_2}}}\sum\limits_{k = j + 1}^{{N_2}} {{q_{{\rm{dnr}}k}}} {\rm{, }}j = 1{\rm{, }}2{\rm{, }} \ldots {\rm{, }}{N_2}-1 $ | (7) |
下部生产段第1段下游端轴向流量为
| $ {q_{{\rm{dnl}}12}} = \frac{{{L_2}}}{{{N_2}}}\sum\limits_{k = 1}^{{N_2}} {{q_{{\rm{dnr}}k}}} $ | (8) |
下部生产段趾端流量为0,即:qdnlN21=0
对于连接段Ⅲ仅考虑该段沿程压降损失,径向流入该段井筒的流量为0,可认为连接段内流体的流速大小保持不变,在两端的弯道处只改变了流体的流速方向。则该段的压降计算模型为
| $ \Delta {p_{{\rm{midseg}}}} = \frac{{8{f_0}\rho Q_{{\rm{dn}}}^2{L_3}}}{{{\pi ^2}{D^5}}} + \rho {\rm{g}}{L_3}\sin {\theta _3} $ | (9) |
| $ {Q_{{\rm{dn}}}} = {q_{{\rm{dnl12}}}} $ | (10) |
采用Chen公式(任意Re,任意ε/D值)计算f0
| $ \frac{1}{{\sqrt {{f_0}} }} =-2\log \left( {\frac{\varepsilon }{{3.7065D}}-5.0452\frac{A}{{Re}}} \right) $ | (11) |
| $ A = \log \left[{\frac{{{{\left( {\varepsilon /D} \right)}^{1.1098}}}}{{2.8257}} + \frac{{5.8506}}{{R{e^{0.8981}}}}} \right] $ | (12) |
其中:
| $ Re = \frac{{\rho vD}}{\mu } $ | (13) |
对于裸眼完井情况,存在壁面径向流入时,采用Liang-Biao Ouyang给出层流时的计算公式[12]
| $ f = {f_0}(1 + 0.04304Re_{\rm{w}}^{0.6142}) $ | (14) |
紊流条件下计算公式为
| $ f = {f_0}\left[{1-29.03{{\left( {\frac{{R{e_{\rm{w}}}}}{{Re}}} \right)}^{0.8003}}} \right] $ | (15) |
| $ R{e_{\rm{w}}} = \frac{{{q_{\rm{I}}}\rho }}{{\pi \mu }} $ | (16) |
设双台阶水平井跟端流压为pwf,则生产段各微元段井筒流压之间的关系为
上部水平段
| $ \begin{array}{l} {p_{{\rm{upwf}}i}} = {p_{{\rm{upwf}}(i-1)}} + \frac{{\Delta {p_{{\rm{upseg}}}}(i) + \Delta {p_{{\rm{upseg}}}}(i-1)}}{2}, \\ i = 2{\rm{, }}3 \ldots {N_1} \end{array} $ | (17) |
| $ {p_{{\rm{upwf}}1}} = {p_{{\rm{wf}}}} + \frac{1}{2}\Delta {p_{{\rm{upseg}}}}(1) $ | (18) |
连接段Ⅲ
上端点A(与上部生产段的交点)
| $ {p_{{\rm{mid}}2}} = {p_{{\rm{upwf}}{N_1}}} + \frac{{\Delta {p_{{\rm{upseg}}}}({N_1})}}{2} $ | (19) |
下端点B(与下部生产段的交点)
| $ {p_{{\rm{mid}}1}} = {p_{{\rm{mid}}2}} + \Delta {p_{{\rm{midseg}}}} $ | (20) |
下部水平段
| $ {p_{{\rm{dnwf}}i}} = {p_{{\rm{dnwf}}(i-1)}} + \frac{{\Delta {p_{{\rm{dnseg}}}}(i) + \Delta {p_{{\rm{dnseg}}}}(i-1)}}{2}, i = 2{\rm{, }}3{\rm{, }} \ldots {\rm{, }}{N_1} $ | (21) |
| $ {p_{{\rm{dnwf}}1}} = {p_{{\rm{mid}}1}} + \frac{{\Delta {p_{{\rm{dnseg}}}}(1)}}{2} $ | (22) |
| $ {p_{\rm{toe}}} = {p_{{\rm{dnwf}}{N_2}}} + \dfrac{{\Delta {p_{\rm{dnseg}}}({N_2})}}{2} $ | (23) |
将式(2)、式(6)、式(9)代入式(17)~(23)中得到(N1+N2)个关于未知量pupwfi、pdnwfj、qupri和qdnrj的双台阶水平井各微元段径向流入与流压之间的连接方程
| $ F({p_{{\rm{upwf}}i}}, {p_{{\rm{dnwf}}j}}, {q_{{\rm{upr}}i}}, {q_{{\rm{dnr}}j}}) = 0 $ | (24) |
建立的双台阶水平井不稳定流动耦合模型较为复杂,采用迭代法进行求解。对于定井底流压生产条件,求解步骤如下:
(1) 先给定一组pupwfi和pdnwfj的初值,(已知跟端流压pwf,可将pupwfi和pdnwfj的初值给定为pwf),采用式(1)计算得到qupri和qdnrj;
(2) 然后再将其代入井筒压降计算模型式(2)~式(10),计算每段井筒的压降损失;
(3) 计算方程(1)的右边项(即每段的生产压差);
(4) 代入式(1),重新计算得到pupwfi和pdnwfj,由此完成一次迭代;
(5) 再将新得到的pupwfi和pdnwfj值作为新初值,重复上述过程进行计算,直到前后两次迭代计算误差小于允许误差为止。
| $ \Delta {p_{{\rm{upwf}}i}} = {p_{{\rm{in}}i}}- \left[{{p_{{\rm{wf}}}} + \sum\limits_{k = 1}^i {\Delta {p_{{\rm{upseg}}}}(k)-\frac{{\Delta {p_{{\rm{upseg}}}}(i)}}{2}} } \right]{\rm{, }}i = 1{\rm{, }} \ldots \ldots {\rm{, }}{N_1} $ | (25) |
| $ \begin{array}{l} \Delta {p_{{\rm{dnwf}}j}} = {p_{{\rm{in}}i}}- \left[{{p_{{\rm{wf}}}} + \sum\limits_{k = 1}^{{N_1}} {\Delta {p_{{\rm{upseg}}}}(k) + \Delta {p_{{\rm{midseg}}}} + \sum\limits_{k = 1}^j {\Delta {p_{{\rm{dnseg}}}}(j)}-\frac{{\Delta {p_{{\rm{dnseg}}}}(j)}}{2}} } \right]{\rm{, }}\\ j = 1{\rm{, }} \ldots \ldots {\rm{, }}{N_2} \end{array} $ | (26) |
一口阶梯水平井的地层参数和钻完井数据见表 1,原油密度870 kg/m3,原油黏度0.01 Pa·s,油藏渗透率2 D,原始地层压力13.1 MPa,水平井眼直径0.1 m,井斜角均为90°,定井底压力生产,pheel=11.6 MPa。应用建立的双台阶水平井不稳定渗流耦合模型进行计算。计算结果见图 3~图 5。
| 表1 双台阶水平井产能计算参数 Table 1 Productivity calculation parameters of two-stepped horizontal well |
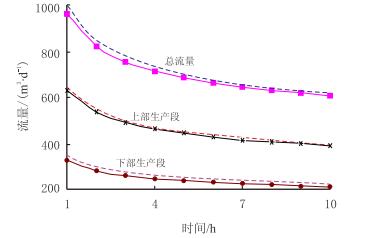 |
| 图3 双台阶水平井流量随时间变化曲线(虚线代表无限导流情况) Fig. 3 The flow versus time curve of the two-stepped horizontal well(dashed line represents the infinite conductivity case) |
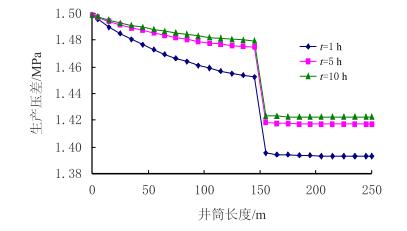 |
| 图4 双台阶水平井上、下生产段沿程生产压差分布图 Fig. 4 Drawdown pressure distribution along the upper and lower segments of two-stepped horizontal well |
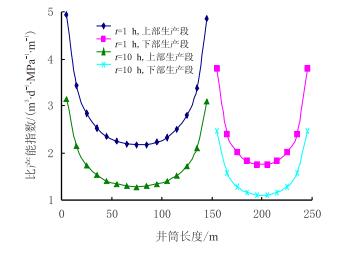 |
| 图5 双台阶水平段比采油指数沿程分布图 Fig. 5 Productivity index distribution along the wellbore of the two-stepped horizontal well |
图 3对比了无限导流情况下和考虑井筒压降下的井筒流量随时间的变化。可以看出:流量随时间的增加而减少;无限导流情况下的流量大于有限导流情况下的流量,两者的差值随时间增大而减小。
图 4给出了不同时刻上、下生产段沿程生产压差的变化曲线。可以看出:连接段损失的压力较大,随时间增大而减小,大约为0.055 8 MPa,占整个井筒内压降损失的一半以上;随时间增加,井筒内压降损失减小,从0.105 5 MPa(占地层压降的7.04%)减小到0.076 1 MPa(占地层压降损失的5.08%);上、下部生产段靠近趾端的压力梯度较小,沿流动方向,压力梯度增大;连接段处压力梯度最大;整体上,上部生产段的压力梯度大于下部生产段的压力梯度。因此,对高渗透层,井筒内压降损失可使产量明显减少,特别是在生产初期,对产能的影响更为明显,可适当增加井筒直径,减小压降损失,提高产量。
从图 5可以看出:由于本文所建立的模型考虑了井筒内压降损失以及上、下生产段各微元段生产时相互之间的干扰,导致比产能指数沿井筒长度不是均匀分布的,大致呈“ U”型分布,非对称,跟端的比产能指数略高于趾端;随时间增大,比产能指数降低。
6 结论(1) 应用质量守恒定理和动量定理建立了薄互层油藏中双台阶水平井井筒沿程压降计算模型。
(2) 推导了双台阶水平井不稳定渗流与井筒内变质量流动耦合的数学模型,给出了定压生产条件下模型解法,并进行了应用计算。
(3) 比产能指数沿井筒长度不是均匀分布的,大致呈非对称“ U”型分布,且跟端的比产能指数略高于趾端。
(4) 井筒沿程压差分布曲线明显有一个台阶,说明压降损失主要集中在中间夹层连接段处,主要为重力压降损失;因此,建议设计和钻进双台阶水平井时应使水平段尽量水平,连接段平缓,以减少重力压降对产量的影响。
| [1] |
荣宁, 吴迪, 韩易龙, 等. 双台阶水平井在塔里木盆地超深超薄边际油藏开发中的应用及效果评价[J].
天然气地球科学, 2006, 17 (2) : 230 –232.
Rong Ning, Wu Di, Han Yilong, et al. The application and effectiveness evaluation of double-step horizontal wells in super-deep and super-thin margin reservoir of Tarim[J]. Natural Gas Geoscience, 2006, 17 (2) : 230 –232. |
| [2] |
韩国庆, 吴晓东, 李相方, 等. 国外非常规井模型研究进展[J].
石油钻采工艺, 2004, 26 (1) : 47 –51.
Han Guoqing, Wu Xiaodong, Li Xiangfang, et al. Summary of present studies on modeling of non-conventional wells[J]. Oil Drilling & Production Technology, 2004, 26 (1) : 47 –51. |
| [3] |
黄世军, 程林松, 赵凤兰, 等. 阶梯水平井生产段油藏渗流与井筒变质量管流的耦合模型[J].
水动力学研究与进展, 2005, 20 (4) : 463 –471.
Huang Shijun, Cheng Linsong, Zhao Fenglan, et al. The flow model coupling reservoir percolation and variable mass pipe flow in production section of the stepped horizontal well[J]. Journal of Hydrodynamics, 2005, 20 (4) : 463 –471. |
| [4] |
黄世军, 程林松, 赵凤兰, 等. 薄互层油藏中阶梯水平井产能评价模型研究[J].
西南石油大学学报, 2007, 29 (3) : 60 –65.
Huang Shijun, Cheng Linsong, Zhao Fenglan, et al. The productivity evaluationmodel of the stepped horizontal well in thin in-terbeded reservoirs[J]. Journal of Southwest Petroleum Universtiy, 2007, 29 (3) : 60 –65. |
| [5] | Ozkan E, Raghavan R. New solution for well test analysis problems:part 1-analytical considerration[C]. SPE 18615, 1991. |
| [6] | Ozkan E, Raghavan R. New solutions for well-testanalysis problems:part 2-computational considerations and applications[C]. SPE 18616, 1991. |
| [7] | 李苗.水平井、双台阶水平井渗流理论及应用研究[D].成都:西南石油大学, 2010. |
| [8] | 孔祥岩. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 1999 . |
| [9] |
刘想平, 郭呈柱, 蒋志祥, 等. 油层中渗流与水平井筒内流动的耦合模型[J].
石油学报, 1999, 20 (3) : 82 –86.
Liu Xiangping, Guo Chengzhu, Jiang Zhixiang, et al. The model coupling fluid flow in the reservoir with flow in the horizontal wessbore[J]. Acta Petrolei Sinica, 1999, 20 (3) : 82 –86. |
| [10] |
陈要辉, 阎铁, 刘颖, 等. 裸眼完井分支水平井井筒压力分布理论研究[J].
钻采工艺, 2004, 27 (1) : 1 –3.
Chen Yaohui, Yan Tie, Liu Ying, et al. Theoretical researchon the pressure distribution in the wellbore of multilateral horizontal wells with open hole completion[J]. Drilling & Production Technology, 2004, 27 (1) : 1 –3. |
| [11] |
刘想平, 张兆顺, 刘翔鹗, 等. 水平井筒内与渗流耦合的流动压降计算模型[J].
西南石油学院学报, 2000, 22 (2) : 36 –39.
Liu Xiangping, Zhang Zhaoshun, Liu Xiang'e, et al. A model to calculate pressure drops of horizontal wellbore variable massflow coupled with flow in a reservoir[J]. Journal of Southwest Petroleum Institute, 2000, 22 (2) : 36 –39. |
| [12] | 姜振强.水平井管流对产能影响研究[D].北京:中国地质大学(北京), 2006. http://cdmd.cnki.com.cn/article/cdmd-11415-2006060067.htm |
 2014, Vol. 36
2014, Vol. 36

