2. 中国石油集团工程设计有限公司, 北京 海淀 100085
2. China Petroleum Engineering Design Co. Ltd., Haidian, Beijing 100085, China
近年来中国长输油气管道工程蓬勃发展,由于其线状和网状分布特点,不可避免地要通过一些滑坡地质灾害多发区,滑坡所导致的地表变形对管道的安全构成严重危害[1]。地震引发的滑坡是导致埋地管道破坏的重要原因之一,而埋地管道是生命线系统工程的重要组成部分,被广泛应用于输油、供气、供水等系统中,是现代化生产和城镇生活的大动脉,在滑坡等地震灾害作用下,当管道的应力水平超过其承载能力时,管道就会失效而引发泄漏和爆炸,给人民生命财产造成重大损失[2],因此,分析滑坡作用下埋地管道的反应规律是必要的。
近年来,国内外学者提出了多种埋地管道的分析理论和方法[2-19],目前研究最多的是弹性地基梁和土弹簧模型。弹性地基梁主要考虑土体最终位移对管道的作用,是一种静力分析方法,土弹簧模型主要是将土体简化为纵向、横向和轴向的弹性土弹簧,通过土弹簧系数变化模拟不同的土体类型对管道的作用。由于滑坡带的埋地管道受力非常复杂,本文采用有限元法对西部某段滑坡带管道受力和变形进行力学强度分析和研究,为确定安全滑坡带长度提供理论依据。
1 滑坡的理论分析 1.1 理论分析滑坡系指构成斜坡的岩土体在重力作用下失稳,沿着坡体内部的一个(或多个)软弱面(带)发生剪切而产生的整体性下滑现象。滑坡发生一定的地貌、地形、地质、水文和气候条件下,具有不同的规模,涉及范围从几立方米的岩土物质小的下滑到几平方公里的巨大滑动。处于滑坡状态中的管道要受到泥土的下塌力作用,本身与泥土一道下滑。下塌土对管道的作用力有两种,一种是在纵坡上向管道中线方向下塌,在管道中产生压应力、拉应力或两者同时发生的应力,这是较普遍的一种;另一种是土壤垂直于管道中线或与中线成一个角度下塌,这样的土壤作用力最为危险,此时的管道不仅受拉张作用,还要发生弯曲,在一定条件下管道可能破裂[4]。
本文将对较常见的有一定斜坡的滑坡带进行分析,对其应力应变情况进行讨论。土压力的计算是一个非常复杂、影响因素众多的课题,比如挡土墙的刚体位移与墙身自身变形对土压力的影响就很复杂,目前工程中常用的理论模型是郎肯理论模型。郎肯理论模型是一种比较简单的理论模型,对于黏性土和无黏性土都可以计算。其基本原理是:处于任意深度的土的压力强度大小与深度成正比关系,沿挡土墙呈三角形分布[5],根据郎肯理论模型,任意深度处的土应力对埋地管道的侧压力为
| $ {\sigma_{\rm{z}}} = z\gamma {k_0} $ | (1) |
式中:
σz-侧向压力,MPa;
z-计算点距离土面的距离,m;
γ-墙后的土体重度,MPa/m;
k0-土的压力系数,黏土一般取0.5~0.7。
在斜坡泥土同时下滑的滑坡发生时,管道受到的力有管道内压、高压气体的重力(或油品的重力)、管道自身的重力、管道上方土的压力、土对管道上下方的摩擦力以及管道下方土对管道的作用力。理论和实践证明,在滑坡发生时,管道常见的破坏位置通常在滑动体的两端,即管道的潜在危险区可能是在滑动体的两端[6]。分析滑坡过程中管-土的应力情况,建立管-土模型如图 1所示。
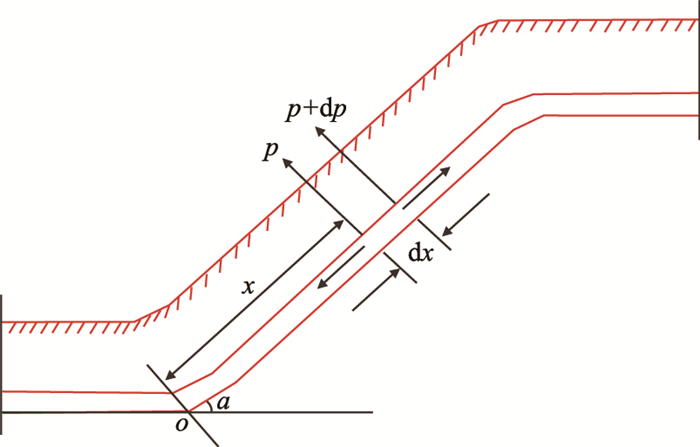 |
| 图1 斜坡管道-土模型示意图 Fig. 1 Schematic diagram of the model of pipeline-soil within slope |
根据弹性力学理论,取图 1中微元dx进行力学分析和推导。根据管道的边界条件,可以推导出埋地管道由于滑坡引起的位移变化沿滑坡管道位置的变化关系为式(6)。
| $ {\rm{ \mathsf{ π} }}\tau D{\rm{d}}x = {\rm{d}}p $ | (2) |
| $ p={\sigma _{\rm{z}}}A $ | (3) |
| $ {\sigma _{\rm{z}}} = \dfrac{{{\rm{d}}u}}{{{\rm{d}}x}}E $ | (4) |
| $ \frac{{{{\rm{d}}^2}u}}{{{{\rm{d}}^2}x}}-\frac{{{\rm{ \mathsf{ π} }}D\tau }}{{EA}} = 0 $ | (5) |
| $ u = \frac{{{\rm{ \mathsf{ π} }}D\tau {x^2}}}{{2E{\rm{A}}}} + {{\rm{C}}_1}x + {{\rm{C}}_2} $ | (6) |
式中:
τ-单位土壤摩擦力,kN/m2;
D-管道外径,mm;
x-管道斜坡段位置,m;
dx-管道斜坡段位置微元段,m;
p-管道中的纵向力,N;
dp-管道中微元段纵向力,N;
A-管道横截面积,m2;
u-管道截面的位移,m;
du-管道截面的微元位移,m;
E-管道弹性模量,MPa;
C1和C2-由边界条件确定的两个常数。
可以根据现实情况对边界条件进行设定,按照理想情况,设定两端不出现位移时,斜坡埋地管道上半端受拉,下半端受压,在管道中端处变形不存在,轴向应力近似为零。实际上,管道的上下两端都将出现位移,斜坡上的管道是上部受拉,下部受压,应力为零处偏移管道中端。
1.2 有限元数值模拟分析埋地管道受力非常复杂,一般的理论研究均需要做大量简化,随着有限元技术的发展,有限元法在计算埋地管道的力学分析方面具有很大的优越性。在考虑滑坡等地面大位移对地下管道的影响时,问题的关键在于怎样考虑土与地下管道之间的相互作用,随着数值方法的发展,管土相互作用问题的研究取得了相当大的进展。前人分别利用ADINA和ANSYS等有限元分析软件,建立了滑坡作用下埋地管道和液化场地中埋地管道的土弹簧分析模型[2-3, 7-19],考虑了管土之间相互作用的非线性特征,得到了管道的受力规律及失效因素。本文用ABAQUS有限元分析软件,建立具有斜坡的滑坡作用下埋地管道的土弹簧分析模型,同时考虑管土材料的非线性以及大变形的几何非线性特征,对埋地管道进行有限元数值模拟分析和研究,为现场设计、施工提供理论依据。
2 埋地管道有限元仿真模拟分析 2.1 管土有限元模型建立本文建立的管土有限元力学模型见图 2,该模型采用软件ABAQUS中提供的一类特殊的单元来模拟埋地管道与土壤的相互作用,单元简称为PSI(Pipe-soil interaction),它可以方便和准确地模拟埋地管道与土壤的相互作用和管道不同工况和不同边界条件下的应力和变形。其力和位移边界条件数据可用式(1)和式(6)计算出。
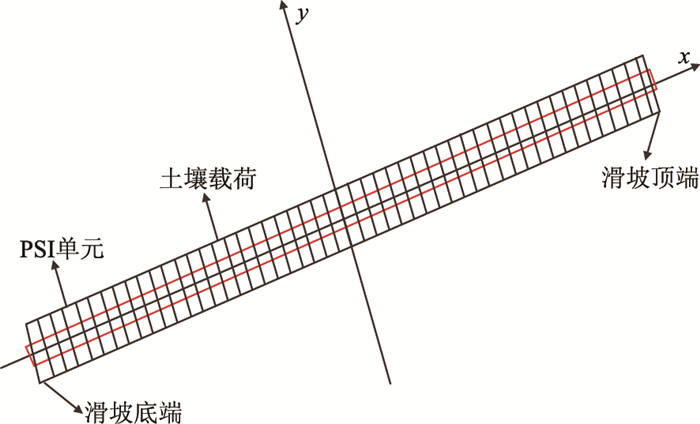 |
| 图2 管土有限元力学模型 Fig. 2 Finite element model of pipeline-soil |
在进行应力计算时,取Von Mises应力σvms(即第四强度理论)进行分析,其计算式见式(7),该应力可以直接判断管道是否发生屈服应力变形和破坏。当Von Mises应力σvms等于或大于管道材料的屈服应力σs时,管道发生屈服变形破坏。
| $ {\sigma _{{\rm{vms}}}} = \sqrt {\frac{{{{({\sigma _1}-{\sigma _2})}^2} + {{({\sigma _1}-{\sigma _3})}^2} + {{({\sigma _3}-{\sigma _2})}^2}}}{2}} $ | (7) |
式中:σvms-Von Mises应力,MPa;σ1,σ2,σ3-管道内任意点的3个主应力,MPa。
2.2 模型基本参数根据西部某管道的实际土壤环境和管道结构情况可知,管道材料为X-80钢管段,弹性模量E=2.034×105 MPa,泊松比为0.30;管道直径D=1 016 mm,壁厚t=17.5 mm,管道埋深h=1.5 m,输送介质为天然气,内压为10 MPa;管道输高压气体重力Gj=962.4 N/m,管道自重Gz=4 223.1 N/m,埋管土壤为黄土,其重度为16.5 kN/m3,则上覆土壤重量Gt=25 146.0 N/m。
管道两旁黄土剥落时给管道上方黄土造成剪切,假设管道两边的黄土理想下滑,土与土间的剪切力为黄土的抗剪强度极限,其基本力学参数为:剪应力τ=2.4 kN/m2,黄土内摩擦角φ=25.40,弹性模量30 MPa,泊松比为0.25。
2.3 仿真结果根据西部某段埋地管道的土坡结构,本文设计了滑坡长度为15.0,20.0和30.0 m,斜坡角度为20°,30°和45°,总共9种埋地管道结构方式,得到不同斜坡角、不同滑坡长度下管道内的最大Von Mises应力数值如表 1所示。
| 表1 不同滑坡情况下管道的Von Mises应力 Table 1 Von Mises stresses of pipeline under different landslips |
从表 1中可以看出:(1)在斜坡角度相同的情况下,管道的最大Von Mises应力随着滑坡长度的增加而增大;(2)在滑坡长度一定的情况下,管道内的最大Von Mises应力随着斜坡角度的增加而增大。
以滑坡长度为15.0 m的情况为例进行详细分析,其结果见图 3和图 4,图 3是管道的Von Mises应力随滑坡长度变化的关系曲线,图 4是管道应变随滑坡长度变化的关系曲线。
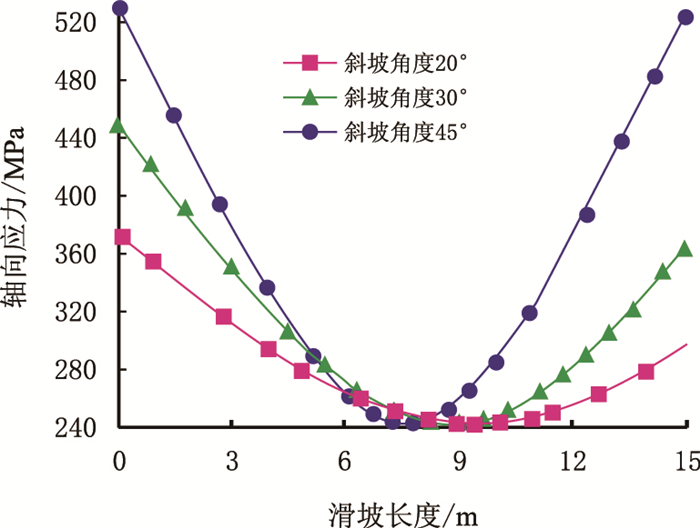 |
| 图3 管道的Von Mises应力随滑坡长度变化 Fig. 3 Curves of pipeline Von Mises stresses varied with the length of landslips |
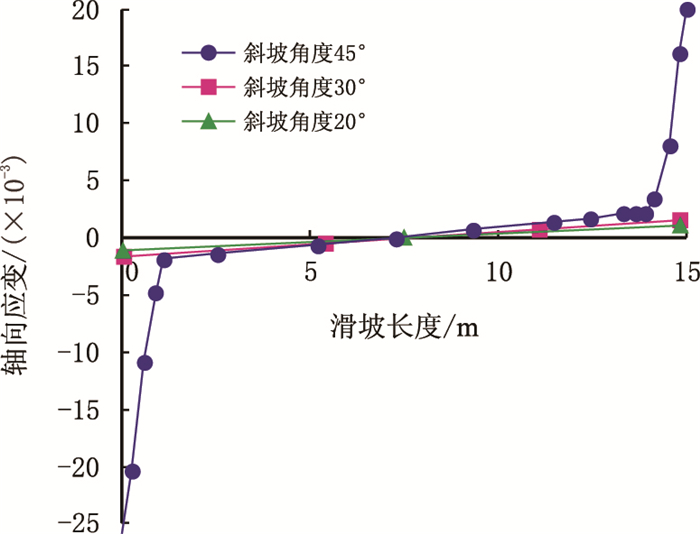 |
| 图4 管道应变随滑坡长度变化 Fig. 4 Curves of the pipeline strains varied with the length of landslips |
图 3和图 4中滑坡长度为零的坐标处是管道所处滑坡底端,滑坡长度为15.0 m是管道所处滑坡顶端,见管土有限元力学模型图 2所示。
从图 3和表 1可知,当滑坡长度为15.0 m,斜坡角度为20°,30°时,埋地管道内的最大应力分别为372 MPa和456 MPa,并没有达到其管道的屈服应力485 MPa。计算可知,管道滑坡底端的部分受到压应力,滑坡顶端的受到拉应力,与理论解释符合较好,其压应力数值稍大于拉应力的数值。由图 3可知,管道的中部Von Mises应力相对最小,所以其应变也非常的小(图 4)。管道的应变随着斜坡角度的增加、Von Mises应力的增大而相应增大,滑坡底端和顶端的应变相差不大。
当斜坡角度达到45°时,管道底端的最大Von Mises应力为530 MPa,大于屈服应力485 MPa,说明此时管道底端出现了塑性变形,由图 4中的应变曲线可知,其应变的最大值主要集中在管道的两端,特别是管道底端,出现了一定量的塑性变形区。
从表 1中可见,当滑坡长度等于30.0 m时,斜坡角度大于20°时,套管内的应力均大于管道的屈服应力,即均发生塑性变形。如果逐渐缩短滑坡长度,则套管内的应力将减小,当滑坡长度减小到20.0 m时,斜坡角度大于30°后,套管内均发生屈服应力,即进入塑性变形。因此,对于任意斜坡角度,总能计算出某一滑坡长度,满足套管不发生屈服应力。
3 应用实例根据西部某段埋地管道的土坡结构,该段斜坡角度为20°,根据本文建立的埋地管道与土壤相互作用的有限元力学模型(图 2),通过大量计算,可得管道内的最大Von Mises应力随滑坡长度的变化关系曲线如图 5所示。
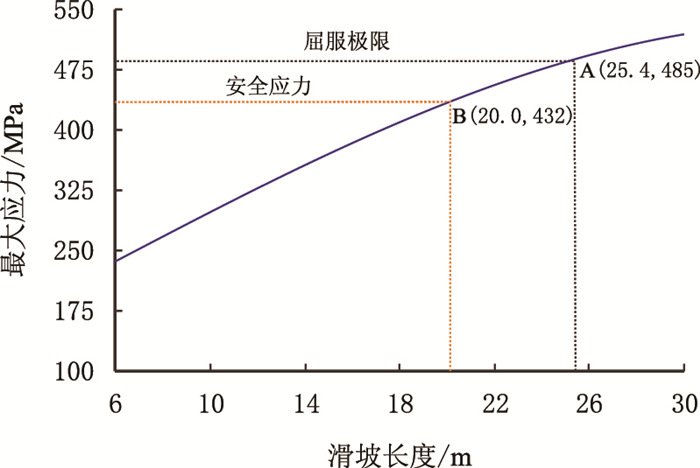 |
| 图5 管道内Von Mises应力随滑坡长度的变化关系曲线(斜坡角度为20°) Fig. 5 Curves of pipeline Von Mises stresses varied with the length of landslips (slope angle with 20 degree) |
图 5可以看出,管道内的应力与滑坡长度的增加呈非线性增加的关系,图中A点为管道的屈服应力点,也就是说滑坡长度为25.4 m时,管道内开始出现塑性变形。因此,在理论上,设计滑坡段长度必须小于25.4 m,在实际应用中,取安全系数为1.25,则设计的安全滑坡段长度为20.0 m,此时的Von Mises为432 MPa,即图 5中的B点。图 5中出现非线性关系的曲线,主要原因是埋地管道受到土壤郎肯模型的压力、土壤自重、管道自重、管道与土壤之间摩擦力以及管道的内压力等的综合作用,使得其埋地管道受力与滑坡长度呈非线性关系。
本文研究得出的安全滑坡段长度设计为西部某段埋地管道的防滑挡板或者抗滑桩提供了理论依据,并在现场得到了应用,目前该分析方法和设计结果正在南方某类似斜坡地段的埋地管道中推广应用。
4 结论与建议(1)本文建立的埋地管道与土壤相互作用的有限元力学模型,能够正确模拟计算不同斜坡角度和不同滑坡长度时,管道内的应力变化,为滑坡段长度的设计提供了简便的方法。
(2)管道内的最大Von Mises应力随滑坡长度和斜坡角度的增加而增大。
(3)埋地管道斜坡角度为20°时,其滑坡长度控制在25.4 m以内,可以保证管道内不发生塑性变形。
(4)出现塑性应变时,应力更多地集中在管道的两端,较大的应变发生在管道的上下两端。所以当出现滑坡时,管道的潜在危险区在管道的两端。
(5)当斜坡角度等于20°时,保证安全系数为1.25,则滑坡长度为20.0 m,建议每隔不到20.0 m设计防滑的挡板或者抗滑桩,斜坡角度越大,要求防护措施的间隔越密。
| [1] |
许学瑞, 帅健, 肖伟生. 滑坡多发区管道应变监测应变计安装方法[J].
油气储运, 2010, 29 (10) : 780–784.
Xu Xuerui, Shuai Jian, Xiao Weisheng. The installation method of strain gage used to monitor pipeline strain in landslide-prone areas[J]. Oil & Gas Storage and Transportation, 2010, 29 (10) : 780–784. |
| [2] |
李华, 徐震, 杨永和, 等. 滑坡作用下的埋地管道强度失效分析[J].
化工设备与管道, 2012, 49 (6) : 54–57.
Li Hua, Xu Zhen, Yang Yonghe, et al. Strength failure analysis of buried piping loaded with landslide[J]. Process Equipment & Piping, 2012, 49 (6) : 54–57. |
| [3] |
史飞. 滑坡作用对大直径埋地管道的力学性能分析[J].
山西建筑, 2012, 38 (29) : 112–114.
Shi Fei. On analysis of dynamic performance of largediameter buried pipelines under effect of landslides[J]. Shanxi Architecture, 2012, 38 (29) : 112–114. |
| [4] | (苏)勃洛达夫金.埋地管道[M].冯亮, 译.北京:石油工业出版社, 1980. |
| [5] |
杨育文, 肖建华. 土钉墙桩排组合支护基坑土压力和变形分析[J].
地下空间与工程学报, 2011, 7 (4) : 711–716.
Yang Yuwen, Xiao Jianhua. Earth pressure and displacement of combined retaining structures from piles plus soil nailing walls[J]. Chinese Journal of Underground Space and Engineering, 2011, 7 (4) : 711–716. |
| [6] |
李林, 李锁平. 圆弧形滑坡反分析技术研究[J].
地质灾害与环境保护, 2001, 12 (4) : 53–55.
Li Lin, Li Suoping. The back analysis for circular slip[J]. Journal of Geological Hazards and Environment Preservation, 2001, 12 (4) : 53–55. |
| [7] |
熊健, 邓清禄, 张宏亮, 等. 崩塌落石冲击荷载作用下埋地管道的安全评价[J].
安全与环境工程, 2013, 20 (1) : 108–114.
Xiong Jian, Deng Qinglu, Zhang Hongliang, et al. Safety assessment on the response of buried pipeline caused by rockfall impact load[J]. Safety and Environmental Engineering, 2013, 20 (1) : 108–114. |
| [8] |
付俊鹏, 马贵阳. 饱和含水冻土区埋地管道水热耦合数值模拟[J].
西安石油大学学报:自然科学版, 2011, 26 (6) : 66–69, 82.
Fu Junpeng, Ma Guiyang. Numerical simulation of waterthermal coupling of porous frozen-soil around buried pipeline in saturated water frozen-soil area[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2011, 26 (6) : 66–69, 82. |
| [9] |
李新慧. 天然气埋地管道沉降的有限元分析[J].
岩土工程学报, 2013, 35 (Supl.1) : 259–263.
Li Xinhui. Finite element analysis of settlement of buried natural gas pipelines[J]. Chinese Journal of Geotechnical Engineering, 2013, 35 (Supl.1) : 259–263. |
| [10] |
马彬, 帅健, 刘德绪, 等. 基于有限元法对爆破试验预测埋地管道极限载荷的准确性分析[J].
天然气工业, 2013, 33 (6) : 108–112.
Ma Bin, Shuai Jian, Liu Dexu, et al. A finite-elementbased analysis of the accuracy in bursting tests predicting the ultimate load of a buried pipeline[J]. Natural Gas Industry, 2013, 33 (6) : 108–112. |
| [11] |
王凯, 李清平, 宫敬, 等. 半埋热油管道传热研究[J].
西南石油大学学报:自然科学版, 2012, 34 (2) : 173–179.
Wang Kai, Li Qingping, Gong Jing, et al. Study on heat transfer of partially buried hot oil pipeline[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34 (2) : 173–179. |
| [12] |
谭东杰, 施宁, 李亮亮, 等. 洪水冲击流动管道基于DQM的临界长度研究[J].
西南石油大学学报:自然科学版, 2013, 35 (4) : 173–179.
Tan Dongjie, Shi Ning, Li Liangliang, et al. Research on critical length of flood impacting pipeline within internal flow based on differential quadrature method[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (4) : 173–179. |
| [13] |
孙宝财, 武建文, 李雷, 等. 改进GA-BP算法的油气管道腐蚀剩余强度预测[J].
西南石油大学学报:自然科学版, 2013, 35 (3) : 160–167.
Sun Baocai, Wu Jianwen, Li Lei, et al. Prediction of remaining strength of corroded and gas pipeline based on improved GA-BP algorithm[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2013, 35 (3) : 160–167. |
| [14] |
李渊博, 王建华, 张国涛, 等. 岩土崩塌冲击作用下埋地管道应力与变形分析[J].
后勤工程学院学报, 2012, 26 (6) : 31–35, 65.
Li Yuanbo, Wang Jianhua, Zhang Guotao, et al. Analysis of the buried pipeline stress and deformation due to the impact load of landslide[J]. Journal of Logistical Engineering University, 2012, 26 (6) : 31–35, 65. |
| [15] |
金浏, 李鸿晶. 逆冲断层作用下埋地管道屈曲分析[J].
工程力学, 2011, 28 (12) : 98–104.
Jin Liu, Li Hongjing. Buckling analysis of buried pipeline subject to reverse fault crossings[J]. Engineering Mechanics, 2011, 28 (12) : 98–104. |
| [16] |
尚尔京, 于永南. 地层塌陷区段埋地管道变形与应力分析[J].
西安石油大学学报:自然科学版, 2009, 24 (4) : 46–49, 57.
Shang Erjing, Yu Yongnan. Deformation and stress analysis of the buried pipeline in formation collapse region[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2009, 24 (4) : 46–49, 57. |
| [17] |
童华, 祝效华, 练章华, 等. 坍塌和冲沟作用下埋地管道大变形分析[J].
石油机械, 2007, 35 (11) : 29–32.
Tong Hua, Zhu Xiaohua, Lian Zhanghua, et al. Large deformation analysis of buried pipelines under the condition of collapse and gulch[J]. China Petroleum Machinery, 2007, 35 (11) : 29–32. |
| [18] |
王晓霖, 帅健, 张建强. 开采沉陷区埋地管道力学反应分析[J].
岩土力学, 2011, 32 (11) : 3373–3378, 3386.
Wang Xiaolin, Shuai Jian, Zhang Jianqiang. Mechanical response analysis of buried pipeline crossing mining subsidence area[J]. Rock and Soil Mechanics, 2011, 32 (11) : 3373–3378, 3386. |
| [19] |
王国丽, 张宏, 韩景宽, 等. 冻土区埋地管道基于应变设计方法研究[J].
石油规划设计, 2013, 24 (5) : 1–3, 7.
Wang Guoli, Zhang Hong, Han Jingkuan, et al. Strainbased design method for the buried pipeline in the permafrost terrain[J]. Petroleum Planning & Engineering, 2013, 24 (5) : 1–3, 7. |
 2014, Vol. 36
2014, Vol. 36

