2. 中国石油塔里木油田分公司库车勘探开发项目经理部, 新疆 库尔勒 841000;
3. 中国石油大港油田分公司石油工程研究院, 天津 大港 300280
2. The Department of Kuche Exploration and Development Project, Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China;
3. Petroleum Engineering Research Institute, Dagang Oilfield Company, PetroChina, Dagang, Tianjin 300280, China
气体钻井是以气体作循环介质携带岩屑的钻井技术,作为欠平衡钻井技术的一个分支,因其钻速快、对储层伤害小的显著特点倍受人们关注并推广应用[1]。勘探开发形势的需要推动着井型的演变与发展,这也对气体钻井技术的适应性和气体钻井过程中的机械钻速提出了更高的要求。目前对气体钻井牙轮钻头井底流场的研究很少,大部分针对井底流场的模拟都是以液体作为循环介质的钻井技术,且多以分析喷距、喷嘴组合、喷嘴形状等因素对井底流场的影响为主,气体钻井牙轮钻头在钻井过程中不涉及辅助破岩的情况,因此井底清岩能力和切削齿切削效率对机械钻速有更大影响[2-4]。鉴于此,本文基于CFD技术,对气体钻井的牙轮钻头井底流场进行了数值模拟,弄清了气体钻井牙轮钻头喷嘴侧倾角、前倾角和后倾角对井底流场特性的影响,为气体钻井系列牙轮钻头的设计、评价以及现场气体钻井的提速技术措施提供理论指导。
1 计算模型 1.1 数学模型气体钻井三牙轮钻头井底流场是一个非常复杂的三维紊流场,本文以空气作为计算介质,空气在高压下视为可压缩气体,非稳态的连续方程和N-S方程对于这种复杂紊流的瞬时运动是适用的[5-8]。控制方程由四项组成:瞬态项、对流项、扩散项和源项,其通用形式为
| $ \frac{{\partial \left( {\rho \mathit{\Phi }} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{u}}\mathit{\Phi }} \right){\rm{ = div}}\left( {\mathit{\Gamma }{\rm{grad}}(\mathit{\Phi })} \right){\rm{ + }}S $ | (1) |
式中:ρ-流体密度,kg/m3;Φ-通用变量,可代表温度、速度等求解变量;t-时间,s;u-速度矢量,m/s;Γ-广义扩散系数;S -广义源项。
气体经牙轮钻头喷射向井底再进入环空,钻头始终绕轴心线顺时针旋转,井底流场呈现显著的湍流流动并含有旋转及高曲率的情况,故采用可实现k-ε模型使控制方程封闭[5-8]。关于湍动能k和耗散率ε的运输方程为
| $ \rho \dfrac{{{\rm{d}}k}}{{{\rm{d}}t}}\! =\! \dfrac{\partial }{{\partial {x_i}}}\left[{\left( {\mu \! +\! \dfrac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}} \right)\dfrac{{\partial k}}{{\partial {x_i}}}} \right] \! +\! {G_{\rm{k}}} \! +\! {G_{\rm{b}}} \! -\! \rho \varepsilon \! -\! {Y_{\rm{M}}} $ | (2) |
| $ $\[\begin{array}{l} \rho \frac{{{\rm{d}}\varepsilon }}{{{\rm{d}}t}} = \frac{\partial }{{\partial {x_i}}}\left[{\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{ \mathsf{ ε} }}}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + \rho {{\rm{C}}_1}S\varepsilon -\\ \rho {{\rm{C}}_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {{\rm{C}}_{{\rm{1 \mathsf{ ε} }}}}\frac{\varepsilon }{k}{{\rm{C}}_{{\rm{3 \mathsf{ ε} }}}}{G_{\rm{b}}} \end{array}\]$ $ | (3) |
式中:k-单位质量湍动能,m2/s2;µ-黏度,Pa·s;µt-湍动黏度,Pa·s;σk-湍动能对应的普朗特数,无因次;Gk-平均速度梯度引起的湍动能产生项,N/(m2·s);Gb-浮力影响引起的湍动能产生项,N/(m2·s);ε-单位质量湍动能耗散率,m2/s3;YM -可压缩湍流脉动膨胀对总的耗散率的影响,kg/(m·s3);σε-湍动耗散率对应的普朗特数,无因次;ν-分子运动黏性系数,m2/s;C1,C2,C1ε,C3ε-常数,无因次;下标i=x,y,z。
对模型的求解基于有限体积法,采用二阶迎风格式将上述方程组离散,并选用PISO算法进行压力速度耦合[5-8]。
1.2 物理模型实际的牙轮钻头结构异常复杂,为了得到更加反映实际、更加可靠的气体钻井牙轮钻头的井底流场模拟结果,按实际尺寸建立牙轮钻头三维模型,钻头为三牙轮钻头,钻头直径215.9 mm,钻头有3个侧喷嘴,喷嘴形状为直圆柱型,喷嘴直径20.0 mm。建立的牙轮钻头三维模型如图 1所示。
 |
| 图1 三牙轮钻头三维实体模型图 Fig. 1 3D model of cone bit |
井底流场的物理模型为所建立牙轮钻头三维模型的反模型,为了方便计算和网格的划分,提高计算的精度和收敛性,忽略对井底流场影响较小的次要因素,做了以下假设:(1)假设井底为平面,井壁为规则圆柱面;(2)不考虑气体所受重力的影响;(3)不考虑岩屑对流场的影响,即为单向流;(4)假设流场系统为绝热系统,即与外界无热交换;(5)不考虑钻头上部接头部分的流场,只取钻头体下部的主要部分进行模拟;(6)不考虑钻头牙齿对流场的影响,模拟计算时忽略钻头牙齿。
2 定解条件的设定定解条件的设定过程为:(1)入口边界条件:截至距离喷嘴出口10 mm处为入口边界,取流量为150 m3/min(即质量流量为3.5 kg/s),设置入口湍动能k和湍动ε。(2)出口边界条件:取出口为完全出流(outflow),其值为1。(3)壁面边界条件:内壁面(牙轮表面)设置成滑移边界,外壁面(井壁)设置成固定边界,近壁面处采用壁面函数法。(4)动网格条件:激活动网格模型,给定角速度10.47 rad/s,设定3种动网格运动的方法来更新变形区域的体网格。
3 模拟结果分析 3.1 喷嘴侧倾角对井底流场的影响喷射角度定义为岩石平面垂线与喷射方向线的夹角(锐角),如图 2中的角α。喷嘴的倾斜方向与喷嘴的前进方向有几种不同搭配方式,一般分为前进、后退和侧移,以此衍生出喷嘴的前倾角、后倾角和侧倾角[9],如图 3所示。
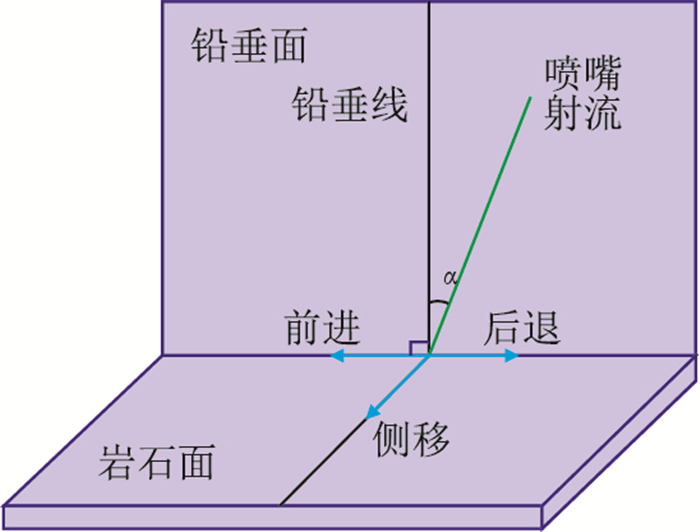 |
| 图2 喷嘴移动方向与岩石表面关系 Fig. 2 Relationship between the direction of nozzle and rock surface |
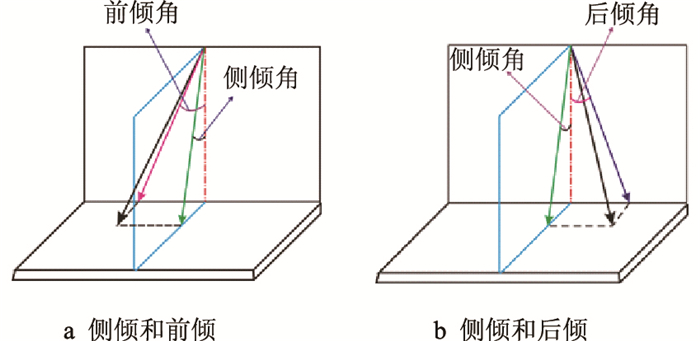 |
| 图3 喷嘴前倾角、后倾角和侧倾角示意图 Fig. 3 The front rack angle, back rack angle and the side rack angle of nozzle |
在只存在侧倾角的前提下,即前倾角和后倾角都为零,本文分别对三喷嘴具有相同侧倾角和不同侧倾角的情况进行了模拟。如图 4所示,是相同侧倾角和不同侧倾角情况下井底平面流场速度矢量图,其中相同侧倾角设置为侧倾7°,不同侧倾角设置为分别侧倾2°,7°,12°。
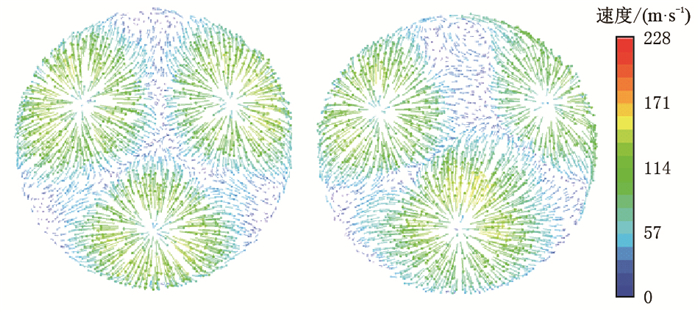 |
| 图4 三喷嘴复合侧倾角的井底平面流场速度矢量图 Fig. 4 Velocity vectors of nozzles with side rack angle in bottom hole plane |
由图 4可以看出,相同侧倾角的井底流场中心滞留区流体滞留明显,横向滞留区域较大,流体滞留时间较长,各喷嘴之间的相互干涉作用较大,射流对井底的有效冲蚀面积较小,井底岩屑容易滞留,不易及时脱离基岩进入环空,会产生重复切削;而不同侧倾角井底流场特性明显更优,中心几乎不存在流体滞留区,只有少量的横向滞留区,但流体的滞留并不明显,滞留时间较短,各喷嘴之间的相互干涉作用较小,射流对井底的有效冲蚀面积增大,井底岩屑脱离基岩速度快,不易产生重复切削,7°和12°喷嘴之间横向漫流区在接近井壁处出现了涡旋,增加了流场外扩区的紊动度,有利于岩屑的清除。
改变喷嘴的位置和侧倾角度,使3股射流轴心不在一个半径上,可大幅度增大射流对井底的有效冲蚀面积,更加有利于井底清岩。图 5为不同射流轴心圆产生的射流井底作用面积图,其中,图 5a表示3股射流轴心在同一个半径上,图 5b表示3股射流轴心在不同的半径上,图中,R为井眼半径,R1、R2、R3、R4为射流轴心圆半径,桔黄色部分为射流冲击区域。
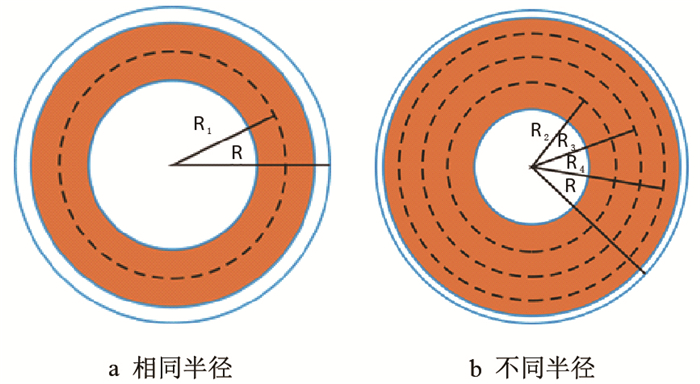 |
| 图5 不同射流轴心圆产生的射流井底作用面积图 Fig. 5 Acting surfaces of circles in different jet axis |
只存在侧倾角的射流形式,气流径直在牙轮之间流向井壁角落,不能对牙轮切削结构进行冲刷和清洗,会一定程度降低切削效率,如果地层出水,还会产生钻头泥包,影响正常钻进[10-13]。同时考虑气体钻井牙轮钻头钻进过程中的井底清岩和切削结构清洗效应,可以复合相应的前倾角和后倾角,复合前倾角和后倾角的原则是基于牙轮切屑齿的位置和形状决定的,并根据侧倾角的大小调节前倾角和后倾角的大小,使得射流轴心线与牙轮外轮廓线的切线平行,能够在起到井底清岩作用的同时也便于清洁牙轮上的切屑齿,提高切屑效率,以至通过井底流场的优化最大限度地提高机械钻速[14-16]。按照建立的实体钻头模型,根据前、后倾角的复合原则,在3个喷嘴的侧倾角分别是2°,7°,12°的基础上设定前倾角和后倾角为5°,10°,15°,大小与侧倾角成正相关,即侧倾角越大,复合的前、后倾角也就越大。
3.2.1 三喷嘴复合前倾角、后倾角复合前倾角(后倾角)的井底平面速度流场图和三维速度流场图如图 6、图 7所示。
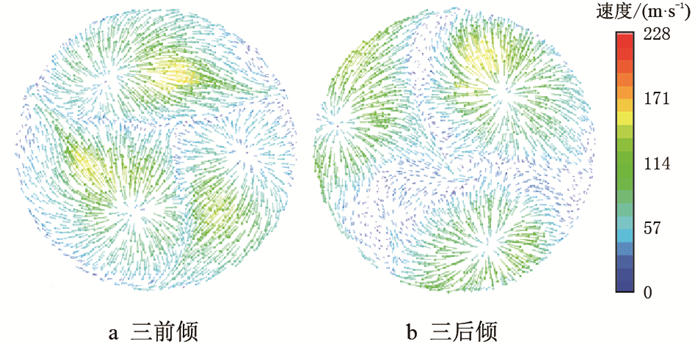 |
| 图6 三喷嘴复合前倾(后倾)角井底平面速度流场图 Fig. 6 Velocity vectors of nozzles with front rack rack or back rack angle in bottom hole plane |
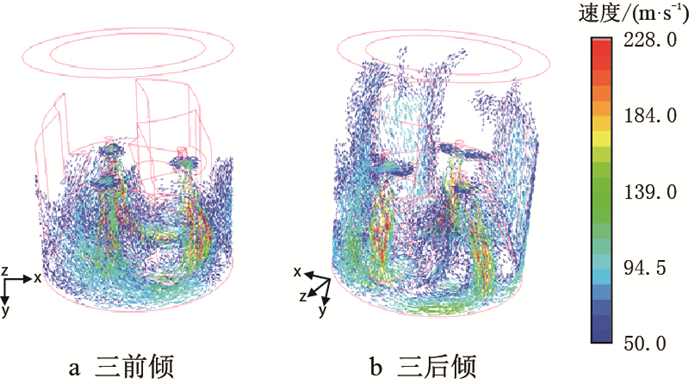 |
| 图7 三喷嘴复合前倾(后倾)角三维速度流场图 Fig. 7 3D velocity vectors of nozzles with front rack rack or back rack angle |
由图 6可知,三喷嘴复合前倾角(简称三前倾,下同)井底流场特性比三喷嘴复合后倾角(简称三后倾,下同)井底流场特性更优,前者基本无流体滞留区,各喷嘴之间的干涉作用很小,漫流场几乎覆盖了整个井底平面,漫流速度快,在钻头顺时针旋转的过程中,射流按前进方式移动,加强了气流对井底岩屑的离心作用,提高了井底的紊动度,岩屑容易被翻转带出;后者存在中心滞留区和横向滞止区,各喷嘴之间的干涉作用较大,漫流速度较慢,漫流场有效作用面积较小,射流存在前进和后退两种移动方式,对钻头旋转产生的离心作用有所削弱,不利于井底岩屑的排出。
如图 7所示,三前倾和三后倾的三维速度场对比可知,前者产生的射流主要成一股按前进方向移动,漫流层的有效高度更大,漫流以一定角度倾斜冲向井壁,然后呈现明显的上扬趋势,更利于井底岩屑脱离基岩快速运移进入环空,但气流能量消耗较大,进入环空后的速度降低,对环空岩屑的举升有影响,若要保证环空的携岩效果,需加大气体排量;后者射流呈现两股状态,前进方向的一股也具有上扬效应,并且两射流的前进方向和后退方向的两股射流在环空汇聚,产生频率叠加效应,增加了环空的紊动度,有利于环空携岩。
图 8所示是三喷嘴复合前倾角(后倾角)的三维速度流场流线图。
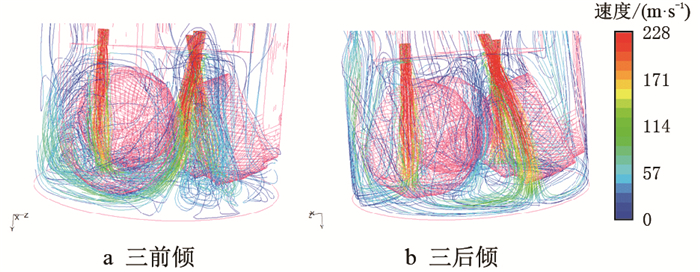 |
| 图8 三喷嘴复合前倾(后倾)角的三维速度流场流线图 Fig. 8 3D velocity streamlines of nozzles with front rack rack or back rack angle |
从图 8可以看出,三前倾射流对牙轮切削结构的清洗效果明显不如三后倾的好,前者因为复合前倾角在钻头旋转离心作用的影响下,一定程度上加快了射流按前进方式的移动速度,使得由喷嘴喷射出的气流动力部分被牙轮轮体阻挡碰撞,这部分气流能量被损失而未作用于切削结构,因此图中速度进口到井底平面间的速度流线发生了一定程度的阻挡性弯曲;而后者,并未出现这种情况,三后倾射流的能量几乎都用于清洗牙轮切屑结构和井底清岩,气流动力未被牙轮轮体阻挡而损失,速度流线也未发生阻挡性弯曲,因此对牙轮切屑结构的清洗效果更好。这也解释了图 7中三前倾三维流场速度矢量图所呈现的环空速度能量下降的问题,模拟结果显示,三前倾在井底平面直射点的最大静压力明显比三后倾在井底平面直射点的最大静压力小,再次印证了上面的分析。
3.2.2 三喷嘴混合复合前倾角和后倾角为了更加明了前倾角和后倾角对井底流场的影响,进一步对三喷嘴混合复合前倾角和后倾角的井底流场进行了模拟(图 9,图 10)。
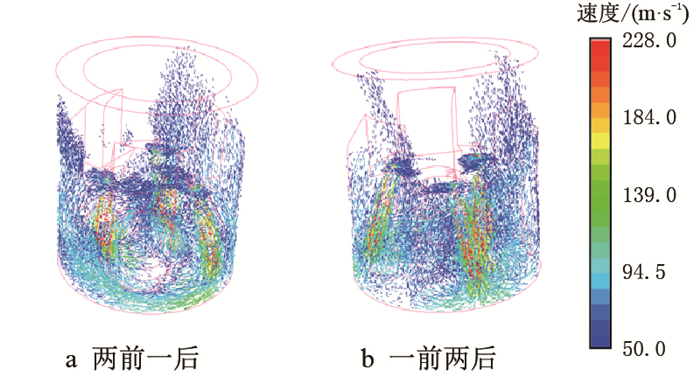 |
| 图9 三喷嘴混合复合前倾、后倾角的井底平面速度流场图 Fig. 9 Velocity vectors of nozzles with mixed composite front rake angle and back rake angle in bottom hole plane |
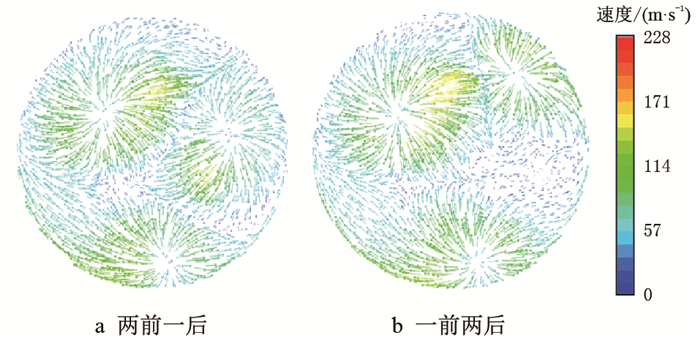 |
| 图10 三喷嘴混合复合前倾、后倾角的三维速度流场图 Fig. 10 3D velocity vectors of nozzles with mixed composite front rake angle and back rake angle |
图 9a是2°、7°侧倾角分别复合5°、10°前倾角+12°侧倾角复合15°后倾角(两前一后)的井底平面速度流场图;图 9b是2°侧倾角复合5°前倾角+7°、12°侧倾角复合10°、15°后倾角的(一前两后)井底平面速度流场图。其中,图 9a两前一后的井底平面流场特性与图 6a三前倾的井底平面流场特性差不多,同时比图 9b一前两后的井底平面流场特性好,但图 9b一前两后的井底平面流场特性又比图 6b三后倾的井底平面流场特性好。图 10a、图 10b分别对应图 9a和图 9b情况下的三维速度流场图。图 10a两前一后的三维流场速度能量明显比图 7a三前倾的三维流场速度能量强,即图 10a两前一后的三维流场环空携岩能力比图 7a三前倾的三维流场环空携岩能力强,图 10a与图 10b的三维流场速度特性差不多,但都比图 7b三后倾的三维流场环空携岩能力稍弱一些。分析表明,在气体钻井过程中,如果不改变气体排量(即保持一定的气体排量),通过三喷嘴混合复合前倾角和后倾角的方式,可以在保证一个相对较好的井底清岩能力的情况下,提高射流对牙轮切削结构的清洗能力和环空的携岩能力。
4 结论(1)三喷嘴不同侧倾角设置比相同侧倾角设置的井底流场好,更利于井底清岩;改变喷嘴的布置位置和侧倾角度,使3股射流轴心不在一个圆心上,可大幅度增大射流对井底的有效冲蚀面积,更加有利于井底清岩。
(2)三喷嘴复合前倾角比复合后倾角的井底流场特性好,井底清岩能力更强,但对牙轮切削结构的清洗效果不如后者。
(3)如果保持一定的气体排量,通过三喷嘴混合复合前倾角和后倾角方式,可以在保证一个相对较好的井底清岩能力的情况下,提高射流对牙轮切削结构的清洗能力和环空的携岩能力。
| [1] |
朱红钧, 林元华, 李强, 等. 变注入参数空气钻井流场模拟对比分析[J].
石油钻探技术, 2010, 38 (4) : 49–52.
Zhu Hongjun, Lin Yuanhua, Li Qiang, et al. Analysis of flow field in air drilling with variation of injecting parameters[J]. Petroleum Drilling Techniques, 2010, 38 (4) : 49–52. |
| [2] |
董学成, 熊继有, 黄卿卿, 等. 超高压淹没射流井底流场特性模拟分析[J].
钻采工艺, 2010, 32 (2) : 72–75.
Dong Xuecheng, Xiong Jiyou, Huang Qingqing, et al. Study of characteristic of downhole flow field under the end ironment of ultra-high pressure submerged jetting[J]. Drilling & Production Technology, 2010, 32 (2) : 72–75. |
| [3] | 赵业荣, 孟英峰, 雷桐, 等. 气体钻井理论与实践[M]. 北京: 石油工业出版社, 2007 . |
| [4] |
李玉飞, 孟英峰, 聂政远, 等. 空气钻井提高钻速机理研究[J].
石油钻探技术, 2006, 34 (4) : 9–11.
Li Yufei, Meng Yingfeng, Nie Zhengyuan, et al. The mechanisms of Increasing ROP during air drilling[J]. Petroleum Drilling Techniques, 2006, 34 (4) : 9–11. |
| [5] | 王福军. 计算流体动力学分析--CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004 . |
| [6] |
肖晓华, 朱海燕, 单世远. 气体钻井井底流场的三维数值模拟研究[J].
石油钻探技术, 2010, 38 (3) : 36–39.
Xiao Xiaohua, Zhu Haiyan, Shan Shiyuan. 3D numerical simulation of bottom hole flow field in air drilling[J]. Petroleum Drilling Techniques, 2010, 38 (3) : 36–39. |
| [7] |
熊继有, 贺培, 梁红军, 等. PDC钻头保径块结构参数流场特性模拟研究[J].
重庆科技学院学报:自然科学版, 2012, 14 (4) : 64–68.
Xiong Jiyou, He Pei, Liang Hongjun, et al. Simulation study of flow field quality on PDC bit's gauge block structure parameters[J]. Journal of Chongqing University of Science and Technology:Natural Science Edition, 2012, 14 (4) : 64–68. |
| [8] |
朱红钧, 林元华, 李强, 等. 空气钻井井眼净化与冲蚀效应模拟分析[J].
断块油气田, 2010, 17 (6) : 765–768.
Zhu Hongjun, Lin Yuanhua, Li Qiang, et al. Numerical simulation of hole cleaning and erosion effect for air drilling[J]. Fault-Block Oil & Gas Field, 2010, 17 (6) : 765–768. |
| [9] |
杨立, 杨迎新, 林敏. 横振钻井模式下PDC钻头切削齿工作角度计算[J].
天然气工业, 2008, 28 (3) : 72–74.
Yang li, Yang Yingxin, Lin Min. Calculation of PDC bit cutter working angle in transverse vibration drilling mode[J]. Natural Gas Industry, 2008, 28 (3) : 72–74. |
| [10] |
孟英峰, 练章华, 梁红, 等. 气体钻井水平井的携岩CFD数值模拟研究[J].
天然气工业, 2005, 25 (7) : 50–52.
Meng Yingfeng, Lian Zhanghua, Liang Hong, et al. CFD numerical simulation research on cuttings-carried capability in gas horizontal drilling[J]. Natural Gas Industry, 2005, 25 (7) : 50–52. |
| [11] | Zhou H, Fan H, Ji R. A comprehensive methodology of calculating hydraulic parameters in real time and the monitoring system[C]. SPE/IADC 166759, 2013. |
| [12] | Okoli U. Optimizing the technical limit value of drilling operations with proper bit selection and hydraulics[C]. SPE 167597, 2013. |
| [13] |
卓云, 胡显智, 郑霞, 等. 气体钻井遇地层出水时的充气钻井技术[J].
天然气工业, 2011, 31 (8) : 73–75.
Zhuo Yun, Hu Xianzhi, Zheng Xia, et al. Aerated drilling used during gas drilling when encountering the formation water invasion[J]. Natural Gas Industry, 2011, 31 (8) : 73–75. |
| [14] | Bu C, Qu Y, Cheng Z, et al. Numerical simulation of impact on pneumatic DTH hammer percussive drilling[J]. Journal of Earth Science, 2009, 20 (5) : 868–878. DOI:10.1007/s12583-009-0073-5 |
| [15] | El Hakam C, Felderhoff F. Cutting generation study based on cutter and design testing for improved drilling performance[C]. SPE 168737, 2013. |
| [16] |
毕雪亮, 陶丽杰, 翟洪军, 等. 空气钻井最小流量计算的修正模型[J].
断块油气田, 2008, 15 (2) : 86–87.
Bi Xueliang, Tao Lijie, Zhai Hongjun, et al. Modified model of calculating minimum flow in air drilling[J]. Fault-Block Oil & Gas Field, 2008, 15 (2) : 86–87. |
 2014, Vol. 36
2014, Vol. 36

