为了实时监测井下生产状况,越来越多的注采井都安装了长时井下压力计。通过连续测量的压力数据,工程师能够了解到井中正在发生的变化,以此进行生产调整,从而阻止意外事件发生,并优化原油开采。油田现场过去几年的经验证明,安装永久性井下压力测试设备不仅节省油井测试的成本,而且通过长时井下压力测试数据的解释还可获得额外的井筒和储层信息。目前,长时井下压力监测在提高油藏和油井管理方面正发挥着越来越重要的作用[1-4]。
在长时井下压力监测数据的解释过程中,准确确定流量变化对应的时间是获得可靠试井解释结果的关键之一。由于流量改变会引起压力的突然变化,因此通过识别压力数据的突变点可以确定出流量变化对应的时间。长时井下压力监测数据量大,采用传统的手工划分流动过程方法费时费力,自动识别流动过程正成为研究长时井下监测数据处理与解释的重要手段[5-8]。通过对比小波模极大值方法与噪声鲁棒微分算法,研究了长时井下压力监测数据流动过程的自动识别方法,取得了很好的效果。
1 小波模极值方法近年来,由于石油行业对长时井下监测技术的需求和应用越来越多,如何高效地处理和解释长时井下监测数据以获得更多的井下/油藏信息已成为目前的一个发展趋势。被广泛用于信号分析、图像处理、机械故障诊断等领域的小波变换方法,由于其具有良好的时频特性,目前正逐步被用于这类长时井下监测数据的处理过程中[9-11]。
小波变换是将母小波函数
| $ {{\psi }_{a, b}}\left( t \right)={{\left| a \right|}^{-\frac{1}{2}}}\psi \left( \frac{t-b}{a} \right) $ | (1) |
| $ \begin{align} & {{W}_{\text{f}}}\left( a, b \right)=\left\langle f\left( t \right), {{\psi }_{a, b}}\left( t \right) \right\rangle = \\ & {{\left| a \right|}^{-\frac{1}{2}}}\int{{}}_{-\infty }^{\infty }f\left( t \right)\bar{\psi }\left( \frac{t-b}{a} \right)\text{d}t \\ \end{align} $ | (2) |
式中:t-时间;a-伸缩(尺度)因子,b-平移因子;
若将小波函数看作某个平滑函数的一阶导数,则信号经过小波变换后其模的局部极值点与信号突变点对应;若将小波函数看作某个平滑函数的二阶导数,则信号经过小波变换后其模的过零点同样与信号突变点相对应。因此,根据小波变换后模的局部极值点和过零点即可确定出信号突变点位置[13-15]。一般来讲,信号奇异性可分为两种类型:第一种是信号幅值在某一时刻内发生突变,造成信号不连续,幅值突变点是第一种类型的间断点;第二种是信号中幅值无突变,但其一阶微分存在突变且一阶微分不连续。
本文研究的长时井下压力监测数据中由于流量变化引起的突变点属于第一种类型。由于长时井下监测数据中可能包含离群点、噪声信号,会影响信号突变点的确定,所以在识别突变点之前数据应进行离群点剔除和降噪处理。
目前,大多采用小波模极值来识别突变点或特征点。对于小波分解的细节信号,在尺度
在小波族中,Harr小波是所有正交小波族中紧支撑性最好的小波,并且具有不连续性,与其他紧支撑性较差的正则和正交小波相比,能更精确地定位突变点。
Harr尺度函数定义为
| $ \varphi \left( t \right)=\left\{ \begin{matrix} 1 & 0\le t < 1 \\ 0 & t<0\ \text{or}\ t\ge 1 \\ \end{matrix} \right. $ | (3) |
Harr小波函数由Harr尺度函数定义,其运算表达式为
| $ {\psi \left( t \right) = \varphi (2t)-\varphi (2t-1) = \left\{ {\begin{array}{*{20}{l}} {1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le t < 1/2}\\ {-1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1/2 \le t < 1}\\ {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t < 0\;{\rm{or}}\;t \ge 1} \end{array}} \right.} $ | (4) |
经典的离散小波变换是无冗余分解,采用下采样方法,分解后的近似系数和细节系数长度随着分解尺度的增加逐渐减半,会丢失少量信息,难以实现信号精确重构。与离散小波变换不同,静态小波变换后没有对近似系数和细节系数采取下采样,分解后的系数长度保持与原信号长度一致,所以利用近似系数和细节系数能够直接重构上一层近似信号。静态小波变换采用了一种冗余小波分解的方法,不存在信息缺失,因此能精确重构信号,在每个分解尺度上都能够准确确定出突变点位置。本文采用静态Haar小波并结合小波模极大值方法对突变点识别进行研究。
2 噪声鲁棒微分算法Pavel Holoborodko提出了一种噪声鲁棒的数据处理方法,具有多项式拟合更准确、低频信号处理更精确、高频信号光滑和抑制性能更好等特点[16]。该方法假设滤波器长度为N(奇数),滤波器系数为
| $ \begin{array}{*{20}{l}} {{f_k} = f\left( {{x_k}} \right)} \end{array} $ | (5) |
其中
| $ {x_k} = {x^*} + kh $ |
| $ k =-M, \cdots, M $ |
| $ M = \frac{{N-1}}{2} $ |
式中:
式(5)的导数通式可写为
| $ f'\left( {{x^*}} \right) = \frac{1}{h}\sum\limits_{k = 1}^M {{c_k}\left( {{f_k}-{f_{-k}}} \right)} $ | (6) |
对应的频率响应为
| $ H\left( \omega \right) = 2{\rm{i}}\sum\limits_{k = 1}^M {{c_k}\sin \left( {k\omega } \right)} $ | (7) |
式中:
通过选择系数
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{{\partial ^i}H\left( \omega \right)}}{{\partial {\omega ^i}}}} \right|}_{\omega = 0}} = {{\left. {\frac{{{\partial ^i}{H_{\rm{d}}}\left( \omega \right)}}{{\partial {\omega ^i}}}} \right|}_{\omega = 0}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 0, \cdots, n}\\ {{{\left. {\frac{{{\partial ^j}H\left( \omega \right)}}{{\partial {\omega ^j}}}} \right|}_{\omega = {\rm{ \pi }}}} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 0, \cdots, m} \end{array}} \right. $ | (8) |
式中:n-多项式次数,m-系数,m=(N -3)/2。
滤波器可以计算多项式系数、光滑含噪数据,也能进一步计算光滑数据的一阶、二阶等多阶导数。在井下生产过程中,当流量发生变化时(新的流动过程),压力响应将出现突变点,其导数将呈现一个峰值。因此可以根据一阶、二阶或者多阶导数中出现的峰值位置来确定突变点位置,即新的流动过程开始的时间。
3 数值模拟实验 3.1 小波模极值方法识别突变点以表 1中的流量数据模拟了无限大均质油藏中心一口垂直井的压力响应,共包含13个流量变化过程。图 1是不含噪声的压力模拟信号,在4.50~6.00h之间存在几个短暂的流量变化过程。
| 表1 模拟流量数据 Table 1 Simulated flow rate data |
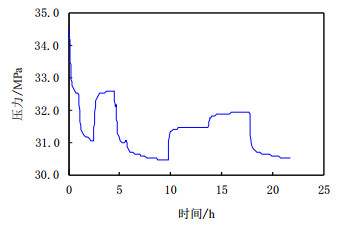 |
| 图1 模拟的压力信号 Fig. 1 Simulated pressure signal |
图 2给出了压力模拟信号经静态Harr小波进行1~6层分解后的细节系数和近似系数。流动过程突变点在小波细节系数(幅值)上体现为一个局部模极值;但随着分解尺度的增加,较小的突变点对应的模极值被“抹掉”。当分解尺度超过4层后,在采样点450~500的4个突变点以及550~600的3个突变点均萎缩成了1个突变点。因此采用高阶尺度下的模极大值来识别突变点势必会带来较大误差。
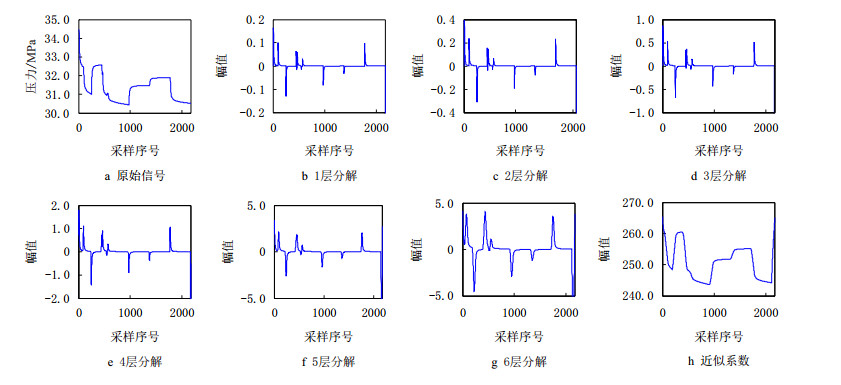 |
| 图2 静态Harr小波分解结果 Fig. 2 Decomposition by stationary harr wavelet |
分别对前3层小波分解细节系数进行搜索,找出大于预设阈值的模极大值,从而确定出突变点在各层细节系数中的位置,然后将各层细节系数的突变点位置进行匹配对比,确定最终的突变点。
表 2给出了基于模极值方法采用不同阈值对前3层小波细节系数进行识别的突变点时间(
| 表2 不同判断阈值下的突变点识别结果 Table 2 Identified break points with different threshold values |
表 3给出了在压力模拟信号中加入噪声方差为2的高斯白噪声后利用小波模极大值识别突变点的结果。
| 表3 含噪压力信号的突变点识别结果 Table 3 Identified break points from noise pressure signal |
基于Pavel Holoborodko的噪声鲁棒微分算法,采用自由度为4、长度为9的滤波器对压力模拟信号进行处理,图 3给出了一阶和二阶导数结果。从图 3可以看出,当出现一个突变点(新的流动过程)时,其一阶、二阶导数对应出现一个局部极值点。因此可以根据局部极值点确定出对应的流动过程的开始时间。从导数曲线还可以发现,局部极值的符号(正或负)可以表征流动变化:压力恢复过程对应的局部极值为正数;压力降落过程对应的局部极值为负数。因此根据局部极值还可以很容易地自动识别井下流动变化过程。
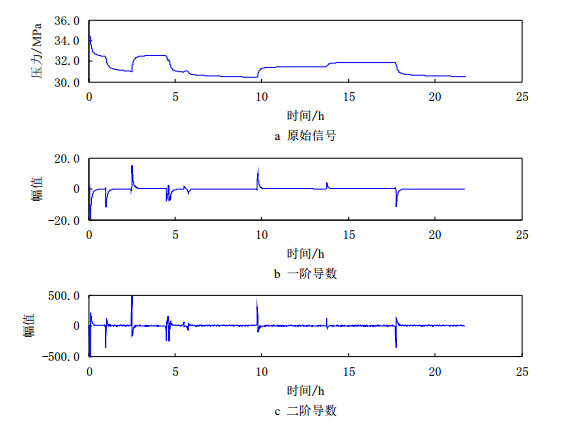 |
| 图3 模拟压力信号的导数计算结果 Fig. 3 Derivative calculation of the synthetic pressure signal |
根据上述方法,对不含噪声的压力模拟信号进行突变点识别(表 4)。从表 4可见,除了一个突变点的位置(4.73)与实际位置(4.70)存在一定误差外,采用压力数据的二阶导数可以很好地识别出突变点。采用较大的判断阈值时可能漏掉某些微小的流动过程,但主要的流动过程仍能被有效识别出来,而采用较小的阈值则可以得到较好的识别结果。在长时井下压力监测过程中,由于微小的流动过程也可能包含了更多的油藏动态信息,为了更好地捕捉这些信息,可以选择较小的阈值,但太小的阈值可能会导致误判,从而识别出多余的“假”突变点。基于数值模拟实验结果,可以选择压力信号的二阶导数、1.5倍样本标准差作为识别突变点的方法。
| 表4 含噪压力信号的突变点识别结果 Table 4 Identified break points from noise pressure signal |
为了研究噪声对突变点检测算法的影响,对原始不含噪的压力模拟信号加入噪声方差分别为1,2,5和10的白噪声。利用基于噪声鲁棒微分算法的突变点检测方法对含噪模拟数据进行识别处理(表 5),该突变点检测方法对噪声具有良好的稳健性,在信号含噪情况下能很好地识别出突变点。
| 表5 不同噪声下突变点识别结果 Table 5 Identified break points under different noise |
图 4给出了一组模拟的加噪(噪声方差为10)长时井下压力监测数据的突变点自动识别结果。从图 4中可以清楚看出,利用Pavel Holoborodko噪声鲁棒微分算法的二阶导数方法能很好地识别出所有重要的突变点。
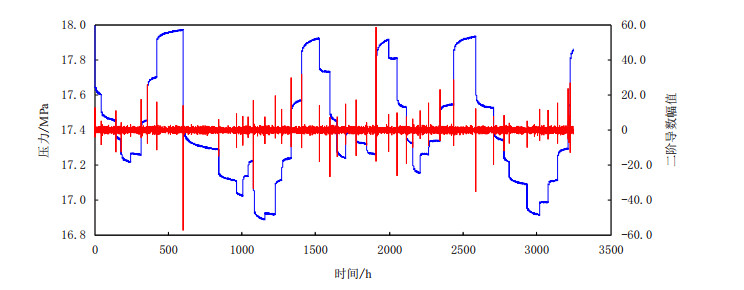 |
| 图4 模拟压力信号的导数计算结果 Fig. 4 Derivative calculation of the synthetic pressure signal |
(1) 小波模极值方法不能较好地识别出长时井下压力监测数据中的流动变化过程(突变点),存在较多的误识别和未识别点,对含噪声的信号比较敏感,在采用该方法之前必须对数据进行消噪处理。
(2) 基于噪声鲁棒微分算法的二阶导数方法可以准确、有效地识别出长时井下压力监测数据中的流动变化过程(包括较小的流动过程),并且对噪声具有稳健性,可以在不对信号进行消噪处理的情况下识别流动过程。
(3) %基于噪声鲁棒微分算法的二阶导数长时井下压力监测数据流动过程自动识别技术为长时井下监测数据的处理和解释提供了一种新的数据管理手段,具有良好的应用前景。
| [1] | Goh K F G, Gee M J, Zaini M Z, et al. Application of permanent reservoir monitoring data (DTS & PDG) in a mature offshore Malaysian oil field, for production optimisation and workover control[C]. SPE 14274, 2011. |
| [2] | Liu Yang, Horne R N. Interpreting pressure and flow rate data from permanent downhole gauges using data mining approaches[C]. SPE 147298, 2011. |
| [3] | Zheng Shiyi, Wang Fuyong. Recovering flowing history from transient pressure of permanent down-hole gauges (PDG) in oil and water two-phase flowing reservoir[C]. SPE 149100, 2011. |
| [4] |
张海燕, 熊国荣, 方伟, 等. 井下永置式测试技术在普光气田的应用[J].
天然气工业, 2011, 31 (5) : 64–66.
Zhang Haiyan, Xiong Guorong, Fang Wei, et al. Application of downhole implanted gauge testing technology in the Puguang Gas Field[J]. Natural Gas Industry, 2011, 31 (5) : 64–66. |
| [5] | Elsherif T, Balto A, Baez F, et al. The use of real-time downhole pressure and distributed temperature surveying in quantifying the skin evolution and zonal coverage in horizontal well stimulation[C]. SPE 155723, 2012. |
| [6] | Li Z, Zhu D. Predicting flow profile of horizontal well by downhole pressure and distributed-temperature data for waterdrive reservoir[J]. SPE Production & Operations, 2010, 25 (3) : 296–304. |
| [7] | Aggrey G, Davies D, Skarsholt L. A novel approach of detecting water influx time in multi-zone and multilateral completions using real-time downhole pressure data[C]. SPE 105374, 2007. |
| [8] | Suzuki S, Chorneyko D. Automatic detection of pressurebuildup intervals from permanent downhole pressure data using filter convolution[C]. SPE 125240, 2009. |
| [9] | Pico C, Aguiar R, Pires A. Wavelet filtering of permanent downhole gauge data[C]. SPE 123028, 2009. |
| [10] | Ribeiro P, Pires A, Oliveira E A P, et al. Use of wavelet transform in pressure-data treatment[J]. SPE Production & Operations, 2008, 23 (1) : 24–31. |
| [11] | Zheng Shiyi, Li Xiaogang. Analyzing transient pressure from permanent downhole gauges (PDG) using wavelet method[C]. SPE 107521, 2007. |
| [12] | 樊启斌. 小波分析[M]. 武汉: 武汉大学出版社, 2008 . |
| [13] |
刘伟, 曹思远. 基于小波变换的信号奇异性检测在层位识别中的应用[J].
石油地球物理勘探, 2010, 45 (4) : 530–533.
Liu Wei, Cao Siyuan. Application of wavelet transform based signal singularity detection in horizon identification[J]. Oil Geophysical Prospecting, 2010, 45 (4) : 530–533. |
| [14] |
吴凡, 熊高君, 叶志婵. 小波变换在信号突变点检测中的应用[J].
计算机与现代化, 2008 (8) : 133–135.
Wu Fan, Xiong Gaojun, Ye Zhichan. Applications of wavelet transform on signals catastrophe-points detection[J]. Computer and Modernization, 2008 (8) : 133–135. |
| [15] |
权建峰, 李艳, 郭东敏, 等. 小波变换模极大值方法对信号的奇异性检测[J].
探测与控制学报, 2009, 31 (2) : 46–49.
Quan Jianfeng, Li Yan, Guo Dongmin, et al. Signal singularity detection with modulus maxima method based on wavelet transform[J]. Journal of Detection & Control, 2009, 31 (2) : 46–49. |
| [16] | Pavel Holoborodko. Smooth noise-robust differentiators[EB/OL]. http://www.holoborodko.com/pavel/numerical-methods/numerical-derivative/smooth-low-noise-differentiators, 2012-12-15. |
 2014, Vol. 36
2014, Vol. 36

