2. 中海油研究总院, 北京 东城 100027;
3. 北京大学工学院, 北京 海淀 100871;
4. 中国石油大学(北京)石油工程学院, 北京 昌平 102249
2. CNOOC Research Institute, Dongcheng, Beijing 100027, China;
3. School of Engineering, Peking University, Haidian, Beijing 100871, China;
4. School of Petroleum Engineering, China University of Petroleum(Beijing), Changping, Beijing 102249, China
油气输运管线是油田开发的重要组成部分。目前主要的研究方向在管线的排布、防腐及检测方面[1-2]。事实上,管线与油田构成了一个耦合系统。因此,在油田开发过程中,需要对油气输运管线和油田采油进行统一管理。在相应的数值模拟领域,国内的研究成果还未见报道,国外也只有少数学者做了初步尝试[3-7],也没有一套成熟的算法。为此,本文给出了考虑聚合物注入过程的管线与油藏耦合数学模型,并提出了分别求解管线系统和油藏系统的解耦算法。其退化模型与商业软件的多段井(MSW)模块的对比结果说明了数学模型的正确性,与全隐式求解方法的数值对比结果则说明了解耦算法的有效性。
1 数学模型 1.1 油藏模型考虑海上油田聚合物驱油过程,数学模型满足如下假设[8-10]:(1) 油藏是等温的;(2) 岩石为微可压缩,多相渗流满足广义达西定律;(3) 流体为油水两相,共3个组分,油相中只有油组分,为黑油,水相中有水组分和聚合物组分,且各组分之间无化学反应;(4) 考虑毛管力和重力的影响。
数学模型如式(1)~式(3)所示
油组分渗流方程
| $ \nabla \cdot \left[{\dfrac{{K{K_{{\rm{ro}}}}}}{{{\mu _{\rm{o}}}{B_{\rm{o}}}}}(\nabla {p_{\rm{o}}} - {\rho _{\rm{o}}}{\rm{g}}\nabla D)} \right] + {q_{\rm{o}}} = \dfrac{\partial }{{\partial t}}\left( {\dfrac{{\phi {S_{\rm{o}}}}}{{{B_{\rm{o}}}}}} \right) $ | (1) |
水组分渗流方程
| $ \nabla \cdot \left[{\dfrac{{K{K_{{\rm{rw}}}}}}{{{\mu _{\rm{w}}}{B_{\rm{w}}}{R_{\rm{k}}}}}(\nabla {p_{\rm{w}}} - {\rho _{\rm{w}}}{\rm{g}}\nabla D)} \right] + {q_{\rm{w}}} = \dfrac{\partial }{{\partial t}}\left( {\dfrac{{\phi {S_{\rm{w}}}}}{{{B_{\rm{w}}}}}} \right) $ | (2) |
聚合物组分渗流方程
| $ \nabla \cdot \left[{\frac{{K{K_{{\rm{rw}}}}{c_{\rm{p}}}}}{{{\mu _{\rm{w}}}{B_{\rm{w}}}{R_{\rm{k}}}}}(\nabla {p_{\rm{w}}} - {\rho _{\rm{w}}}{\rm{g}}\nabla D)} \right]{\mkern 1mu} + {q_{\rm{w}}}{c_{\rm{p}}} = \frac{\partial }{{\partial t}}\left( {\frac{{\phi {F_{\rm{p}}}{S_{\rm{w}}}{c_{\rm{p}}}}}{{{B_{\rm{w}}}}}} \right) + \frac{{\partial \left[{{F_{\rm{p}}}(1 - \phi ){\rho _{\rm{r}}}{{\hat c}_{\rm{p}}}} \right]}}{{\partial t}} $ | (3) |
式中:$K$——渗透率,mD;$K_{\rm{ro}}$,$K_{\rm{rw}}$——油相和水相的相对渗透率,无因次;$p_{\rm{o}}$,$p_{\rm{w}}$——油藏油、水分压,bar(1 bar = 0.1 MPa);$q_{\rm{o}}$,$q_{\rm{w}}$——油相和水相的源汇项,m$^3$/d;${\rm{g}}$——重力加速度,g = 9.8 m/s$^{2}$;$S_{\rm{o}}$,$S_{\rm{w}}$——油、水相的饱和度,无因次;${\mu}_{\rm{o}}$,${\mu}_{\rm{w}}$——油、水相的黏度,mPa{$\cdot$}s;$B_{\rm{o}}$,$B_{\rm{w}}$——油、水相的体积系数,无因次;${\rho}_{\rm{o}}$,${\rho}_{\rm{w}}$——油、水相的密度,kg/m$^3$;$D$——高度差,m;$\phi$——岩石孔隙度,无因次;$F_{\rm{p}}$——岩石的可及体积系数,无因次;$R_{\rm{k}}$——渗透率下降系数,无因次;$c_{\rm{p}}$——油藏中聚合物的质量浓度,kg/m$^3$;${\rho}_{\rm{r}}$——岩石密度,kg/m$^3$;${\hat c}_{\rm{p}}$——单位质量的岩石上吸附的聚合物质量,kg/kg。
1.2 辅助方程考虑聚合物溶液性质对驱替过程的影响。其中,聚合溶液的黏度为聚合物浓度的多项式
| $ \mu _{\rm{p}}^0 = {\mu _{\rm{w}}}\left[{1 + ({A_1}{c_{\rm{p}}} + {A_2}c_{\rm{p}}^2 + {A_{\rm{3}}}c_{\rm{p}}^3)} \right] $ | (4) |
式中:$\mu _{\rm{p}}^0$——未经剪切情况下的聚合物溶液黏度,mPa{$\cdot$}s;${A_1}$、${A_2}$、${A_3}$——与聚合物浓度相关的黏度系数,无因次。
在聚合物溶液的流动过程中同时考虑剪切降黏和吸附滞留的影响。其中,聚合物的剪切降黏过程符合Meter和Bird方程[11];吸附滞留采用Langmuir方程;渗透率下降系数与吸附量成线性关系。
1.3 管线模型在管线模型中,整条管线可被分为若干个区段。每一个区段作为独立的控制体积,相邻区段作为该区段的边界条件。一个井段的主要控制参数包括区段长度、内径、摩擦系数以及斜度。对于每个区段都定义控制方程和相应的主变量。这样的离散型模型中,区段与区段之间的关系与油藏模型中网格之间的关系类似。 该模型中,每个区段共需要求解4个变量,分别为:压力、持液率、混合液体流速及聚合物浓度。对于每个区段共有2个持液率方程、1个浓度方程和1个压降方程。压降方程考虑了摩擦及液体加速度对流动的影响。
其中,持液率方程为
| $ \begin{array}{l} \frac{{{A_i}{L_i}}}{{\Delta t}}\left[{\left( {{\rho _l}{\alpha _l}} \right)_i^{n + 1} - \left( {{\rho _l}{\alpha _l}} \right)_i^n} \right] + {\left[{{{\left( {A{\rho _l}{v_l}} \right)}_i} - {{\left( {A{\rho _l}{v_l}} \right)}_{i + 1}}} \right]^{n + 1}} - \\ \left[{{\rho _l}{\lambda _l}{W_{\rm{I}}}\left( {{p^{{\rm{res}}}} - {p^{{\rm{seg}}}}} \right)} \right]_i^{n + 1} = 0 \end{array} $ | (5) |
假设聚合物只溶于水,浓度方程为
| $ \begin{array}{l} \frac{{{A_i}{L_i}}}{{\Delta t}}\left[ {\left( {{\rho _{\rm{w}}}{x_{{\rm{c}},{\rm{w}}}}{\alpha _{\rm{w}}}} \right)_i^{n + 1} - \left( {{\rho _{\rm{w}}}{x_{{\rm{c}},{\rm{w}}}}{\alpha _l}} \right)_i^n} \right] + \\ {\left[ {{{\left( {A{\rho _{\rm{w}}}{x_{{\rm{c}},{\rm{w}}}}{v_{\rm{w}}}} \right)}_i} - {{\left( {A{\rho _{\rm{w}}}{x_{{\rm{c}},{\rm{w}}}}{v_{\rm{w}}}} \right)}_{i + 1}}} \right]^{n + 1}} - \left[ {{\rho _{\rm{w}}}{x_{{\rm{c}},{\rm{w}}}}{\lambda _{\rm{w}}}{W_{\rm{I}}}\left( {{p^{{\rm{res}}}} - {p^{{\rm{seg}}}}} \right)} \right]_i^{n + 1} = 0 \end{array} $ | (6) |
压降方程为
| $ {\rm{R}}_{p,i}^{{\rm{seg}}} = p_i^{{\rm{seg}}} - p_{i - 1}^{{\rm{seg}}} - \left( {\Delta {p_{{\rm{h}},i}} + \Delta {p_{{\rm{f}},i}} + \Delta {p_{{\rm{a}},i}}} \right) = 0 $ | (7) |
式中:$A$——管线的截面积,m$^2$;$L$——管线的长度,m;$t$——时间,s;$\rho$——流体密度,kg/m$^3$;${\alpha}$——组分的持液率,无因次;${v}$——流体的表观速度,m/s;${\lambda}_l$——流度,mD/(mPa$\cdot$s);$W_{\rm{I}}$——井指数,mD$\cdot$m;${x}_{\rm{c,w}}$——管流水相中聚合物的质量浓度,kg/m$^3$;${p^{{\rm{res}}}}$——底部压力,bar;${p^{{\rm{seg}}}}$——井段压力,bar;$\Delta {p_{\rm{h}}}$——液柱高度导致的压差,bar;$\Delta {p_{\rm{f}}}$——摩擦力导致的压力损失,bar;$\Delta {p_{\rm{a}}}$——流体加速度导致的压差,bar;上标$n$——迭代的时间步;下标$i$——离散区段的编号;下标$l$——液相,$l$ =o油相,$l$ =w水相。
| $ {v_{\rm{o}}} = {C_{\rm{o}}}{v_{\rm{m}}} + {v_{\rm{d}}} $ | (8) |
式中:${v_{\rm{o}}}$——油相流速,m/s;${v_{\rm{m}}}$——混合流速,m/s;${C_{\rm{o}}}$——速度分布参数,无因次;${v_{\rm{d}}}$——滑脱速度,m/s。
流体在管道中流动的表观速度可表示为
| $ {v_{{\rm{so}}}} = {\alpha _{\rm{o}}}\left( {{C_{\rm{o}}}{v_m} + {v_{\rm{d}}}} \right) $ | (9) |
式中:${v_{\rm{so}}}$——油相流动的表观速度,m/s;${\alpha _{\rm{o}}}$——持油率,无因次。
由此得到考虑管线—油藏交互流动状态下的数学模型。
2 求解方法数学模型中,管线流动通过井筒炮眼与油藏流动连接在一起,构成了管线—油藏耦合流动系统。全隐式方法耦合求解算法很难求解该数学模型。原因为管线流动系统与油藏流动系统的求解方程形式存在很大差异;同时,管线区段的体积与油藏网格的体积相差3~4个数量级,使得雅可比矩阵的求解很难收敛,从而导致效率较低。因此,本文采用了单独求解管线系统和油藏系统的方法。在迭代过程中通过交换边界条件(井筒压力、射孔段流量及聚合物浓度)来完成该耦合系统的求解过程(图 1)。
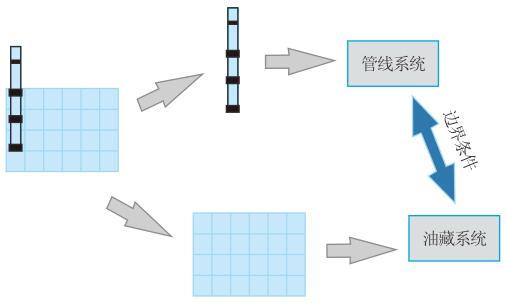 |
| 图1 耦合系统求解过程示意图 Fig. 1 Solution of coupled syste |
迭代过程中,在当前井底压力条件下,首先计算油藏压力;此后,将油藏压力带入井筒系统中,根据当前的压力或流量限制计算井筒内部各区段的压力;最后,将井筒压力带入油藏系统再次计算油藏压力;如此反复,直到方程收敛。
流量边界条件交换过程与压力过程类似。%处理时,式(1)、式(2)中源汇项等于式(5)中的井处理项,有
| $ {q_l} = {\rho _l}{\lambda _l}{W_{\rm{I}}}\left( {{p^{\rm{res}}} - {p^{\rm{seg}}}} \right) $ | (10) |
由此,实现油藏流动和管线流动的流量边界条件交换。 由于在水相中存在聚合物溶液,根据质量守恒实现聚合物溶液的浓度边界条件交换
| $ {q_{\rm{w}}}{c_{\rm{p}}} = {\rho _{\rm{w}}}{x_{\rm{c,w}}}{\lambda _{\rm{w}}}{W_{\rm{I}}}\left( {{p^{\rm{res}}} - {p^{\rm{seg}}}} \right) $ | (11) |
采用Peaceman井处理模型,表征井筒内射孔情况,其井指数 如下式所示
| $ {W_{\rm{I}}} = \frac{{2\pi Kh}}{{\mu B\left[{\ln ({r_{\rm{e}}}/{r_{\rm{w}}}) + S - 1/2} \right]}} $ | (12) |
式中:$r_{\rm{w}}$——井筒半径,m;$r_{\rm{e}}$——泄油半径,m;$S$——井筒表皮系数,无因次。
与耦合求解方法相比,解耦方法在降低雅可比矩阵规模的同时,也降低了求解的难度。一般而言,其求解速度比耦合求解方法高1~2个数量级。
3 测试算例将解耦模型与某商业软件进行对比,以验证该数学模型的正确性;通过与全隐式耦合求解算法对比,来验证解耦算法的准确性。
3.1 油田基本数据油藏区块面积为1 km$^2$,孔隙度为0.35,渗透率为100 mD。油藏被划分为11 $\times$ 11 = 121个网格。油藏初始压力为34.48 MPa,初始含水饱和度为0.25。注入井定注入量为1 590 m$^3$/d,定聚合物质量浓度为1.75 kg/m$^3$。生产井最大产量为1 590 m$^3$/d,最小井底流压为1.38 MPa。岩石的最大吸附因子为0.05,残余阻力系数为3。油密度和水密度分别为 740 kg/m$^3$和1 037 kg/m$^3$。油黏度为5 mPa$\cdot$s,水的黏度随聚合物浓度的变化而变化。
3.2 算例1油藏左侧正中网格处设置了一口直井注水井,油藏中间设置了一口两分支水平生产井(图 2),其完井水平段分别位于两个不同的油层,该井被离散为11个区段(其中两个分支的5个井段为射孔段)。
随着网格深度的增加,压力也随之增加(图 2)。越接近注入井,其压力越高。其计算结果与某商业软件非常接近。图 3显示了油藏的含油饱和度分布。由于水相密度比油相密度大,在重力作用下,油藏上部的含油饱和度比较大。从图中可见,某商业软件结果与本文提出的耦合模型的结果非常吻合。
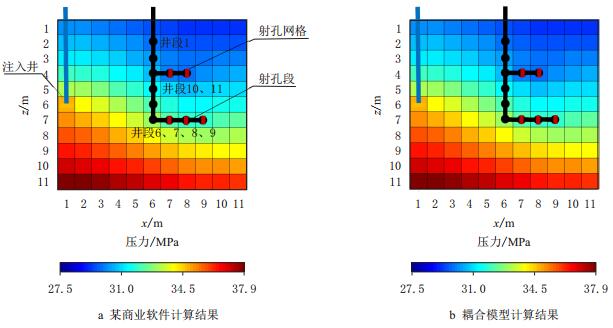 |
| 图2 某商业软件与耦合模型的压力分布对比 Fig. 2 Comparison of pressure between business software and coupled model |
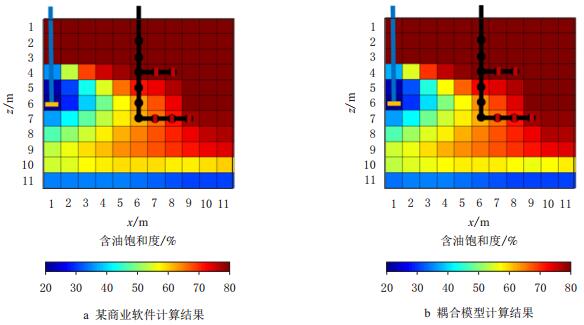 |
| 图3 某商业软件与耦合模型的含油饱和度分布对比 Fig. 3 Comparison of oil saturation between business software and coupled model |
计算对比5个射孔段(井段7,8,9,10,11)和井口处(井段1)的持油率(图 4)。 由于重力的作用,上游分支(射孔段10和11)的持油率要比下游(射孔段7,8和9)的大。井口位置的持油率是两个分支集中并混合平均的结果,其大小介于上述二者之间。对于每个射孔段,可以看出耦合模型的计算结果与某商业软件的计算结果相近。
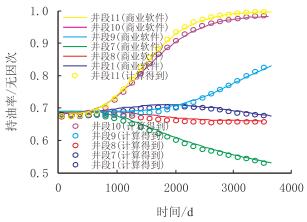 |
| 图4 某商业软件与耦合模型的井段持油率分布对比 Fig. 4 Comparison of SOHF between business software and coupled model |
通过算例1的计算结果与某商业软件的计算结果进行对比分析可以看出,利用耦合模型在计算多段井问题上与该商业软件的计算结果相近,验证了模型的正确性。
3.3 算例2在算例1的基础上,对比了耦合求解和解耦结果中的井段压力(图 5)和井段持油率(井段6)(图 6),以及油的产量(图 7)和水的产量(图 8)。从图可见,上述四项的耦合和解耦结果均重合,这证明了解耦模型具有足够的精确度。就求解的计算速度来而言,解耦方法比全耦合解法快1~2个数量级。
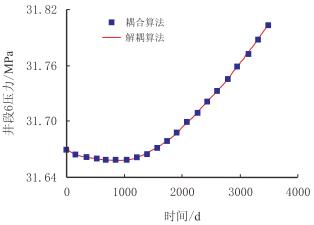 |
| 图5 耦合与解耦方法的压力变化对比 Fig. 5 Comparison of pressure between coupled and decoupled method |
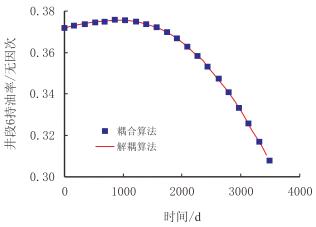 |
| 图6 耦合与解耦方法的持油率变化对比 Fig. 6 Comparison of oil hold-up between coupled and decoupled method |
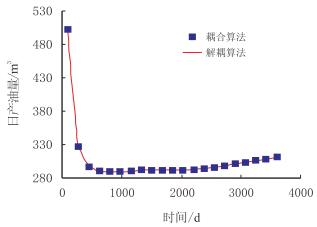 |
| 图7 耦合与解耦方法的油产量变化对比 Fig. 7 Comparison of oil production between coupled and decoupled method |
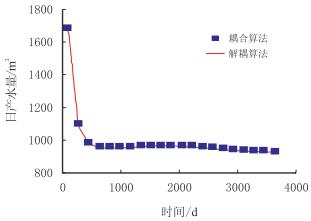 |
| 图8 耦合与解耦方法的水产量变化对比 Fig. 8 Comparison of water production between coupled and decoupled method |
(1) Drift-flux 模型可有效求解聚驱条件下管线内各项流体的流动过程,通过与某商业软件的多段井模型进行对比,计算误差小于5%,验证了数学模型的正确性。
(2) 与全隐式耦合求解算法结果对比说明,文中的解耦算法可以有效地求解管线—油藏耦合系统的流动问题,计算误差小于5%,计算速度提高1~2个数量级,有效改善了原耦合求解算法的收敛性,证明了算法的有效性。
| [1] |
杨卫明, 吴金柱, 赵峰. 埕岛油田油藏调整检测与评估[J].
中国造船, 2008, 49 (2) : 668–671.
Yang Weiming, Wu Jinzhu, Zhao Feng. Oil reservoir adjustment inspection and assessment in Chengdao Oilfield[J]. Shipbuilding of China, 2008, 49 (2) : 668–671. |
| [2] | 孙志宇, 蒲春生, 谢丽华, 等. 强磁防垢技术研究及其在油田的现场应用[J]. 石油工业技术监督, 2005, 21 (12) : 12–14. |
| [3] | Gregory G A,Aziz K. Calculation of pressure and temperature profiles in multiphase pipelines and simpne pipeline networks[C]. SPE 78-01-04, 1978. |
| [4] | Peaceman D W. Interpretation of well-block pressures in numerical reservoir simulation(includes associated paper 6988)[J]. Old SPE Journal, 1978, 18 (3) : 183–194. |
| [5] | Schlumberger GeoQuest. Eclipse technical description, multi-segment wells[R]. Schlumberger Eclipse Technical Description, 2005. |
| [6] | Schiozer D J. Simultaneous simulation of reservoir and surface facilities[D]. Stanford:Stanford University,1994. |
| [7] | Schiozer D J, Aziz K. Use of domain decomposition for simultaneous simulation of reservoir and surface facilities[C]. SPE 27876, 1994. |
| [8] | 刘玉章. 聚合物驱提高采收率技术. 北京:石油工业出版社[M]. 2006 . |
| [9] | 王健. 化学驱物理化学渗流理论与应用. 北京:石油工业出版社[M]. 2008 . |
| [10] |
曾凡辉, 郭建春, 尹建. 井筒与油藏耦合的压裂水平井非稳态产能计算模型[J].
现代地质, 2011, 25 (6) : 1159–1166.
Zeng Fanhui, Guo Jianchun, Yin Jian. An unsteady state computation model of fractured horizontal well coupling with reservoir[J]. Geoscience, 2011, 25 (6) : 1159–1166. |
| [11] |
姚军, 吴明录, 胡航. 碱-聚合物复合驱油藏流线数值试井解释模型及其应用[J].
石油学报, 2008, 29 (6) : 894–898.
Yao Jun, Wu Minglu, Hu Hang. Streamline numerical well-testing interpretation model for alkaline-polymer combination flooding reservoirs and its application[J]. Acta Petrolei Sinica, 2008, 29 (6) : 894–898. |
| [12] | Shi H, Holmes J, Durlofsky L, et al. Drift-flux modeling of two-phase flow in wellbores[J]. SPE Journal, 2005, 10 (1) : 24–33. DOI:10.2118/84228-PA |
| [13] | Shi H, Holmes J, Diaz L, et al. Drift-flux parameters for three-phase steady-state flow in wellbores[J]. SPE Journal, 2005, 10 (2) : 130–137. DOI:10.2118/89836-PA |
| [14] | Kokal S L, Stanislav J F. An experimental study of two-phase flow in slightly inclined pipes-Ⅱ. Liquid holdup and pressure drop[J]. Chemical Engineering Science, 1989, 44 (3) : 681–693. DOI:10.1016/0009-2509(89)85043-2 |
 2014, Vol. 36
2014, Vol. 36

