2. 中国石油青海油田分公司天然气处, 甘肃 敦煌 736202;
3. 中国石油西南油气田勘探开发研究院分析实验中心, 四川 成都 610000;
4. 中国石油川庆钻探工程有限公司, 重庆 江北 400020
2. Natural Gas Bureau, Qinghai Oilfield Company Petrochina, Dunhuang, Gansu 736202, China;
3. Research Institute of Exploration and Development, Petrochina Southwest Oil & Gas Field Company, Chengdu, Sichuan 610000, China;
4. Chuanqing Drilling Engineering Co. Ltd., CNPC, Jiangbei, Chongqing 400020, China
注水是最常见的提高油藏采收率的方式,许多油田都采用注水方式开发[1-2]。注水配注的研究[3-6]是指导高效注水开发的基础。一直以来,对注水量和注采比的计算方法研究是一个热门的话题。注水量与注采比的计算是相互关联,目前注水量和注采比的计算方法主要有:logistic模型法[7-9],主要适合于累积产量达到可采储量的50%时出现产量递减的油藏[7-10];水驱曲线法[11],主要用于油田生产规律出现符合水驱曲线的情况;阶段存水率图版法[12],适合于存水率变化规律显著的生产情况。上述计算方法[13]只考虑了地层压力或含水率等单个因素的影响[13],而实际开发过程中,注水量和注采比的大小将受累积水油比、地层压力和含水率等多因素的影响,针对这一问题,本文研究了两种阶段注采比的计算新方法,可综合考虑累积水油比、地层压力和含水率的影响,能够用于预测不同含水阶段在某地层压力和含水上升速度下的注采比。
1 注采比模型建立 1.1 阶段注采比关系式推导根据文献[14],注水开发油田的累积注水量与累积产油量的关系式为
| $ lg ({W_{\rm{i}}} - F) = \alpha + \beta {N_{\rm{p}}} $ |
累积注水量$W_{\rm{i}}$对时间的导数为注水量$Q_{\rm{wi}}$,累积产油量$N_{\rm{p}}$对时间的导数为产油量$Q_{\rm{o}}$,因此对式(1)两边求导,可得
| $ \dfrac{{{Q_{{\rm{wi}}}}}}{{2.303\zeta({W_{\rm{i}}} - F)}} = \beta {Q_{\rm{o}}} $ | (2) |
由式(2)变形,得
| $ {Q_{\rm{w}}}_{\rm{i}} = 2.303\zeta\beta {Q_{\rm{o}}}\left( {{W_{\rm{i}}} - F} \right) $ | (3) |
封闭未饱和油藏的物质平衡方程为
| $ {N_{\rm{p}}}{B_{\rm{o}}} = {N_{{\rm{bi}}}}{{\rm{C}}_{{\rm{eff}}}}\Delta p + {W_{\rm{i}}}{B_{\rm{w}}} - {W_{\rm{p}}}{B_{\rm{w}}} $ | (4) |
式中:
由式(4)得
| $ {W_{\rm{i}}} = \dfrac{{{N_{\rm{p}}}{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + {W_{\rm{p}}} - \dfrac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}} $ | (5) |
根据累积水油比的定义有
| $ R_{\rm{wo}}= \dfrac{{{W_{\rm{p}}}}}{{{N_{\rm{p}}}}} $ | (6) |
将式(6)代入式(5),得
| $ {W_{\rm{i}}} = {N_{\rm{p}}}\left( {\dfrac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + R_{\rm{wo}}} \right) - \dfrac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}} $ | (7) |
将式(7)代入式(3),得
| $ {Q_{\rm{w}}}_{\rm{i}}\!=\!2.303\zeta\beta{Q_{\rm{o}}}\left[{{N_{\rm{p}}}\left({\dfrac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}}\!+\!R_{\rm{wo}}} \right)\!-\!\dfrac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}}\!-\!F}\right] $ | (8) |
根据阶段注采比的定义
| $ {Q_{{\rm{wi}}}} = R_{\rm{IP}} \cdot {Q_{\rm{L}}} $ | (9) |
根据含水率的定义,有
| $ {Q_{\rm{o}}} = {Q_{\rm{L}}}(1 - {f_{\rm{w}}}) $ | (10) |
将式(9)和式(10)代入式(8),得
| $ {R_{{\rm{IP}}}} = 2.303\zeta \beta \left( {1 - {f_{\rm{w}}}} \right)\left[{{N_{\rm{p}}}\left( {\frac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + {R_{{\rm{wo}}}}} \right) - \frac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}} - F} \right] $ | (11) |
式(11)表明阶段注采比是累积产油量函数。累积产油量是油藏特征参数($A$、$h$、$\phi$ )、含水饱和度等的函数,可由采出程度与饱和度的关系式计算[10]
| $ {N_{\rm{p}}} = R \cdot {N_{{\rm{bi}}}} = \frac{{100Ah\phi }}{{{B_{{\rm{oi}}}}}}\left[{\frac{2}{3}{S_{\rm{w}}} + \frac{1}{3}\left( {1 - {S_{{\rm{or}}}}} \right) - {S_{{\rm{wi}}}}} \right] $ | (12) |
水驱油分流方程
| $ {f_{\rm{w}}} = \dfrac{{{Q_{\rm{w}}}}}{{{Q_{\rm{w}}} + {Q_{\rm{o}}}}} = \dfrac{1}{{1 + \dfrac{{{\mu _{\rm{w}}}{K_{{\rm{ro}}}}}}{{{\mu _{\rm{o}}}{K_{{\rm{rw}}}}}}}} $ | (13) |
油水相对渗透率的比值与含水饱和度通常满足指数关系
| $ \dfrac{{{K_{{\rm{ro}}}}}}{{{K_{{\rm{rw}}}}}} = {C_1}{{\rm{e}}^{ - D{S_{\rm{w}}}}} $ | (14) |
式(14)中$C_1$、$D$为待定系数,不同油藏具有不同的$C_1$、$D$值,对式(14)两边同时取对数得
| $ \ln \dfrac{{{K_{{\rm{ro}}}}}}{{{K_{{\rm{rw}}}}}} = \ln {C_1} - D{S_{\rm{w}}} $ | (15) |
利用实际油藏的相对渗透率数据,做${\rm{ln}}\left( {{K_{{\rm{ro}}}}/{K_{{\rm{rw}}}}} \right)$与$S_{\rm{w}}$的关系曲线,线性回归可求取$C_1$和$D$值。将式(14)代入式(13),得
| $ {f_{\rm{w}}} = \dfrac{{{Q_{\rm{w}}}}}{{{Q_{\rm{w}}} + {Q_{\rm{o}}}}} = \dfrac{1}{{1 + {C_1}\dfrac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{o}}}}}{{\rm{e}}^{ - D{S_{\rm{w}}}}}}} $ | (16) |
由式(16)得
| $ {S_{\rm{w}}} = - \dfrac{1}{D}\left[{\ln \left( {\dfrac{{{\mu _{\rm{o}}}}}{{C{}_1{\mu _{\mathop{\rm w}\nolimits} }}}} \right) + \ln \dfrac{{1 - {f_{\rm{w}}}}}{{{f_{\rm{w}}}}}} \right] $ | (17) |
将式(17)代入式(12),整理后可得
| $ {N_{\rm{p}}}\!=\!\dfrac{{100Ah\phi}}{{{B_{{\rm{oi}}}}}}\!\left[\!{\dfrac{1}{3}\!\left(\!{1\!-\!{S_{{\rm{or}}}}}\!\right)\!-\!{S_{{\rm{wi}}}}\!-\! \dfrac{2}{{3D}}\ln\left(\!{\dfrac{{{\mu_{\rm{o}}}}}{{{C_1}{\mu _{\rm{w}}}}}\dfrac{{1\!-\!{f_{\rm{w}}}}}{{{f_{\rm{w}}}}}}\!\right)}\!\right] $ | (18) |
将式(18)代入式(11),可得封闭油藏阶段注采比计算式
| $ \begin{array}{l} {R_{{\rm{IP}}}} = 2.303\zeta \beta \left( {1 - {f_{\rm{w}}}} \right)\left\{ {\frac{{100Ah\phi }}{{{B_{{\rm{oi}}}}}}\left( {\frac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + {R_{{\rm{wo}}}}} \right)} \right.\\ \left. {\left[{\frac{1}{3}\left( {1 - {S_{{\rm{or}}}}} \right) - {S_{{\rm{wi}}}} - \frac{2}{{3D}}\ln \left( {\frac{{{\mu _{\rm{o}}}}}{{{C_1}{\mu _{\rm{w}}}}}\frac{{1 - {f_{\rm{w}}}}}{{{f_{\rm{w}}}}}} \right)} \right] - \frac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}} - F} \right\} \end{array} $ | (19) |
油水相对渗透率比值随含水饱和度的变化除了可以用指数式描述外,还可以用其他关系式来描述,如俞启泰在统计国内外十多个水驱油藏油水相渗曲线后,认为油水相对渗透率比值与含水饱和度的关系可以用幂律关系式来描述[14]
| $ \dfrac{{{K_{{\rm{ro}}}}}}{{{K_{{\rm{rw}}}}}} = {C_2}{\left( {\dfrac{{{S_{\rm{w}}} - {S_{{\rm{wi}}}}}}{{1 - {S_{{\rm{or}}}} - {S_{\rm{w}}}}}} \right)^{ - n}} $ | (20) |
式(20)中$C_2$、$n$为待定系数,不同油藏具有不同的$C_2$、$n$值,先对式(20)两边同时取对数,再利用实际油藏的相对渗透率数据进行线性回归可求取$C_2$和$n$值。
将式(20)代入式(13),整理后得
| $ {S_{\rm{w}}} = \dfrac{{{S_{{\rm{wi}}}} + \left( {1 - {S_{{\rm{or}}}}} \right){{\left[{\dfrac{{{C_2}{\mu _{\rm{w}}}{f_{\rm{w}}}}}{{{\mu _{\rm{o}}}\left( {1 - {f_{\rm{w}}}} \right)}}} \right]}^{\frac{1}{n}}}}}{{1 + {{\left[{\dfrac{{{C_2}{\mu _{\rm{w}}}{f_{\rm{w}}}}}{{{\mu _{\rm{o}}}\left( {1 - {f_{\rm{w}}}} \right)}}} \right]}^{\frac{1}{n}}}}} $ | (21) |
将式(21)代入式(12),得
| $ {N_{\rm{p}}} = \dfrac{{100Ah\phi }}{{{B_{{\rm{oi}}}}}}\left\{ {\dfrac{2}{3}\dfrac{{{S_{{\rm{wi}}}} + \left( {1 - {S_{{\rm{or}}}}} \right){{\left[{\dfrac{{{C_2}{\mu _{\rm{w}}}{f_{\rm{w}}}}}{{{\mu _{\rm{o}}}\left( {1 - {f_{\rm{w}}}} \right)}}} \right]}^{\frac{1}{n}}}}}{{1 + {{\left[{\dfrac{{{C_2}{\mu _{\rm{w}}}{f_{\rm{w}}}}}{{{\mu _{\rm{o}}}\left( {1 - {f_{\rm{w}}}} \right)}}} \right]}^{\frac{1}{n}}}}} + \dfrac{1}{3}\left( {1 - {S_{{\rm{or}}}}} \right) - {S_{{\rm{wi}}}}} \right\} $ | (22) |
将式(22)代入式(11),可得封闭油藏阶段注采比计算式
| $ \begin{array}{l} {R_{{\rm{IP}}}} = 2.303\zeta \beta \left( {1 - {f_{\rm{w}}}} \right)\left\{ {\frac{{100Ah\phi }}{{{B_{{\rm{oi}}}}}}\left( {\frac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + {R_{{\rm{wo}}}}} \right)} \right.\\ \left. {\left[ {\frac{2}{3}\frac{{{S_{{\rm{wi}}}} + \left( {1 - {S_{{\rm{or}}}}} \right){{\left( {\frac{{{C_2}{\mu _{\rm{w}}}{f_{\rm{w}}}}}{{{\mu _{\rm{o}}}\left( {1 - {f_{\rm{w}}}} \right)}}} \right)}^{\frac{1}{n}}}}}{{1 + {{\left( {\frac{{{C_2}{\mu _{\rm{w}}}{f_{\rm{w}}}}}{{{\mu _{\rm{o}}}\left( {1 - {f_{\rm{w}}}} \right)}}} \right)}^{\frac{1}{n}}}}} + \frac{1}{3}\left( {1 - {S_{{\rm{or}}}}} \right) - {S_{{\rm{wi}}}}} \right] - \frac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}} - F} \right\} \end{array} $ | (23) |
某区块某层属于断裂遮挡单斜油藏封闭油藏,无边底水,油藏不发育裂缝,区块含油面积15.24 km$^2$,有效厚度16.71 m,有效孔隙度11.94%,原始含油饱和度为60%,原始地层压力24.9 MPa,饱和压力为12.2 MPa,地面原油密度为0.838 g/cm$^3$,地层油密度0.767 6 g/cm$^3$,地层油黏度2.5 mPa$\cdot$s,饱和压力下原油体积系数为1.180,原始压力下原油体积系数为1.160,原油压缩系数为12.3$\times$10$^{-5}$ MPa$^{-1}$,综合压缩系数为24.6$\times$10$^{-5}$ MPa$^{-1}$。地层油水相对渗透率数据见表 1,2000年至2011年生产动态数据见表 2。
| 表1 实例层油水相对渗透率数据 Table 1 Relative permeability data of the example formation |
| 表2 实例层生产动态数据 Table 2 Production dynamic data of the example formation |
利用表 1中的相渗数据,可做出油水相对渗透率比值与含水饱和度半对数曲线,分别如图 1和图 2所示,用式(14)和式(20)进行线性回归,求出系数$C_1$=252 058 1,$D$=23.46,$C_2$=1.85,$n$=1.996。因此,油水相对渗透率比值与含水饱和度的半对数与双对数关系式分别为
| $ \ln \dfrac{{{K_{{\rm{ro}}}}}}{{{K_{{\rm{rw}}}}}} = 14.74 - 23.46{S_{\rm{w}}} $ | (24) |
| $ \ln \dfrac{{{K_{{\rm{ro}}}}}}{{{K_{{\rm{rw}}}}}} = - 1.996\ln \left( {\dfrac{{{S_{\rm{w}}} - {S_{{\rm{wi}}}}}}{{1 - {S_{{\rm{or}}}} - {S_{\rm{w}}}}}} \right) + 0.615 $ | (25) |
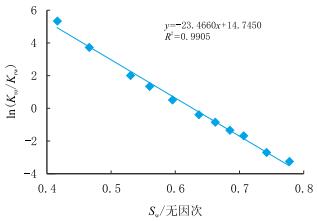 |
| 图1 油水相对渗透率比值与含水饱和度半对数曲线 Fig. 1 Semi-logarithmical curve of the relative permeability ratio of oil to water with water saturation |
 |
| 图2 油水相对渗透率比值与含水饱和度双对数曲线 Fig. 2 Bi-logarithmical curve of the relative permeability ratio of oil to water with water saturation |
根据式(1),对表 2中的累积注水量和累积产油量进行线性试差计算,拟合结果如图 3所示,求出系数$F$=0,$\alpha$=2.310 6,$\beta$=0.001 4。
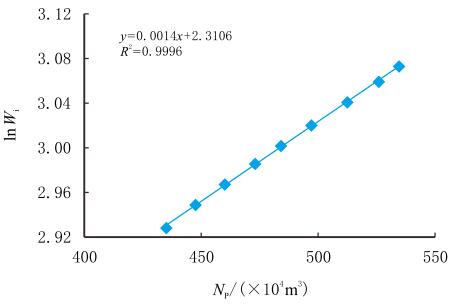 |
| 图3 累积注水量与累积产油量半对数曲线 Fig. 3 Semi-logarithmical curve of cumulative water injection with cumulative oil production |
将油藏静态参数及$C_1$、$D$、$C_2$、$n$、$\beta$等参数值代入式(19)和式(23),可得该例子油藏注采比计算的两种不同表达式
方法一
| $ \begin{array}{l} {R_{{\rm{IP}}}} = 0.0035\left( {1 - {f_{\rm{w}}}} \right)\left\{ {2621.2458\left( {\frac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + {R_{{\rm{wo}}}}} \right)} \right.\\ \left. {\left[ { - 0.1273 - \frac{2}{{70.38}}\ln \left( {\frac{3}{{2520581.029}}\frac{{1 - {f_{\rm{w}}}}}{{{f_{\rm{w}}}}}} \right)} \right] - \frac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}}} \right\} \end{array} $ | (26) |
方法二
| $ \begin{array}{l} {R_{{\rm{IP}}}} = 0.0035\left( {1 - {f_{\rm{w}}}} \right)\left\{ {2621.2458\left( {\frac{{{B_{\rm{o}}}}}{{{B_{\rm{w}}}}} + {R_{{\rm{wo}}}}} \right){\rm{ }}} \right.\\ \left. {\left[ {\frac{2}{3}\frac{{0.4 + 0.8181{{\left( {0.2449\frac{{{f_{\rm{w}}}}}{{\left( {1 - {f_{\rm{w}}}} \right)}}} \right)}^{\frac{1}{{1.996}}}}}}{{1 + {{\left( {0.2449\frac{{{f_{\rm{w}}}}}{{\left( {1 - {f_{\rm{w}}}} \right)}}} \right)}^{\frac{1}{{1.996}}}}}} - 0.1273} \right] - \frac{{{N_{{\rm{bi}}}}{C_{{\rm{eff}}}}\Delta p}}{{{B_{\rm{w}}}}} - F} \right\} \end{array} $ | (27) |
利用式(26)和式(27)可以计算不同累积水油比、不同地层压力和不同含水率下所需的阶段注采比,历史计算结果如表 3所示,可以看出,方法一与方法二的计算结果均与实际注采比都比较接近,因此,对该实例油藏在实际注采比预测应用中可取两种方法计算结果的平均值。
| 表3 实例层生产动态数据阶段注采比计算结果 Table 3 Calculation results of injection—production ratio for the example formation |
该油藏2013年按照方法一和方法二计算取平均值,计算出合理注采比为0.551 0,以此为依据开展了实际的注水配注工作,实际配注结果其注采比为0.563 0,从2013年1月到8月阶段累积产油量达到2.988$\times$10$^4$ t,到8月31日油藏含水率为0.879 4,压力下降了0.13 MPa,应用结果表明该方法指导生产配注取得了较好的效果。
在油田实际生产应用过程中,当含水上升后,一般都要进行注采结构调整等措施以达到稳油控水的目的,而注采结构调整后的累积注入量和累积产油量间的关系式、累积产油量与含水率关系式及水驱特征曲线将随之发生改变,因此,若油藏注采结构发生过调整,则应根据油藏的实际变化情况采取分阶段拟合$C_1$、$D$等参数值,以获取不同阶段的注采比计算公式。若油藏注水时间越长,累积产量与含水饱和度关系式等生产数据回归的数据点越多,注采比计算结果的可靠性越强。研究的两种阶段注采比计算方法对于裂缝性封闭油藏是否适用,还有待实例验证。此外,文中在推导中所用的公式要求累积产量随前缘含水饱和度上升而上升,因此,研究的方法不适用于无水采油期。
3 结 论(1)获得了两种新的阶段注采比计算关系式,可综合考虑油藏压力、含水率、累积水油比的影响,还包含了储层厚度、孔隙度、含油面积等基本油藏参数,可用于封闭油藏注水开发的阶段注采比计算。
(2)实例应用表明研究的两种阶段注采比计算方法对单一孔隙介质的油藏计算结果与实际情况吻合性较好,但对于裂缝性封闭油藏是否适用,还有待检验。
(3)研究的两种阶段注采比计算方法不适用于无水采油期,油藏注水时间越长,生产数据回归的数据点越多,注采比计算结果的可靠性越强。
符 号 说 明$W_{\rm{i}}$——累积注水量,$\times$10$^4$ m$^3$;$N_{\rm{p}}$——累积产油量,$\times$10$^4$ m$^3$;${Q_{\rm{wi}}}$——注水量,$\times$10$^4$ m$^3$;$\zeta$——中间代换变量,$\zeta$=1 m$^{-3}$;${Q_{\rm{o}}}$——产油量,$\times$10$^4$ m$^3$;${B_{\rm{o}}}$——原油体积系数,无因次;$N_{\rm{bi}}$——原始地质储量,$\times$10$^4$ m$^3$;$C_{\rm{eff}}$——地层岩石和流体有效压缩系数,MPa$^{-1}$;$\Delta p$——地层压力降,MPa;$p$——地层压力,MPa;${B_{\rm{w}}}$——地层水的体积系数,无因次;$W_{\rm{p}}$——累积产水量,$\times$10$^4$ m$^3$;${B_{{\rm{oi}}}}$——原始原油体积系数,无因次;$C_{\rm{p}}$——岩石压缩系数,MPa$^{-1}$;${S_{\rm{wc}}}$——束缚水饱和度,无因次;$C_{\rm{w}}$——地层水压缩系数,MPa$^{-1}$;$R_{\rm{wo}}$——累积水油比,无因次;$R_{\rm{IP}}$——阶段注采比,无因次;${Q_{\rm{L}}}$——产液量,$\times$10$^4$ m$^3$;$f_{\rm{w}}$——地面含水率,无因次;$R$——采出程度,无因次;$A$——储层含油面积,km$^2$;}$h$——储层有效厚度,m;$\phi$——孔隙度,%;${S_{\rm{w}}}$——含水饱和度,无因次;${S_{\rm{or}}}$——残余油饱和度,无因次;${S_{\rm{wi}}}$——原始含水饱和度,小数;${Q_{\rm{w}}}$——产水量,$\times$10$^4$ m$^3$;${\mu _{\rm{w}}}$——地层水黏度,mPa$\cdot$s;${\mu _{\rm{o}}}$——原油黏度,mPa$\cdot$s;$K_{\rm{ro}}$——油相相对渗透率,无因次;$K_{\rm{rw}}$——水相相对渗透率,无因次;$F$,$\alpha$,$\beta$,$C_1$,$D$,$C_2$,$n$——拟合常数,无因次。
| [1] | 牟汉兵, 闫海霞, 夏廷仪, 等. 张店油田精细注水实践与认识[J]. 石油天然气学报, 2010, 32 (2) : 345–348. |
| [2] |
轩玲玲, 任利斌, 刘锋, 等. 油田注水前后储层特征变化规律研究-以冀东高尚堡油田沙三段2+3亚段为例[J].
岩性油气藏, 2010, 22 (4) : 116–119.
Xuan Lingling, Ren Libin, Liu Feng, et al. Reservoir feature variation rule before and after water injection:An example from the second and third sub-members of the third member of Shahejie Formation in Gaoshangpu Oilfield of Jidong[J]. Lithologic Reservoirs, 2010, 22 (4) : 116–119. |
| [3] |
上官永亮, 赵庆东, 宋杰, 等. 注水井合理配注方法研究[J].
大庆石油地质与开发, 2003, 22 (3) : 40–42.
Shangguan Yongliang, Zhao Qingdong, Song Jie, et al. Research of reasonable water injection method[J]. Petroleum Geology & Oilfield Development in Daqing, 2003, 22 (3) : 40–42. |
| [4] | 洪承燮, 季华生, 王晓虹. 注采动态分析及定量配注方法研究[J]. 石油勘探与开发, 1992, 19 (2) : 56–62. |
| [5] | Lerma M K. Analytical method to predict waterflood performance[C]. SPE 83511, 2003. |
| [6] | Lee K H, Ortega A, Nejad A M. A method for characterization of flow units between injection-production wells using performance data[C]. SPE 114222, 2008. |
| [7] | 吴琼, 张文忠, 张春强. 应用逻辑斯蒂旋回模型预测注水量的方法研究[J]. 特种油气藏, 2011, 18 (1) : 67–69. |
| [8] |
杨延明, 苏建栋, 马培申. 水驱油田不同含水时期合理注水量计算方法[J].
石油勘探与开发, 1998, 25 (3) : 69–71.
Yang Yanming, Su Jiandong, Ma Peishen. Reasonable water injection rate calculation for water flooding reservoirs at different water-cut stages[J]. Petroleum Exploration and Development, 1998, 25 (3) : 69–71. |
| [9] |
陈元千, 胡建国, 张栋杰. Logistic模型的推导及自回归方法[J].
新疆石油地质, 1996, 17 (2) : 150–155.
Chen Yuanqian, Hu Jianguo, Zhang Dongjie. Derivation of logistic model and its self-regression method[J]. Xinjiang Petroleum Geology, 1996, 17 (2) : 150–155. |
| [10] | 杨康佑, 范尚炯, 陈元千, 等. 石油及天然气储量计算方法. 北京:石油工业出版社[M]. 1998 : 186 -187. |
| [11] |
蒋明, 宋富霞. 利用配产量确定配注量的一种方法[J].
试采技术, 1998, 19 (3) : 24–27.
Jiang Ming, Song Fuxia. A method of using match output to determine the volume of injection[J]. Producing Test Technology, 1998, 19 (3) : 24–27. |
| [12] | 黄李荣. 注水开发油田单井配注方法研究[D]. 成都:西南石油大学, 2006. |
| [13] |
屈斌学. 油藏注采比计算方法综述[J].
石油化工应用, 2009, 28 (5) : 7–10.
Qu Binxue. Reservoir injection-production ratio calculation method[J]. Petrochemical Industry Application, 2009, 28 (5) : 7–10. |
| [14] |
钟德康. 注采比变化规律及矿场应用[J].
石油勘探与开发, 1997, 24 (6) : 65–69.
Zhong Dekang. The variation rule of injection-production ratio and the field application[J]. Petroleum Exploration and Development, 1997, 24 (6) : 65–69. |
 2014, Vol. 36
2014, Vol. 36

