2. 中国石油华北油田公司, 河北 任丘 062552
2. North China Oilfield Company, PetroChina, Renqiu, Hebei 062552, China
水力压裂技术是页岩气等致密气藏开发的核心技术之一,统计表明,90%的页岩气井完井后需要人工压裂才能获得产量[1]。而清水压裂以其成本低、对地层伤害小等优点成为页岩气藏(尤其是较高压力、较大埋深的气藏)的主要压裂技术[2]。清水压裂时因压裂液黏度小、注入量大等因素导致支撑剂在裂缝内的输送沉降方式与其他压裂过程明显不同,湍流、颗粒间的碰撞、裂缝壁面等此时成为重要的影响因素[3]。传统支撑剂沉降计算方法因没有考虑到流固双向、固固间的耦合作用而难以准确描述清水压裂中支撑剂的输送沉降行为[4],为了能弄清楚支撑剂在清水压裂过程中的沉降机理,有必要引入新的思想来研究该问题。
由于能够同时求解液固两相的流动规律,多相流计算流体力学方法(Computational Fluid Mechanics,CFD)为更深入地研究支撑剂沉降问题提供了新的思路。如Patankar N A等对颗粒在牛顿及非牛顿流体中的自由沉降采用基于任意欧拉-拉格朗日描述的直接数值模拟方法进行了模拟,结果展示了颗粒间沉降过程中相互干扰的行为及影响颗粒沉降的因素。对牛顿流体平面泊肃叶流中颗粒床扩展进行了直接数值模拟,以无量纲参数群建立了颗粒的举升准则。依据模拟结果对STIM-LAB的支撑剂沉降实验成果进行处理,分别给出了计算支撑剂输送中缝宽与无砂区及悬砂区高度比值的幂函数和双幂函数经验公式[5]。Eskin D等基于颗粒动力学理论研究了水平裂缝中支撑剂颗粒的迁移和垂直裂缝支撑剂的沉降动力学行为[6]。在忽略裂缝扩展、压裂液滤失等影响因素下,Tsai K等研究了页岩气藏清水压裂中支撑剂沉降行为,对压裂液流动采用大涡模型进行流场分析,而支撑剂则采用拉格朗日法进行跟踪。压裂液和支撑剂颗粒之间采用Wen-Yu的阻力模型耦合,颗粒之间考虑主应力,颗粒壁面之间作用通过回归系数考虑,计算结果展示了流量和支撑剂参数对支撑剂沉降过程及铺设规律的影响[7]。
欧拉-欧拉两流体多相流数值方法在近30年来取得了长足的进步。文献[8]将固相流动控制方程从单分散体系扩展到多分散体系。为了提高有限网格下的模拟精度,Wang W等发展了能量最小化多尺度流固耦合阻力模型,该模型能模拟两相流中的多尺度流动结构[9]。Srivastava A等发展了稠密固相流中的固相摩擦应力模型,模型考虑了固相含量超过临界浓度时的作用力[10]。Benyahia S评价了Jenkins-Louge和Johnson-Jackson固相壁面边界条件,指出两种边界条件的适用范围[11]。根据文献[12]对流化床和管道泥浆流应用看出,两流体多相流模型的模拟结果与实验结果符合度高。
相对于文献[5-7]所采用的CFD方法,欧拉-欧拉两流体模型具有研究成果多、计算量小等优点,可以预见,欧拉-欧拉两流体模型是未来工程多相流问题计算的优先选择[13]。本文探讨采用两流体模型模拟平板裂缝中清水携带支撑剂输运沉降行为。
1 液固多相流模型式(1)~式(4)给出了压裂液相和固相的质量守恒、动量守恒方程。固相的质量、动量及颗粒温度的输运方程通过颗粒动理学理论获得[10-11, 14]。
液相和固相的连续性方程分别为
| $ \dfrac{\partial }{{\partial t}}\left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{{\textbf{v}}_{\rm{l}}}} \right) = 0 $ | (1) |
| $ \dfrac{\partial }{{\partial t}}\left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{{\textbf{v}}_{\rm{s}}}} \right) = 0 $ | (2) |
式中:$t$——时间,s;${\alpha}$——体积分数,无因次;${\rho}$——密度,kg/m$^3$;${{\textbf{v}}}$——速度,m/s;下标l,s——液相,固相。
液相和固相的动量守恒方程分别为
| $ {\frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{{\bf{v}}_{\rm{l}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{{\bf{v}}_{\rm{l}}}{{\bf{v}}_{\rm{l}}}} \right) = - {\alpha _{\rm{l}}}\nabla {p_{\rm{l}}} + \nabla \cdot {\tau _1} + {\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\rm{g}} + \beta \left( {{{\bf{v}}_{\rm{s}}} - {{\bf{v}}_{\rm{l}}}} \right)} $ | (3) |
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{{\bf{v}}_{\rm{s}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}{{\bf{v}}_{\rm{s}}}{{\bf{v}}_{\rm{s}}}} \right) = - {\alpha _{\rm{s}}}\nabla {p_{\rm{s}}} + \nabla \cdot {\tau _{\rm{s}}} + {\alpha _{\rm{s}}}{\rho _{\rm{s}}}{\rm{g}} + \beta \left( {{{\bf{v}}_{\rm{l}}} - {{\bf{v}}_{\rm{s}}}} \right) $ | (4) |
式中:$p$——分压,Pa;${\textbf{τ}}$——剪切应力张量,Pa;$\rm{g}$——重力加速度,g = 9.8~m/s$^2$;$\beta$——相间动量交换系数,kg/(m$^3{\cdot}$s)。
固相颗粒温度正比于颗粒随机脉动动能,其输运方程为
| $ \frac{3}{2}{\rho _{\rm{s}}}\left[{\frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{s}}}{\Theta _{\rm{s}}}} \right) + \nabla \cdot \left( {{\alpha _{\rm{s}}}{{\bf{v}}_{\rm{s}}}{\Theta _{\rm{s}}}} \right)} \right] = \nabla \cdot \left( {{\kappa _{\rm{s}}}\nabla {\Theta _{\rm{s}}}} \right) + {\tau _{\rm{s}}}:\nabla {{\bf{v}}_{\rm{s}}} - {J_{\rm{s}}} + {\prod _\Theta } $ | (5) |
式中:$\varTheta_{\rm{s}}$——颗粒拟温度,m$^2$/s$^2$;$\kappa_{\rm{s}}$——颗粒能量传导系数,kg/(m$\cdot$s);$J_{\rm{s}}$——非弹性碰撞导致的能量耗散,kg/(m$\cdot$s$^3$);${\varPi _{\rm{\Theta }}}$——因流体黏性阻尼而产生能量耗散,kg/(m$\cdot$s$^3$)。
湍流的影响通过$k$-$\varepsilon$湍流模型加以考虑,湍动能$k$方程和耗散率$\varepsilon$方程分别为
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}k} \right) + \nabla \cdot \left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{{\bf{v}}_{\rm{l}}}k} \right) = \nabla \cdot \left( {{\alpha _{\rm{l}}}\frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}\nabla k} \right) + {G_{{\rm{k}},{\rm{l}}}} + {\prod _{\rm{k}}} - {\alpha _{\rm{l}}}{\rho _{\rm{l}}}\varepsilon $ | (6) |
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}\varepsilon } \right) + \nabla \cdot \left( {{\alpha _{\rm{l}}}{\rho _{\rm{l}}}{{\bf{v}}_{\rm{l}}}\varepsilon } \right) = \nabla \cdot \left( {\frac{{{\alpha _{\rm{l}}}{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}\nabla \varepsilon } \right) + {\alpha _{\rm{l}}}\frac{\varepsilon }{k}\left( {{C_{{\rm{1}}\varepsilon }}{G_{{\rm{k}},{\rm{l}}}} - {C_{{\rm{2}}\varepsilon }}{\rho _{\rm{l}}}\varepsilon } \right) + {\prod _\varepsilon } $ | (7) |
式中:$k$——流体相的湍动能,m$^2$/s$^2$ ;${\mu}_{\rm{t}}$——湍流黏性系数,Pa$\cdot$s;$\sigma_{\rm{k}}$——湍动能对应的普朗特数,无因次,取$\sigma_{\rm{k}}=1.0$;${G_{{\rm{k,l}}}}$——湍动能的产生项,kg/(m$\cdot$s$^3$);${\varPi _{\rm{k}}}$,${\varPi _{\rm{\varepsilon}}}$——液固两相间湍流交换项,kg/(m$\cdot$s$^3$);${\varepsilon}$——湍流耗散率,m$^2$/s$^3$;$\sigma_{\varepsilon}$——湍动耗散率对应的普朗特数,无因次,取$\sigma_{\varepsilon}=1.3$;${{C}_{1\varepsilon }}$,$C_{2\varepsilon}$%,${{C}_{3\varepsilon }}$——经验常数,无因次,取${{C}_{1\varepsilon }}$=1.44、${C_{2\varepsilon }}$=1.92。
1.1 本构方程上述控制方程需要本构关系加以封闭,下面给出本文所采用的本构关系。采用Gidaspow模型,液固两相间的动量交换系数$\beta$为:
当${\alpha _{\rm{l}}} \geqslant 0.8$时
| $ \beta =\dfrac{3}{4}{C_{\rm{D}}}\dfrac{{{\rho _{\rm{l}}}{\alpha _{\rm{l}}}{\alpha _{\rm{s}}}\left| {{{{\textbf{v}}}_{\rm{l}}} - {{{\textbf{v}}}_{\rm{s}}}} \right|}}{{{d_s}}}\alpha _{\rm{l}}^{ - {\rm{2}}{\rm{.65}}} $ | (8) |
| $ \beta =\dfrac{{150{\alpha _{\rm{s}}}\left( {1 - {\alpha _{\rm{l}}}} \right){\mu _{\rm{l}}}}}{{{\alpha _{\rm{l}}}d_{\rm{s}}^{\rm{2}}}} + \dfrac{{1.75{\rho _{\rm{l}}}{\alpha _{\rm{s}}}\left| {{{{\textbf{v}}}_{\rm{l}}} - {{{\textbf{v}}}_{\rm{s}}}} \right|}}{{{d_{\rm{s}}}}} $ | (9) |
其中
| $ {C_{\rm{D}}} = \left\{ \begin{array}{l} \frac{{24}}{{{\rm{ }}R{e_{\rm{s}}}}}\left[{1 + 0.15{{\left( {{\rm{ }}R{e_{\rm{s}}}} \right)}^{0.687}}} \right]{\rm{ }}R{e_{\rm{s}}} < 1000\\ 0.44{\rm{ }}R{e_{\rm{s}}} \ge 1000 \end{array} \right. $ |
| $ {{\mathop{ Re}\nolimits} _{\rm{s}}} = \dfrac{{{\rho _{\rm{l}}}{d_{\rm{s}}}{\varepsilon _{\rm{l}}}\left| {{{{\textbf{v}}}_{\rm{s}}} - {{{\textbf{v}}}_{\rm{l}}}} \right|}}{{{\mu _{\rm{l}}}}} $ |
式中:$C_{\rm{D}}$——相间动量交换阻力系数,无因次;$d_{\rm{s}}$——固相颗粒直径,m;${\mu}_{\rm{l}}$————液相黏度,Pa$\cdot$s;${{\mathop{ Re}\nolimits} _{\rm{s}}}$——以相间滑移速度定义的雷诺数,无因次。
液相、固相剪切应力分别为
| $ {\tau _{\rm{l}}} = 2{\alpha _{\rm{l}}}{\mu _{\rm{l}}}{{\bf{S}}_{\rm{l}}} $ | (10) |
| $ {\tau _{\rm{s}}} = \left[{\eta {\mu _{\rm{b}}}\nabla \cdot {{\bf{v}}_{\rm{s}}} - \left( {{p_{\rm{s}}} + {p_{\rm{f}}}} \right)} \right]{\bf{I}} + 2\left( {{\mu _{\rm{s}}} + {\mu _{\rm{f}}}} \right){{\bf{S}}_{\rm{s}}} $ | (11) |
式中:${{\textbf{S}}_{\rm{l}}}$,${{\textbf{S}}_{\rm{s}}}$——液相、固相应变张量,s$^{-1}$;$p_{\rm{s}}$——固相压力,Pa;$p_{\rm{f}}$——固相摩擦压力,Pa;${\mu}_{\rm{b}}$——固相体积黏性系数,Pa$\cdot$s;${\mu}_{\rm{s}}$——固相剪切黏性系数,Pa$\cdot$s;${\mu}_{\rm{f}}$——摩擦黏性系数,Pa$\cdot$s;${\textbf{I}}$——二阶单位张量,无因次;$\eta$——系数,无因次,$\eta= \left( {1 + e} \right)/2$;$e$——颗粒间碰撞的回归系数,取0.9。
液相、固相应变张量为
| $ {{\textbf{S}}_{\rm{l}}} = \dfrac{1}{2}\left[{\nabla {{{\textbf{v}}}_{\rm{l}}} + {{\left( {\nabla \cdot {{{\textbf{v}}}_{\rm{l}}}} \right)}^{\rm{T}}}} \right] - \dfrac{1}{3}\left( {\nabla \cdot {{{\textbf{v}}}_{\rm{l}}}} \right){\textbf{I}} $ | (12) |
| $ {{\textbf{S}}_{\rm{s}}} = \dfrac{1}{2}\left[{\nabla {{{\textbf{v}}}_{\rm{s}}} + {{\left( {\nabla {{{\textbf{v}}}_{\rm{s}}}} \right)}^{\rm{T}}}} \right] - \dfrac{1}{3}\left( {\nabla \cdot {{{\textbf{v}}}_{\rm{s}}}} \right){\textbf{I}} $ | (13) |
颗粒接触径向分布函数
| $ {g_0} = \dfrac{{1 - 0.5{\alpha _{\rm{s}}}}}{{{{\left( {1 - {\alpha _{\rm{s}}}} \right)}^3}}} $ | (14) |
固相剪切黏性系数为
| $ {\mu _{\rm{s}}} = \left( {\frac{{2 + c}}{3}} \right) \cdot \frac{3}{5}\eta {\mu _{\rm{b}}} + \left( {\frac{{2 + c}}{3}} \right) \cdot \frac{{{\mu ^*}}}{{{g_0}\eta \left( {2 - \eta } \right)}} \cdot \left( {1 + \frac{8}{5}\eta {\alpha _{\rm{s}}}{g_0}} \right)\left[{1 + \frac{8}{5}\eta \left( {3\eta - 2} \right){\alpha _{\rm{s}}}{g_0}} \right] $ | (15) |
| $ {\mu ^*} = \mu {\left[{1 + \frac{{2\beta \mu }}{{{{\left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}} \right)}^2}{g_0}{\Theta _{\rm{s}}}}}} \right]^{ - 1}} $ | (16) |
| $ \mu = \frac{{5{\rho _{\rm{s}}}{d_{\rm{s}}}\sqrt {{\Theta _{\rm{s}}}\pi } }}{{96}} $ | (17) |
| $ {\mu _{\rm{b}}} = \frac{{256}}{{5\pi }}\mu \alpha _{\rm{s}}^2{g_0} $ | (18) |
式中:$c$——固相黏性常数,取值1.6;${\mu}^{*}$——考虑颗粒间流体影响的固相黏性系数,Pa$\cdot$s;${\mu}$——稀疏固相黏性系数,Pa$\cdot$s。
固相脉动能量的传导系数为
| $ \begin{array}{l} {\kappa _{\rm{s}}} = \left( {1 + \frac{{12}}{5}\eta {\alpha _{\rm{s}}}{g_0}} \right)\left[{1 + \frac{{12}}{5}{\eta ^2}\left( {4\eta - 3} \right){\alpha _{\rm{s}}}{g_0}} \right] \cdot \\ \left( {\frac{{{\kappa ^*}}}{{{g_0}}}} \right) + \frac{{64}}{{25\pi }}\left( {41 - 33\eta } \right){\eta ^2}{\left( {{\alpha _{\rm{s}}}{g_0}} \right)^2}\left( {\frac{{{\kappa ^*}}}{{{g_0}}}} \right) \end{array} $ | (19) |
| $ {\kappa ^*} = \kappa {\left[{1 + \frac{{6\beta \kappa }}{{5{{\left( {{\alpha _{\rm{s}}}{\rho _{\rm{s}}}} \right)}^2}{g_0}{\Theta _{\rm{s}}}}}} \right]^{ - 1}} $ | (20) |
| $ \kappa = \frac{{75{\rho _{\rm{s}}}{d_{\rm{s}}}\sqrt {\pi {\Theta _s}} }}{{48\eta \left( {41 - 33\eta } \right)}} $ | (21) |
式中:${\kappa ^ * }$——考虑颗粒间流体作用的固相能量传导系数,kg/(m$\cdot$s);${\kappa }$——稀疏固相能量传导系数,kg/(m$\cdot$s)。
固相摩擦压力和黏性系数分别为
| $ \frac{{{p_{\rm{f}}}}}{{{p_{\rm{c}}}}} = {\left( {1 - \frac{{\nabla \cdot {{\bf{v}}_{\rm{s}}}}}{{n\sqrt 2 \sin \delta \sqrt {{{\bf{S}}_{\rm{s}}}:{{\bf{S}}_{\rm{s}}} + {\Theta _{\rm{s}}}/d_{\rm{p}}^2} }}} \right)^{n - {\rm{1}}}} $ | (22) |
| $ {\mu _{\rm{f}}} = \frac{{{p_{\rm{f}}}\sin \delta }}{{\sqrt 2 \sqrt {{{\bf{S}}_{\rm{s}}}:{{\bf{S}}_{\rm{s}}} + {\Theta _{\rm{s}}}/d_{\rm{p}}^2} }} \cdot \left[{n - \left( {n - 1} \right){{\left( {\frac{{{p_{\rm{f}}}}}{{{p_{\rm{c}}}}}} \right)}^{\frac{1}{{n - 1}}}}} \right] $ | (23) |
其中
| $ {p_{\rm{c}}} = \left\{ \begin{array}{l} {10^{25}}{\left( {{\alpha _{\rm{s}}} - \alpha _{\rm{s}}^{\max }} \right)^{10}}{\rm{ }}{\alpha _{\rm{s}}} > \alpha _{\rm{s}}^{\max }\\ {F_{\rm{r}}}\frac{{{{\left( {{\alpha _{\rm{s}}} - \alpha _{\rm{s}}^{\min }} \right)}^{{{\rm{r}}^\prime }}}}}{{{{\left( {\alpha _{\rm{s}}^{\max } - {\alpha _{\rm{s}}}} \right)}^{{{\rm{s}}^\prime }}}}}{\rm{ }}\alpha _{\rm{s}}^{\max }{\alpha _{\rm{s}}} > \alpha _{\rm{s}}^{\min }\\ 0{\rm{ }}{\alpha _{\rm{s}}}\alpha _{\rm{s}}^{\min } \end{array} \right.\ $ |
| $ n = \left\{ \begin{array}{l} \frac{{\sqrt 3 }}{2}\sin \delta {\rm{ }}\nabla \cdot {{\bf{v}}_{\rm{s}}}0\\ 1.03{\rm{ }}\nabla \cdot {{\bf{v}}_{\rm{s}}} < 0 \end{array} \right. $ |
式中:$p_{\rm{c}}$——临界固相压力,Pa;$F_{\rm{r}}$——摩擦模型系数,无因次,取0.05;r$'$,s$'$——常数,无因次,分别取值2和5;$\delta$——固相间内摩擦角,rad,取$\pi $/6;$\alpha _{\rm{s}}^{\max }$——颗粒最大堆积浓度,%,取63%;$\alpha _{\rm{s}}^{\min }$——产生临界压力的固相体积分数,%,取50%。
湍流动能的产生项为
| $ {G_{{\rm{k}},{\rm{l}}}} = \varepsilon {\mu _{\rm{t}}}\left( {\nabla {{\bf{v}}_{\rm{l}}} + \nabla {\bf{v}}_{\rm{l}}^{\rm{T}}} \right):\nabla {{\bf{v}}_{\rm{l}}} $ | (24) |
固相脉动能量的碰撞耗散及黏性阻尼项的经验公式为
| $ {J_{\rm{s}}} = \frac{{48}}{{\sqrt {{\rm{ }}\pi } }}\eta \left( {1 - \eta } \right)\frac{{{\rho _{\rm{s}}}\alpha _{\rm{s}}^2{g_0}}}{{{d_{\rm{s}}}}}\Theta _{\rm{s}}^{3/2} $ | (25) |
| $ {\prod _\Theta } = - 3\beta {\Theta _{\rm{s}}} + 81\frac{{{\alpha _{\rm{s}}}\mu _{\rm{l}}^{\rm{2}}{{\left| {{{\bf{v}}_{\rm{l}}} - {{\bf{v}}_{\rm{s}}}} \right|}^2}}}{{{g_0}d_{\rm{s}}^3{\rho _{\rm{s}}}\sqrt {\pi {\Theta _{\rm{s}}}} }} $ | (26) |
两相湍流作用项的经验公式为
| $ {\prod _{\rm{k}}} = \beta \left( {3{\Theta _{\rm{s}}} - 2k} \right),{\prod _\varepsilon } = 0 $ | (27) |
进口边界条件给出液固两相的速度和体积分数,出口边界条件指定压力(标准大气压)。
固壁处指定液相法向和切向速度为零(非滑移边界条件)。固相在固壁处的法向速度为零,切向速度和颗粒温度根据Johnson-Jackson模型[11}计算
| $ \frac{{{{\bf{v}}_{{\rm{sl}}}}}}{{\left| {{{\bf{v}}_{{\rm{sl}}}}} \right|}} \cdot \left( {{\tau _{\rm{k}}} + {\tau _{\rm{f}}}} \right) \cdot {\bf{w}} + \frac{{\phi {\rm{ }}\pi {\rho _{\rm{s}}}{\alpha _{\rm{s}}}{g_0}\sqrt {{\Theta _{\rm{s}}}} }}{{2\sqrt 3 \alpha _{\rm{s}}^{\max }}}{{\bf{v}}_{{\rm{sl}}}} + \left( {{\bf{w}} \cdot {\tau _{\rm{f}}} \cdot {\bf{w}}} \right)\tan {\delta _{\rm{w}}} = 0 $ | (28) |
| $ {\kappa _{\rm{s}}}\frac{{\partial {\Theta _{\rm{s}}}}}{{\partial x}} = \frac{{\phi {\rm{ }}\pi \left| {{{\bf{v}}_{{\rm{sl}}}}} \right|{\rho _{\rm{s}}}{\alpha _{\rm{s}}}{g_0}\sqrt {{\Theta _{\rm{s}}}} }}{{2\sqrt 3 \alpha _{\rm{s}}^{\max }}} - [9pt]\frac{{\sqrt 3 \pi {\rho _{\rm{s}}}{\alpha _{\rm{s}}}{g_0}\left( {1 - e_{\rm{w}}^2} \right)\sqrt {{\Theta _{\rm{s}}}} }}{{4\alpha _{\rm{s}}^{\max }}}{\Theta _{\rm{s}}} $ | (29) |
式中:${{{\textbf{v}}}_{{\rm{sl}}}}$——固相壁面间的滑移速度矢量,m/s;${{\textbf{τ}}}_{\rm{k}}$,${{\textbf{τ}}}_{\rm{f}}$——固相动力学碰撞和摩擦在壁面产生的剪切应力张量,Pa;${{\textbf{w}}}$——壁面向内的法向矢量;$\phi$——反射系数,无因次,取0.001;$\delta _{\rm{w}}$——壁面摩擦角,rad,取$\pi $/10;$e_{\rm{w}}$——颗粒和壁面碰撞的恢复系数,取0.9。
2 几何模型及求解策略模拟对象为文献[15]中开展支撑剂沉降实验的平板裂缝模型,数值模拟裂缝大小与其相同(3~000~mm$\times$400~mm$\times$10~mm)。模拟时在裂缝左侧可设3种进口位置(中部指位于缝高中心位置,底部指距底面20~mm处,顶部指距顶面20~mm处),进口大小均为40~mm$\times$10~mm,裂缝右端均布8个相同大小(20~mm$\times$10~mm)的出口。
由于裂缝模型形状规则,数值计算网格划分时对长高宽方向进行均分。网格数目在长度方向上为150个、高度方向为40个而宽度方向为6个,最终裂缝采用20.00~mm$\times$10.00~mm×1.67~mm的正六面体进行网格划分。数值模拟时压裂液为清水,与实验相同,支撑剂颗粒假设为球形。
上述控制方程采用有限体积法求解,离散格式为一阶上风格式,收敛标准为各项残差小于10$^{-4}$。分析模拟结果时均取缝宽方向位于中心的平面进行。
3 结果及讨论 3.1 与实验比对Liu Yajun在文献中指出当砂浆(水和支撑剂组成的混合物)由裂缝中部注入时,砂丘的形成包含了3个阶段,如图 1所示[15]。其中,图 1a为第一阶段,支撑剂在射流的滞止点位置附近因重力而沉降至缝底形成砂丘;图 1b为第二阶段,砂丘不断增高改变了射流形态,在距进口一定距离处支撑剂床形成一个高峰,而进口附近形成一个凹槽;图 1c为第三阶段,在本阶段中砂丘已达到平衡高度,进一步注入的支撑剂只能在砂丘背面发生沉降和运移。
由于Liu Yajun在文献中并没有说明图 1的注入流量及支撑剂的浓度,本文选择中部注入且速度3~m/s,颗径1~mm浓度为20%的条件%作为对照组来进行对比(图 2)。图 2a为注入时间为5~s形成的砂丘,砂丘距进口距离约85~cm,对应图 1a中的砂丘形成初级阶段;图 2b可对应砂丘形成的第二阶段,砂丘高度不断增大;图 2c对应第三阶段的砂丘达到平衡高度状态;图 2d则表示达到平衡高度后支撑剂床不断延伸的过程。
 |
| 图1 砂丘形成的3个阶段(流向由右向左) Fig. 1 3 stages of proppant bed buildup(flow from right to left) |
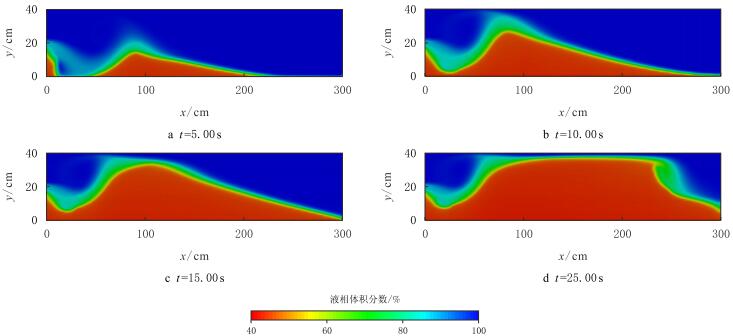 |
| 图2 中部注入时液相体积分数分布 Fig. 2 Liquid volume fraction at middle inlet boundary |
从对应图 2的水流速度场分布(图 3)看,自入口进入后的砂浆混合物迅速发生对流沉降行为(因混合物密度高于下部液体密度引起),在距入口约85~cm处支撑剂颗粒堆积形成砂丘,而水流则自砂丘上方减速流过(图 3a)。砂丘的形成不断抬升砂浆射流,使裂缝进口附近逐渐堆积部分支撑剂,但由于平衡高度没有达到,砂丘的高度不断增加,而绕过其的水流速度不断增加(图 3b)。在图 3c中,当砂丘顶端和裂缝顶部间隙减小到一定值时,该区域内水流携带的支撑剂颗粒沉降数目和砂丘中颗粒被流化的数目相等,这时砂丘的平衡高度形成,颗粒只能运移到砂丘背面发生沉降。由图 2d中可以看出,随着支撑剂床的不断扩展,在床顶部形成一条混合物输运的通道。
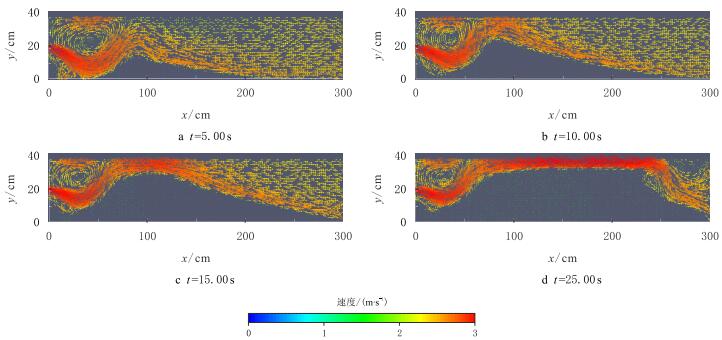 |
| 图3 中部注入时水流速度场 Fig. 3 Liquid velocity distribution at middle inlet boundary |
图 4,图 5为砂浆射流速度分别为2,4~m/s条件下的液相体积分数,图 4和图 5中所选时间点与图 2(射流速度3~m/s)对应(以注入支撑剂体积相同为依据)。
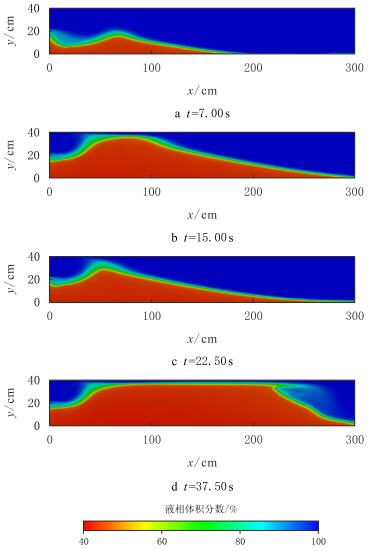 |
| 图4 进口液相速度为2~m/s时液相体积分数分布 Fig. 4 Liquid volume fraction at 2~m/s |
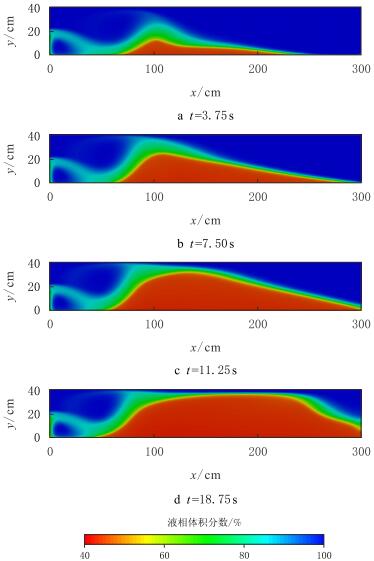 |
| 图5 进口液相速度为4~m/s时液相体积分数分布 Fig. 5 Liquid volume fraction at 4~m/s |
在速度为2~m/s时,砂浆混合物进入裂缝后迅速沉降至距进口约50~cm位置,支撑剂颗粒继续向前运动至约70~cm处停止形成砂丘。随着砂丘高度不断增加,射流轨迹被改变,进口至砂丘中间区域被逐渐颗粒填充(图 4a及图 4b)。由于进口附近区域被支撑剂填充,图 4c虽然注入与图 2c相同的支撑剂量,但支撑剂床并没有达到平衡高度。图 4d为进一步注入混合物达到平衡高度时,支撑剂床扩展的过程,此时平衡高度较速度3~m/s稍小。
射流速度为4~m/s时,砂浆在进入裂缝后同样迅速沉降至缝底(距进口约70~cm),但此时混合物的速度仍有足够的动能向前运动,至距进口约105~cm处支撑剂颗粒无法再被向前推动而停止(图 5a)。此后,砂丘高度不断增长,同时射流绕过砂丘流走(图 5b)。当砂丘高度平衡高度达到后(图 5c),图 5d中的支撑剂床扩展过程与前两种速度条件下并无明显不同。
对比不同速度下的两图可看出,除支撑剂沉降距离不同外,较高的射流速度将会导致进口附近无支撑剂颗粒沉降。此外,不同砂浆速度对支撑剂的流化能力不同,平衡高度随速度增大不断增大。
3.3 进口位置的影响在底部入口条件下,砂浆混合物射流沿裂缝底部前进,因此在进口附近不可能发生支撑剂的沉降。随着射流向上侧扩散,其速度减小至无法推动支撑剂向前运动,则在距进口约100~cm处形成沙丘(图 6a)。图 6b中沙丘的高度不断增加,直至达到图 6c所示的平衡高度,其后支撑剂床不断扩展(图 6d)。可以看出,底部进口条件下,裂缝进口附近会形成大片的无支撑区域,区域的大小跟砂浆射流的速度有关。
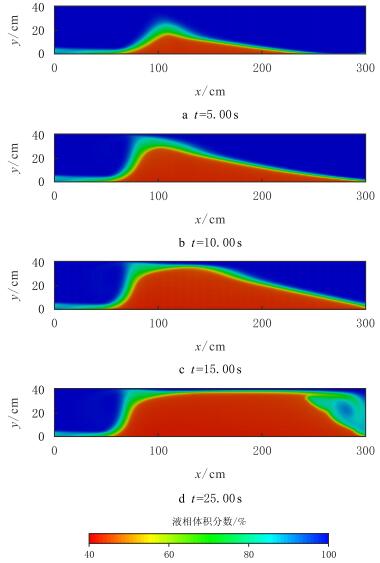 |
| 图6 进口位于底部时液相体积分布 Fig. 6 Liquid volume fraction at bottom inlet boundary |
图 7中砂浆射流自顶部进入裂缝后在距进口约125~cm位置开始形成砂丘,而受射流回流的影响,进口附近出现另一个砂丘(图 7a)。随着砂丘高度增加,射流轨迹被抬升,两砂丘中部的区域同样被支撑剂所填满(图 7b)。其后,出现了自进口位置开始的支撑剂床整体不断升高的过程(图 7c),在此过程中,支撑剂沉降行为使射流出现强烈的不稳定动力学过程,加大了对支撑剂沉降输运沉降过程认识的难度。从图 7d中看出,这种工作条件下近井附近区域支撑剂基本铺设完整,其后才不断向后扩展。
对比3种条件下(图 2,图 6,图 7)支撑剂分布可知,进口位置对近井位置裂缝内支撑剂的铺设规律有重要影响,进而极大地影响整个裂缝的渗透率。
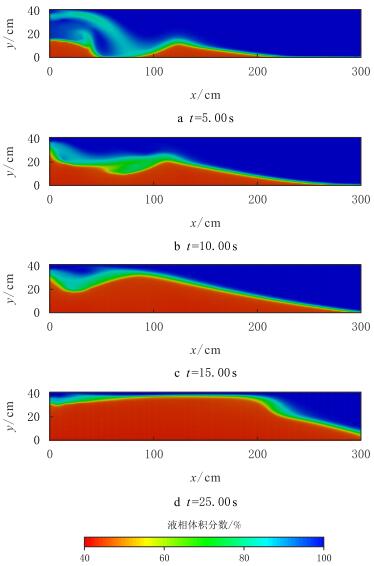 |
| 图7 进口位于顶部时液相体积分布 Fig. 7 Liquid volume fraction at bottom inlet boundary |
图 8为支撑剂密度为2~500~kg/m$^3$条件下的液相分布。对比图 9(撑剂密度2~000~kg/m$^3$)看,支撑剂密度减小后,砂丘中心位置向后移动(图 8中砂丘中心距进口约95~cm),进口附近很少有支撑剂颗粒堆积。颗粒流化能力增强,即图 8a中砂丘顶部红色向蓝色过渡区域变宽。图 8b中砂丘高度不断增加,图 8c中砂丘高度也接近平衡高度。图 8d支撑剂床的扩展过程与图 2d基本相同,但平衡高度稍大。
在图 9中,支撑剂颗粒密度减小后,砂丘中心位于距进口约100~cm处(图 9a),进口附近支撑剂被全被带走。可见颗粒流化能力进一步加强,支撑剂在砂丘背后很快被输运到出口端。由于支撑剂的流出,图 9c中砂丘没有达到平衡高度。支撑剂床的扩展过程仍然与密度较大的情况相同,但平衡高度进一步增大(图 9d)。
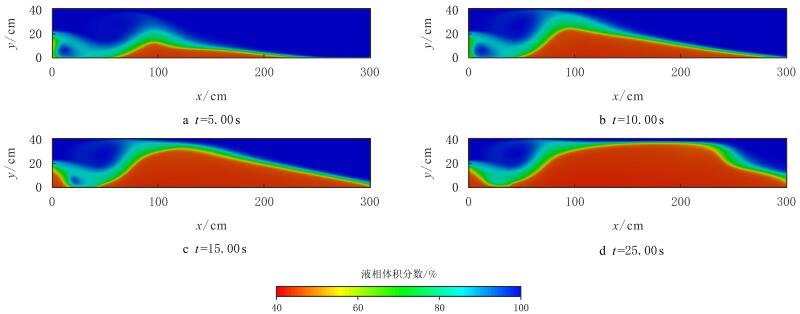 |
| 图8 支撑剂密度为2~500~kg/m$^3$时液相分布 Fig. 8 Liquid volume fraction at density of 2~500~kg/m$^3$ |
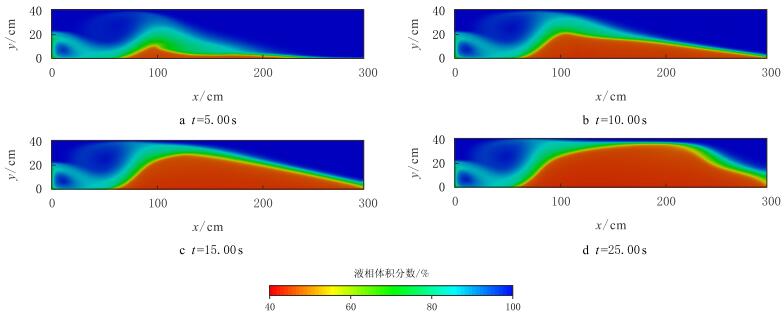 |
| 图9 支撑剂密度为2~000~kg/m$^3$时液相分布 Fig. 9 Liquid volume fraction at density of 2~000~kg/m$^3$ |
(1) 对比数值模拟与实验研究表明:两流体两相流模型能够准确捕捉支撑剂颗粒在清水压裂液中的输运沉降行为,表明该模型能够适应这种支撑剂输送的裂缝内两相流动。
(2) 进口的位置对支撑剂的铺设影响重大,不适当的进口位置会造成近井附近形成无支撑区域,降低压裂效果。
(3) 射流速度增大、支撑剂密度减小都能提升支撑剂输运能力、增大沉降距离,同时增大颗粒被流化的能力(平衡高度增大)。
(4) 射流进入裂缝后的流动结构(回流、旋涡等)近井附近的支撑剂的铺设有重要影响。
| [1] |
温庆志, 翟恒立, 罗明良, 等. 页岩气藏压裂支撑剂沉降及运移规律实验研究[J].
油气地质与采收率, 2012, 19 (6) : 104–107.
Wen Qingzhi, Zhai Hengli, Luo Mingliang, et al. Study on proppant settlement and transport rule in shale gas fracturing[J]. Petroleum Geology and Recovery Efficiency, 2012, 19 (6) : 104–107. |
| [2] | Britt L,Smith M,Haddad Z,et al. Waterfracs:We do need proppant after all[C]. SPE 102227, 2006. |
| [3] | Palisch T, Vincent M, Handren P. Slickwater fracturing:Food for thought[J]. SPE Production & Operations, 2010, 25 (3) : 327–344. |
| [4] | Gadde P B, Sharma M M. The impact of proppant retardation on propped fracture length[C]. SPE 97106, 2005. |
| [5] | Wang J, Joseph D D, Patankar N A, et al. Bi-power law correlations for sediment transport in pressure driven channel flows[J]. International Journal of Multiphase Flow, 2003, 29 (3) : 475–494. DOI:10.1016/S0301-9322(02)00152-0 |
| [6] | Eskin D. Modeling non-Newtonian slurry convection in a vertical fracture[J]. Chemical Engineering Science, 2009, 64 (7) : 1591–1599. DOI:10.1016/j.ces.2008.12.019 |
| [7] | Tsai K, Fonseca E, Degaleesan S. Advanced computational modeling of proppant settling in water fractures for shale gas production[C]. SPE 151607, 2012. |
| [8] | Agrawal K, Loezos P N, Syamlal M, et al. The role of meso-scale structures in rapid gas-solid flows[J]. Journal of Fluid Mechanics, 2001, 445 (1) : 151–185. |
| [9] | Wang W, Li J. Simulation of gas-solid two-phase flow by a multi-scale CFD approach of the EMMS model to the sub-grid level[J]. Chemical Engineering Science, 2007, 62 (1) : 208–231. |
| [10] | Srivastava A, Sundaresan S. Analysis of a frictionalkinetic model for gas-particle flow[J]. Powder Technology, 2003, 129 (1) : 72–85. |
| [11] | Benyahia S, Syamlal M, O'Brien T J. Evaluation of boundary conditions used to model dilute, turbulent gas/solids flows in a pipe[J]. Powder Technology, 2005, 156 (2) : 62–72. |
| [12] | Kaushal D R, Thinglas T, Tomita Y, et al. CFD modeling for pipeline flow of fine particles at high concentration[J]. International Journal of Multiphase Flow, 2012, 43 : 85–100. DOI:10.1016/j.ijmultiphaseflow.2012.03.005 |
| [13] | Benyahia S. On the effect of subgrid drag closures[J]. Industrial & Engineering Chemistry Research, 2009, 49 (11) : 5122–5131. |
| [14] | Syamlal M, Rogers W, O'Brien T J. MFIX documentation:Theory guide[R]. DOE/METC-94/1004, National Technical Information Service, 1993. |
| [15] | Liu Yajun. Settling and hydrodynamic retardation of proppants in hydraulic fractures[D]. Texas:The University of Texas, 2006. |
 2014, Vol. 36
2014, Vol. 36

