随着计算机技术的发展,储层地质模型已经成为油田地质研究成果的综合反映。油气藏静、动态特征认识的局限性导致了对地下地质体表征结果存在不确定性,因此,这种对地下油气储层认识的不确定性将必然体现在储层地质模型中,影响地质模型的准确性。
以往,利用随机地质建模技术,通过多次随机实现生成多个地质模型,并基于有限的地质模型开展敏感性与不确定性分析[1-4]。目前,地质建模技术趋势大体表现为:储层地质模型的网格精度越来越高,一般都有上百万个网格,有时多则可达几千万个网格;建模流程越来越复杂,例如将确定建模与随机建模相结合[5],相控建模过程进一步细化,实现多步相控建模;约束数据体的使用越来越多[6],在相模型与岩石属性模型中使用不同的约束数据体,甚至在同一属性建模过程中,也考虑使用多种(地震)属性体融合约束;另外,敏感性参数的考虑也越来越全面,目前不确定性参数也延展到几乎所有的建模过程中。
正是由于上述原因,地质建模的时间越来越长、地质模型数据越来越多、建模过程中对计算机内存与硬盘要求越来越高。导致理论上可以实现的敏感性分析与不确定性研究,在实际操作过程中举步维艰。基于上述情况,在储层地质建模过程中,引入响应面代理模型,能较好地适应基于储层地质模型的不确定性分析,快速高效。
2 响应面代理模型响应面代理模型是相对简单的模型,它是基于响应值与训练样本(数据)之间的最小二乘法拟合结果。这个代理模型适用于表征真实模型的全局趋势,而忽略局部振荡误差。
建立响应面代理模型,就是在满足一定精度条件下,求解可以替代真实模型的响应模型(或称函数),进而为快速研究不确定性、敏感性分析及方案优化服务[6-14]。常用的代理模型建模方法有多项式响应面法、Kriging法、径向基函数法、神经网络法等[14]。在各种地质建模与开发方案优化过程中,考虑到拟合的精度和效率,普遍采用二次多项式响应面模型[10-11],其数学表达式如下
| $ \hspace{-1em}f\left( x \right) = {\beta _0} + \mathop \sum \limits_i {\beta _i}{x_i} + \mathop \sum \limits_i \mathop \sum \limits_j {\beta _{ij}}{x_i}{x_j} + \mathop \sum \limits_i {\beta _{ii}}x_i^2 + \varepsilon $ | (1) |
式中:$f(x)$——待求值(或预测变量);$x_i$,$x_j$——自变量;$\beta_0$,$\beta_i$,$\beta_{ij}$,$\beta_{ii}$——对应于各自变量的系数;$\varepsilon$——随机误差,即代理模型中的响应值与真实模型值之间的误差。
$\beta$为建立二次响应面模型的关键。根据训练样本进行建立代理模型时,基于最小二乘法可求得$\beta$系数,以满足代理模型与实际模型之间的响应偏差最小化。若误差平方和远大于0,也意味着样本数据允许响应面方程作进一步的微调,那么就可能需进行所谓的代理模型正则化,以突出关键参数(自变量)。
3 基于响应面代理模型的不确定性研究流程与关键点 3.1 主要研究步骤地质模型的不确定性分析及最后的地质模型筛选,是储层地质建模的关键与建模成果的最终体现。基于响应面代理模型的不确定性研究流程如图 1所示,主要包括4个步骤。
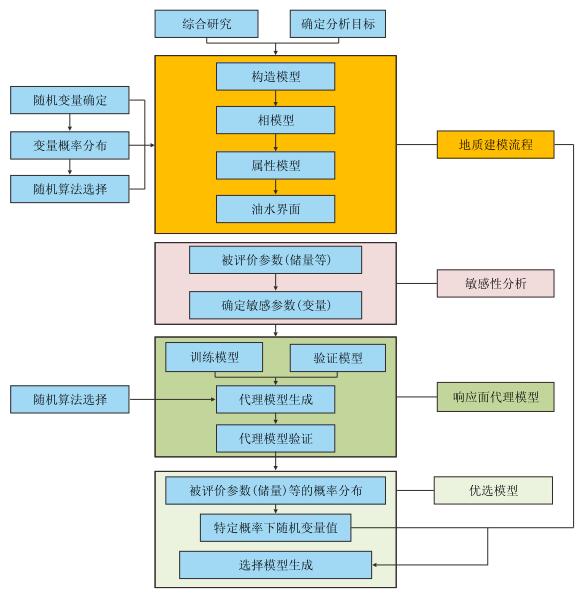 |
| 图1 基于响应面代理模型的不确定性研究流程 Fig. 1 Workflow for the uncertainty study based on the response-surface proxy model |
根据油气田储层发育特点,考虑资料丰富程度,建立能充分反映最终地质模型(或地质储量、开发生产指标等)的流程,并能满足最终待评价定量参数(如地质储量、可驱替储量等)的不确定性分析及与其相关因素(如油气界面、储层下限值等)的模拟要求。
(2) 敏感性参数设计与关键敏感性参数的筛选根据综合地质研究成果,分析影响储层地质模型生成的各种参数,并统计分析各参数概率分布,拟合各参数概率分布模型。利用敏感性分析技术,筛选出关键敏感性参数,并作为代理模型的输入参数。
(3) 建立基于响应面的代理模型首先,根据第(1)步的地质模型流程,随机生成一定数量的地质模型,分别作为生成代理模型所需的训练模型及用于检验代理模型适用性的验证模型;其次,将之前筛选出的关键敏感性参数作为自变量,以训练模型为基础,形成多项式响应面代理模型;最后,利用生成的验证模型对代理模型进行验证,以检验响应面代理模型的适用性。
(4) 不确定性分析与模型优选使用Monte-Carlo法,依据关键敏感性参数的概率分布模型,随机采样,生成自变量数据对,应用响应面代理模型,生成相应的响应值。利用这些基于代理模型形成的值就可以开展诸如地质储量等定量参数的不确定性分析,确定各概率值下对应的待评价参数(如地质储量),进而筛选出对应值下的地质模型。
3.2 关键点在上述流程处理过程中,存在以下影响建模结果及不确定性分析的关键点。
(1) 建模流程首先,构造、沉积相及储层属性等各个建模过程须能表征各建模环节(如构造误差、砂体边界、储层属性等)的不确定性;其次,影响最终待评价定量参数(如地质储量、开发生产指标等)的其他控制因素(如油气界面、储层下限值等)等的随机模拟过程也需符合地质规律。
(2) 敏感性参数因精细地质模型的网格数太多,建模过程复杂、耗时长且对计算机硬件要求高,若考虑每一个敏感性参数,一方面影响了随机模拟的时间效率,另一方面也影响到代理模型的建立。因此,如何从多个敏感性参数中,选择关键敏感性参数至关重 要。
(3) 随机变量的采样方式响应面代理模型建立之前,必须生成相当数量的随机模型分别作为训练模型与验证模型,在这一过程中,涉及随机变量的采样方式。目前较普遍的采样方式包括Box-Behnken、Latin-Hypercube,Monte-Carlo等[7]。实际上,在基于随机地质建模不确定性分析中,常通过实验设计来实现变量的采样与训练样本的生成[1, 3, 12-15]。严格意义上来讲,代理模型应该既能反映高概率的真实模型,也能代表低概率下的真实模型。因此,在有限的模拟次数下,应尽可能保证所生成的地质模型覆盖待评价定量参数(预测变量,如地质储量)的低、中、高值,故基于等累计概率区间的采样方式(如Box-Behnken、Latin-Hypercube等)优于依概率发生高低的采样方式(Monte-Carlo),这也就是地质建模中样本的实验设计合理性所在。但须注意的是,若代理模型不能很好地拟合待评价参数或自变量概率分布函数并不均衡时,应考虑概率高低区间的拟合,这种情况下,应用实验设计形成的响应面代理模型不一定能真实地反映预测变量[15-16]。
当代理模型确定下来后,可利用响应面代理模型进行不确定性分析。代理模型计算速度快,可使用足够多的输入变量数据对,短时间内完成大批量的运算,缘于此,使用Monte-Carlo法实现大批量的采样,从而相对真实地获取待评价参数(如地质储量)的概率分布。
(4) 模型优选它是不确定性研究结果的直接应用。在应用响应面代理模型时,须记录下各自变量数据对及相应的代理模型响应值,通过对应于某一概率值的代理模型响应值就可以得到自变量数据对。通过设定自变量数据对,运行建模流程,即可生成某概率值对应的地质模型。例如,分析地质储量的不确定性时,得到了其对应的$P_{90}$、$P_{50}$与$P_{10}$值(或更多其他概率),后续的开发方案优化将基于这3个概率地质储量值所对应的地质模型,进而可得到基于不同概率储量的开发指标及经济评价结果。
4 应用实例A油田位于尼日利亚海上深水区,主力产层为深水斜坡重力流沉积的复合水道砂体,水道砂体呈现纵向叠置、水平方向迁移的发育特点。该油田主力油藏L细分为L$_1$、L$_2$及L$_3$3个小层。L油藏注水开发,以水平生产井为主,目前共有10口井钻遇L油藏。
4.1 建模流程的敏感参数及敏感性分析该油田研究中的不确定性包括了构造深度变化、储层分布、油水界面、有效储层孔隙度下限值等多个方面,将这些敏感参数设为具概率分布的随机变量,在建模流程运行时同时变化,且在概率分布的各区间内随机取值。
4.1.1 建模流程中敏感性参数 (1) 构造模拟储层地质建模过程中,通常不考虑构造的不确定性。实际上,无论是评价井还是后续所钻的生产井,钻前预测深度和钻后实际深度均存在深度误差。海上油气田大多为成批设计、成批钻井,构造误差更是不可避免。构造深度的预测误差是影响油气储量的关键因素之一。钻遇L油藏各井(包括评价井与生产井)钻前/后误差分析结果如图 2所示,深度误差变化范围为{\twodash}49~+23 m,偏差为10 m。
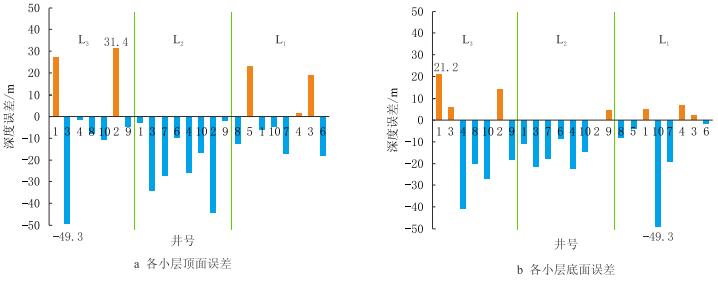 |
| 图2 钻遇L油藏各井钻前预测与钻后实际构造深度对照 Fig. 2 Depth differences between the prognoses and the actual results in wells penetrated into L reservoir |
通过两种方法实现构造深度不确定模拟:① 以解释的构造深度网格作为基础面,针对每一顶面网格单元,将构造偏差作为随机变量,井点分层为约束数据,平均生产井距作约束半径,随机生成对应于每次地质模型实现的构造面;② 分析构造深度误差的概率分布,形成概率分布模型,应用Monte-Carlo法随机生成每个顶面网格构造误差数据,同样也以井点分层为约束数据,平均生产井距作约束半径,随机生成对应于每次地质模型实现的构造面(图 3)。在已有井点控制区域,构造面变化不大,但在无钻井控制区域,构造面存在较大的不确定性,反映了油田的实际钻探结果。
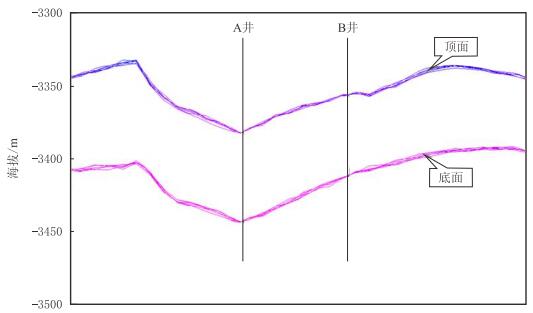 |
| 图3 建模流程中考虑构造误差的多次随机实现(不同线代表不同的实现) Fig. 3 Multiple stochastic-simulation realizations for two horizons considering the structural errors in the process of geo-modeling(Lines in different color represents different realizations) |
本区储层为深水重力流水道沉积复合砂体,通过井震结合,对复合砂体构型单元进行了解释,得到复合砂体框架。储层模拟分为相模拟及储层属性模拟。相模拟分为两个过程,首先,根据井震信息确定复合砂体外部构型,接着在复合砂体外部构型约束下,根据测井与岩芯确定的井点微相,应用序贯指示模型(SIS)生成微相模型;然后,在相控原则下,根据井点与地震平面属性,应用协克里金模拟,生成物性参数(如孔隙度)模型。研究区影响储层模拟因素为属性模拟时各方向的变差函数参数变程。在此利用地震平面属性扫描确定平面主变程方向及主、次变程范围(表 1,图 4),在建模流程中将各主、次变程设为随机变量。
| 表1 L油藏各小层孔隙度模拟时主次变程范围 Table 1 The ranges in the major and minor directions for all sub-units in L reservoir |
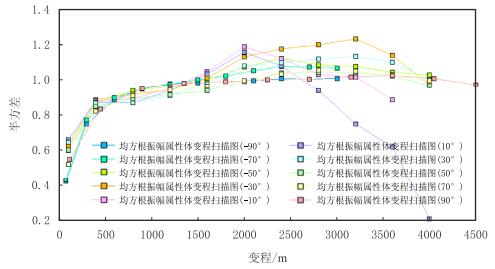 |
| 图4 L油藏随机模拟时的实验变差函数扫描与主次变程范围确定 Fig. 4 Scanning of the experience variograms and determining of the ranges in the major and minor directions for one unit in L reservoir |
由于钻遇L油藏的所有井均未钻遇油水界面,早期储量研究时,根据本油藏油底、邻近测井解释水顶及根据其下伏水层的压力资料与该油藏油层压力资料确定相应的视油水界面(图 5),尽管三者间的差异较小,但对真实油水界面的认识仍然存在一定的不确定性。为了反映油水界面不确定性与构造深度的不确定性对油气储量的影响,在建模流程中,将油水界面作为随机变量,模拟过程中随机取值,变化范围为油底至压力资料评估值。
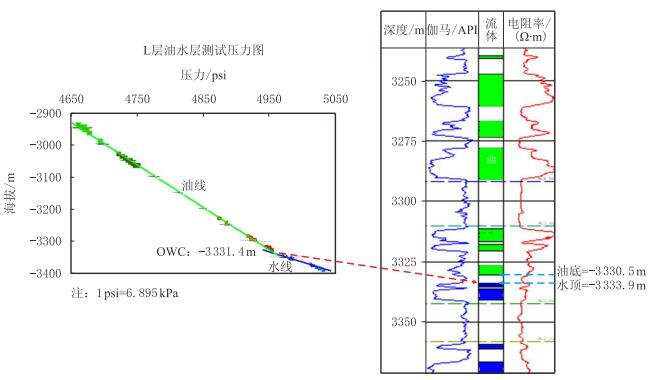 |
| 图5 L油藏随机模拟时的油水界面确定 Fig. 5 Varying ranges for the oil-water contact in the simulation |
就基于地质模型的储量评估而言,区分储层与非储层是本次研究的关键。利用测井与岩芯分析的资料(图 6a)及储量累积丢失曲线(图 6b),可知储层孔隙度下限值为0.10~0.15。故在孔隙度建模流程中,将孔隙度下限值设为敏感性参数,在每次随机模拟中发生服从一定概率分布的随机变化,并使之为有效储层判别标准之一,作用于同次模拟所生成的地质模型,得到该次运行地质模型的有效储层分布。
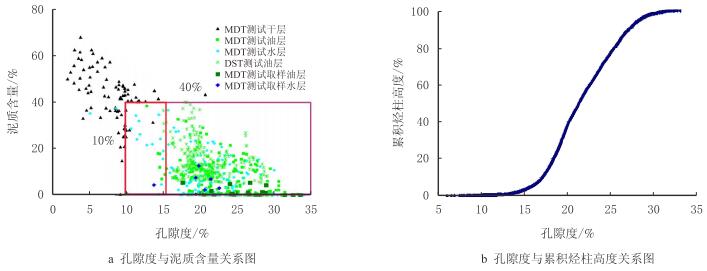 |
| 图6 L油藏储层孔隙度下限值变化范围确定 Fig. 6 Determination for the ranges of the porosity cutoff regarding L reservoirs |
当建模过程中敏感参数设定后,需要了解哪些参数可能对地质储量结果影响大,这将有助于确定响应面代理模型建立时选定哪些参数,即各个参数之间相互比较,确定变量自身的变化对地质储量影响的相对大小。这样在代理模型建立时,可以只考虑那些相对敏感的参数,而不考虑那些不敏感的参数,从而更好地保证代理模型的收敛性。
基于地质建模的敏感性分析,运行已建好的建模流程(图 1),将需分析的变量设定为随机变量,而其他参数设定为其概率为$P_{50}$所对应的值。本研究过程中对每一参数的敏感性分析分别运行100次,获取各随机地质模型所对应的地质储量。各变量敏感性所对应的随机地质模型地质储量分布(图 7)表明,研究区构造变化与储层分布(变差函数变程大小)对地质储量影响相对较大。考虑到本区敏感性参数相对较少,因此这些敏感性参数都被反映到代理模型中。
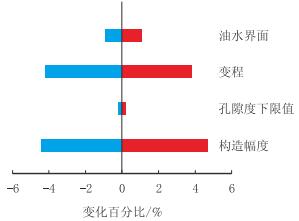 |
| 图7 各随机变量与地质储量的敏感性分析 Fig. 7 Sensitivities of all variable parameters with regard to the original oil in place |
由于随机地质建模对计算机内存与硬盘要求较高,且运算时间长,基于建模流程进行地质储量分布预测时不易达到真实结果,因此,在储层地质建模过程中引入响应面(Response surface)生成的代理模型。
本次研究中考虑了建模过程中的所有敏感参数(构造深度误差、物性参数模拟的变差函数变程、油水界面及孔隙度参数),应用Latin-Hypercube取样方法,生成40个地质模型,分别作为生成响应面代理模型的训练模型及验证模型。比较代理模型计算的地质储量值与由验证模型计算的地质储量值(图 8),两者之间的误差小,说明本研究的代理模型可以代表基于建模生成的地质模型,可以用于地质储量的不确定性研究。
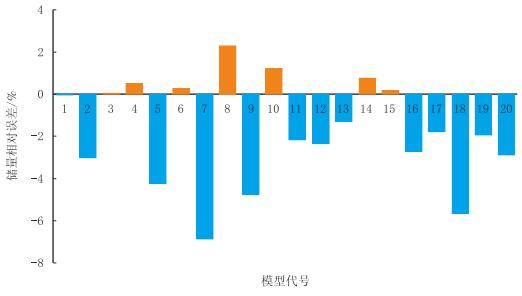 |
| 图8 基于响应面的代理模型与验证模型所计算地质储量相对误差 Fig. 8 Relative errors of the original oil in place derived respectively from the response-surface proxy and the validation geomodels |
本次研究是围绕地质储量这一定量参数进行的不确定性分析,并基于此进行模型筛选。考虑到代理模型可以快速实现大量计算,在取样算法上应用Monte-Carlo法,生成了5 000对敏感性参数(并存取),应用已形成的响应面代理模型计算地质储量,得到各概率下的地质储量(图 9)。
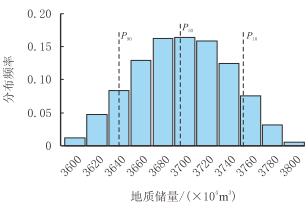 |
| 图9 基于响应面代理模型所计算的地质储量概率分布 Fig. 9 Probability distribution of the original oil in place for L reservoir estimated from the response-surface proxy |
基于地质储量的概率值(如$P_{10}$、$P_{50}$、$P_{90}$),可以筛选出相应的敏感参数对。通过这些敏感参数对,运行图 1中的建模流程就可以得到相应的地质模型。这些优选出的地质模型可以服务于后续的基于不同地质储量的开发方案及经济评价等方面的研究。
本次研究中从训练模型与验证模型的生成到代理模型形成所用时间大约在4 h,基于代理模型所进行的地质储量概率分析不到1 min,整个时间约4 h即可完成。如果使用常规不确定性分析,当存取地质模型的情况下,除了对内存要求极高之外,从运行时间上来看,一般的计算机也几乎难以完成。
5 结 论(1)综合地质研究成果的定量体现是数学地质模型,基于地质模型的定量研究及不确定性分析是目前油藏描述趋势。受计算机硬件限制,很难做到真正、完全基于随机地质模型的不确定性分析,因此,快捷、近似的算法将有利于随机地质建模技术的应用。
(2)运用随机地质建模技术进行地质参数的不确定性分析时,应从储层地质特征分析入手,筛选敏感性参数,确定其变化范围及概率分布模型(在数据样本点足够情况下,应进行参数的概率分布模型研究)。
(3)在一定条件下,响应面代理模型可以满足基于地质模型的不确定性分析,可以得到待评价参数(如地质储量)相对客观、真实的概率分布,并获得各概率下的地质模型,进而为油藏数值模拟及经济评价服务,为方案优化服务。
(4)基于响应面代理模型的不确定性研究思路可以一体化地应用于油田开发方案编制全过程,即储层地质建模$\rightarrow$油藏数值模拟$\rightarrow$工程经济评价。
| [1] |
霍春亮, 刘松, 古莉, 等. 一种定量评价储集层地质模型不确定性的方法[J].
石油勘探与开发, 2007, 34 (5) : 574–579.
Huo Chunliang, Liu Song, Gu Li, et al. A quantitative method for appraising reservoir geological model uncertainty[J]. Petroleum Exploration and Development, 2007, 34 (5) : 574–579. |
| [2] |
孙立春, 高博禹, 李敬功. 储层地质建模参数不确定性研究方法探讨[J].
中国海上油气, 2009, 21 (1) : 35–38.
Sun Lichun, Gao Boyu, Li Jinggong. A discussion on the method to study uncertainty of geologic modeling parameters[J]. China Offshore Oil and Gas, 2009, 21 (1) : 35–38. |
| [3] |
薛艳霞, 廖新武, 赵春明, 等. 基于随机建模技术的油田开发初期河流相储层不确定性分析方法——以渤海A油田为例[J].
岩性油气藏, 2012, 24 (1) : 80–83.
Xue Yanxia, Liao Xinwu, Zhao Chunming, et al. Uncertainty analysis of fluvial reservoir in oilfield early development period based on stochastic modeling:A case study from A Oilfield in Bohai Bay[J]. Lithologic Reservoirs, 2012, 24 (1) : 80–83. |
| [4] |
王根久, 赵丽敏, 李薇, 等. 随机建模中变差函数的敏感性研究[J].
石油勘探与开发, 2005, 32 (1) : 72–75.
Wang Genjiu, Zhao Limin, Li Wei, et al. Sensitivity of variogram in stoehastic modeling[J]. Petroleum Exploration and Development, 2005, 32 (1) : 72–75. |
| [5] |
吕晓光, 张永庆, 陈兵, 等. 深度开发油田确定性与随机建模结合的相控建模[J].
石油学报, 2004, 25 (5) : 60–64.
Lü Xiaoguang, Zhang Yongqing, Chen Bing, et al. Facies controlled modeling for mature developed oilfield by integrating determinacy and stochastic methods[J]. Acta Petroei Sinica, 2004, 25 (5) : 60–64. |
| [6] |
吴胜和, 刘英, 范峥, 等. 应用地质和地震信息进行三维沉积微相随机建模[J].
古地理学报, 2003, 5 (4) : 439–449.
Wu Shenghe, Liu Ying, Fan Zheng, et al. 3D stochastic modeling of sedimentary mic-rofacies with geological and seismic data[J]. Journal of Palaeogeography, 2003, 5 (4) : 439–449. |
| [7] |
李俊键, 马佳, 刘勇, 等. 基于代理模型与遗传算法的海上油田聚合物驱注入参数优化控制方法[J].
中国海上油气, 2009, 24 (4) : 41–44.
Li Junjian, Ma Jia, Liu Yong, et al. Optimiziing injection parameters of polymer flooding in offshore oilfields by combining surrogate model and genetia algorithm[J]. China Offshore Oil and Gas, 2009, 24 (4) : 41–44. |
| [8] |
郑玲丽, 李闽, 钟水清, 等. 变围压循环下低渗透致密砂岩有效应力方程研究[J].
石油学报, 2009, 30 (4) : 588–592.
Zheng Lingli, Li Min, Zhong Shuiqing, et al. Research on calculation of effective stress in low-permeability sandstone rock under cyclic loading and unloading[J]. Acta Petroei Sinica, 2009, 30 (4) : 588–592. |
| [9] | 刘大伟, 刘艳艳. 基于代理模型对油藏描述中静动态数据进行优化[J]. 国外油田工程, 2007, 23 (6) : 17–20. |
| [10] |
李典庆, 周创兵, 陈益峰, 等. 边坡可靠度分析的随机响应面法及程序实现[J].
岩石力学与工程学报, 2010, 29 (8) : 1514–1523.
Li Dianqing, Zhou Chuangbing, Chen Yifeng, et al. Reliability analysis of slope using stochastic Response surface method and code implementation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29 (8) : 1514–1523. |
| [11] |
王峰, 向祖平, 陈中华, 等. 利用响应曲面法校正气藏储层应力敏感性曲线[J].
西南石油大学学报:自然科学版, 2010, 32 (5) : 96–99.
Wang Feng, Xiang Zuping, Chen Zhonghua, et al. Correct reservoir stress sensitivity curve by using response surface method[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32 (5) : 96–99. |
| [12] | Artun E, Ertekin T, Watsonet R, et al. Development of universal proxy models for screening and optimization of cyclic pressure pulsing in naturally fractured reservoirs[J]. Journal of Natural Gas Science and Engineering, 2011, 3 : 667–686. DOI:10.1016/j.jngse.2011.07.016 |
| [13] | Akshay Sahni. Case studies of uncertainty analysis in the seismic to reservoir simulation workflow[C]. SPE 84188, 2003. |
| [14] | Friedmann F, Chawath'e A, Larue D K. Assessing uncertainty in channelized reservoirs using experimental designs[C]. SPE 71622, 2001. |
| [15] | Li Heng, Sarma P, Zhang Dongxiao. A comparative study of the probabilistic-collocation and experimental-design methods for petroleum-reservoir uncertainty quantification[J]. SPE Journal, 2011, 16 (2) : 429–439. DOI:10.2118/140738-PA |
| [16] | Lawal K A. Modeling subsurface uncertainties with experimental design:Some arguments of non-comformist[C]. SPE 128350, 2009. |
 2014, Vol. 36
2014, Vol. 36

