2. 中国石化华东石油工程有限公司固井分公司, 江苏 扬州 225101
2. Cementing Engineering Company, Huadong Petroleum Administration, SINOPEC, Yangzhou, Jiangsu 225101, China
气体钻井以其不可比拟的优越性越来越受到人们的青睐[1],以气体作为循环介质,是最常用的欠平衡钻井技术之一,排砂管线是气体钻井不可缺少的地面设备之一,通常在实际工程中忽略了其安全性。常规的气体钻井设计[2-8]主要考虑注气量、井壁稳定性问题、井下燃爆、钻压转速等钻井参数,而忽视了地面排砂管线流场、受力以及其冲蚀损坏机理方面的研究。一旦排砂管线发生冲蚀破坏,将对现场工作人员和井场的环境造成重大的安全事故,为此本文对气体钻井排砂管线进行系统的现场调研和安全性评价,针对现场实际情况,重点研究排砂管线突变的弯接头处冲蚀损害机理,为改进和优化弯接头提供理论依据,以提高气体钻井地面的安全性为目的。
气体钻井返排出井口的气体中含有大量的岩屑颗粒,这些颗粒在高速气流的作用下,对排砂管线的过渡区域将产生严重的冲蚀和侵蚀磨损,使其壁厚变薄,最终使排砂管线发生刺穿或断裂,导致其混合的天然气爆炸和燃烧[9-10]。因此排砂管线的冲蚀机理涉及到计算流体动力学(CFD)和其强度破坏的固体力学的研究,本文将对气体钻井排砂管线过渡区域的弯接头进行理论研究、CFD流场模拟研究和强度研究。
1 物理模型 1.1 控制方程在气体钻井中,从井底环空高压返排出的气体在井口低压下,发生气体膨胀而产生高速气流,此高速气流在排砂管线内将产生严重的紊流,因此其流动控制方程必须用流体紊流控制方程。根据流体动力学理论,RNG k-ε紊流模型对具有分离和二次流的紊流流动具有较好的模拟性,既适应高雷诺数的紊流流动也适应于低雷诺数的紊流流动,模型常数是利用RNG方法精确推导出来的[11-13],适合本文所研究的排砂管线弯头冲蚀机理研究模型。
| $ \dfrac{\partial }{{\partial t}}\left( {\rho k} \right) + \dfrac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \dfrac{\partial }{{\partial {x_j}}}\left( {{\alpha _{\rm{k}}}{\mu _{{\rm{eff}}}}\dfrac{\partial }{{\partial {x_j}}}} \right) +\\ \hspace{2em} {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} + {S_{\rm k}} $ | (1) |
| $ \dfrac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \dfrac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \dfrac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\dfrac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) +\\ {{\rm C}_{1\varepsilon }}\dfrac{\varepsilon }{k}\left( {{G_{\rm k}} + {{\rm C}_{3\varepsilon }}{G_{\rm{b}}}} \right) - {{\rm C}_{2\varepsilon }}\rho \dfrac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon } $ | (2) |
式中:
t-时间,s;
ρ-连续相密度,kg/m3;
k-湍动能,J;
$x_i$,$x_j$-位移,m,下标i,j=1,2,3,代表x、y、z坐标轴,i$\neq$j;
$u_i$-速度,m/s;
$\alpha_{\rm k}$-k方程的湍流Prandtl数,J;
$\alpha_\varepsilon$-ε方程的湍流Prandtl数,J;
$\mu_{\rm {eff}}$-有效黏度,Pa$\cdot$s;
$G_{\rm {k}}$-由层流速度梯度而产生的湍流动能,J;
$G_{\rm {b}}$-由浮力而产生的湍流动能,J;
ε-湍流耗散率,J/s;
$Y_{\rm {M}}$-由于在可压缩湍流中过渡的扩散产生的波动贡献值,J;
$S_{\rm k}$,$S_\varepsilon$-自定义参数,无因次;
C$_{1 \varepsilon}$,C$_{2 \varepsilon}$,C$_{3 \varepsilon}$-经验常数,无因次;
$R_{\rm {\varepsilon}}$-ε的函数。
1.2 冲蚀磨损模型Finnie的侵蚀磨损理论[14]
| $ \begin{array}{l} v = \dfrac{M v_{\rm p}^2}{{{\sigma _{\rm y}}\psi l}}{\rm{sin}}2\alpha - \dfrac{6}{l}{\rm{sin}}^2\alpha (\alpha < \alpha_0)\\ v = \dfrac{{M{v_{\rm p}^2}}}{{{\sigma _{\rm y}}\psi l}}{\rm{\cdot}}\dfrac{6}{l}{\rm{co}}{{\rm{s}}^2}\alpha (\alpha\geqslant\alpha_0) \end{array} $ | (3) |
式中:
v-材料的体积损耗速度,m3/s;
M-砂粒的总质量,kg;
$v_{\rm p}$-砂粒速度,m/s;
α-冲蚀攻角,rad;
$\sigma_{\rm y}$-材料的屈服应力,Pa;
$\psi$-砂粒的切削深度与砂粒和表面的接触高度之比,无因次;
$\alpha_0$-${\alpha _0}={\rm{arctan}}\dfrac{k}{6}$;
l-砂粒所承受的垂直分量与水平分量之比,无因次。
将式(3)模型应用于排砂管线在气体钻井时的砂粒冲蚀磨损机理研究。固体颗粒在管线壁面上的冲蚀,可通过式(4)计算得到N个岩屑颗粒在气体携带下冲蚀排砂管线的冲蚀速率[13-19],在现场排砂管线所选用的材料均为碳钢,固体颗粒对于碳钢的冲蚀速率可用式(5)计算[14]
| $ E_{\rm R}= \sum\limits_{n = 1}^N \dfrac{{m_{{\rm p}n}}C(d_{{\rm p}n})f(\alpha)v{'_{{\rm{p}}n}}^{b(v{'_{{\rm{p}}n}})}}{A_{\rm f}} $ | (4) |
| $ E_{\rm {Ri}} = 1.559{{\rm{e}}^{ - 6}}{B^{ - 0.59}}{f_{\rm{s}}}{\bar{v_{\rm p}}^{1.73}}f(\alpha ) $ | (5) |
| $ v{'_{{\rm{p}}n}}^{b(v{'_{{\rm{p}}n}})} = v{'_{{\rm{p}}n}}^{1.73} $ | (6) |
| $ C({d_{\rm{p}}}) = 1.559{{\rm{e}}^{ - 6}}{B^{ - 0.59}}{f_{\rm{s}}} $ | (7) |
式中:
$E_{\rm R}$-冲蚀速率,kg/(m3$\cdot$s);
$m_{\rm p}$-砂粒的质量流量,kg/s;
$d_{\rm p}$-砂粒的直径,mm;
$C (d_{\rm p})$-颗粒直径函数;
$f (\alpha)$-冲蚀攻角函数;
N-最大砂粒数,无因次;
$v'_{\rm p}$-砂粒相对速度,m/s;
B-布氏硬度,N/mm2;
$\bar{v_{\rm p}}$-平均砂粒速度,m/s;
$f_{\rm{s}}$-砂粒的形状系数,无因次,$f_{\rm{s}}$=0.20表示砂粒为圆球形,
$f_{\rm{s}}$=0.53表示半圆砂粒,$f_{\rm{s}}$=1.00表示颗粒外形锋利;
$b (v_{\rm p})$-相对速度函数;
$A_{\rm{f}}$-排砂管线单位冲蚀面积,m2;
$E_{\rm {Ri}}$-碳钢冲蚀速率,kg/(m3$\cdot$s)。
由式(7)可知,B越大,材料越坚硬,$C (d_{\rm p})$越小,整体冲蚀速率越小。$f_{\rm{s}}$越小,对管壁的冲蚀越小,$f_{\rm{s}}$越大,对管壁的冲蚀越大,砂粒的形状系数一般在0.50~0.70,根据经验,$f_{\rm{s}}$=0.60符合本文研究的排砂管线冲蚀机理研究的实际情况。
| $ f(\alpha ) = \left\{ \begin{array}{l} - 38.4{\alpha ^2} + 22.7\alpha + 0 (\alpha < 0.267)\\ 3.147{\cos ^2}\alpha \sin \alpha + 0.3609{\sin ^2}\alpha + 2.532 (\alpha\geqslant0.267)\\ \end{array} \right. $ | (8) |
根据式(8)可以得出排砂管线冲蚀攻角与冲蚀攻角函数$f (\alpha)$[20-22]的曲线如图 1所示。
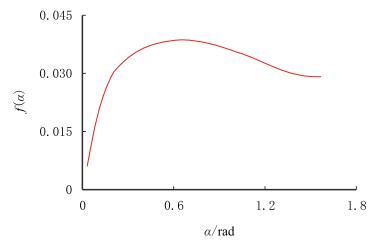 |
| 图1 冲蚀攻角函数 Fig. 1 Angle of attack function |
从图 1可知,冲蚀攻角α很小时,函数值也很小,随着冲蚀攻角的增大,冲蚀攻角函数值逐渐增加,随后逐渐变小。当冲蚀攻角α=0.665时,冲蚀攻角函数为最大值,即在其他条件不变的情况下冲蚀最严重。该冲蚀模型考虑了弯接头的材料、砂粒的形状和密度,能很好地模拟本文气体钻井中弯接头的冲蚀机理研究。
1.3 固体颗粒受力分析在排砂管线中,固体颗粒主要受到本身的重力作用,除此之外,还受到压力梯度、浮力、附加质量力、萨夫曼升力、气-固相互作用力以及与管壁的冲撞力等,是一个复杂的受力环境。这几种力的数学模型见式(9)~式(13)[23]。
| $ W = {V_{\rm{p}}}{\rho _{\rm{p}}}{\rm{g}} $ | (9) |
| $ {F_{\rm{p}}} = - \dfrac{{\pi d_{\rm{p}}^2}}{6}\dfrac{{\partial p}}{{\partial l}} $ | (10) |
| $ {F_{\rm{B}}} = {V_{\rm{p}}}{\rho _{\rm{g}}}{\rm{g}} $ | (11) |
| $ {F_{\rm{m}}} = \dfrac{1}{2}\dfrac{{\pi d_{\rm{p}}^2}}{6}{\rho _{\rm{g}}}{a_{\rm{p}}} $ | (12) |
| $ {F_{{\rm{s}}}} = \dfrac{{5.188{v_{\rm g}^{\frac{1}{2}}}\rho {d_{{\rm{mn}}}}}}{{{\rho _{\rm{p}}}{d_{\rm{p}}}{{\left( {{d_{{\rm{lk}}}}{d_{{\rm{kl}}}}} \right)}^{\frac{1}{4}}}}}(v{\rm{ - }}{v_{\rm{p}}}) $ | (13) |
式中:
W-砂粒受到的重力,N;
$V_{\rm p}$-砂粒的体积,m3;
$\rho_{\rm p}$-砂粒的密度,kg/m3;
g-重力加速度,g=9.8 m/s2;
$F_{\rm p}$-砂粒的压强梯度力,N;
$\dfrac{{\partial p}}{{\partial l}}$-流动方向压强梯度,N/m;\vspace{1mm}
$F_{\rm B}$-浮力,N;
$\rho_{\rm g}$-气体的密度,kg/m3;
$F_{\rm m}$-附加质量力,N;
$a_{\rm p}$-砂粒的加速度,m/s2;
$F_{\rm{s}}$-萨夫曼升力,N;
d-流体变形速率张量,无因次;
下标m,n,k,l-网格节点编号;
$v_{{\rm{g}}}$-气流速度,m/s。
2 排砂管线弯接头CFD模型建立排砂管线过渡区域有圆弧过渡的弯接头和“T”型接头,本文只研究排砂管线弯接头的冲蚀机理,其实体模型见图 2,弯接头内径d=203.2 mm,弯接头半径R=2d=406.4 mm,对弯管角度θ分别为90°,100°,120°,130°,140°,150°,160°,170°进行流场冲蚀分析。根据前面的排砂管线冲蚀机理理论模型和数学模型,以图 2的实体模型为基本结构,建立了对排砂管线弯接头冲蚀机理研究的计算流体动力学(CFD)模型,通过该模型,可以对气体流场任意弯接头的冲蚀破坏研究。
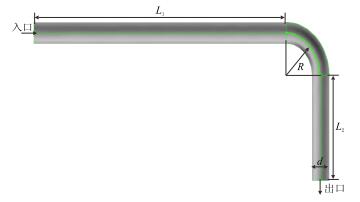 |
| 图2 弯接头实体模型 Fig. 2 Bending joint solid model |
CFD边界条件:整个弯接头模型重力场加速度为9.8 m/s2;入口:气体质量流量分别以Q=1.42 kg/s和Q=0.71 kg/s,即分别为100×104 m3/d和50×104 m3/d气体流量。砂粒的质量流量分别为0.13,0.20,0.26 kg/s,即用215.9 mm钻头分别以约16,23,31 m/h的钻速钻进时砂粒的质量流量,砂粒的粒径为0.26 mm,出口压力为0.1 mPa。
3 冲蚀计算结果和冲蚀机理分析 3.1 冲蚀计算结果分析根据建立的排砂管线弯接头冲蚀机理研究CFD模型,用ANSYS Fluent软件进行仿真模拟计算,得到的结果如图 3~图 6所示。
 |
| 图3 弯接头冲蚀速率云图 Fig. 3 Bending joint erosion rate distribution |
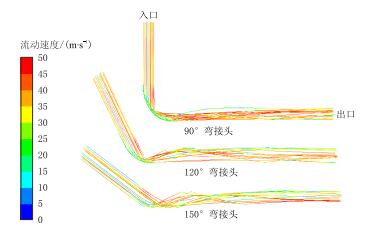 |
| 图4 弯接头砂粒轨迹 Fig. 4 Bending joint sand track |
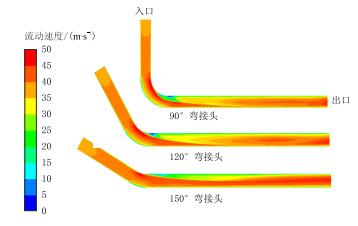 |
| 图5 不同弯接头速度云图 Fig. 5 Velocity distribution of different bending joint |
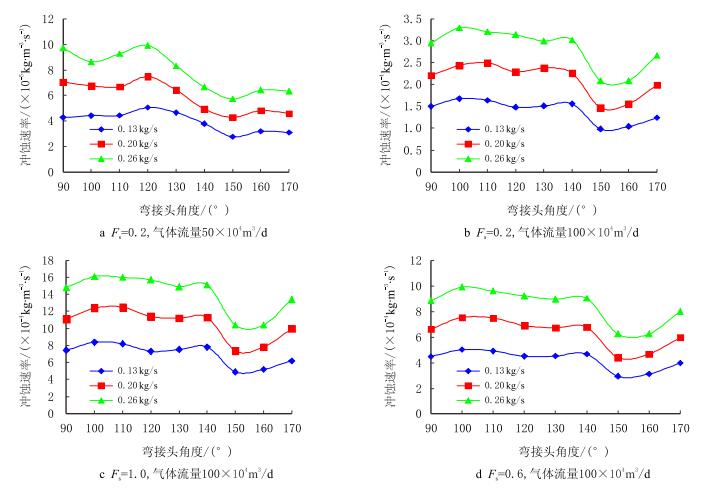 |
| 图6 弯接头冲蚀速率与弯接头角度的关系 Fig. 6 Relationship curves between bending joint erosion rate and bending joint angle |
图 3是90°,120°,150°,170°弯接头在砂粒流量为0.2 kg/s的冲蚀速率云图。砂粒在入口处与气流同速,相当于入口段很长砂粒和气流已达到稳定的流动状态,在气流和砂粒经过入口段到达弯接头处,在重力、压力梯度力、浮力、附加质量力和萨夫曼升力的共同作用下,砂粒对弯接头产生冲击作用。从图 3可知,冲蚀速率最大区域均发生在弯接头区域,并给出了定量的数值,这些冲蚀是由于重力和气流的影响使砂粒撞上管壁并产生冲蚀。受气流的影响,迎流面位于弯接头附近,迎流面冲蚀速率大并存在冲蚀速率最大点,冲蚀速率最大点也就是最容易发生刺漏的点,此处最先发生管壁冲蚀刺穿,附近区域将会被冲蚀得很薄,一旦发生刺穿,刺穿孔将迅速扩大,即弯接头被冲蚀破坏。
图 4是3种不同弯接头处砂粒的流线轨迹图,从图 4中可以更清楚地看到砂粒在管道内的流动和碰撞位置,砂粒在与管壁接触后经反弹和气流、重力的综合作用又与管壁发生碰撞,管道内靠近地面的一侧比远离地面的一侧受到的冲蚀要大,因此,在现场可以通过旋转排沙管线使原先位于靠近地面的一部分朝上,以增大整体管线的使用寿命。
图 5为3种不同弯接头速度云图,从图 5中可以看出,入口段弯头中气流速度很平稳,随着靠近转弯处速度发生变化,弯接头外侧速度小,弯接头内侧速度大。由于流体的惯性,弯头内侧下游部分速度变小,外侧速度变大,随着流体经过弯接头进入直管,流速趋于均匀。整体上流场很流畅,没有发生大的漩涡,只有在弯接头角度较小,流速较大时,气流在惯性的作用下才会发生漩涡,可以得出弯接头角度越大,弯接头对气流的阻力越小,能够优化出最佳的弯接头。
通过对不同砂粒形状系数、不同砂粒流量大量的CFD计算流体动力学仿真模拟,得出了一系列弯接头冲蚀速率与弯接头角度的关系曲线(图 6),由图可知:(1) 砂粒圆球度越高,即形状系数$F_{\rm s}$越小,相同条件下对弯接头的冲蚀越小;(2) 气流量越小,气流和砂粒速度小,砂粒对弯接头的冲蚀越小;(3) 在相同条件下,砂流量越大对弯接头的冲蚀率越高,即冲蚀越严重;(4) 从冲蚀速率与弯接头角度的关系曲线可知,冲蚀速率随弯接头角度的变化而变化,每种工况下都会出现冲蚀速率随弯接头角度变化的最大值和最小值,在研究和设计弯接头结构设计时,应关心冲蚀速率的最小值。从图 6中不同工况下的12条曲线可知,冲蚀速率的最小值发生在150°~160°,即弯接头的最优角度为155°。在气固两相流经过直管时,在重力、压力梯度力、浮力、附加质量力、萨夫曼力共同作用下砂粒的流动方向发生改变,对管道产生冲蚀,但由于冲蚀攻角小,冲蚀速率也较小。
3.2 冲蚀机理分析通过大量的理论研究可知,抵抗冲蚀的能力和自身的材料性能有着密切的关系,目前弯接头所用材料都是碳钢材料。碳钢的布氏硬度越高,$C (d_{\rm p})$越小,对碳钢而言,含碳量越高布氏硬度越高,因此在满足其他条件的情况下管线应选高碳钢。塑性材料在大角度冲蚀(接近90°)时具有良好的耐冲蚀性,但是在小角度冲蚀时的磨损严重。一般而言,最严重的冲蚀发生在15°~20°的冲蚀过程[24]。韧性材料的冲蚀磨损主要是由于颗粒作用下的表面塑性变形、疲劳以及硬颗粒的不断切割。弯头中通过高速气固两相流时,气流所夹带的颗粒对弯头内表面的冲蚀角度小,因此,韧性材料的磨损非常严重。应该增加弯接头的硬脆性,即提高弯接头的布氏硬度,来减小冲蚀。
砂粒经过弯接头时,由于运动方向的改变,砂粒经过数次碰撞,产生对管壁的撞击和磨损是引起弯管磨损的主要原因。砂粒在通过弯管时,大量的砂粒将与管壁表面接触,形成摩擦磨损。通常认为磨损量近似与气流速度的三次方成正比。即:砂粒与管壁接触时的相对速度越大,形成的接触压力越大,产生的接触频率越高,弯管管壁的磨损速度就越快,选用大尺寸管线,在相同气量的情况下,气流速度变小,冲蚀越小。影响弯接头磨损的因素还有砂粒的特性,如粒度、形状、密度、硬度、破碎性及黏性等,以及砂粒的运动状态。砂粒的形状系数越大,在其他条件相同的情况下,冲蚀速率越大。
4 结论(1) 排砂管线弯接头冲蚀破坏主要与气体流速、固相颗粒形状系数、气流冲蚀攻角以及弯接头材料和弯接头角度等有密切的关系,其中,最主要的因素是弯接头的角度和弯接头的材料,其次是气流速度。
(2) 建立的排砂管线弯接头CFD有限元模型,可以任意改变弯接头的角度,定量地模拟不同工况下含有固相颗粒的多相流对弯接头的冲蚀速率和冲蚀机理。
(3) 通过对不同砂粒形状系数、不同砂粒流量的CFD计算流体动力学仿真模拟研究,得出了一系列的弯接头冲蚀速率与弯接头角度的定量关系曲线,冲蚀速率的最小值发生在150°~160°,最终优化弯接头的最优角度为155°。
(4) 排砂管线工作环境恶劣,建议现场经常对排砂管线进行检测和维修,尤其要加强弯接头处壁厚的实时检测,确保排砂管线安全工作和运行。
| [1] |
艾惊涛, 余锐, 廖兵, 等. 四川油气田气体钻井技术现状及发展方向[J].
天然气工业, 2009, 29 (7) : 39–41.
Ai Jingtao, Yu Rui, Liao Bing, et al. The statusquo and future development of gas drilling technology in the Sichuan Gas Field[J]. Natural Gas Industry, 2009, 29 (7) : 39–41. |
| [2] |
李国美, 王跃社, 孙虎, 等. 节流器内液-固两相流固体颗粒冲蚀数值模拟[J].
石油学报, 2009, 30 (1) : 145–148.
Li Guomei, Wang Yueshe, Sun Hu, et al. Numerical simulation on solid particle erosion of solid-liquid two-phase fluid in flow controller[J]. Acta Petrolei Sinica, 2009, 30 (1) : 145–148. |
| [3] |
王治中, 邓金根, 孙福街, 等. 井筒砂粒运移规律室内模拟实验研究[J].
石油学报, 2006, 27 (4) : 130–132,138.
Wang Zhizhong, Deng Jingen, Sun Fujie, et al. Experimental study on sand migration in wellbore[J]. Acta Petrolei Sinica, 2006, 27 (4) : 130–132,138. |
| [4] |
祝效华, 刘少胡, 童华. 气体钻井钻杆冲蚀规律研究[J].
石油学报, 2010, 31 (6) : 1013–1017.
Zhu Xiaohua, Liu Shaohu, Tong Hua. A study on the drill pipe erosion law in gas drilling[J]. Acta Petrolei Sinica, 2010, 31 (6) : 1013–1017. |
| [5] |
郭建华, 余朝毅, 李黔, 等. 气体钻井井筒冲蚀作用定量分析及控制方法[J].
石油学报, 2007, 28 (6) : 129–132.
Guo Jianhua, Yu Chaoyi, Li Qian, et al. Quantitative analysis and controlling method for pipe string erosion in gas drilling[J]. Acta Petrolei Sinica, 2007, 28 (6) : 129–132. |
| [6] |
张晓东, 贾国超, 吴臣德. 空气钻井钻具冲蚀磨损机理的分析[J].
西南石油大学学报:自然科学版, 2009, 31 (2) : 139–142.
Zhang Xiaodong, Jia Guochao, Wu Chende. Mechanism analysis of BHA erosion wear in air drilling[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2009, 31 (2) : 139–142. |
| [7] | 赵业荣, 孟英峰, 雷桐, 等. 气体钻井理论与实践[M]. 北京: 石油工业出版社, 2007 : 5 -7. |
| [8] |
孟英峰, 严俊涛, 沈华, 等. 华北ND1区块气体钻井地层适应性评价[J].
天然气工业, 2013, 33 (5) : 86–91.
Meng Yingfeng, Yang Juntao, Shen Hua, et al. Assessment of formation adaptability in gas drilling in Block ND1, north China[J]. Natural Gas Industry, 2013, 33 (5) : 86–91. |
| [9] |
万里平, 孟英峰. 气基流体欠平衡钻井腐蚀/冲蚀研究现状及进展[J].
天然气工业, 2007, 27 (6) : 64–66.
Wan Liping, Meng Yingfeng. Status quo and achievement made in corrosion/erosion behavior study for gas-based fluid drilling[J]. Natural Gas Industry, 2007, 27 (6) : 64–66. |
| [10] |
温诗铸. 材料磨损研究的进展与思考[J].
摩擦学学报, 2008, 28 (1) : 1–5.
Wen Shizhu. Research progress on wear of materials[J]. Tribology, 2008, 28 (1) : 1–5. |
| [11] | Orszag S A, Yakhot V, Flannery W S, et al. Renormalization group modeling and turbulence simulations[C]. Tempe, Arizona:International Conference on Near-Wall Turbulent Flows, 1993. |
| [12] |
林楠, 兰慧清, 崔钺, 等. 冲蚀角度和弯头几何尺寸对冲蚀磨损的影响研究[J].
科学技术与工程, 2013, 13 (18) : 5135–5140.
Lin Nan, Lan Huiqing, Cui Yue, et al. Effects of incidence angle and geometry of elbows on the erosion[J]. Science Technology and Engineering, 2013, 13 (18) : 5135–5140. |
| [13] | 张嗣伟. 橡胶磨损原理[M]. 北京: 石油工业出版社, 1983 : 63 . |
| [14] | Edwards J K, McLaury B S, Shirazi S A. Evaluation of alternative pipe bend fittings in erosive service[C]. MA Boston:ASME 2000 Fluids Engineering Division Summer Meeting, 2000. |
| [15] | Edwards J K, McLaury B S, Shirazi S A. Supplementing a CFD code with erosion prediction capabilities[C]. Washington DC:ASME 1998 Fluids Engineering Division Summer Meeting, 1998. |
| [16] | Haugen K, Kvernvold O, Ronald A, et al. Sand erosion of wear-resistant materials:erosion in choke valves wear[J]. Wear, 1995, 186-187 (1) : 179–188. |
| [17] | Salama M M, Venkatesh E S. Evaluation of API RP 14E erosional velocity limitations for offshore gas wells[C]. SPE 4485, 1983. |
| [18] | Nokleberg L, Sontvedt T. Erosion of oil & gas industry choke valves using computational fluid dynamics and experiment[J]. Heat and Fluid Flow, 1998, 19 (6) : 636–643. DOI:10.1016/S0142-727X(98)10039-5 |
| [19] | McLaury B S, Wang J, Shirazi S A, et al. Solid particle erosion in long radius elbows and straight pipes[C]. SPE 38842, 1997. |
| [20] |
郝贠洪, 李永. 风沙环境下钢结构涂层低角度冲蚀特性研究[J].
摩擦学学报, 2013, 33 (4) : 343–348.
Hao Yunhong, Li Yong. Erosion-behavior of the coating on steel structure eroded at low erosion-angle in sandstorm[J]. Tribology, 2013, 33 (4) : 343–348. |
| [21] | 林铁军.气体钻井钻柱失效机理研究[D].成都:西南石油大学, 2009. |
| [22] | Finnie I. Erosion of surfaces by solid particles[J]. Wear, 1960, 3 (2) : 87–103. DOI:10.1016/0043-1648(60)90055-7 |
| [23] | Saffman P G. The lift on a small sphere in a slow shear flow[J]. Joural of Fluid Mechanics, 1965, 22 (2) : 385–400. DOI:10.1017/S0022112065000824 |
| [24] | 董刚.材料的冲蚀行为及机理研究[D].杭州:浙江工业大学, 2004. |
 2014, Vol. 36
2014, Vol. 36

