2. 中国石油勘探开发研究院, 北京 海淀 100083
2. Research Institute of Petroleum Exploration and Development, PetroChina, Haidian, Beijing 100083, China
稠油油水相对渗透率数据是稠油油藏开发过程中进行水驱油效率预测、产水动态分析和油藏数值模拟等不可缺少的重要资料[1-5],其可靠性将对油田开发参数计算结果产生影响。然而,稠油油水相对渗透率实验过程中水相相渗曲线抬不起头、油水相渗曲线异常等问题一直困扰着油田开发实验人员,也给相对渗透率曲线的正确应用带来困难。
相对渗透率实验过程繁琐、数据处理过程复杂、依赖因素过多。针对油水相对渗透率实验的影响因素,前人已进行了大量工作,可以归纳为:(1) 数据测量(驱替泵精度、产油量计量、压差测量精度)误差[6];(2) 数据处理方法(数据光滑和求导)误差[7-8];(3) 实验操作条件(润湿性、应力敏感、温度、敏感性伤害、流度比、驱替速度)误差[9-13];(4) 相对渗透率计算模型和计算方法(如常规相对渗透率计算方法、考虑毛管力计算方法、驱替流体类型)误差[14-18]等。纵观以上研究结果,关于相对渗透率实验过程中死体积的处理方法没有相关叙述。}
在稠油油藏的高温相渗实验过程中,由于原油黏度较高,实验温度高,出口端计量管线长,系统管线的死体积与岩芯孔隙体积相当,当岩芯体积较小时,死体积甚至还要大于岩芯孔隙体积,死体积孔隙中水驱油规律和死体积校正方法会对实验结果产生重要影响,使用常规简单扣除管线孔隙体积的来处理死体积方法往往会使产油量计量产生较大误差,从而影响相对渗透率曲线的测试结果。
本文在实验管线中进行了3种黏度原油在不同驱替速度下的水驱油实验,发现了管线中水驱油的非活塞性和压力滞后效应,并对实验结果进行了多元回归,给出了管线中水驱油的无水采收率预测模型,提出了稠油相对渗透率实验过程死体积的校正方法。
1 实验管线中的水驱油规律 1.1 实验过程实验过程使用的管线直径为3 mm,管线孔隙体积4.92 mL,原油黏度分别为557,1 700和3 370 mPa·s。%实验前管线先饱和油,然后进行水驱油。实验结束后,用溶剂清洗管线,用比色法或色谱法确定管线中的残余油量。实验装置示意图如图 1所示,主要实验步骤如下:
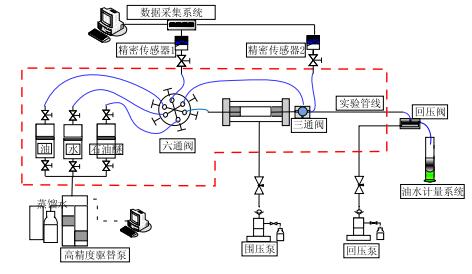 |
| 图1 实验装置示意图 Fig. 1 The devices of experiment |
(1) 实验管线饱和油。实验前先把六通阀和三通换向阀切换到实验管线流程,关闭水中间容器,打开油中间容器,启动驱替泵,对管线饱和油。
(2) 死体积管线残余油清洗。管线饱和油后,关闭油中间容器,打开石油醚中间容器,在三通阀处放空,清洗死体积管线中原油,用氮气吹干。
(3) 实验管线水驱油。流程切换到实验管线,进行水驱油实验,直到含水达到99%以上,实验过程记录驱替时间、压力、产油量、产水量。
(4) 管线残余油测定。实验结束后,用溶剂清洗实验管线,用比色法或色谱法确定实验管线中的残余油量。
(5) 重复步骤(1)~(4)至所有方案实验完成。
(6) 进行岩芯油水相渗实验。把实验流程切换到岩芯夹持器流程,分别进行岩芯饱和水、油驱水造束缚水和水驱油相渗实验。
1.2 不同黏度原油水驱无水采收率和最终采收率变化规律图 2为驱替速度为2.0 mL/min下得到的3种不同黏度的原油在管线中的水驱采收率曲线(${\mu}_{\rm{o}}$-原油黏度,mPa·s)。图 2中早期直线段为见水前的无水产油期,中期为两相流阶段,后期水平直线段为只产水不产油阶段。从图 2可以看出,在水驱速度2.0 mL/min条件下,黏度越高,两相区范围越大。
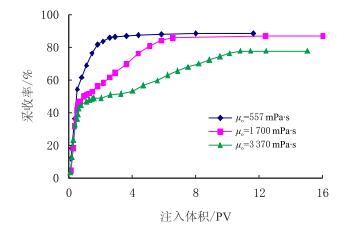 |
| 图2 不同黏度原油采收率曲线 Fig. 2 The water flooding recovery of heavy oil with different viscosity |
图 3为3种不同黏度的原油在不同水驱速度下的无水采收率变化曲线,图 4是最终采收率变化曲线。
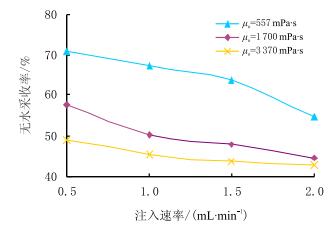 |
| 图3 不同黏度原油在不同注入速率下的无水采收率 Fig. 3 The free water recovery of oil with different viscosity at different inject rate |
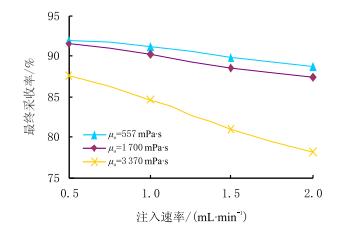 |
| 图4 不同黏度原油在不同注入速率下的最终采收率 Fig. 4 The ultimate recovery of oil with different viscosity at different inject rate |
实验结果表明,稠油在实验管线中的无水采收率和最终采收率随驱替速度提高和原油黏度增加都有降低趋势。3种黏度的原油在实验管线中的无水采收率变化范围为70.91%~42.72%,最终采收率变化范围92.00%~78.18%。由此可见,稠油在管线中的水驱流动不仅存在两相流,而且最终采收率也不能达到100.00%。因此,根据累计产油量简单扣除管线孔隙体积来校正产油量,将会使相对渗透率实验结果严重偏离实际流动情况。
1.3 测量压力滞后现象相对渗透率实验理论上应该测量的是不同时间岩芯出口端的压差、产液量和产油量,实际上,由于出口端管线死体积的存在,测量的压力是岩芯两端真实的压差,但计量的产油体积是从岩芯出口端经过一定时间运移后到达计量管线出口的产油量,计量的压力和产油量不同步。相对渗透率实验过程的测量压力滞后现象可用图 5中的压力曲线、产油量曲线来进行解释(t0,t1-0时刻和1时刻对应的时间,min;p0,p1-0时刻和1时刻的压力,MPa)。
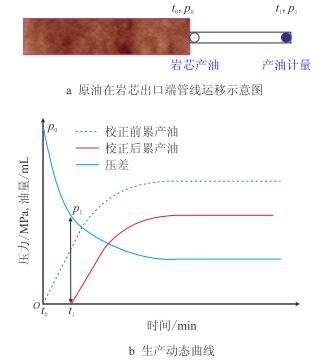 |
| 图5 恒速法测量油水相对渗透率生产动态示意图 Fig. 5 The schematic diagram of production performance |
假设时间为t0时的压力为p0,这时岩芯端面开始产油,当时间为t1时,岩芯端面的产油运移到计量管线出口端,这时压力降为p1。当产油量曲线进行死体积校正后,t1时刻的产油量为0,对应岩芯端面刚开始产油时刻,这时对应的压力为p1,与岩芯刚开始产油时的压力p0不对应,即校正死体积后的产油量和压力不同步。因此,当产油量通过死体积校正到岩芯出口端后,压力也应根据管线孔隙体积和驱替速度进行相应的校正。
2 稠油相渗实验过程死体积处理方法 2.1 管线中水驱油无水采收率预测模型管线中水驱油实验结果证实,当稠油黏度很高时,管线中的水驱油流动为非活塞式驱替,无水采收率和最终采收率主要受驱替速率和原油黏度的影响。通过对实验数据的分析和多元函数拟合,得到管线中无水采收率的预测模型为
| $ \eta = {q^{ - 0.15}}\left( {117.67 - 8.64\ln \mu _{\rm{o}} } \right) $ | (1) |
式中:${\eta}$-无水采收率,%;q-驱替速率,mL/min。
2.2 稠油相渗管线死体积处理方法在稠油相渗实验中处理管线死体积建议采用综合处理法,其具体步骤如下:(1) 根据驱替速率和原油黏度,计算出无水采收率,确定管线死体积中的无水采油量。(2) 首次修正累积产油量。首先在累积产油量中直接减去计算出的无水采油量。(3) 再次修正累积产油量。用管线死体积减去无水采油量和管残油量得到管线中两相流时采出的管线死油量,采用比例减去法减去两相流时采出的死油量,最终得到修正后的累积产油量。(4) 压力滞后修正。对压力滞后校正可采用两种方法,一种是把校正后的累产油曲线向前平移经过坐标原点;另一种方法是用管线死体积中的无水采油量除以驱替速率得到校正的时间$\Delta t$,把压力曲线向后平移$\Delta t$,使压力和产油量同步。
图 6为死体积处理方法校正前后计算的热水驱稠油相渗曲线($K_{\rm{ro}}$,$K_{\rm{rw}}$-油,水相对渗透率,%)。
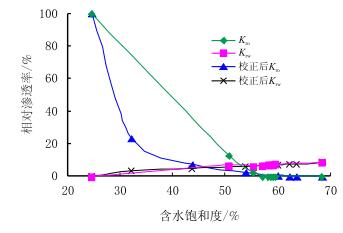 |
| 图6 死体积处理方法校正前后相对渗透率曲线 Fig. 6 The comparison of relative permeability before and after using new correction method |
从图 6可知:(1) 管线中的非活塞驱对油相相对渗透率影响较明显;(2) 水相相对渗透率差别不大;(3) 由于实验数据已对管线残余油进行了扣除,所以计算的相对渗透率曲线端点一致。
3 结论(1) 发现了稠油油水相对渗透率实验过程管线死体积中水驱油的非活塞性和压力滞后现象。
(2) 根据实验管线中的水驱油实验数据,采用多元回归建立了稠油在管线中的无水采收率预测模型。
(3) 提出了考虑稠油油水相对渗透率实验过程管线死体积中的非活塞性和压力滞后效应的死体积处理方法。
| [1] | 岳清山, 沈德煌. 有关稠油油藏驱油效率的讨论[J]. 特种油气藏, 2002, 9 (1) : 26–29. |
| [2] | 蒋庆坦, 陈万珍. 利用相对渗透率资料预测油藏动态的研究[J]. 石油勘探与开发, 1985, 12 (1) : 38–46. |
| [3] | 常毓文. 高温相对渗透率曲线在热采数值模拟研究中的应用[J]. 石油勘探与开发, 1991, 18 (4) : 64–68. |
| [4] | 王振斌, 刘丽萍, 陈世明. 相对渗透率分析技术在葡西地区储集层产液性质解释评价中的应用[J]. 录井工程, 2006, 17 (2) : 5–7. |
| [5] | 蒋炳金, 唐海, 吕栋梁, 等. 用相对渗透率曲线研究薄层底水油藏产水规律[J]. 新疆石油地质, 2006, 27 (5) : 588–590. |
| [6] | Tao T M, Watson A T. Accuracy of JBN estimates of relative permeability:Part 1--Error analysis[J]. Old SPE Journal, 1984, 24 (2) : 209–214. |
| [7] | Tao T M, Watson A T. Accuracy of JBN estimates of relative permeability:Part 2--Algorithms[J]. Old SPE Journal, 1984, 24 (2) : 215–223. |
| [8] | 杨小平. 精确计算相对渗透率的方法[J]. 石油勘探与开发, 1998, 25 (6) : 63–66. |
| [9] |
何建民. 油水相对渗透率曲线异常影响因素探讨[J].
油气地质与采收率, 2009, 16 (2) : 74–76.
He Jianmin. Influencing factors of abnormal oil/water relative permeability curve[J]. Petroleum Geology and Recovery Efficiency, 2009, 16 (2) : 74–76. |
| [10] |
李俊键, 姜汉桥, 陈民锋, 等. 聚合物驱相对渗透率曲线及影响因素微观模拟[J].
西南石油大学学报:自然科学版, 2009, 31 (4) : 122–126.
Li Junjian, Jiang Hanqiao, Chen Minfeng, et al. Microscopic modelling of polymer flooding relative permeability curve and its influence factors[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2009, 31 (4) : 122–126. |
| [11] |
邓勇, 彭光明. 应力敏感储层相对渗透率计算方法研究[J].
西南石油大学学报:自然科学版, 2011, 33 (2) : 95–98.
Deng Yong, Peng Guangming. A calculation method for relative permeability curve of stress sensitive[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2011, 33 (2) : 95–98. |
| [12] | 周光辉, 王建设. 温度影响油水相对渗透率的机理[J]. 石油学报, 1992, 13 (3) : 62–70. |
| [13] | 刘宝良, 沈德煌, 张勇, 等. SY/T 6315-2006稠油油藏高温相对渗透率及驱油效率测定方法[S].北京:石油工业出版社, 2006. |
| [14] | 李克文, 沈平平, 秦同洛. 考虑毛管压力时计算油水相对渗透率的新方法[J]. 力学与实践, 1994, 16 (2) : 46–48. |
| [15] | 石京平, 李凤琴, 曹维政, 等. 非稳态法测定聚合物驱相对渗透率曲线[J]. 大庆石油地质与开发, 2001, 20 (5) : 53–64. |
| [16] | 洪世铎. 华北裂缝油藏岩石相对渗透率的计算[J]. 石油大学学报:自然科学版, 1989, 13 (6) : 16–19. |
| [17] |
陈田勇, 毛鑫, 刘仕银, 等. 利用分形理论计算相对渗透率曲线--以南襄盆地双河油田核桃园组六油组为例[J].
石油与天然气地质, 2012, 33 (4) : 578–581.
Chen Tianyong, Mao Xin, Liu Shiyin, et al. Fractal theory-based calculation method of relative permeability curves--A case study from the Hetaoyuan Formation in Shuanghe Oilfield, Nanxiang Basin[J]. Oil & Gas Geology, 2012, 33 (4) : 578–581. |
| [18] |
柯式镇. 模拟退火算法在基于非稳态驱替实验的相对渗透率计算中的应用[J].
中国石油大学学报:自然科学版, 2006, 30 (4) : 35–37.
Ke Shizhen. Application of simulation annealing algorithm in calculation of relative permeability from unsteadystate displacement experimental data[J]. Journal of China University of Petroleum, 2006, 30 (4) : 35–37. |
 2014, Vol. 36
2014, Vol. 36

