2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
DH气藏为块状底水气藏,储层物性好,砂体平面分布广且连通 性好,开采速度快,产水量逐年上升。目前该气藏处于开采的 中后期,产水量较大,大部分生产区块见水,调整生产方案势在 必行。为此,需要开展DH水驱砂岩气藏提高采收率对策研究,而 残余气饱和度是研究水驱波及系数、确定水驱气藏最终采收率和 制定开发技术对策所需的重要参数。
在底水或边水水驱气藏生产过程中,地层水侵入储层,排驱 和捕集孔隙中的气体。捕集的气体称为残余气,它不能自由流 动,也不能从地层中采出。残余气体积与岩样孔隙体积的比值 称为残余气饱和度。渗吸实验有助于认识残余气的产生机理, 分析残余气的各种影响因素,建立原始含气饱和度与残余气饱 和度之间的关系式,以及预测水驱气藏的残余气饱和度。
目前,测试残余气饱和度的方法主要有稳态驱替法、被动渗 吸法、单向与多向自发渗吸法和网络模拟法[1-3]。这些 方法中稳态法和自发渗吸实验测试的结果准确可靠[1],使用较 多。许多文献[2-13]指出, 残余气饱和度的影响因素主要包括: 孔喉类型、孔隙度、渗透率、流体性质、流体进入岩样的方式、 渗吸速率、岩石颗粒大小及分选程度、黏土矿物含量、原始含气 饱和度和界面张力。不同类型的碳酸盐岩的最大残余气饱和度不 同[4, 9];当砂岩中黏土含量增加或岩石颗粒粒径和分选程减 小时,残余气饱和度增大[7, 10];当岩样初始含气饱和度较小、孔 隙结构较复杂、孔隙度和孔喉较小时,残余气饱和度较大[11]。流体 性质、进入岩样的方式和岩样渗吸速率对残余气饱和度影响较小[5-6, 8]。 对于油-水系统,润湿性、界面张力对残余油饱和度的影响较大,而对于 气-水系统,润湿性、界面张力对残余气饱和度的影响较小[3]。 Ding Minghua等[2]对加拿大北部的砂岩岩样进行多向渗吸实验,从测试结果中发现最 大残余气饱和度随着岩样孔隙度的增加而减小,并且其渗透率亦有相 同的变化趋势。Suzanne K等[14]在实验中发现最大残余气饱和度随着砂 岩孔隙度的增加而增加。生如岩[12]发现残余气饱和度随着孔隙度 的增大有明显的下降趋势,当孔隙度增加10%,残余气饱和度下降10.18%; 而残余气饱和度随着渗透率增加没有明显的下降趋势,渗透率增加10倍时,残余气饱和度下降约5.23%。
本文采用单向自发渗吸实验装置测试了DH气藏水驱砂岩气藏岩样 的残余气饱和度,分析了岩样初始含水饱和度对残余气饱和度的影响及岩 样孔隙度和渗透率对最大残余气饱和度的影响。建立了DH水驱砂岩气藏原始含气饱和度与 残余气饱和度之间的关系式,根据关系式计算出该气藏的残余气 饱和度,将该残余气饱和度用于确定水驱气藏的体积波及系数, 并为DH气藏提高采收率对策研究提供了基础实验研究成果。
1 实验方法及实验准备 1.1 单向自发渗吸实验气藏中几乎所有的岩样都是亲水的。自发渗吸实验利用亲水 岩样在吸水过程中的毛细管力作为渗吸动力,将水吸入岩样, 排驱孔隙中的气体。单向自发渗吸实验需要水从岩样的一个端 面吸入,气体从岩样的另一个端面排出。为满足这一条件,在 实验室条件下温度(25℃,压力0.1 MPa),将岩样垂直悬挂于 天平底端、岩样底端与地层水水面平行接触(图 1)。根据渗吸 实验之前岩样孔隙中是否饱和地层水,将实验进一步分为单向 自发渗吸第一类实验和单向自发渗吸第二类实验,后面简称一 类渗吸实验和二类渗吸实验。一类渗吸实验之前岩样不饱和地 层水,只饱和气体;二类渗吸实验之前岩样饱和了气体和地层水。
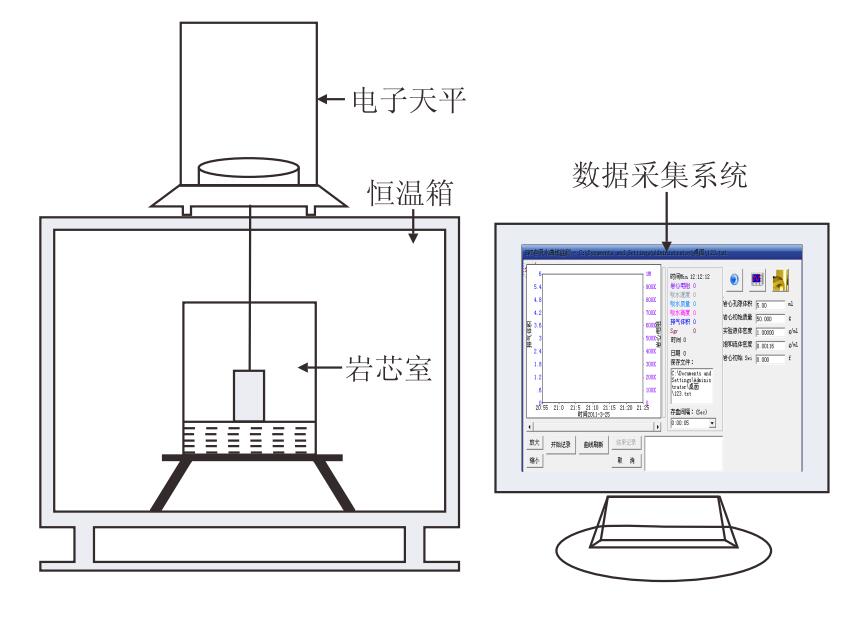 |
| 图1 自发渗吸实验装置 Fig. 1 Spontaneous imbibition experiment apparatus |
一类渗吸实验之前用烘箱烘干岩样,其初始含水饱和度为零;二类 渗吸实验之前使用离心机设置岩样的初始含水饱和度。据实验方案,同一块 岩样需要进行两次二类渗吸实验,将完全饱和地层水的岩样分别在1 000和6 000 r/min的 转速下脱水4 h可得到相应的岩样初始含水饱和度$S_{\rm{wi}}$[15],如表 1所示。 实验过程中,岩样吸水,岩样质量增加,电子天平实时记 录岩样质量并将其传入数据采集系统。数据采集系统计算并显示岩样中气体饱 和度随时间的变化,根据气体饱和度与时间的关系判断是否结束实验。 当岩样的含气饱和度不再随时间变化时停止实验。一类渗吸实验测得的 残余气饱和度称为最大残余气饱和度$S_{\rm{grm}}$[14],二类渗吸实验的结果为 残余气饱和度$S_{\rm{gr}}$。
1.2 实验岩样和地层水实验岩样选用采集到的DH气藏砂岩气藏储层岩样20块,这些岩 样的孔隙度为11.60%~22.98%,平均值为17.10%;渗透率 为3.84 573.00 mD,平均值为131.74 mD。 为减小液体对岩样造成的损害,根据水质分析报告,配制40 000 mg/L 的NaCl溶液作为实验的地层水溶液。
1.3 饱和度的计算自发渗吸实验中,岩样质量的变化是由于水的吸入和气体的排 出造成的,假设吸入水的体积等于排出气体的体积,则排出气 体的体积与岩样的质量变化满足式(1)。岩样孔隙中的 气体体积与排出气体的差值为岩样孔隙中剩余气体体积,它与 孔隙体积的比值即为气体饱和度,见式(2)。数据采集系统基 于式(1)和式(2)计算气体饱和度,并记录气体饱和度与实验 时间的关系。
岩样中排出的气体体积和岩样中气体饱和度为
| ${V_{\rm{g}}} = \frac{{\Delta m}}{{{\rho _{\rm{w}}} - {\rho _{\rm{g}}}}}$ | (1) |
| ${S_{\rm{g}}} = 1 - \frac{{{V_{\rm{g}}}}}{{{V_{\rm{p}}}}} - {S_{{\rm{wi}}}}$ | (2) |
一类渗吸实验,式(2)中岩样原始含水饱和度为零;二类渗吸实验,岩样离心之后采用式(3)计算岩样原始含水饱和度
| ${S_{{\rm{wi}}}} = 1 - \frac{{\Delta {m_{\rm{w}}}}}{{{\rho _{\rm{w}}} \cdot {V_{\rm{p}}}}}$ | (3) |
文献[5]指出,当岩样自发渗吸时,侵入水捕集并圈闭岩样孔 喉间的气体,使其不能在岩样中自由流动,也不能从岩样中产 出。实验过程中,岩样的气体饱和度随水的渗入而逐渐减小, 当减小至残余气饱和度时基本上不再变化,可认为这时的气体 饱和度就是实验岩样的残余气饱和度。
以T1-6岩样为例,说明实验过程中确定残余气饱和度的方法。作岩 样含气体饱和度与实验时间二分之一次方的曲线(图 2),从图 2可以看出,随着实验的进行,岩样中气体饱和度逐渐减小,到达一定时间后 基本上不再变化。出现明显拐点处的横坐标对应产生残余气饱和 度的时间,纵坐标对应(最大)残余气饱和度。T1-6岩样一类渗吸 实验的最大残余气饱和度$S_{\rm{grm}}$=0.362 0;二类渗吸实验初始含水饱 和度$S_{\rm{wi}}$=0.811 6时,测得残余气饱和度$S_{\rm{gr}}$=0.111 0,初始含水饱和度 $S_{\rm{wi}}$=0.501 0时,测得残余气饱和度$S_{\rm{gr}}$=0.309 0。二类渗吸实验在出现 残余气饱和度之后,由于气体的扩散导致曲线仍缓慢下降,圈闭的气 体虽然无法自由流动,但可以扩散并侵入水中,导致气体饱和度缓 慢地减小。
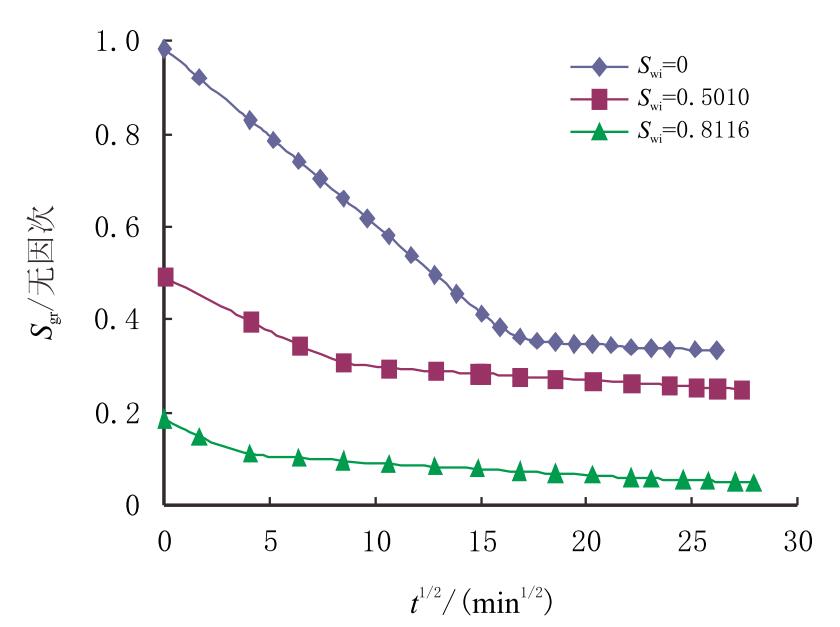 |
| 图2 T1-6岩样气体饱和度与实验时间二分之一次方的关系 Fig. 2 Relationship between gas saturation and the square root of experimental time |
实验测试了DH气藏水驱砂岩气藏20块岩样的(最大)残余气饱和度见表 1。 实验结果表明岩样一、二类渗吸实验的(最大)残余气饱 和度在0.056 8$\sim$0.479 0,其中一类渗吸实验的最大残 余气饱和度$S_{\rm{grm}}$在0.327 0$\sim$0.479 0。
| 表1 DH气藏水驱砂岩气藏岩样的(最大)残余气饱和度 Table 1 (Max)residual gas saturation results of samples in water-driven reservoir of DH gas reservoir |
通过分析表 1中的数据,发现岩样的残余气饱和度随着岩样初始 含水饱和度的增加而减小。将所有岩样二类渗吸实验的原始含气 饱和度与残余气饱和度数据绘制在图 3中,拟合出满足两者关系 的关系式(4)。由于原始含气饱和度与初始含水饱和度有着 直接的关系,因此,岩样的初始含水饱和度是影响残余气饱和 度的重要因素。
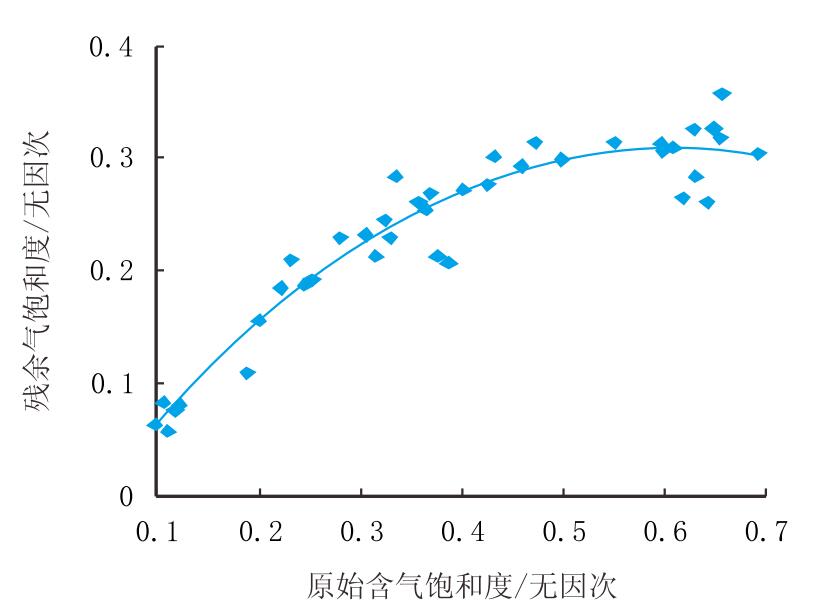 |
| 图3 DH气藏水驱砂岩气藏岩样的原始含气饱和度与残余气饱和度的关系 Fig. 3 Relationship between initial gas saturation and residual gas saturation in water-driven reservoir of DH gas field |
拟合得到的计算DH气藏残余气饱和度的公式为
| ${S_{gr}} = - 0.9902S_{gi}^2 + 1.1864{S_{gi}} - 0.0455$ | (4) |
DH气藏水驱砂岩气藏的原始平均含气饱和度为$S_{\rm{gi}}$=0.773 5,通过 式(4)计算出气藏的残余气饱和度为$S_{\rm{gr}}$=0.279 7。
3.2 最大残余气饱和度与孔渗的关系图 4和图 5给出的是最大残余气饱度($S_{\rm{grm}}$)和岩石物性间的关系。 随着孔隙度的增大,最大残余气饱和度稍微有所增加;而渗透率增 大时,最大残余气饱和度几乎没有变化。从图 4和图 5可以看出,残 余气饱和度和岩石物性孔隙度和渗透率的关联性不强,如用一次函 数拟合,相关系数分别只有0.215 4和0.015 6。
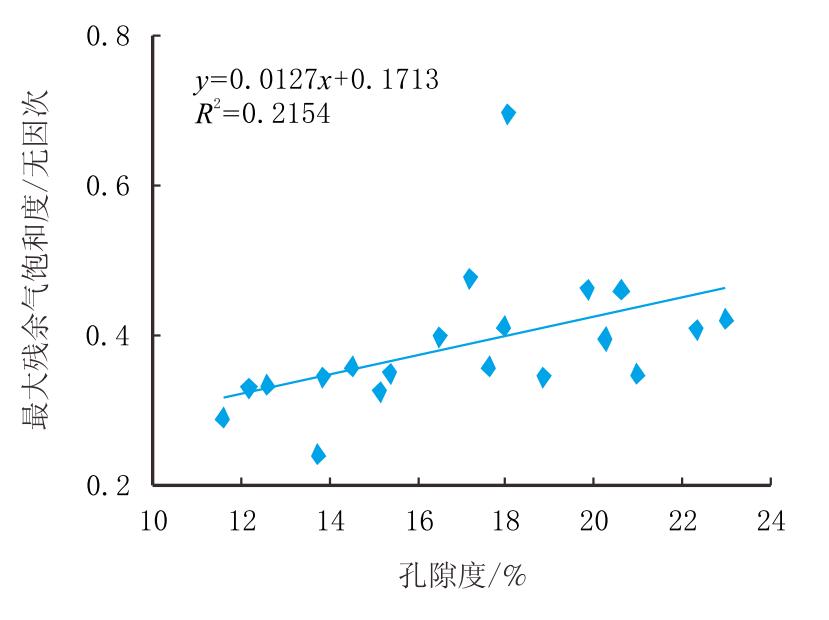 |
| 图4 最大残余气饱和度与孔隙度关系图 Fig. 4 Relationship between max residual gas saturation and porosity |
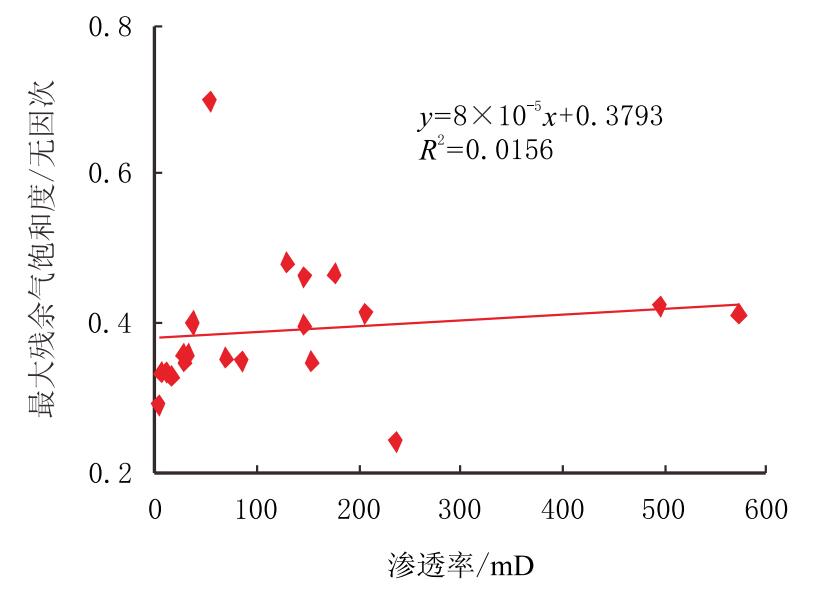 |
| 图5 最大残余气饱和度与渗透率关系图 Fig. 5 Relationship between max residual gas saturations and permeability |
一般认为,岩样的孔隙度和渗透率是影响最大残余 气饱和度的主要因素[4, 7, 9-11],因此,大多数研究人员试图 去寻找岩石孔隙度和渗透率与最大残余气饱和度之间的关系式,然而,本次测试 实验发现渗透率、孔隙度与最大残余气饱和度之间的关联性不强, 这可能是最大残余气饱和度不仅受孔喉大小控制,还受孔喉大小分 布影响而造成的。
4 实验与理论结果对比分析及应用为了建立残余气饱和度与原始含气饱和度之间的关系式,许多学者 进行了大量的研究工作。Land C S[13]将Holmgren、Dyes、Kyte、Dardaganian 和Crowell等[8, 16-18]的实验数据绘制成曲线,发现同一岩样残余 气饱和度的倒数与原始含气饱和度的倒数之差接近一个常数,据此拟合 出计算两者关系的经验公式。同时也发现了残余气饱和度随着初始含 气饱和度的增加而增加。Land给出的残余气饱和度的计算公式为
| ${S_{{\rm{gr}}}} = \frac{{{S_{{\rm{gi}}}}}}{{1 + (1/{S_{{\rm{grm}}}} - {S_{{\rm{grm}}}} - 1){S_{{\rm{gi}}}}}}$ | (5) |
Agarwal R G[19]考虑了岩样基本物性对残余气饱和度的影响,测试了3类 物性不同的岩样(非胶结砂岩、胶结砂岩和碳酸盐岩)的残余气饱和度 ,将实验数据用线性回归方法建立了计算这3类岩样残余气饱和度的经 验公式。这里只给出计算胶结砂岩残余气饱和度的经验公式
| ${S_{{\rm{gr}}}} = - 0.0063869116S_{{\rm{gi}}}^2 + 0.80841168{S_{{\rm{gi}}}}$ | (6) |
将二类渗吸实验的原始含气饱和度代入式(5)和式(6)中计算 出所有实验岩样的残余气饱和度,并将计算结果与测试结果进行对比。结 果表明:实验测试结果与Land模型吻合较好,而与Agarwal模型的吻合程 度比较差(图 6)。Land模型可以用于预测DH气藏残余气饱和度值。
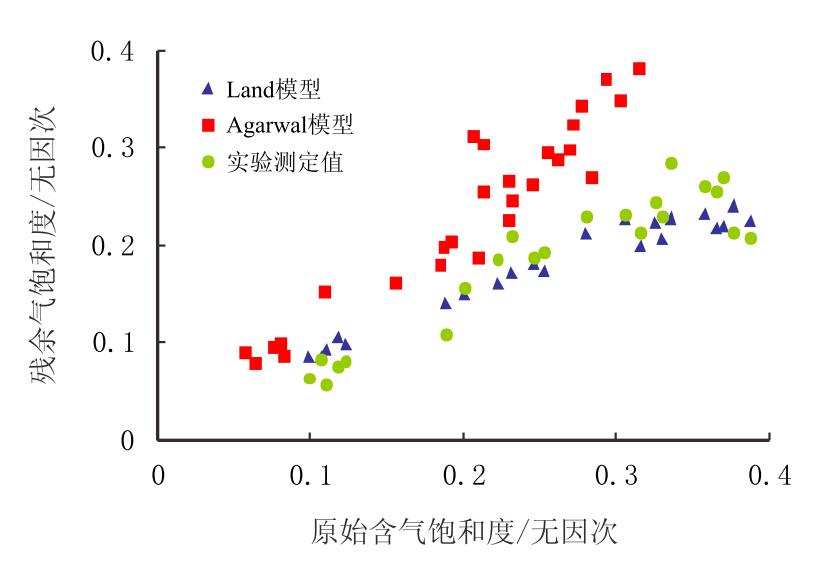 |
| 图6 实验测试结果与经验模型计算结果对比 Fig. 6 Comparison experimental results with emprical mode results |
目前,DH气藏已进入产量递减阶段,需要通过研究确定气藏的体积波及系数,并结合其他研究提出针对性的下一步开发技术对策。DH气藏孔隙体积 ${V_{\rm{pr}}}$=185 518 86 m$^3$,原始含水饱和度$S_{\rm{wi}}$=0.226 5,根据Carter R D等[20]提出的水侵量计算方法得到目前气藏的累计水侵量 $W_{\rm{e}}$=584 769 9 m$^3$, 气藏累计产水量$W_{\rm{p}}$=246 57 m$^3$,实验测定的DH气藏的残余气饱和度$S_{\rm{gr}}$=0.279 7。根据 Stoian等[12]提出的体积波及系数计算公式${E_{\rm{v}}} = \left( {{W_{\rm{e}}} - {B_{\rm{w}}} \times {W_{\rm{p}}}} \right)/{V_{\rm{pr}}}/\left( {1 - {S_{{\rm{wi}}}} - {S_{{\rm{gr}}}}} \right)$,得到目前气藏水驱体积波及系数${E_{\rm{v}}}$=0.635 6,说明气藏已 经大面积水淹,难以采用打新井的方法提高气藏采收率。因此,采用的封堵水层和 排水采气是提高该水驱气藏采收率的有效方法。
5 结 论根据单向自发渗吸实验结果,建立了DH水驱砂岩气藏原始含 气饱和度与残余气饱和度之间的二次关系式,得到该气藏残余气饱和 度为0.279 7。
岩样初始含水饱和度是影响残余气饱和度的重要因素,而 孔隙度、渗透率对最大残余气饱和度的影响较小。
实验测试结果与Land模型比较吻合,而与Agarwal模型的 吻合比较差。说明了Land模型也可以用于预测DH气藏的残余气饱和度。} \jielun{DH气藏目前的体积波及系数为0.635 6,气藏已经大面积水淹,难以采 用打新井的办法进一步气藏的采收率。
符 号 说 明${S_{{\rm{grm}}}}$--最大残余气饱和度,无因次; ${S_{{\rm{gr}}}}$--残余气饱和度,无因次; ${V_{\rm{g}}}$--排出气体体积,cm$^3$; $\Delta m$-- 岩样渗吸过程中质量增加量,g; ${\rho _{\rm{w}}}$-- 地层水密度,g/cm$^3$; ${\rho _{\rm{g}}}$-- 气体密度,g/cm$^3$; ${S_{{\rm{g}}}}$-- 气体饱和度,无因次; ${V_{\rm{p}}}$-- 岩样孔隙体积,cm$^3$; ${S_{{\rm{wi}}}}$-- 岩样原始含水饱和度,无因次; $\Delta {m_{\rm{w}}}$-- 建初始含水饱和度前后岩样质量减少量,g; t-- 实验时间,min; ${S_{{\rm{gi}}}}$-- 原始含气饱和度,无因次; K-- 渗透率,mD; $\phi$-- 孔隙度,{\percent}; $E_{\rm{v}}$-- 水体波及系数,无因次; $W_{\rm{e}}$-- 累计水侵量,m$^3$; $B_{\rm{w}}$-- 地层水体积系数,m$^3$/m$^3$; $W_{\rm{p}}$-- 累计产水量,m$^3$; $V_{\rm{pr}}$-- 气藏孔隙体积,m$^3$。
| [1] | Mulyadi H, Amin R, Kennaird T, et al. Measurement of residual gas saturation in water-driven gas reservoirs:comparison of various core analysis techniques[C]. SPE 64710, 2000. |
| [2] | Ding Minghua, Apostolos K. Residual gas saturation investigation of a carbonate reservoir from western Canada[C]. SPE 75722, 2002. |
| [3] | Holtz M H. Residual gas saturation to aquifer influx:a calculation method for 3-D computer reservoir model construction[C]. SPE 75502, 2002. |
| [4] | Keelan D K, Pugh V J. Trapped-gas saturation in carbonate formations[J]. SPE Journal, 1975, 15 (2) : 149–160. |
| [5] | Geffen T M, Parrish D R, Haynes G W, et al. Efficiency of gas displacement from porous media by liquid flooding[J]. Journal of Petroleum Technology, 1952, 4 (2) : 29–38. |
| [6] | Crowell D C, Dean G W, Loomis A G. Efficiency of gas displacement from a water-drive reservoir. Michigan:University of Michigan Library[M]. 1966 . |
| [7] | Jerauld G R. Prudhoe bay gas/oil relative permeability[J]. SPE Reservoir Engineering, 1997, 12 (1) : 66–73. |
| [8] | Kyte J R, Stanclift R J, Stephan S C, et al. Mechanism of water flooding in the presence of free gas[J]. Petroleum Transactions, AIME, 1956, 207 : 215–221. |
| [9] | Batycky J P,Irwin D D,Fish R M. Trapped gas saturation in leduc-age reservoirs[C]. SPE 95-75, 1995. |
| [10] | Hamon G, Suzanne K, Billiotte J, et al. Field-wide variations of trapped gas saturation in heterogeneous sandstone reservoirs[C]. SPE 71524, 2001. |
| [11] | Holtz M H, John A, Katherine G, et al. Petrophysical characterization of permian shallow-water dolostone[C]. SPE 75214, 2002. |
| [12] |
生如岩. 水驱砂岩气藏残余气饱和度试验研究[J].
石油天然气学报, 2010, 32 (4) : 105–107.
Sheng Ruyan. Experimental study on residual gas saturation of water-flooded sandstone gas reservoirs[J]. Journal of Oil and Gas Technology, 2010, 32 (4) : 105–107. |
| [13] | Land C S. Calculation of imbibition relative permeability for two-and three-phase flow from rock properties[J]. SPE Journal, 1968, 8 (2) : 149–156. |
| [14] | Suzanne K, Hamon G, Billiotte J. Experimental relationships between residual gas saturation and initial gas saturation in heterogeneous sandstone reservoirs[C]. SPE 84038, 2003. |
| [15] | Kantzas A, Ding Minghua, Jone L. Residual gas saturation revisited[C]. SPE 59782, 2000. |
| [16] | Holmgren C R, Morse R A. Effect of free gas saturation on oil recovery by water flooding[J]. Journal of Petroleum Technology, 1951, 3 (5) : 135–140. |
| [17] | Dyes A. B. Production of water-driven reservoirs below their bubblepoint[J]. Journal of Petroleum Technology, 1954, 6 (10) : 31–35. |
| [18] | Dardaganian S G. The displacement of gas by oil in the presence of connate water[D]. Texas:A. & M. College of Texas, 1957. |
| [19] | Agarwal R G. Unsteady-state performance of water-drive gas reservoirs[D]. Texas:Texas A&M University, 1967:46-59. |
| [20] | Carter R D, Tracy G W. An improved method for calculating water influx[J]. Petroleum Transactions, AIME, 1960, 219 : 415–417. |
| [21] | Stoian E, Telford A S. Determination of natural gas recovery factors[J]. Journal of Canadian Petroleum Technology, 1966, 5 (3) : 115–129. |
 2014, Vol. 36
2014, Vol. 36
