金融是现代经济的核心,金融市场占据着整个市场经济体系的关键地位,而金融危机的多米诺骨牌效应及金融本身存在的高风险性,使金融体系的安全、高效、稳健运行对经济全局的平稳与发展具有举足轻重的作用。股票市场是金融投资的重要组成部分,股市风险的波动直接影响金融体系的稳定与发展[1-4]。
风险价值(Value at Risk)模型(以下简称为VaR)是金融风险评估的重要工具[5-9],已成为许多金融机构和银行衡量市场风险的一种标准方法。虽然VaR模型能够在一定程度上反映市场的风险,但是VaR的计算方法还是存在一定缺陷,比如:它不能有效地度量尾部事件发生时可能遭受的平均损失的程度。条件风险价值(Conditional Value at Risk)模型(以下简称为CVaR)被大量研究人员认为是一种相比VaR更为有效的风险度量技术[10-13],有效地解决了尾部风险的度量问题,适应性更强。二者比较,VaR概念简单、计算方便,能够迅速反映一个收益序列在一定时间内面临的市场风险,而CVaR的判断相对而言比较保守。
当前,国内外对于VaR和CVaR模型的研究,主要集中在如何对VaR模型进行改进与修正,以及如何在商业银行和金融行业进行风险度量,但是极少将这两个模型应用于股市领域的风险度量。笔者选取了沪深300指数的收盘价数据,创新性地以股市风险度量的视角对VaR模型和CVaR模型进行深入的实证分析,比对两种模型用于股票市场风险度量的特点,这对股市风险新型度量方法的研究具有较强的理论以及实践意义。
1 VaR与CVaR理论模型 1.1 VaR模型VaR是指资产在确定目标时间段和置信水平下预期的最大资产损失。其表达式为:
| $ P(\Delta P > {\rm{VaR}}) = 1 - C $ | (1) |
其中C为置信水平,为持有期内资产损失。从表达式(1)可以看出,计算VaR需要三个条件:确定一个合适的置信水平C,资产收益率序列的分布,确定资产持有期。如果假定资产收益率服从正态分布N(µ, σ2),那么就可以得到VaR的计算公式:
| $ {\rm{VaR}} = {{\rm{w}}_0}{{\rm{z}}_\alpha }\sigma \sqrt {\Delta t} $ | (2) |
其中w0代表初始资产值,△t为资产持有期。已有研究表明,大部分场景下金融市场收益序列的分布并不是正态分布,所以研究中也常常会使用t分布、GED分布、混合正态分布等来计算VaR值。
1.2 CVaR模型CVaR是指在一定时期内资产损失超过VaR值的平均值,也叫期望损失。在VaR值已知的条件下,CVaR表示资产损失大于该值条件下的期望损失。假设X表示资产损失,CVaR值就是在X>VaR的条件下计算X的期望值,用数学表达式即为:
| $ {\rm{CVaR}} = {\rm{E}}[X/(X > {\rm{VaR}})] $ | (3) |
从表达式(3)可以看出,CVaR本质上是相对于VaR的一个条件表达式。CVaR的优势在于:CVaR是尾部损失的平均值,不仅仅是一个简单的分位点,CVaR的计算需要把所有大于VaR的损失都考虑进来,这样CVaR就能充分度量尾部损失。
已有研究证明CVaR具有次可加性的性质,即对于两个不同的资产A、B,总是可以满足CVaR(A+B) ≤ CVaR(A) + CVaR(B)。从表达式来看,CVaR是一个具有一致性的风险统计量,而且它还是一个凸性的风险统计量,经由改良能够找到基于CVaR的投资组合存在的最小风险解。
1.3 VaR与CVaR的理论比较 1.3.1 VaR的特点VaR虽然能够在一定程度上反映出市场的风险,但是VaR的计算方法还是存在一定缺陷,主要具有以下缺点:尾部损失测量不够充分;不具备次可加性;不具备凸性性质。首先,VaR得到的只是一个闭值,只能以较大的几率保证损失不会超过这个分位数,但是对于极端事件产生的风险控制明显不足;其次,不服从次可加性,这样就不能反映出投资组合分散风险的特点;最后,由于VaR不具备凸性性质,如果基于VaR对投资组合进行优化,这样可能造成存在多个局部极值的情况出现,很难实现整体最优。
1.3.2 CVaR的特点CVaR被大量研究人员认为是一种相比VaR更为有效的风险度量技术,它的优势主要有:一方面,更加科学地度量了尾部风险。尾部风险的损失如果估计不足,很容易造成由极端事件带来的不可承受的经济损失,从而带来严重的后果,而CVaR有效地解决了尾部风险的度量问题。另一方面,适应性更强。因为CVaR具有次可加性和凸性,所以CVaR的求解可以采用凸组合来规划求解。实际应用中要结合具体场景选择VaR还是CVaR来进行风险度量。
2 基于VaR与CVaR方法的沪深300指数风险实证对比分析 2.1 沪深300指数收益率波动特征分析 2.1.1 数据收集本研究的指标原始数据主要来源于wind数据库,选取的样本数据是2002年1月7日到2017年8月17日沪深300指数的每日收盘价,一共3 788个交易日,其间包括了2007年和2015年两次股灾事件,而且还有2008年全球金融危机,样本数据涵盖了股票市场的完整发展周期,具有很大研究价值。通过收盘价数据计算对数收益率序列来反映股价序列的波动性,对数收益率计算公式采用:xt = ln pt − ln pt−1,xt表示t时刻的收益率,pt表示t时刻的收盘价。实证分析采用软件为Eviews 8.0。图 1给出了收益率序列的时序图。
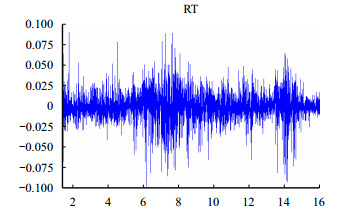 |
| 图1 收益率序列时序图 |
从图 1可以看出,日收益率序列的波动是随机过程,而且波动具有很明显的聚集效应。在2002年至2006年以及2009年至2014年这两个时间区间内,股票市场的波动比较平静,因为日收益率基本在−0.025至0.025的范围内波动,具有相当小的正负收益率。但是在2007年至2008年以及2014年至2015年这两个时间段内,市场的波动剧烈,因为日收益率基本在−0.075至0.075的范围内波动,具有相当大的正负收益率。
2.1.2 描述性统计分析一般认为正态分布的峰度系数为3,偏度系数为0,峰度系数可以呈现数据分布的走势变化,偏度系数可以呈现数据分布的形态。偏度系数是一个特征数,表示分布与对称性偏差程度。偏度系数为0时,分布左右对称;大于0时,即重尾在右侧时,分布为右偏;小于0时,即重尾在左侧时,分布左偏。数据分布在峰度系数高于3的条件下体现出尖峰厚尾特征,数据分布在峰度系数等于3的条件下与正态分布类似。
对数据分布的正态性进行检验有很多种方法,其中比较常用的有Jarque-Bera检验方法。Jarque-Bera检验是用于总体分布的正态性检验的一种方式,检验基于这样的假设:若样本来自正态总体,那么样本数据分布的偏度S =0,峰度K=3。图 2给出了收益率序列的相关描述统计量。
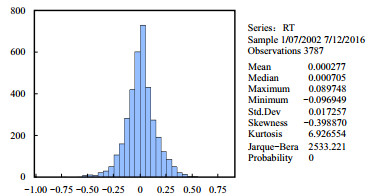 |
| 图2 收益率序列描述统计量 |
从图 2可知,收益率序列的平均值为0.000 27,所以长期看来股市收益率并不高,数据在标准差为0.017 2、偏度系数为−0.398 8(小于0)的条件下分布左偏,重尾在左侧;数据在峰度系数为6.926 5(大于3)的条件下呈现出尖峰厚尾特征。此外,P值在Jarque-Bera统计量为2 533.221的条件下,相应的检验值为0.000,得出收益率序列不服从正态分布,所以拒绝在5%的显著水平下收益率序列服从正态分布的原假设。
基于QQ图基本理论,当QQ图接近于1条直线时,那么认为该数据服从正态分布;如果QQ图下端左偏离直线或上端右偏离直线,那么认为数据分布表现出厚尾特征。图 3给出了收益率序列的QQ图。从图 3可以看出,直线代表收益率序列为正态分布的分布情况,曲线代表收益率真实分布情况。曲线上端和下端与正态分布的偏差越来越大,说明收益率序列具备显著的厚尾特征。
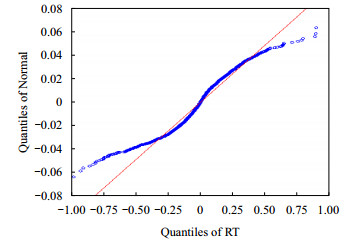 |
| 图3 收益率序列 QQ 图 |
对时间序列数据进行平稳性检验是进行GARCH建模的前提,笔者在模型变量的单位根检验上采用ADF单位根检验法,且假设起码有一个单位根存在于序列。假如在检验中证实序列是平稳的,则拒绝原假设;否则原假设成立,即序列是不平稳的。基于图 1的时序图,对ADF检验形式采用None,即无趋势项和截距项,得到检验结果见表 1。检验结果表明:ADF检验统计量为−59.833,检验P值为0.000,结果表明收益率序列平稳,所以在1%的显著水平下拒绝存在一个单位根的原假设。
| 表1 收益率序列的平稳性检验 |
首先对序列的相关性进行检验,序列的相关系数AC和偏相关系数PAC见表 2。从表 2可知,Q统计量对应的P值均低于0.1,因此在10%的显著水平下拒绝序列不存在自相关的原假设,说明收益率序列具有自相关关系。
| 表2 序列的相关性检验数值表 |
通过普通最小二乘方法进行回归以检验残差平方的自相关性:rt = c + µt。对残差进行ARCH-LM检验,以进一步确定回归模型的残差序列是否具有ARCH效应,检验结果见表 3。表 3的ARCH-LM检验表明:F统计量为60.332,对应的P值为0.000,说明拒绝残差项不相关的原假设,表明收益率序列的残差项确实存在相关性,存在显著的ARCH效应。因此,可以用GARCH模型来拟合收益率序列。
| 表3 残差ARCH−LM检验 |
金融序列随着时间变化往往表现出显著的波动聚集特征,序列波动率呈现出典型的尖峰厚尾特征,而且从股票序列的杠杆效应可以看出,好消息和坏消息对股市波动的影响不是对称的。GARCH簇模型能够很好地解决以上问题[14-16]。
笔者结合收益率波动的初步分析结果,分别构造GARCH簇模型来刻画沪深300指数收益率序列的波动,然后对不同GARCH模型进行比较研究确定最优模型,最后基于最佳模型的条件方差计算得到VaR和CVaR,用以分析和测度股票市场的风险。
2.2.1 GARCH(1, 1)模型模型太过复杂将会产生过拟合现象,一般情况下,GARCH(1, 1)模型足以刻画序列的波动特征。笔者使用GARCH(1, 1)模型对收益率的波动性进行分析,均值方程和方差方程设置如下:
| $ sy{l_t} = {\alpha _0} + {\mu _t} $ | (4) |
| $ \delta _t^2 = {\beta _0} + {\beta _1}\mu _{t - 1}^2 + {\beta _2}\delta _{t - 1}^2 $ | (5) |
基于残差为正态分布、学生 t分布、GED分布的GARCH(1, 1)模型的拟合结果见表 4。
| 表4 GARCH(1, 1)估计结果 |
由表 4中GARCH(1, 1)模型估计结果可知,基于残差为正态分布、学生t分布、GED分布的GARCH模型来说,β1+β2均小于1,说明波动序列的条件方差序列是稳定的;而且β1+β2均非常接近1,说明市场对外部冲击的反应函数是以一个比较慢的速度在递减,意味着外部冲击对序列波动的影响效应具有持久性和长记忆特性。
综合看来,三种分布条件下的GARCH模型效果差别较小,这说明收益率序列虽然不服从正态分布,但是只要方程设定无误,正态分布下的GARCH同样适用刻画收益率序列的波动性。
笔者以学生t分布下的GARCH(1, 1)进行说明。均值方程为:
| $ sy{l_t} = 3.08 \times {10^{ - 4}} + {\mu _t} $ | (6) |
条件方差方程为:
| $ \delta _t^2 = 1.42 \times {10^{ - 6}} + 0.0598\mu _{t - 1}^2 + 0.9381\delta _{t - 1}^2 $ | (7) |
从均值方程可以看出,沪深300指数收益率的条件均值为0.0308%,说明沪深300指数平均看来具有正向收益,具有一定的投资价值。β1+β2=0.997 9非常接近1,说明条件方差的冲击对收益率序列的影响具有持久性,GARCH(1, 1)过程平稳,因此对收益率序列的科学预测可以在未来波动逐步衰减的条件下实现。
接下来检验GARCH(1, 1)是否消除了残差的ARCH效应。对模型的残差进行ARCH-LM检验,检验结果见表 5。由表 5可知,F检验统计量为1.140 3,检验P值为0.285 6,大于显著水平0.05,说明GARCH(1, 1)模型的残差序列已经不再具有ARCH效应,模型是有效的,可以准确刻画收益率序列的波动性。
| 表5 GARCH(1, 1)的残差ARCH−LM检验 |
GARCH−M模型又叫均值GARCH模型。高收益总是伴随高风险,金融模型中一般假设收益与风险有关,基于这样的思想,把资产收益率的条件方差加入均值方程中,GARCH(1, 1)−M模型的设定如下:
| $ sy{l_t} = {\alpha _0} + {\alpha _1}{\delta _{t - 1}} + {\mu _t} $ | (8) |
| $ \delta _t^2 = {\beta _0} + {\beta _1}\mu _{t - 1}^2 + {\beta _2}\delta _{t - 1}^2 $ | (9) |
如果α1大于0而且显著,那么说明由条件方差增大引起的风险增加会导致平均收益率增加,因此α1一般解释为风险报酬,用于衡量由风险带来的收益。
基于残差为正态分布、学生t分布、GED分布的GARCH(1, 1)−M模型的拟合结果见表 6。
| 表6 GARCH(1, 1)−M估计结果 |
由表 6中GARCH(1, 1)−M模型估计结果可知,残差为正态分布的估计结果表明均值方程的回归系数均不显著,证明残差为正态分布的假设条件不适用GARCH(1, 1)−M模型。在残差为学生t分布、GED分布的假设条件下,均值方程和条件方差方程的回归系数均显著,说明残差为学生t分布、GED分布的假设条件更适合沪深300指数收益率序列。风险报酬系数分别为0.103和0.117时,均处于5%的显著水平之下,说明更高的收益回报由较高的系统风险产生。这也证实了大多数市场参与者是风险规避类型,在承担高风险的同时要求更高的回报,所以,他们会要求对风险敞口进行补偿。
2.2.3 EGARCH(1, 1)模型经典的GARCH模型是存在一定缺陷的,其中假设条件之一是正向冲击和负向冲击对序列波动的影响是相同的,负向冲击对收益率序列的影响时常要高于正向冲击带来的影响,即杠杆效应往往存在于股票市场,是一种非对称表现。常用的描述杠杆效应的模型之一就是EGARCH模型,它通过添加均值残差与条件标准差的比值项来测度正负冲击对股票市场造成的非对称影响。EGARCH(1, 1)模型条件方差设定如下:
| $ \log \delta _t^2 = {\beta _0} + {\beta _1}\log \delta _{t - 1}^2 + {\beta _2}\left| {\frac{{{\mu _{t - 1}}}}{{{\delta _{t - 1}}}}} \right| + {\beta _3}\frac{{{\mu _{t - 1}}}}{{{\delta _{t - 1}}}} $ | (10) |
基于残差为正态分布、学生t分布、GED分布的EGARCH(1, 1)模型的拟合结果见表 7。
| 表7 EGARCH(1, 1)估计结果 |
由表 7中EGARCH(1, 1)模型估计结果可知,在残差为正态分布、学生t分布、GED分布的假设条件下,条件方差方程的回归系数均显著,而且均显著大于0且均显著小于0,表明沪深300指数收益率波动的确存在杠杆效应。以残差正态分布结果为例,负向冲击对条件方差的影响系数为:−0.137 3 − 0.011 9 = −0.149 2,而正向冲击对条件方差的影响系数为0.137 3−0.011 9=0.125 4,表明收益率序列存在负向杠杆效应。相对于利好消息,利空消息的冲击对于收益率序列的影响更大,意味着当利空消息出现时,投资者对未来持悲观态度,会出现恐慌性抛售。
2.2.4 TGARCH(1, 1)模型TGARCH(1, 1)模型条件方差设定如下:
| $ \delta _t^2 = {\beta _0} + {\beta _1}\mu _{t - 1}^2 + {\beta _2}\mu _{t - 1}^2{d_{t - 1}} + {\beta _3}\delta _{t - 1}^2 $ | (11) |
其中dt−1是虚拟变量,当µt<0时,该虚拟变量为1,否则虚拟变量为0。所以,利空消息µt < 0和利好消息 µt > 0对条件方差的影响是不同的。
基于残差为正态分布、学生t 分布、GED分布的TGARCH(1, 1)模型的拟合结果见表 8。
| 表8 TGARCH(1, 1)估计结果 |
由表 8中TGARCH(1, 1)模型估计结果可知,在残差为正态分布、学生t分布、GED分布的假设条件下,条件方差方程的回归系数均显著大于虚拟变量项的回归系数,而且均显著大于0,说明利好消息对条件方差的影响明显不如利空消息对条件方差的影响。以残差正态分布结果为例,利空消息对条件方差的影响系数为0.055 7+0.014 3=0.07,而利好消息对条件方差的影响系数为0.055 7,表明收益率序列存在负向杠杆效应,相对于利好消息,利空消息的冲击对于收益率序列的影响更大。
2.2.5 GARCH模型簇比较赤池信息准则AIC统计量是常用于衡量统计模型拟合好坏的方法之一[17-18]。赤池信息量准则可以权衡所预计模型的复杂度与此模型拟合数据的优良性,它确立在熵的概念基础上。AIC值最小的模型被优先考虑可以有效避免出现过度拟合的情况,而包含最少自由参数且寻找可以最优解释数据的模型的赤池信息准则是个有效的方法。笔者基于AIC统计量来选择最优模型,择优标准为AIC统计量,越小说明模型效果越好。表 9给出了GARCH模型簇的AIC统计量。
| 表9 GARCH模型族的AIC统计量 |
从表 9可以看出,对于同一种模型,残差基于GED分布的模型AIC统计量要小于残差基于学生t分布的模型AIC统计量,而残差基于学生t分布的模型AIC统计量又要小于残差基于正态分布的模型AIC统计量,说明残差基于GED分布的模型拟合效果最好。EGARCH模型的AIC统计量相比其他模型在任何分布下都是最小,说明EGARCH模型效果最好。然而,不同分布下的模型AIC统计量相差非常小,考虑到GARCH模型风险价值计算效率及复杂度,笔者选择用正态分布下的EGARCH(1, 1)模型来深入度量风险价值。
2.3 基于EGARCH模型的VaR和CVaR比较分析基于EGARCH(1, 1)模型正态分布下得到条件方差的估计值,可以计算得到VaR和CVaR。计算公式如下:
| $ VaR = {p_{t - 1}}\left( {{e^{{\delta _r}{Z_\alpha }}} - 1} \right) $ | (12) |
| $ CVaR = \frac{{{p_{t - 1}}{\delta _t}}}{{1 - \alpha }}\int_{ - \infty }^{ - \alpha } q f(q)dq = \frac{{{p_{t - 1}}\left( {{e^{{\delta _t}|{Z_\alpha }}} - 1} \right)}}{{(1 - \alpha )\sqrt {2\pi } {Z_\alpha }}}{e^{\frac{{ - Z_\alpha ^2}}{2}}} $ | (13) |
pt−1表示前一天的收盘价格,δt表示EGARCH(1, 1)模型得到的条件标准差,Zα表示分位数,在95%的置信水平下,Zα=1.644 8;在99%的置信水平下,Zα=2.326 3。基于公式(12)和公式(13)可以计算得到VaR和CVaR值,结果详见表 10。
| 表10 沪深300指数的VaR和CVaR值 |
基于表 10的VaR和CVaR值,表 11给出了VaR和CVaR值的相关描述统计量。从均值水平来看,99%置信水平下的CVaR(114.8)大于99%置信水平下的VaR(100.2),95%置信水平下的CVaR(88.2)大于95%置信水平下的VaR(70.3),说明在相同置信水平下,CVaR值总是要大于VaR值。也就是说,在相同的风险度量方法下,置信水平越大,意味着风险度量值越大。
| 表11 VaR和CVaR值的描述统计量 |
从表 11可以看出,CVaR值的变动比VaR值的变动更加剧烈,而且在每个单位时间内,CVaR值均要大于VaR值,并且验证了描述统计分析中CVaR(99%)>VaR(99%)>CVaR(95%)>VaR(95%)的结论。当VaR值测度风险失效的时候,CVaR值可以更好地测度风险损失,弥补了VaR值的缺陷。
无论CVaR值还是VaR值,它们的变化趋势跟实际损失的变化趋势是相同的。风险值较高的时间段有2007年至2008年以及2014年至2015年。2007年至2008年这个时间段波动剧烈,这个时间段的风险主要受到了全球金融危机的影响。2009年之后,风险度量值开始逐渐趋向于平稳,直到2014年末至2015年初的这个时间段内,风险度量值又开始急剧上升。
3 结语笔者通过对沪深300指数3 788个交易日的收盘价进行整理分析,得到对数收益率序列的描述统计量和分布特征,研究结果表明:收益率序列并不服从正态分布,呈现典型的尖峰厚尾特征,这一结果符合金融市场资产分布的总体特征。对收益率序列进行ARCH效应检验,结果表明收益率序列具有显著的ARCH效应,即序列在一定时间段内波动非常大,在另一个时间段内波动非常小,呈现典型的波动聚集效应。
同时,在对收益率序列进行GARCH模型拟合的时候,笔者基于正态分布、学生t分布、广义误差分布GED分别用GARCH(1, 1)、GARCH(1, 1)−M、EGARCH(1, 1)、TGARCH(1, 1)进行拟合,GARCH(1, 1)−M模型的风险报酬系数显著大于0,说明较高系统风险将会带来更高的收益回报,投资人在承担高风险的同时要求更高的回报。EGARCH(1, 1)、TGARCH(1, 1)的杠杆系数也验证了股票市场中确实存在杠杆效应,即利空消息带来的冲击要比利好消息带来的冲击更加大。基于AIC信息准则比较了各个不同的模型在不同的分布下的拟合效果,结果表明:残差基于GED分布的模型拟合效果最好,EGARCH相对其他模型拟合效果较好。
最后,笔者基于EGARCH(1, 1)模型得到条件方差的估计值,然后基于GARCH模型的条件方差推算得到在不同置信水平下VaR值与CVaR值。将VaR值与CVaR值进行比较,发现在相同置信水平下,CVaR值总是要大于VaR值;在相同的风险度量方法下,置信水平越大,意味着风险度量值越大。当VaR值测度风险失效的时候,CVaR值可以更好地测度风险损失,弥补了VaR值的缺陷。无论CVaR值还是VaR值,它们的变化趋势跟实际损失的变化趋势是相同的。
| [1] |
Grout P A, Zalewska A. Stock market risk in the financial crisis[J]. International Review of Financial Analysis, 2016, 46(1): 326-345. |
| [2] |
Gagnon M H, Power G J, Toupin D. International stock market cointegration under the risk-neutral measure[J]. International Review of Financial Analysis, 2016, 47(10): 243-255. |
| [3] |
Anggraeni W, Andri K B, Sumaryanto, Mahananto F. The performance of ARIMAX model and vector autoregressive(VAR) model in forecasting strategic commodity price in Indonesia[J]. Procedia Computer Science, 2017, 124(12): 189-196. |
| [4] |
魏伟, 国世平. 中国股市风险预警指标体系分析[J]. 深圳大学学报, 2017(2): 109-116. DOI:10.3969/j.issn.1000-260X.2017.02.016 |
| [5] |
王鹏, 吴金宴. 基于协高阶矩视角的沪港股市风险传染分析[J]. 管理科学学报, 2018(6): 29-42. DOI:10.3969/j.issn.1007-9807.2018.06.003 |
| [6] |
Christou C, Cunado J, Gupta R, Hassapis C. Economic policy uncertainty and stock market returns in PacificRim countries:evidence based on a Bayesian panel VAR model[J]. Journal of Multinational Financial Manage-ment, 2017, 40(6): 92-102. |
| [7] |
Chen P, Semmler W. Financial stress, regime switching and spillover effects:evidence from a multi-regime global VAR model[J]. Journal of Economic Dynamics and Control, 2018, 91(6): 318-348. |
| [8] |
Mulvey J M, Erkan H G. Applying CVaR for decentralized risk management of financial companies[J]. Journal of Banking & Finance, 2006, 30(2): 627-644. |
| [9] |
张协奎, 代晓玲. 我国高房价与金融风险的关系分析——基于VAR模型[J]. 价格月刊, 2018(7): 7-14. |
| [10] |
阮向前. 美元国际化与美国金融国际化及其对我国的启示——基于VAR模型的实证分析[J]. 区域金融研究, 2019(1): 31-35. DOI:10.3969/j.issn.1674-5477.2019.01.006 |
| [11] |
Yao F G, Wen H M, Luan J Q. CVaR measurement and operational risk management in commercial banks according to the peak value method of extreme value theory[J]. Mathematical and Computer Modelling, 2013, 58(1-2): 15-27. DOI:10.1016/j.mcm.2012.07.013 |
| [12] |
Balbás A, Balbás B, Balbás R. VaR as the CVaR sensitivity:applications in risk optimization[J]. Journal of Computational and Applied Mathematics, 2017, 309(1): 175-185. |
| [13] |
吕东杰. 基于GARCH-CVAR模型对投资基金风险测度的理论分析与实证研究[J]. 现代经济信息, 2018(18): 291-292. |
| [14] |
Takaishi T. Rational GARCH model:an empirical test for stock returns[J]. Physica A:Statistical Mechanics and its Applications, 2017, 473(5): 451-460. |
| [15] |
Song J, Kang J. Parameter change tests for ARMAGARCH models[J]. Computational Statistics & Data Analysis, 2018, 121(5): 41-56. |
| [16] |
季喆蕴. 基于GARCH模型的中国沪市周内效应的实证分析[J]. 经贸实践, 2018(13): 28-29. |
| [17] |
杨贵军, 孟杰, 王双喜. 基于赤池信息准则的分类回归决策树剪枝算法[J]. 计算机应用, 2014, 34(S2): 147-150. |
| [18] |
孙建彬, 常雷雷, 谭跃进, 姜江, 周志杰. 基于双层模型的置信规则库参数与结构联合优化方法[J]. 系统工程理论与实践, 2018(4): 983-993. |
 2019, Vol. 21
2019, Vol. 21
