2. 中石油西南油气田分公司勘探开发研究院, 四川 成都 610041
2. Research Institute of Exploration and Development, Southwest Oil and Gas Field Branch, PetroChina, Chengdu Sichuan, 610041, China
油田操作成本也称作业成本,它主要是指将地下的原油提升到地面所产生的相关费用,主要包括材料费、燃料费、动力费、人工费以及相关的管理费等[1]。操作成本在油田生产成本中占据了相当大的比例,尤其是对于已进入高含水开发阶段的水驱油田,开发难度不断加大,产油量逐年下降而操作成本却逐年上升。在产量递减和高含水率的情况下,合理有效地预测油田操作成本,对油田企业控制生产成本、提高经济效益、实现可持续发展有着重要的意义。
国内外诸多学者运用各种定性或定量的方法对油田操作成本的影响因素进行了分析。国内李斌、吴晨洪运用灰色关联分析方法对油气生产成本进行分析,发现分项成本与操作费用密切相关的分别是油气处理费、材料费、动力费、测井试井费、燃料费、工资福利费[2];李丰等运用主成分方法分析操作成本后发现,含水率、居民消费指数、注水量、产液量对操作成本影响很大[3]。国外学者对操作成本影响因素的研究侧重于通过建立模型来分析成本形成的原因。Balch认为,油气生产的成本越来越高,一方面原因是由于物价的上涨导致材料费用、燃料费用和外包作业费用的增加;另一方面是由于油田开发后期大多采用注水开采方式,注水、液体提升以及油气处理等环节电力消耗都较大,电力成本的上升是导致油田生产成本增高的主要原因[4];Robert和Stiles也指出,电力成本是影响油气生产成本最大的一项因素,油气提升、油气处理、气体压缩、脱水等生产环节都会增加电力消耗[5]。
综上所述,油田操作成本受多种因素的影响,比如油藏地质属性、油田的开发阶段和经营管理水平等,因此,对油田操作成本进行预测需要考虑多个影响因素。目前已有多种方法和技术被应用于油田成本的预测中,如:灰色关联预测法、回归分析法、组合预测法、神经网络预测法等。回归分析是应用最为广泛的预测方法之一,但在多元线性回归分析中,自变量之间往往存在多重相关性。在油田操作成本实际预测中,样本数据往往是有限的,在这些情况下建立的预测模型是不稳定的,预测结果误差较大[6-8]。
偏最小二乘回归能很好地解决这些实际问题。偏最小二乘方法是Wold和Albano等在1983年首次提出,当时是用于解决化学样本分析中存在的变量多重相关性以及解释变量多于样本点等实际问题[9]。王惠文是最早将该方法引入我国的学者之一。他将该方法应用于中国部分沿海城市及内陆城市的经济发展比较分析中,建立了多因变量对多自变量的偏最小二乘回归模型,以便找出影响两类城市在经济发展中的动力因素[10]。由于其解决了普通多元回归方法无法解决的难题,该方法目前已经在诸多领域被广泛应用。基于此,笔者将该方法用于油田操作成本的预测建模中,并通过油田实际数据对建立的预测模型进行分析,检验该方法应用于操作成本预测的可靠性。
1 偏最小二乘回归的基本原理 1.1 偏最小二乘回归的思路记因变量集合为Y = (y1,y2,…,yq),yj∈Rn,自变量集合为X = (x1x2…xp),xj∈Rn。偏最小二乘回归方法分别在X与Y中提取出成分t1和u1,t1是x1,x2,…,xp的线性组合,u1是y1,y2,…,yq的线性组合。提取的这两个成分应满足两个要求:一是t1和u1应最大程度地携带其各自数据表中的变异信息;二是t1和u1的相关程度最大。
在提取第一个成分t1和u1后,分别实施X对t1的回归和Y对t1的回归,如果回归方程达到满意精度,则终止计算;否则,用X被t1解释后的残余信息和Y被t1解释后的残余信息再度进行成分提取。如此反复,直到达到满意的精度。若最终对X共提取了m个成分t1,t2,…,tm,则实施yk (k = 1,2,…,q)对t1,t2,…,tm的回归分析,最后还原成yk关于原变量x1,x2,…,xp的回归方程。
1.2 偏最小二乘回归的算法首先将X和Y做标准化处理,用E0 = (E01,E02,…,E0p)n*p表示X标准化处理后的数据矩阵,F0表示Y经标准化处理后的变量。
第一步,从E0中提取第一个成分t1,t1 = E0w1,其中w1是E0的第一个轴,即||w1|| = 1。从F0中提取第一个成分u1,u1 = F0c1,且||c1|| = 1。由于F0(F0∈Rn)只是一个变量,所以c1是个标量,即c1=1,即有:u1=F0
根据前述需满足的两个要求以及主成分分析和典型相关分析原理,综合起来即是求t1和u1的协方差达到最大,可以得到下列优化问题:
| $ \begin{array}{l} \max \left\langle {{E_0}{w_1},{F_0}{c_1}} \right\rangle \\ {\rm{s}}{\rm{.t}}\left\{ {\begin{array}{*{20}{c}} {{w_1}^{\rm{T}}{w_1} = 1}\\ {{c_1}^{\rm{T}}{c_1} = 1} \end{array}} \right. \end{array} $ | (1) |
推导可得
| $ \left\{ {\begin{array}{*{20}{c}} {{E_0}^{\rm{T}}{F_0}{F_0}^{\rm{T}}{E_0}{w_1} = {\theta _1}^2{w_1}}\\ {{F_0}^{\rm{T}}{E_0}{E_0}^{\rm{T}}{F_0}{c_1} = {\theta _1}^2{c_1}} \end{array}} \right. $ | (2) |
式中,θ1是目标函数值,w1是矩阵E0TF0F0TE0最大特征值的单位特征向量,对应的特征值为θ12。c1是对应于矩阵F0TE0E0TF0最大特征值θ12的单位特征向量。则
| $ {w_1} = \frac{{{E_0}^{\rm{T}}{F_0}}}{{\left\| {{E_0}^{\rm{T}}{F_0}} \right\|}} = \frac{1}{{\sqrt {\sum\nolimits_{j = 1}^p {{r^2}\left( {{x_j},y} \right)} } }}\left( {\begin{array}{*{20}{c}} {r\left( {{x_1},y} \right)}\\ {r\left( {{x_2},y} \right)}\\ \cdots \\ {r\left( {{x_p},y} \right)} \end{array}} \right) $ | (3) |
| $ \begin{array}{l} {t_1} = {E_0}{w_1} = \frac{1}{{\sqrt {\sum\nolimits_{j = 1}^p {{r^2}\left( {{x_j},y} \right)} } }}\left[ {r\left( {{x_1},y} \right){E_{01}} + } \right.\\ \left. {r\left( {{x_2},y} \right){E_{02}} + \cdots + r\left( {{x_p},y} \right){E_{0p}}} \right] \end{array} $ | (4) |
式中:r(xj,y)是xj与y的相关系数。分别求E0、F0在t1上的回归,即
| $ \left\{ {\begin{array}{*{20}{c}} {{E_0} = {t_1}{p_1}^{\rm{T}} + {E_1}}\\ {{F_0} = {t_1}{r_1} + {F_1}} \end{array}} \right. $ | (5) |
式中:P1、r1是回归系数,
然后进行偏最小二乘回归的第二步,即:分别以E1、F1取代E0、F0,重复第一步得到w2、t2,分别求E1、F1在t2上的回归。依此类推得到m个成分t1,t2,…,tm,可以得到F0关于th的偏最小二乘回归模型:
| $ {F_0} = {r_1}{t_1} + {r_2}{t_2} + \cdots + {r_m}{t_m} + {F_m} $ | (6) |
因为th均为E0的线性组合,所以
| $ {F_0} = {r_1}{E_0}{w_1}^ * + {r_2}{E_0}{w_2}^ * + \cdots + {r_m}{E_0}{w_m}^ * + {F_m} $ | (7) |
式中,
| $ {{\hat y}^ * } = {a_1}{x_1}^ * + {a_2}{x_2}^ * + \cdots + {a_p}{x_p}^ * $ | (8) |
最后按照标准化的逆过程还原成因变量y关于x1,x2,…,xp的回归方程。
1.3 交叉有效性记yi为原始数据,t1,t2,…,tm是提取的m个成分,
| $ {S_{S{\rm{S}},h}} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_{hi}}} \right)}^2}} $ | (9) |
| $ {S_{{\rm{PRE}}S{\rm{S}},h}} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_{h\left( { - {\rm{i}}} \right)}}} \right)}^2}} $ | (10) |
| $ {Q_h}^2 = 1 - \frac{{{S_{{\rm{PRE}}S{\rm{S}},h}}}}{{{S_{S{\rm{S}},h}}}} $ | (11) |
当Qh2 ≥ 0:097 5时,增加新的成分th,对所建模型的预测能力有明显的改善,否则增加的新成分没有显著意义。
2 油田操作成本偏最小二乘回归预测模型的建立在求建油田操作成本偏最小二乘回归预测模型时,笔者只将油田操作成本作为因变量,因变量只有一个,即q=1,因此该模型是一个单因变量的偏最小二乘回归模型。
2.1 自变量的选取李丰等在对高含水水驱油田操作成本预测分析时,针对水驱油田的特点,从生产控制、开发阶段和宏观经济形势三个方面综合考虑,选取了产油量、产液量、注水量、含水率、开井数、工作量、油价、价格指数和居民消费指数等9项操作成本影响因素作为主要影响指标[3]。李萍等从油田开发生产和油田财务的角度,选取了措施增油比重、开井率、含水率、注采比、平均单井产油量、自然递减率、可采储量采出程度、平均泵挂深度、平均注水油压、吨油单井集油线占比、吨油资产占比、资产新旧系数、吨油拉油费等13个影响因素作为主要影响指标,对操作成本和主要指标进行多元线性回归[11]。笔者在选取自变量指标时,实际上是基于两点:一是以上述研究选取的主要指标作为参考,并结合DX油田的实际情况来确定自变量指标;二是根据DX油田数据,充分考虑自变量指标的可量化和可测度性质,因为难以量化和测度的指标没有统计数据支持,纳入研究分析框架将影响预测模型的可靠性。基于以上两点,针对特高含水水驱油田成本变化规律的自变量主控指标,笔者选取了7个自变量:产液量(x1)、产油量(x2)、注水量(x3)、含水率(x4)、措施工作量(x5)、工业品购进价格指数(x6)和电力价格(x7)。
2.2 原始数据的来源DX油田是国内最早进入以水驱为主的特高含水开发油田之一,以DX油田2010年至2016年的操作成本:产液量、产油量、注水量、含水率、措施工作量以及对应年份的工业品购进价格指数和电力价格等实际数据为例(表 1),运用前述方法建立该油田的操作成本预测模型。
| 表1 DX油田操作成本及相关数据 |
通过计算,得到7个自变量和因变量之间的相关系数,结果如表 2。从表 2中可以看出,自变量之间存在高度的多重相关性。
| 表2 自变量及因变量的相关系数 |
应用SIMCA−P软件建立偏最小二乘回归模型。首先计算对因变量y的交叉有效性,Qh2表示成分th的交叉有效性,Qh2(cum)表示使用m个提取成分t1,t2,…,tm建模的累计交叉有效性。从表 3可以看出,提取到第3个成分时,Q32=−0.414 4,小于0.097 5,且Q22(cum)=0.997 0, 已经达到满意的精度,故提取2个偏最小二乘成分即可。
| 表3 对因变量y的交叉有效性 |
表 4是wh*(h=1, 2)的取值。ph(h=1, 2)是在利用Eh−1对th进行回归时得到的回归系数,其取值如表 5。
| 表4 wh*的取值 |
| 表5 回归系数ph |
由上述偏最小二乘算法的推导过程可知,F0可以表示为提取的成分th的回归方程,因此,最终得年到标准化变量F0与E0j(j=1,2,3,4,5,6,7)的回归方程:
| $ \begin{array}{l} {F_0} = 0.229247{E_{01}} - 0.187106{E_{02}} + 0.11418{E_{03}} + \\ 0.178044{E_{04}} + 0.0073003{E_{05}} + 0.180363{E_{06}} + \\ 0.159716{E_{07}} \end{array} $ | (12) |
将标准化变量F0与E0j(j=1,2,3,4,5,6,7)分别还原为原始变量,最终得到的预测模型为:
| $ \begin{array}{l} y = - 337857 + 79.1988{x_1} - 245.577{x_2} + \\ 23.1102{x_3} + 2970.71{x_4} + 2.08878{x_5} + 254.999{x_6} + \\ 29590.1{x_7} \end{array} $ | (13) |
图 1能够直观反映回归模型拟合的效果,显示了提取的2个主成分对输出变量y的累积解释能力(R2(cum))和累计交叉有效性(Q2(cum))。从图 1中可以看出,2个主成分的累计解释能力几乎达到了1(实际R2(cum)=0.999 02),已经达到非常高的精度,说明上面建立的预测模型拟合程度非常好。
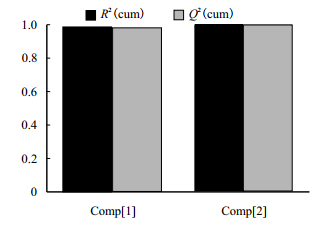 |
| 图1 模型拟合结果图 |
用建立的预测模型(公式13)对DX油田2010年至2016年的操作成本进行预测,将实际数据代入公式13计算出预测值与实际值的相对误差,得到的预测值和相对误差结果见表 6。表 6表明,预测值的平均相对误差为0.003 162,且所有年份的预测值相对误差都很小,证明预测精度检验的结果十分乐观,建立的预测模型具有很强的可操作性。
| 表6 DX油田操作成本预测精度检验表 |
在偏最小二乘回归中,可以通过th和uh的线性关系来判断自变量与因变量之间的关系。从图 2可以看出,DX油田的操作成本与解释变量间存在明显的线性关系,说明建立操作成本与解释变量的线性回归模型是合理的。
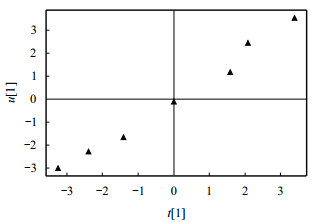 |
| 图2 t[1]/u[1]平面图 |
自变量在解释因变量时的重要性可以通过VIPj值来反应。表 7是各个自变量的VIPj值,其中x1、x2、x4、x7四个变量的重要性指标值均超过1,且差别不大,其他3个变量都低于1,说明产液量、产油量、含水率、电力价格4个因素对油田操作成本都有着较强的影响作用,是引起操作成本变动的主要因素。
| 表7 VIPj值表 |
图 3是在标准化数据下的回归方程对应自变量的回归系数直方图,它直观地反映了各自变量指标对DX油田操作成本的边际贡献。从图 3中可以看出,产液量、注水量、含水率、措施工作量以及工业品购进价格指数和电力价格对DX油田操作成本起正向作用。也就是说,这几个因素的增长会导致DX油田操作成本的增长,其中措施工作量的回归系数几乎为0,对操作成本的增长影响不大。产油量与操作成本呈负相关关系。这里需要说明的是,并非增加产油量就能降低操作成本,而是因为DX油田早已进入特高含水开发期,产油量在逐年下降。为保持年产油量在一定的水平,需要采取有效措施,如增大注水量等,这势必会导致操作成本的增加,因此产油量和操作成本才呈现出负相关关系。
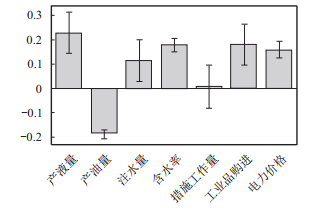 |
| 图3 回归系数直方图 |
通过对模型的分析评价,可见采用偏最小二乘回归方法来进行油田操作成本的预测建模,能够很好地解决自变量之间的多重共线性问题,建立的模型具备较强的预测能力。
4 结语笔者基于DX油田2010年至2016年的操作成本、产液量、产油量、注水量、含水率、措施工作量以及对应年份的工业品购进价格指数和电力价格等实际数据,建立了偏最小二乘回归预测模型,并对模型进行了检验和评价,得到以下结论:
(1)油田操作成本受到产液量、产油量、注水量、含水率、工业品购进价格指数、电力价格等多种因素的影响,且根据相关性检验可知这些影响因素之间存在着高度的相关性,采用普通多元回归将会遇到严重的多重共线性问题。
(2)通过偏最小二乘回归方法建立的DX油田操作成本预测模型,其解释变量对因变量的解释能力达到了0.999 02,且将实际数据代入预测模型得到的预测值的平均误差仅为0.003 162,预测精度非常高,表明偏最小二乘回归方法能够很好地解决自变量之间的多重相关性问题。因此,采用基于偏最小二乘回归来预测油田操作成本不失为一种好的方法。
| [1] |
张继成, 梁文福, 赵玲, 宋考平, 甘晓飞. 喇嘛甸油田特高含水期开发形势分析[J]. 东北石油大学学报, 2005, 29(3): 23-25. DOI:10.3969/j.issn.2095-4107.2005.03.008 |
| [2] |
李斌, 吴晨洪, 邵玉明. 油气生产成本的关联分析[J]. 国际石油经济, 2001, 8(6): 37-40. DOI:10.3969/j.issn.1004-7298.2001.06.012 |
| [3] |
李丰, 张晓辉, 曲德斌, 曲海旭. 基于主成分回归模型的水驱油田操作成本预测[J]. 石油天然气学报, 2012, 34(9): 136-139. DOI:10.3969/j.issn.1000-9752.2012.09.030 |
| [4] |
Balch G R. Electricity Cost Reductions in the Oil Field[C]//Permian Basin Oil and Gas Recovery Conference. Midland: Society of Petroleum Engineers, 1990. https://www.onepetro.org/conference-paper/SPE-20102-MS
|
| [5] |
Robert F, Stiles M, Steven Slezak. Strategies for reducing oilfield electric power costs in a deregulated market[J]. SPE Production & Facilities, 2002, 17(3): 171-178. |
| [6] |
王惠文. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999: 200-234.
|
| [7] |
王惠文. 偏最小二乘回归的线性与非线性方法[M]. 北京: 国防工业出版社, 2006: 97-141.
|
| [8] |
吴茜茜, 侯春华, 陈武, 赵小军, 余晓钟. 特高含水水驱油田操作成本组合预测方法研究[J]. 石油化工技术与经济, 2014, 30(6): 5-9. DOI:10.3969/j.issn.1674-1099.2014.06.002 |
| [9] |
Wold S, Albano C, Dunn W J. Pattern regression finding and using regularities in multivariate data[J]. Analysis Applied Science, 1983, 147-188. |
| [10] |
王惠文. 用PLS回归方法对中国沿海与内陆城市经济的比较分析[J]. 数理统计与管理, 1998(5): 10-15. |
| [11] |
李萍, 毛琼, 王新颖, 王旭东, 王晓芸. 基于多元线性回归分析的操作成本预测模型建立与应用[J]. 石油规划设计, 2018, 29(3): 33-37, 52. DOI:10.3969/j.issn.1004-2970.2018.03.010 |
 2019, Vol. 21
2019, Vol. 21

