2. 福建农林大学经济学院, 福建 福州 350002
2. College of Economics, Fujian Agriculture and Forestry University, Fuzhou Fujian, 350002, China
在实际生活中,交易费用、税收、红利等一些无足轻重的摩擦往往会在证券交易市场中产生,而就大众而言,以上提到的这些摩擦常常会被他们忽视,这个忽视在交易量相当大的情况下是合乎常理的,然而在交易量很小的情况下,这些摩擦对投资者的投资决策影响是不能忽略的。一些学者深入探究了交易费用的相关问题,如Arnott及Wagner[1]研究表明,对交易费用的忽视将会使投资组合无效;Akian等[2]讨论了存在V型交易费用的投资组合优化及求解问题;胡国政、李楚霖[3]拓广(展)了Markowitz均值方差模型,研究了考虑交易费用的投资组合问题;吴孟铎、荣喜民、李践[4]讨论了交易成本对证券投资组合边界的影响;刘明明、高岩[5-6]讨论了V型交易费用的最优投资组合选择问题;市场的主要影响因素无疑是离不开交易成本,这是埃德温等人的观点[7],据观测,究竟多大的价格偏差会使投资者的投资策略改变是与交易成本息息相关的,其对最优投资组合的影响更是显著。因此,很有必要把交易费用放在投资组合模型中加以考虑。目前,理论上的交易成本主要分为三种类型:线性交易成本,V型交易成本和非线性交易成本。本研究考虑成比例交易费用,并且结合我国股市,拓展均值CVaR模型,建立成比例交易费用的均值CVaR单期投资组合优化模型,并进行实证分析。
1 CVaR的简单描述条件风险值(Conditional Value-at-Risk,CVaR)产生的基础是风险价值(VaR),它比VaR更加全面与完善。CVaR这个全新的风险度量手段是Rockafeller为了改进VaR的缺点于1999年提出的。它的基本含义是:在一定的置信水平下,CVaR比VaR的潜在损失价值高。相比VaR,它可以使投资组合的隐性风险更加得以体现。其数学表达为式(1):
| $\begin{align} & CVaR=E\left[ f\left( x,y \right)|f\left( x,y \right)\ge VaR \right] \\ & =VaR+E\left[ f\left( x,y \right)-VaR|f\left( x,y \right)\ge VaR \right] \\ \end{align}$ | (1) |
其中,f(x, y)是在决策向量x下的损失函数;x ∈ X ⊆ Rn(则是可行集)是决策向量,具体指每种资产在投资组合中的头寸或权重;y ∈ Rn是随机向量,指损失产生的不确定性,如资产市场价格或收益率。
具体来讲,如在置信水平为95%的情况下,一投资组合在2008年10月10日当日的VaR值是80万元,CVaR值是100万元,表示有95%的把握,这种资产组合因为市场风险而造成的损失不会超过80万元,而有95%的把握确保这种资产组合因市场风险因子变化而造成的极端隐性损失不超过100万元。
2 成比例交易费用的CVaR单期投资组合模型不管是买进或是卖出股票,投资者在实际投资过程中均要缴纳一定的交易费用,交易费用会对投资者的最后收益产生影响,因此,在进行投资决策时,考虑交易费用是非常必要的。假定交易费用为线性,投资者对n种股票进行买进或者卖出,通过不断调整它们在投资组合中的比例以求解最优投资组合。就第i种股票而言,交易费用为交易金额的ci倍,则如果交易金额越来越大,交易费用也就越高。就现金交易而言,假定c0=0,交易费用函数可表示为(2):
| $C\left( {{x}_{i}} \right)={{c}_{i}}{{q}_{i}}\left| {{x}_{i}}-x_{i}^{0} \right|$ | (2) |
其中,ci为单位股票的交易费率,qi是n种股票的当前价格,xi0是股票组合初始持有量,xi是优化后股票的持有量,qixi表示最优投资组合下各股票的头寸。
假设初始资产全为现金T,那么股票的初始持有量为零,投资者考虑买入多少目标股票,在一定置信度β下,获得期望收益率R0而风险最小。
由于全部情形的加权以及近似对在CVaR函数中的积分加以表示,所以,对CVaR进行计算的前提条件是取得股票收益这一情形。考虑一个持有时期的n种投资组合最小化问题,对以前相当长的一段时间(m+1天)的相关历史数据加以运用会使m个情景下的收益得以产生。假如持有期限为1天,于是对收益率进行计算时我们对股票接连两个交易日的收盘价格要加以运用,换句话说,pj和pj+1,yij对第i种股票在情景j下取得的收益率进行表示,E[yi]对第i种证券的期望收益率进行表示。假定可能产生将来m种情景等一些概率,即πj=m-1,有:
| ${{y}_{ij}}=\left( p_{i}^{j+1}-p_{i}^{j} \right)/p_{i}^{j},i=1,\cdots ,n$ | (3) |
| $E\left[ {{y}_{i}} \right]=\sum\limits_{j=1}^{m}{{{m}^{-1}}{{y}_{ij}}}$ | (4) |
由于组合的损失等于负收益,则情形j下投资组合的损失函数为:
| $f\left( x,{{y}_{j}} \right)=\sum\limits_{i=1}^{n}{{{c}_{i}}{{q}_{i}}{{x}_{i}}-}\sum\limits_{i=1}^{n}{{{y}_{ij}}{{q}_{i}}{{x}_{i}}}$ | (5) |
假如实行投资组合优化要采用CVaR作为风险度量用具,那么辅助函数F(x, α)为凸形,并且呈现出连续可微的情形,采用下面的式子能够近似表达函数F(x, α):
| ${{{\hat{F}}}_{m}}\left( x,\alpha \right)=\alpha +\frac{1}{m\left( 1-\beta \right)}\sum\limits_{j=1}^{m}{{{\left[ f\left( x,{{y}_{j}} \right)-\alpha \right]}^{+}}}$ | (6) |
将其线性化,则
| $\alpha +\frac{1}{m\left( 1-\beta \right)}\sum\limits_{j=1}^{m}{{{z}_{j}}}$ | (7) |
| ${{z}_{j}}\ge f\left( x,y \right)-\alpha ,{{z}_{j}}\ge 0,j=1,\cdots ,m$ | (8) |
资产平衡约束为:
| $\sum\limits_{i=1}^{n}{{{c}_{i}}{{q}_{i}}{{x}_{i}}}+\sum\limits_{i=1}^{n}{{{q}_{i}}{{x}_{i}}}=T$ | (9) |
收益约束为:
| $\sum\limits_{i=1}^{n}{E\left( {{y}_{i}} \right){{q}_{i}}{{x}_{i}}}\ge {{R}_{0}}\sum\limits_{i=1}^{n}{{{q}_{i}}{{x}_{i}}}$ | (10) |
为了分散投资降低风险,假设在第i种股票风险资产上的投资额不能超过总资产的ei倍,即
| ${{q}_{i}}{{x}_{i}}\le {{e}_{i}}\sum\limits_{i=1}^{n}{{{q}_{i}}{{x}_{i}}}$ | (11) |
因此考虑成比例交易费用时,在给定置信度和期望收益率下,使组合风险最小的单期均值CVaR优化模型则是:
| $\begin{gathered} \mathop {\min }\limits_{x,\alpha } + \frac{1}{{m\left( {1 - \beta } \right)}}\sum\limits_{j = 1}^m {{z_j}} \hfill \\ s.t.\left\{ \begin{gathered} {z_j} \geqslant \sum\limits_{i = 1}^n {{c_i}{q_i}{x_i}} - \sum\limits_{i = 1}^n {{y_{ij}}{q_i}{x_i} - \alpha } \;\;\;j = 1, \cdots ,m \hfill \\ {z_j} \geqslant 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1, \cdots ,m \hfill \\ \sum\limits_{i = 1}^n {{c_i}{q_i}{x_i} + } \sum\limits_{i = 1}^n {{q_i}{x_i} = T} \hfill \\ \sum\limits_{i = 1}^n {E\left[ {{y_i}} \right]{q_i}{x_i} \geqslant {R_0}} \sum\limits_{i = 1}^n {{q_i}{x_i}} \hfill \\ {q_i}{x_i} \leqslant {e_i}\sum\limits_{i = 1}^n {{q_i}{x_i}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \cdots ,n \hfill \\ {x_i} \geqslant 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \cdots ,n \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ | (12) |
此模型的求解为带有不等式约束的线性规划问题,可以使用Matlab软件求解该模型,得到最优投资组合x*时,能同时得到对应的最小CVaR和VaR值。对不相同的收益率约束下的最优问题进行求解可以求出资产组合的有效前沿。对于有效前沿上的给定点,不可能产生比给定点稍高的回报但存在较低的风险的点[8-10]。因此,在一定置信水平下,成比例交易费用的均值CVaR模型的有效前沿曲线由最优投资组合x*对应的一些(R*, CVaR(x*))点组成,其中R*是最优投资组合的收益率,CVaR (x*)是最优投资组合的条件风险值。
3 模型实证分析及比较抽取上海证券交易所上市交易的8支股票作为样本,针对这8支样本股票进行分析。样本时间跨度为2013年12月4日至2014年12月11日,选取每支股票的日收盘价。若个股存在某个交易日停牌或其他数据缺失的情况,对缺失数据用前一日的交易数据替代。当对第i种风险资产在情景j下的收益率yij进行计算时要采用历史模拟法的(3)式,在这个地方取i=1, …, 8,j=1, …, 250,且假设投资期初的现金为25万,不考虑税收和红利,不允许买空、卖空。设交易费率ci=0.005,ei=0.25,以2014年12月26日的标的股票收盘价为当前价格,用Matlab软件求解模型(12),计算出在给定置信水平下的不同期望收益率、最优投资组合、有效前沿及VaR和CVaR值。
对于确定的资产组合而言,其均值方差模型只有一个投资组合有效前沿。而均值CVaR模型有无数个投资组合有效前沿,不同置信水平下均有一个有效的投资组合前沿(见图 1)。
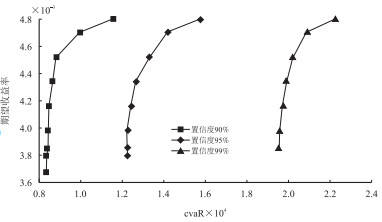 |
| 图1 不同置信水平下的投资组合有效前沿 |
由图 1可以看出,投资组合的有效前沿线随置信水平的变化而移动,并表现出以下特点:
(1)有效前沿和投资组合的可行集随置信水平的持续变大很快地朝右方移动。与之对应的CVaR值在相同的期望收益率下持续变大。例如:当期望收益率R0是0.004 52时,在置信水平是90%的情况下,那么CVaR值则是12 609.76;置信水平为95%时,CVaR值为15 964.35;置信水平为99%时,CVaR值为21 175.34。同时,分别在不同的置信水平,投资组合中每支股的配置也随之发生了比较大的变化,详见表 1。
| 表1 不同置信水平下投资组合资产配置及CVaR值 |
由表 1可得出,不同置信水平下,投资组合有效前沿不同;即便是相同的期望收益率,不同的置信水平投资组合也不一样。因此,对置信水平的合理选择,会对投资者的投资策略产生影响。
(2)不同置信水平下,投资组合有效前沿的最大期望收益相同,为0.004 83,而最小期望收益则随着置信水平的增加而逐渐变大,依次为0.003 62,0.003 72,0.003 78,期望收益率可取值的范围逐渐变小,那么意味着投资者在期望收益率上选择的空间变小。
(3)给定置信水平下,期望收益率R0越高,风险也越大,这符合“高收益、高风险”的投资规律。最优CVaR值越大,投资组合将更多地集中于收益高的部分资产;最优CVaR值呈现出越来越低的数值,投资组合中资产也呈现出越来越不太集中的布局(见表 2),(假设置信水平为95%)。
| 表2 置信水平95%时不同期望收益的投资组合资产配置及CVaR、VaR值 |
由表 2可见,得到最小CVaR值的同时也得到VaR值,并且CVaR值不小于VaR值。表中期望收益率R0=0.004 52时对应的VaR值小于R0=0.004 32对应的VaR,也说明了VaR不是一致性风险度量工具,而CVaR是一致性风险度量工具。
表 3为不考虑交易费和成比例交易费情况下的最优投资组合和CVaR、VaR值,在期望收益率R0是0.004 52的情况下,没有交易费用的CVaR值是14 794.2,与此同时,成比例交易费用的CVaR值变大,其值是15 964.4,结果与考虑交易费用时一致,同时也表明CVaR要优于VaR。
| 表3 不考虑交易费情况下不同收益率的投资组合资产配置及CVaR、VaR值 |
从图 2可以看出,促使投资组合有效前沿向右移动的原因毫无疑问是成比例交易费用的产生,然而CVaR值是变大的,这里指的是同一期望收益率所对应的CVaR值。成比例交易费用和不考虑交易费用的有效前沿对应的期望收益率区间基本没有变化,但是最优投资策略中各股的持有量有明显的差别,不过最优决策下的目标股票都是相同的,可见交易费用对股票的持有量有很大的影响,选择适当的交易费用计量方法对投资者具有指导意义。
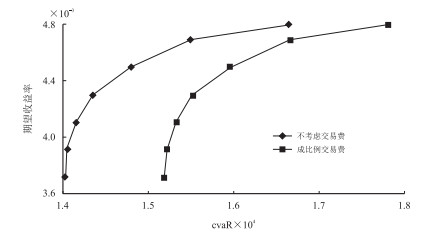 |
| 图2 不考虑交易费和成比例交易费情况下的相关投资组合的有效前沿 |
将函数
对于非光滑函数[t]+,用光滑技术来处理这类非光滑函数,就是要寻找一个带参数的光滑近似函数ρ(t, ε)来逼近原函数。光滑函数ρ(t, ε)是连续可微的,ε > 0充分小,并且当ε → 0时有|t -ρ(t, ε)| → 0。笔者选择常用的连续可导分段二次凸函数P(t, ε)来光滑近似[t]+,为满足一阶光滑性和近似性,P(t, ε)需满足:
| $\frac{d\left( P\left( t,\varepsilon \right) \right)}{dt}{{|}_{t=\varepsilon }}=1\frac{d\left( P\left( t,\varepsilon \right) \right)}{dt}{{|}_{t=\varepsilon }}=0$ | (13) |
| $\begin{gathered} P\left( {t,\varepsilon } \right){|_{t = \varepsilon }} = tP\left( {t,\varepsilon } \right){|_{t = \varepsilon }} = 0 \hfill \\ P\left( {t,\varepsilon } \right) = \left\{ \begin{gathered} t\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > \varepsilon \hfill \\ \frac{{{t^2}}}{{4\varepsilon }} + \frac{1}{2}t + \frac{1}{4}\varepsilon \;\;\;\;\; - \varepsilon \leqslant t \leqslant \varepsilon \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t < - \varepsilon \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ | (14) |
那么
| $\begin{gathered} \tilde F\left( {x,\alpha ,\varepsilon ,{y_j}} \right) = \left\{ \begin{gathered} f\left( {x,{y_j}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f\left( {x,{y_j} > \varepsilon } \right) \hfill \\ \frac{1}{{4\varepsilon }}f{\left( {x,{y_j}} \right)^2} + \frac{1}{2}f\left( {x,{y_j}} \right) + \frac{1}{4}\varepsilon \;\;\; - \varepsilon \leqslant f\left( {x,{y_j}} \right) \leqslant \varepsilon \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f\left( {x,{y_j}} \right) > - \varepsilon \hfill \\ \end{gathered} \right. \hfill \\ f\left( {x,{y_j}} \right) = \sum\limits_{i = 1}^n {{c_i}{q_i}{x_i}} - \sum\limits_{i = 1}^n {{y_{ij}}{q_i}{x_i} - \alpha } \hfill \\ \end{gathered} $ | (15) |
因此考虑成比例交易费用时,在给定置信度β和期望收益率R0下,投资组合风险最小的单期均值CVaR光滑化的非线性规划近似模型为:
| $\begin{gathered} \mathop {\min }\limits_{x,\alpha } + \frac{1}{{m\left( {1 - \beta } \right)}}\sum\limits_{j = 1}^m {\tilde F\left( {x,\alpha ,\varepsilon ,{y_j}} \right)} \hfill \\ s.t.\left\{ \begin{gathered} \sum\limits_{i = 1}^n {{c_i}{q_i}{x_i} + } \sum\limits_{i = 1}^n {{q_i}{x_i}} = T \hfill \\ \sum\limits_{i = 1}^n {E\left[ {{y_i}} \right]{q_i}{x_i} \geqslant {R_0}\sum\limits_{i = 1}^n {{q_i}{x_i}} } \hfill \\ {q_i}{x_i} \leqslant {e_i}\sum\limits_{i = 1}^n {{q_i}{x_i}} \;\;\;\;i = 1, \cdots ,n \hfill \\ {x_i} > 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \cdots ,n \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ | (16) |
对于平滑技术,连续可导近似函数
同样选取前文的实例进行数值实验。取ε=0.01,考虑成比例交易费,用Matlab求解光滑模型(13),得到置信水平95%下不同期望收益率对应的最优投资组合,CVaR、VaR值如表 4所示。
对比表 2和表 4可以发现,期望收益率R0=0.004 52或0.004 83时光滑模型的CVaR与线性模型的CVaR值很接近,其它时候光滑模型与线性模型的CVaR值有很小的偏差,究其原因是光滑函数在近似
| 表4 置信水平95%情况下不同期望收益率的光滑模型投资组合资产配置及CVaR、VaR值 |
根据证券交易的实际需要,本研究考虑成比例交易费用,建立了新的均值CVaR单期投资组合模型。新模型以股票持有量为决策变量,比以股票权重为决策变量的模型求解的最优投资策略和CVaR值更加直观。交易费用会影响资产的损失和收益,因此新模型的目标函数、资本平衡约束、收益约束相对于均值CVaR模型(12)有所调整,模型更加完善合理。
本研究对新模型实行综合的实例解析,通过每种约束对最优投资组合以及有效前沿的影响分析可以看出,随着置信度90%,95%,99%的不断增大,期望收益率可选择的范围变小,CVaR值增大,投资组合的有效前沿向右移动;同一置信水平下,期望收益率越高,对应的CVaR值越高,验证了“高收益伴随高风险”的投资理论。在实际的投资决策中,投资者要根据自身的情况选择合理的置信度;成比例交易费用与不考虑交易费用相比,期望收益率可选择区间基本没有变化,相同置信水平和期望收益率下的CVaR值较大,有效前沿向右移动,最优投资策略有明显的不同。因此,考虑成比例交易费用对投资者合理决策、规避风险有着重要的意义。。
对于Rockafellar辅助函数中的非光滑函数[f(x, yj)-α]+,流行的方法是引入虚拟变量将其线性化,把模型转化成线性规划,新模型也采用了此种方法求解。不过这种转化增加了变量和约束,对于大规模情景模拟,增加的约束条件相当复杂,线性规划的计算成本较高。因此笔者还考虑了引入一种光滑函数逼近此类非光滑函数,把模型转化成光滑化的非线性规划近似模型。实证模拟说明了处理大规模情景模拟的投资组合问题时,光滑模型的收敛性优于线性模型。虽然光滑模型的结果存在某些误差,但它同样能给投资者一定的参考信息。光滑模型的近似程度取决于参数ε的选取,因此如何合理选择参数使光滑后的问题更加接近原问题将是未来研究的新方向。
| [1] | Arnott R D, Wagner W H. Asset pricing and the bidask spread[J]. Journal of Financial Economics, 1986 (17) : 223 –249. |
| [2] | Akian M J, Menaldi L, Sulem A. Multi-asset portfolio selection problem with transaction cost[J]. Mathematics and Computers in Simulation, 1995 (38) : 163 –172. |
| [3] | 胡国政, 李楚霖. 考虑交易费用的证券组合投资的研究[J]. 预测, 1998, 17 (5) : 66 –67. |
| [4] | 吴孟铎, 荣喜民, 李践. 有交易成本的组合证券投资[J]. 天津大学学报, 2002, 35 (2) : 196 –198. |
| [5] | 刘明明, 高岩. 摩擦市场中允许卖空的最优投资组合选择[J]. 中国管理科学, 2006, 14 (5) : 23 –27. |
| [6] | 刘明明, 高岩. 摩擦市场中最优证券组合选择的极大极小法[J]. 数学的实践与认识, 2008, 38 (20) : 16 –23. |
| [7] | Mekay R, Keefer T E. VaR is a dangerous technique[J]. Corporate Financial Searching for System Integration Supplement, 1996, 19 (5) : 3035 . |
| [8] | Siddarth A, Thomas F. C, Yuying Li. Minizing CVaR and VaR for Portfolio of Derivatives[J]. The International Conference on Modeling, Optimization and Risk Management in Finance, Gainesville, 2003 : 352361 . |
| [9] | 刘小茂, 李楚霖. 风险资产的均值-CVaR有效前沿(I)[J]. 管理工程学报, 2003, 17 (1) : 29 –32. |
| [10] | 刘小茂, 李楚霖. 风险资产的均值-CVaR有效前沿(II)[J]. 管理工程学报, 2005, 19 (1) : 1 –5. |
 2017, Vol. 19
2017, Vol. 19

