自2003 年英国政府发表了题为Our Energy Future,Creating a Low Carbon Economy的能源白皮书,首次提出低碳经济的概念后,到2012 年10 月《中国的能源政策(2012)》白皮书的发表,“全球气候变暖、减少温室气体排放”的问题已引起国内外广泛关注。在联合国气候峰会与哥本哈根气候大会上,各国就此进行了激烈的博弈,力求在自身利益最大化的情况下建立高效率的节能减排机制,实现低耗能、低排放、低污染的低碳经济。中国政府在恪守“共同但有区别的责任”下,提出2020 年碳排放强度相比“十一五”时期下降40%~45% 的减排目标,并纳入“十二五”规划,写进“十八大”报告,作为接下来很长一段时间内升级经济结构、转变经济发展方式的衡量指标之一。福建省作为引领海峡西岸经济区跨越式发展的重要地区,有必要在转型的同时加大投入实施碳减排和建设低碳经济,争取完成节能减排目标,实现可持续发展。有关碳排放影响因素的研究也越来越多,归纳起来主要可划分为以下两类:
一是从研究方法上看,主要集中于指数分解法。Wang 通过对数平均迪氏指数分解法分解了20世纪后半期中国的CO2 排放,发现能源强度是减少碳排放的主要因素,经济增长则是促进碳排放的重要驱动力[1];徐国泉等定量分析了1995-2004 年间能源结构、效率和经济发展等因素的变化对中国人均碳排放的影响[2];朱勤等应用LMDI 分解法对能源消费碳排放进行因素分解,并探讨了各因素的影响与作用[3];唐建荣等运用因素叠加法对碳排放的影响因素进行了量化分析[4]。
二是从研究区域上看,主要以全国为例或集中于某些产煤、高排区域。雷厉等计量了1995-2008年间中国大部分省市的CO2 排放量,在此基础上对其区域间的差异进行了分析[5];张纪录对15 年来中部地区碳排放水平进行了测算,并对其作对数平均迪氏指数分析[6];郝丽等对陕西省1980-2010年间的碳排放进行阶段划分,并用LMDI 法分析了各阶段的主要影响因素[7],等等。随着研究的拓展和深入,在经济合作与发展组织(OECD)首次提出脱钩概念以分析环境污染与经济发展之间的关系后[8],越来越多的学者也将脱钩指标运用于研究碳减排中。国外学者Tapio 最先将脱钩弹性指标运用于欧洲交通业的经济增长、运输量与碳排放之间关系的研究[9];国内学者李忠民等介绍、运用了OECD脱钩指标并评价、修正了Tapio 脱钩指标,以陕西省为例进行分析,并对中、东、西部的碳排放与经济增长之间的脱钩关系进行了测度分析[10-12];刘怡君等通过Tapio 脱钩弹性指标研究了不同的城市经济发展与能源消耗的关系[13];王云等通过LMDI 法定义CO2 脱钩弹性指标和努力指标,以此构建了低碳经济脱钩量化分解模型,并以山西为例进行了分析[14-15];吴文洁等将脱钩理论与EKC 理论结合起来,对陕西省1995-2009 年间的碳排放与经济增长关系进行脱钩分析,并预测了陕西省以后碳排放量的变动趋势[16],等。
目前对碳排放影响因素研究的不足之处主要集中于碳排放影响因素的指数分解方法分析,或主要以全国层面或产煤、高排省份为研究区域或对象,缺少对研究方法的突破及研究区域上的扩展。而对于碳排放脱钩的研究则较先进,从脱钩指标的提出、运用,再到引入国内学界,并与LMDI 分解法的结合,研究方法上与学界已有方法的结合越来越紧密。
本文在运用以往学者提出的Tapio 脱钩弹性指标的基础上,创新性地引入扩展的Kaya 恒等式来对碳排放的影响因素进行分解,构建Tapio 脱钩弹性分解模型,并以福建省为例,分析其自1990 年以来的碳排放脱钩情况,并以此作情景预测。
1 研究模型与实证分析 1.1 碳排放因素分解模型1990 年日本学者Kaya 提出了Kaya 恒等式(1),即通过构造链式乘积的形式分解出多个影响因素,将人类活动产生的CO2 与人口、人均GDP、能耗强度等因子联系起来[15],表现为:
| $C{O_2} = \frac{{C{O_2}}}{E} \times \frac{E}{G} \times \frac{G}{P} \times P$ | (1) |
为了囊括更多的有关影响因素,使分解结果进一步合理化,本文对Kaya 恒等式进行了扩展,将分解后的模型变为:
CO2= 各类能源碳排放系数× 各类化石能源占比×GDP 能源消耗量× 人均GDP× 人口规模
即:
| $C{O_2} = \sum\limits_i^{} {} \left( {\frac{{C{O_{2,i}}}}{{{E_{i0}}}} \times \frac{{{E_i}}}{E} \times \frac{E}{G} \times \frac{G}{P} \times P} \right) = \sum\limits_i^{} {} \left( {{F_i} \times {S_i} \times R \times Y \times P} \right)$ | (2) |
其中,CO2,i 为第i 种化石能源消耗产生的CO2排放量(化石能源种类包括煤炭、石油、天然气,下同);Ei 为第i 种化石能源的消耗量;E 为能源消耗总量;G 为剔除物价指数的地区生产总值;P 为地区人口总数;Fi 为第i 种化石能源碳排放量,由碳排放技术因素决定;Si 为第i 种化石能源占能源消费总量的比重,即ΣSi=1,反应能源消费结构;R 为万元GDP 能源消耗量,表示能源消耗强度,即能源效率;Y 为人均GDP(万元),表示人们的生活水平,由经济发展水平决定;P 为人口总数,反应人口规模。
CO2 排放从基期到t 期的绝对变化量为式(3)所示:
| $\begin{array}{l} \Delta C{O_2} = CO_2^t - CO_2^0 = \sum\limits_i^{} {} \left( {F_i^t \times S_i^t \times {R^t} \times {Y^t} \times {P^t}} \right) - \\ \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^0} \times {P^0}} \right) = \\ \left[ {\sum\limits_i^{} {} \left( {F_i^t \times S_i^t \times {R^t} \times {Y^t} \times {P^t}} \right) - \sum\limits_i^{} {} \left( {F_i^0 \times S_i^t \times {R^t} \times {Y^t} \times {P^t}} \right)} \right] + \\ \left[ {\sum\limits_i^{} {} \left( {F_i^0 \times S_i^t \times {R^t} \times {Y^t} \times {P^t}} \right) - \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^t} \times {Y^t} \times {P^t}} \right)} \right] + \\ \left[ {\sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^t} \times {Y^t} \times {P^t}} \right) - \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^t} \times {P^t}} \right)} \right] + \\ \left[ {\sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^t} \times {P^t}} \right) - \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^0} \times {P^t}} \right)} \right] + \\ \left[ {\sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^0} \times {P^t}} \right) - \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^0} \times {P^0}} \right)} \right] + \\ \sum\limits_i^{} {} \left( {\Delta {F_i} \times S_i^t \times {R^t} \times {Y^t} \times {P^t}} \right) + \sum\limits_i^{} {} \left( {F_i^0 \times \Delta {S_i} \times {R^t} \times {Y^t} \times {P^t}} \right) + \\ \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times \Delta R \times {Y^t} \times {P^t}} \right) + \\ \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times \Delta Y \times {P^t}} \right) + \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times {Y^0} \times P} \right) = \\ \Delta C{O_{2,F}} + \Delta C{O_{2,S}} + \Delta C{O_{2,R}} + \Delta C{O_{2,Y}} + \Delta C{O_{2,P}} \end{array}$ | (3) |
其中,ΔCO2 相对于基期CO2,i 排放的绝对变化量;ΔCO2,F 能源碳排放强度效应;ΔCO2,S 能源结构效应;ΔCO2,R GDP 能源强度效应;ΔCO2,Y 生活水平效应;ΔCO2,P 人口规模效应。
1.2 Tapio 脱钩弹性分解模型2005 年日本学者Tapio 构建了用以探究碳排放与经济发展关系的脱钩弹性指标,见式(4),并将其划分为8 种脱钩状态,即Tapio 脱钩指标等级与弹性值见图 1 所示[9]。为了定量分析碳排放与经济发展的关系,将碳排放因素分解模型与Tapio 脱钩弹性指标相结合,构建碳排放Tapio 脱钩弹性分解模型,即将式(3)与式(4)联立可得:
| $\varepsilon = \frac{{\Delta C{O_2}/C{O_2}}}{{\Delta GDP/GDP}}$ | (4) |
| $\begin{array}{*{20}{l}} {\varepsilon = \frac{{\Delta C{O_2}/C{O_2}}}{{\Delta GDP/GDP}} = \sum\limits_i^{} {} \left( {{F_i} \times S_i^t \times {R^t} \times {Y^t} \times {P^t}} \right)\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + }\\ \begin{array}{l} \sum\limits_i^{} {} \left( {F_i^0 \times {S_i} \times {R^0} \times {Y^t} \times {P^t}} \right)\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + \\ \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times \Delta R \times {Y^t} \times {P^t}} \right)\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + \end{array}\\ \begin{array}{l} \sum\limits_i^{} {} \left( {F_i^0 \times S_i^0 \times {R^0} \times \Delta Y \times {P^t}} \right)\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + \\ \sum\limits_i^{} {} \left( {F_i^0 \times {S_i} \times \Delta R \times {Y^t} \times {P^t}} \right)\frac{{GDP}}{{C{O_2} \times \Delta GDP}} = \end{array}\\ {\Delta C{O_{2,F}}\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + \Delta C{O_{2,S}}\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + \Delta C{O_{2,R}}\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + }\\ {\Delta C{O_{2,Y}}\frac{{GDP}}{{C{O_2} \times \Delta GDP}} + \Delta C{O_{2,P}}\frac{{GDP}}{{C{O_2} \times \Delta GDP}} = }\\ {{\varepsilon _F} + {\varepsilon _S} + {\varepsilon _R} + {\varepsilon _Y} + {\varepsilon _P}} \end{array}$ | (5) |
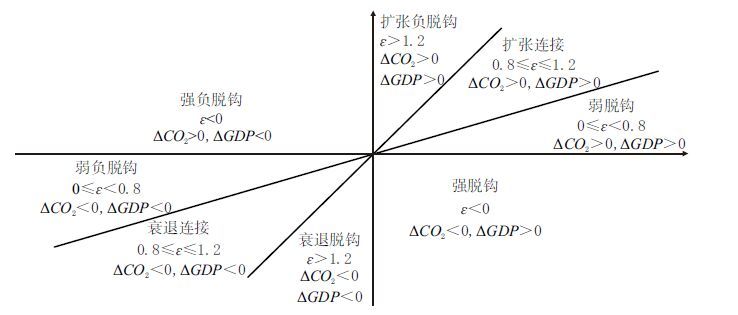 |
| 图1 Tapio 脱钩指标等级与弹性值 |
| 表1 福建省1990-2013 年碳排放各影响因素的脱钩弹性系数值 |
根据构建的Tapio 脱钩弹性分解模型,分别以1990 年、1995 年、2000 年、2005 年和2010 年为基期,将整理后的福建省数据代入式(5),再分别以上一年为基期,计算出2001-2011 年各影响因素的Tapio 脱钩弹性指标值(表 1)及各影响因素的脱钩弹性贡献百分比(%)(表 2),其中由于假设技术水平不变,因而该期间内碳排放系数不变,从而使能源碳排放强度的脱钩弹性系数均为0。
| 表2 福建省1990-2013 年碳排放各影响因素的脱钩弹性贡献率(%) |
由表 1 可以看出,1990-2013 年5 个时期中福建省碳排放脱钩状态大体呈现为V 形分布状态,其中2000-2005 年达到谷底,显现为扩张负脱钩状态;2000 年前和“十一五”时期脱钩状态有所改善,均为弱脱钩状态;而2011 年的脱钩情况再次恶化,2012 年反而实现了理想的强脱钩状态,即总体上看2010 年到2013 年的脱钩状况变化反复。
以具体状况来分析,2000 年前的脱钩状态为弱脱钩,这是由于2000 年前高排放高污染产业还没有完全成为贡献福建省GDP 增长的主力军;而2000年后中国加入世贸组织,逐渐成为世界工厂,加工制造业日益壮大,福建省也不能幸免,造成其碳排放脱钩情况的恶化,因此2001-2005 年的碳排放整体趋向于扩张负脱钩状态;2005 年后低碳行动的日渐展开使得碳排放与经济增长的脱钩情况有所改善,呈现出弱脱钩状态,某种程度上也是完成“十一五”能源规划发展目标而力促所得;2011 年福建省的碳排放脱钩状态再次为扩张负脱钩,2012 年又实现了理想的强脱钩状态,2013 年复为弱脱钩状态,这种反复很大程度是因为“十二五”初期福建省探寻发展道路而做出各种尝试所导致的,此外也不排除“十一五”时期福建省对经济高速增长的强烈追求,忽略能源资源的可持续发展的因素。
从表 2 中各个影响因素的脱钩弹性值占碳排放的总脱钩弹性值的比重来看,εR 和εY 的脱钩弹性贡献百分比的绝对值均较高,可见GDP 能源强度εR 的下降和生活水平εY 的提高对福建省碳排放脱钩的影响较大。但随着GDP 的增长,GDP 能源强度的作用呈现明显的下降趋势,生活水平效应则在“十一五”期间作用骤减,2005 年后又提升至以往水平。人口规模εP 效应在近几年来作用逐渐加强,能源结构εS 对碳排放脱钩的负面贡献作用慢慢变小,能源碳排放强度效应εF 则因内在技术水平的制约基本不变。
由此可以得知,长期以来福建省低碳经济发展较依赖于能源强度的降低,主要是由于经济增长和化石能源消耗减少,尤其是高耗能、高排放的主导产业减排工作的进行使能源消费有了节制,但这些高耗能、高排放、低效率的产业仍旧是福建省的支柱产业,对福建省的经济增长起着重要作用,且其减排的工作尚处于表面层次,没有完全深入,因而进一步脱钩还有很大空间;能源结构效应对福建省碳排放与经济增长脱钩的作用主要体现在结构的优化上,特别是与2004 年起天然气的全面引进,以及近几年来风、核、水电等清洁能源的倡用有着很大的关系,但与其他地区比较起来,福建省能源结构优化的速度还是比较缓慢且有所反复的;人们生活状况的改善反而恶化了碳排放与经济增长的脱钩,尚未全员步入小康社会的福建人民生活水平提高,消费扩大,使得生产增加,能源消耗也相应增加;人口规模效应也同样如此。可见,福建省要实现碳排放脱钩,还是要切实加强碳减排工作,提高人们低碳意识,降低能源强度,调整能源消费结构,加大科研技术研发力度,从根本上解决能源碳排放强度居高不下的现状。
2 碳排放脱钩前景预测与情景分析从碳排放角度看,根据福建省“十二五”能源规划发展目标,假定2015 年时各指标均恰好达标,即一次能源消费量年均增长7.6%(其中煤炭、石油、天然气年均分别增长7%、8% 和24.6%),此时可以计算得到2015 年福建省的碳排放总量为29 826.25 万吨。从经济增长的角度看,一方面福建省“十二五”经济发展规划目标要求2010-2015 年期间福建地区生产总值年均增长10%,假定2015 年时恰好达标,则2015 年福建省GDP 将达21 054.9 亿元;另一方面,如果经济总量以往年的趋势增长,那么在过去十年里福建省GDP 的平均增速高达12.4% 的情况下,2015 年福建省的GDP 将达21 985.4 亿元。因此,若上述一次能源消费量各指标均实现“十二五”规划发展目标,即2015 年碳排放量为29 826.25 万吨,则在这两种经济增长预测值下2010-2015 年福建省碳排放脱钩弹性指标值分别为0.59 与0.65,状态均为弱脱钩,但前者的脱钩弹性指标值相较于2005-2010 时期有所改善,而后者则相对恶化了。此外,在2010 年福建省碳排放强度为1.65 吨CO2/万元的基础上,前一种GDP 预测值下的2015年福建省碳排放强度为1.42 吨CO2/万元,相比2010年下降13.9 个百分点,也就是说没有实现“十二五”规划中GDP 碳排放降低17% 的能源发展目标要求;而后一种GDP 预测值下的碳排放强度为1.36吨CO2/万元,相比2010 年约降低了17.5%,虽达到“十二五”规划中GDP 碳排放降低17% 的要求,但其降幅却很大一部分归功于经济的快速增长,而不是能耗的节约或碳排放的减少。
本文以满足国家“十二五”规划纲要中碳排放强度降低17% 的要求出发,在以不同增速对经济增长进行预测的前提下,根据碳排放因素分解模型对能源消耗总量、结构进行不同比例和方向的调整,设计出不同的碳排放情景,并对碳排放与经济增长的脱钩情况进行分析。鉴于自2001 年以来福建省人口自然增长率为7.63‰,符合人口“十二五”专项规划要求,以及目前有关人口政策的不确定性和模型分析的简洁简便性,此处不考虑人口变化与增长对经济增长、碳排放及脱钩状态的影响,即将碳排放因素分解模型式(2)变为式(6)。相应的,CO2 排放绝对变化量(3)与Tapio 脱钩弹性分解模型式(5)变为式(7)、式(8)。根据式(6)、(7)、(8)因素分解计算出实现“十二五”期间碳排放强度降低17% 发展目标的5 种情景(表 3)。
| $C{O_2} = \frac{{C{O_{2,i}}}}{{{E_i}}} \times \frac{{{E_i}}}{E} \times \frac{E}{G} \times G = {F_i} \times {S_i} \times R \times G$ | (6) |
| $\Delta C{O_2} = \Delta C{O_{2,F}} + \Delta C{O_{2,S}} + \Delta C{O_{2,R}} + \Delta C{O_{2,G}}$ | (7) |
| $\varepsilon = \frac{{\Delta C{O_2}/C{O_2}}}{{\Delta GDP/GDP}} = {\varepsilon _F} + {\varepsilon _S} + {\varepsilon _R} + {\varepsilon _G}$ | (8) |
| 表3 2015 年碳排放强度下降17% 约束下的情景假设* |
情景假设中的主要变量为GDP 年均增速与一次能源消费结构。情景1 假设GDP 年均增速与能源消费结构均满足“十二五”规划目标,碳排放强度下降17% 的约束下,化石能源消费总量为11 878万吨标准煤;情景2 中GDP 增速满足“十二五”规划发展要求,能源消费总量为11 809 万吨,此时一次能源消费结构不满足“十二五”能源规划要求,而是以福建省2013 年一次能源消费结构的比例为假定条件,即以历史趋势演进。此时观察情景1 和情景2 在表 3 中的数据发现,在GDP 年均增速为10%时,即使能源消费结构如“十二五”规划要求进行了优化,此时两者的化石能源消费总量却相距不大,因而这两种情景所能达到的脱钩水平是一致的。
情景3 假设GDP 年均增速以往年历史趋势增长,而能源消费结构满足“十二五”要求,得出能源消费量达12 403 万吨,可见此时经济发展在能源消耗中起到相当重要的作用;情景4 假设两者均以历史趋势演进,以作为其他情景的参照。与情景1 和情景2 相似,在GDP 增速均为12.4% 的情况下,一次能源消费结构不同的情景3 与情景4 的脱钩水平亦是一致的,且由于其经济增长更快因而脱钩水平更不理想。
比较情景1 与情景3 发现,在一次能源消费结构满足“十二五”规划要求时,若GDP 增速从历史趋势12.4% 下降到10%,那么化石能源消费总量可以得到较大的减少;同理,比较情景2 与情景4 亦发现即使一次能源消费结构保持2013 年的状态,但经济增长若能放缓,则化石能源消费量仍能够有效降低,进而脱钩水平也能够从0.60 提高到0.58。因此,根据GDP 增速相同而能源消费结构不同的两组情景比较结果发现,若是能源消费结构的优化程度仅达到“十二五”规划的最低要求,则对化石能源消费量的降低并不能起到较大作用,因而不能有效促进经济增长与碳排放的脱钩;另一方面,根据一次能源消费结构相同而GDP 增速不同的两组情景比较发现,若经济增长放缓便能有效减少化石能源的消费,从而促进碳排放脱钩水平的提升。由此设定情景5:GDP 增速进一步降低为8%,一次能源消费结构进一步优化为50:20:8:22(表 3),此时2015年碳排放脱钩状态虽仍为弱脱钩,但弹性值有所减小,显现出经济低增长、能源结构深优化的状态。
综上所述,可知前4 种情景对于实现“十二五”规划目标是力乏的,并不能有效实现经济增长与碳排放的脱钩。而鉴于2010 年来福建省经济的高增长、能源的高消耗与产业结构和能源结构的反优化发展,我们认为应以碳排放强度的降低为衡量低碳经济发展水平的最高指标,因为碳排放强度的降低则意味着碳排放与经济增长脱钩状况的改善,意味着在此情境下实现碳减排是一种帕累托改进。结合实际,考虑到目前福建省由于工业化与城镇化进程的深入而产生对能源的刚性需求,不必强求于能源强度的大幅度下降,要着重于从战略上发展低耗能、低排放的新兴产业,引导高消耗、高排放的三大主导产业的技术转型,结构上倾向于第三产业的增长,能源上注重消费结构的优化。总之,在2013 年发展基础上,福建省在余下的“十二五”时期里应以情景假设5 为较可行方案,倡行增速不高于10% 的经济较低增长与非化石能源占比不低于20% 的消费结构深优化,在把握住碳排放强度降幅大关的同时,追求经济增长从依赖工业到倚重第三产业,力争能源消费类型向清洁能源转化,最终向实现碳排放与经济增长的强脱钩迈进。
3 结论与建议总的来说,要实现未来一段时期里福建省经济增长与CO2 排放的脱钩,确保可行方案在经济发展中的实现,余下的“十二五”时期里不能再单纯追求经济总量的高速增长,甚至还要用总量的些许牺牲来换取产业结构的升级转型;在此基础上,要实现“十二五”发展目标,又要满足工业化、城镇化进程中对能源的刚性需求,未来时期里还必须注重能源结构的调整优化,尤其注重对非化石能源的投资开发。具体说来,要实现经济增长与碳排放的脱钩,应做到以下几方面:
首先,在制定碳减排计划时,应以碳排放强度为主要指标,以追求碳排放强度的降低为最高标准,并将其纳入行政人员政绩的考核项目中,在追求经济增长的同时注重万元GDP 中CO2 排放量的减少,甚至牺牲部分的经济增长来换取碳排放强度的降低。
其次,有鉴于当前工业化与城镇化引致的能源刚性需求,一方面要从产业结构上减少经济发展中对能源的需求,优先发展低能耗、低排放、高效率的产业,尤其是加大对第三产业中金融、服务业的发展,大力发展战略新兴技术产业,并对三大主导产业进行技术的转型升级,减少高耗能、高排放企业产品的生产和出口[17],从根源上进行碳减排,实现结构节能,追求产业结构的低碳化转型;另一方面也不能单纯追求能源强度的降低,要转变能源消费结构,充分利用福建省沿海靠海优势,大力发展清洁能源产业,开发风能、水能、核能等清洁能源来替代煤炭、石油等高排放能源[18],提高非化石能源消费比例。与此同时,斥资对碳排放技术进行转型和升级,引进、消化和吸收国外最新的成熟低碳技术,从长远考虑上进行节能,从而实现技术减排[19]。
最后,福建省在执行这一追求经济增长与碳排放脱钩的可行方案时不能闭关锁国,也不能鼠目寸光,既要向其他低碳经济转型区学习,与之合作,引进先进的减排知识和技术,也要让自身的减排经验走出去。同时,要将经济增长与碳排放的脱钩作为长期的发展目标,列入增长目标,写进发展规划,追求资源、环境与经济的长期可持续低碳化发展。
| [1] | Wang Can, Chen Jining, Zou Ji. Decomposition of energy-related CO2>0 emission in China: 1957-2000[J]. Energy, 2005 (30) : 73 . |
| [2] | 徐国泉, 刘则渊, 姜照华. 中国碳排放的因素分解模型及实证分析: 1995-2004[J]. 中国人口. 资源与环境, 2006 (6) : 158 . |
| [3] | 朱勤, 彭希哲, 陆志明, 等. 中国能源消费碳排放变化的因素分解及实证分析[J]. 资源科学, 2009 (12) : 2072 . |
| [4] | 唐建荣, 张白羽, 王育红. 基于LMDI 的中国碳排放驱动因素研究[J]. 统计与信息论坛, 2011 (11) : 19 . |
| [5] | 雷厉, 仲云云, 袁晓玲. 中国区域碳排放的因素分解模型及实证分析[J]. 当代经济科学, 2011 (5) : 59 . |
| [6] | 张纪录. 区域碳排放因素分解及最优低碳发展情景分析以中部地区为例[J]. 经济问题, 2012 (7) : 126 . |
| [7] | 郝丽, 姜创业, 孙娴, 等. 陕西省能源消费碳排放影响因素分析与政策启示[J]. 水土保持研究, 2013 (6) : 326 . |
| [8] | Organization for economic co-operation and development( OECD).Indicators to measure decoupling of environmental pressure and economic growth[R].Paris: OECD, 2002. |
| [9] | Tapio P. Towards a theory of decoupling: degrees of decoupling in the EU and the case of road traffic in finland between 1970 and 2001[J]. Journal of Transport Policy, 2005 (12) : 137 . |
| [10] | 李忠民, 庆东瑞. 经济增长与二氧化碳脱钩实证研究以山西省为例[J]. 福建论坛: 人文社会科学版, 2010 (2) : 67 . |
| [11] | 李忠民, 姚宇, 庆东瑞. 产业发展、GDP 增长与二氧化碳排放脱钩关系研究[J]. 统计与决策, 2010 (11) : 108 . |
| [12] | 李忠民, 宋凯, 孙耀华. 碳排放与经济增长脱钩指标的实证测度[J]. 统计与决策, 2011 (14) : 86 . |
| [13] | 刘怡君, 王丽, 牛文元. 中国城市经济发展与能源消耗的脱钩分析[J]. 中国人口, 资源与环境, 2011 (1) : 70 . |
| [14] | 王云, 张军营, 赵永椿, 郑楚光. 基于CO2>0 排放因素模型的脱钩指标构建与评估以山西省为例[J]. 煤炭学报, 2011 (3) : 507 . |
| [15] | 王云. 低碳经济“脱钩”量化分解模型研究基于 IPAT 方程的分析[J]. 经济问题, 2012 (5) : 8 . |
| [16] | 吴文洁, 王小妮. 陕西碳排放与经济增长关系研究基于EKC 与脱钩理论[J]. 西南石油大学学报: 社会科学版, 2011 (6) : 69 . |
| [17] | 金乐琴, 刘瑞. 低碳经济与中国经济发展模式转型[J]. 经济问题探索, 2009 (1) : 84 . |
| [18] | 付允, 马永欢, 刘怡君, 等. 低碳经济的发展模式研究[J]. 中国人口, 资源与环境, 2008 (3) : 14 . |
| [19] | 杨嵘, 常烜钰. 西部地区碳排放特征及发展低碳经济途径分析[J]. 西南石油大学学报: 社会科学版, 2012 (1) : 17 . |
 2015, Vol. 17
2015, Vol. 17
