中国是世界猪肉消费第一大国,猪肉是我国居民肉食的主要来源,在我国居民的膳食结构中扮演着重要角色[1]。在传统生猪养殖中,饲养人员往往采取放养或者小规模圈养,随着人民生活水平的提高,人口不断增长,我国对猪肉的需求量大大增加,猪肉的质量安全也需要把关[2]。在现代养殖场中,猪只养殖密度大,人员工作任务繁重,整体效率较低,信息化与生猪产业的深度融合已成为必然趋势,以移动网络、物联网、云计算、大数据分析和人工智能等为代表的理论与技术在世界范围内得到了蓬勃发展和广泛应用,给畜禽养殖业带来了科技保障。生猪状态含有丰富信息,可以一定程度上反映生猪的健康情况。国内外结合计算机相关理论和技术早已对生猪状态及行为有一定的研究,主要集中在母猪生产、仔猪精细管理[3-4]和生猪疾病健康预警领域[5-6],而对于猪只生命周期中的多种状态及行为的研究相对较少。生猪音频是伴随猪只生命周期的一种信息,包含大量语义,能够反映猪只的状态及行为。国内外对生猪的音频研究主要集中于端点检测以及不同状态下的音频识别[7-11]。然而在利用现代信息技术[12]对生猪音频进行监测识别时,由于环境、经济条件的限制,养殖人员往往将多头生猪圈养在一起,这就导致了采集到的识别源为多头生猪共同发出的混合音频,不利于音频的特征提取及识别。为了尽可能从混合生猪音频信号中分离出各源信号分量,提取有效特征,盲源分离成为了一种有效的解决办法。
盲源分离(blind source separation, BSS)是从由多个麦克风捕获到的混合信号中恢复未知的源信号,其普遍应用于语音处理、生物医学信号处理、机械故障等领域[13-15],依据源信号的数目小于、等于或大于麦克风的数目,盲源分离可分为超定、正定和欠定3种情况。考虑到养殖场的生猪数量较多,而采集设备数量较少,因此本研究重点关注欠定情况下的盲源分离。由于一些理论算法实用性较弱,欠定盲源分离问题在盲源分离中依然具有挑战性。近年来,国内外一般基于稀疏分量分析(sparse component analysis, SCA)[16-17]的方法来解决欠定盲源分离问题;Chen等[18]通过求解大规模线性规划问题,获得信号在过完备基中的稀疏表示;Bofill和Zibulevsky[19]提出了基于SCA的两步法,从两种混合音频中分离出了6个源信号,该方法算法复杂度较低,易得到全局收敛值;Georgiev等[20]采用稀疏分量分析方法对稀疏信号进行分离,并与文献[18]中的方法做对比,得到了更优的结果。源信号的稀疏性对于SCA算法的重要性不言而喻,许多时频域的扩展算法被提出来以增强和充分利用信号的稀疏性。Zhen等[21]发现并证明了单源点主导的时频点与一维子空间有关,采用分层聚类算法得到混合矩阵的估计,并通过求解一系列最小二乘问题来恢复源信号;Jourjine等[22]提出了一种简并混合估计技术,并在语音信号和无线信号上验证了该方法能够实现混合源信号的分离;Xie等[23]提出了一种改进的信息论准则方法来检测欠定情况下的源数,利用四阶张量盲辨识方法对混合矩阵进行估计,采用一种lp范数分集测度方法对源信号重构,获得了较好的分离结果,并且运行速度快;Arberet等[24]利用局部置信度测量的统计模型检测出单源点的时频区域,并利用DEMIX聚类算法,将来自所有时频区域的信息根据其置信度进行合并,以完成混合矩阵的估计;Hassan和Ramli[25]引入自适应时频阈值来提高欠定盲源分离中混合矩阵的精度,结果表明该方法较优,且耗时较少。于和新[26]针对非稀疏信号的线性混合欠定盲源分离问题提出了一种时频两步法,通过数值试验与分析证明了该算法具有有效性和准确性。国内外对欠定盲源信号分离的音频试验主体往往为函数信号,而对于实际应用的音频信号方面研究较少。
本研究基于“两步法”的SCA,提出了一种基于稀疏化理论的欠定生猪盲源信号分离改进方法,拟解决在生猪音频识别实际应用时采集到的识别源特征难以提取的问题。
1 材料与方法 1.1 总体设计本研究的总体设计流程如图 1所示,首先获取生猪混合音频信号,然后利用信号的稀疏性提取单源特征点,并用聚类算法估计音频混合矩阵,最后通过重构算法分离出各音频源信号。

|
图 1 研究技术路线 Fig. 1 Research technical route |
本研究根据所提算法,针对欠定生猪盲源信号分离问题,在MATLAB仿真环境中做了一些试验。在试验设计上,“2.1”节中,选取生猪的3种声音,说明3个源信号和2个观测信号下不同时长的欠定生猪盲源信号分离的一般过程;“2.2”节选取另外5段15 s左右不同状态的单声道音频,设置不同数量的源信号与观测信号以及幅值衰减矩阵,比较重构信号与源信号在第“1.7”节的测量指标,来验证算法的性能。
1.2 试验材料及获取本研究运用NanoPc-T4作为主控制器,外接iTalk-02麦克风、USB接口等资源,自主实现声音采集传输的硬件系统。音频格式设置为WAV,采样大小为8位,采样率为44.1 kHz,试验使用的声音主要源于安徽蒙城京徽蒙养猪场的成年长白猪,音频在较为安静的空间中获取并经过卡尔曼滤波降噪处理。
1.3 欠定盲源分离模型欠定盲源分离(underdetermined blind source separation, UBSS)问题的线性瞬时混合模型可以表示为:
| $\boldsymbol{X}_{\mathrm{N}}(\mathrm{t})=\sum\limits_{m=1}^{\mathrm{M}} \boldsymbol{a}_{\mathrm{nm}} \boldsymbol{S}_{\mathrm{m}}\left(\mathrm{t}-\mathrm{t}_{\mathrm{nm}}\right)+\boldsymbol{n}(\mathrm{t}) \quad \mathrm{M}>\mathrm{N}$ | (1) |
式中,XN(t)=[x1(t), x2(t), …, xn(t)]表示观测信号向量,Sm(t-tnm)表示经过时延tnm到达传感器的源信号向量,n(t)表示噪声,anm为幅值衰减矩阵,表示信号的衰减系数。本研究暂不考虑噪声带来的影响。
1.4 音频信号稀疏化及单源点提取信号的稀疏性是指其在大多数时刻幅值为零,而在小部分时刻的幅值较大。根据文献[27]中对混合信号可恢复性分析可知,信号在时域或者变换域中越稀疏,每个源信号能被正确分离出来的概率就越高。由于信号在时频域稀疏性更强,本研究采用短时傅里叶变换对混合生猪音频信号进行时频域转换[19]。
稀疏信号的性质决定了同一时刻出现两个源信号取值非零可能性很小,根据非平稳信号的短时平稳性质可知,一定存在一个频率不变、时间相邻的单源点邻域U(t, f),在此邻域内的点都是由同一路源信号si主导的,如果能够从混合信号中提取足够的单源点,那么由单源点组成的散点图会清晰地聚集在N条直线附近[28-29],采用聚类算法就可以实现混合矩阵的估计。在不考虑噪声的前提下,式(1)可以展开为:
| $\begin{array}{c} \left(\begin{array}{c}\boldsymbol{x}_1(\mathrm{t}) \\ \boldsymbol{x}_2(\mathrm{t}) \\ \vdots \\ \boldsymbol{x}_n(\mathrm{t})\end{array}\right)=\left(\begin{array}{c}\boldsymbol{a}_{11} \\ \boldsymbol{a}_{21} \\ \vdots \\ \boldsymbol{a}_{\mathrm{n} 1}\end{array}\right) \boldsymbol{s}_1(\mathrm{t})+\left(\begin{array}{c}\boldsymbol{a}_{12} \\ \boldsymbol{a}_{22} \\ \vdots \\ \boldsymbol{a}_{n 2}\end{array}\right) \boldsymbol{s}_2(\mathrm{t})+\cdots+ \\ \left(\begin{array}{c}\boldsymbol{a}_{1 \mathrm{~m}} \\ \boldsymbol{a}_{2 \mathrm{~m}} \\ \vdots \\ \boldsymbol{a}_{\mathrm{nm}}\end{array}\right) \boldsymbol{s}_{\mathrm{m}}(\mathrm{t})\end{array}$ | (2) |
假设t时刻,只有源信号si(t)取值很大,则式(2)可以近似为:
| $\begin{array}{c} \left(\begin{array}{c}\boldsymbol{x}_1(\mathrm{t}) \\ \boldsymbol{x}_2(\mathrm{t}) \\ \vdots \\ \boldsymbol{x}_n(\mathrm{t})\end{array}\right)=\left(\begin{array}{c}\boldsymbol{a}_{1 \boldsymbol{i}} \\ \boldsymbol{a}_{2 \boldsymbol{i}} \\ \vdots \\ \boldsymbol{a}_{\mathrm{ni}}\end{array}\right) \boldsymbol{s}_1(\mathrm{t}) \Leftrightarrow \frac{\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})}{\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})}= \\ \frac{\operatorname{Im}\left(\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})\right)}{\operatorname{Im}\left(\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})\right)}=\frac{\operatorname{Re}\left(\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})\right)}{\operatorname{Re}\left(\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})\right)}=\frac{\boldsymbol{a}_{1 \mathrm{i}} \boldsymbol{s}_{\mathrm{i}}}{\boldsymbol{a}_{2 \mathrm{i}} \boldsymbol{s}_{\mathrm{i}}}=\frac{\boldsymbol{a}_{1 \mathrm{i}}}{\boldsymbol{a}_{2 \mathrm{i}}}\end{array}$ | (3) |
式中,xi(t, f)为第i个观测信号在时频域的复数表示,Re(.)和Im(.)分别表示实部与虚部。由式(3)可知,源信号si(t)所有取值非零的时刻将确定一条方向为混合矩阵A的第i个列向量的直线,且单源点的实部与虚部比值为定值,因此可以用式(4)作为单源点的判据:
| $\frac{\operatorname{Im}\left(\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})\right)}{\operatorname{Re}\left(\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})\right)}=\frac{\operatorname{Im}\left(\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})\right)}{\operatorname{Re}\left(\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})\right)}$ | (4) |
然而由于噪声和计算误差以及大量低能点(聚集在零点附近的点)的影响,仅凭式(4)提取到的单源点的空间分布会与混合矩阵A对应的列方向有所偏差,导致估计的混合矩阵误差较大。针对这一问题,本研究首先使用式(5)放宽约束条件来初步筛选单源点:
| $\left|\frac{\operatorname{Im}\left(\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})\right)}{\operatorname{Re}\left(\boldsymbol{x}_1(\mathrm{t}, \mathrm{f})\right)}-\frac{\operatorname{Im}\left(\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})\right)}{\operatorname{Re}\left(\boldsymbol{x}_2(\mathrm{t}, \mathrm{f})\right)}\right|<\varepsilon_1$ | (5) |
式中, ε1为设置的阈值。检测同一频域内相邻M个点的均值x(tM, fM) (式(6))和方差var[xM](t, f)(式(7)),以方差小于阈值ε2为衡量准则,进一步筛选为单源点,最后计算单源点的l2范数‖x(t, f)i‖2(式(8)),以其值小于设定的阈值σ来剔除低能点。
| $\bar{x}\left(\mathrm{t}_{\mathrm{M}}, \mathrm{f}_{\mathrm{M}}\right)=\frac{1}{\mathrm{M}} \sum\limits_{\mathrm{m}=1}^{\mathrm{M}} \boldsymbol{x}\left(\mathrm{t}_{\mathrm{m}}, \mathrm{f}_{\mathrm{m}}\right)$ | (6) |
| $\operatorname{var}\left[\boldsymbol{x}_{\mathrm{M}}\right](\mathrm{t}, \mathrm{f})=\frac{1}{M-1} \sum\limits_{\mathrm{m}=1}^{\mathrm{M}}\left|\boldsymbol{x}\left(\mathrm{t}_{\mathrm{m}}, \mathrm{f}_{\mathrm{m}}\right)-\bar{x}\left(\mathrm{t}_{\mathrm{M}}, \mathrm{f}_{\mathrm{M}}\right)\right|^2$ | (7) |
| $\left\|\boldsymbol{x}(\mathrm{t}, \mathrm{f})_{\mathrm{i}}\right\|_2<\sigma$ | (8) |
在获得足够的单源点后,可以使用聚类算法对特征点进行聚类以估计混合矩阵,传统的聚类算法有K-means、模糊聚类(fuzzy clustering-means, FC-means)等,尽管这些经典的方法的精度高、计算速度快,但其聚类结果对初始聚类中心比较敏感,且聚类个数需要已知,与实际盲源分离中源信号个数未知不符。相比之下,近邻传播聚类算法不需要指定最终聚类族的个数,其簇中心点是已有的数据点,且结果的平方差误差较小,正好弥补了这一问题。AP聚类将所有样本点都视为潜在的聚类中心,通过循环迭代选取中心点,得到最优的类代表簇,然而其聚类结果受超参阻尼系数的影响且算法复杂度较高,因此,本研究结合奇异值分解,提出一种自适应阻尼系数的AP聚类算法来估计混合矩阵。
1.5.1 奇异值分解 由于提取的单源点一般为总体采样点的20%~40%,这使得AP聚类在构造相似矩阵时得到的矩阵维度较大,需要大量内存,且计算复杂度较高。为了加快算法的计算速度,本研究引入奇异值分解(singular value decomposition, SVD)来降维以减少复杂度,对矩阵A的奇异值分解定义如下:
| $\boldsymbol{A}^{\prime}=\boldsymbol{U} \boldsymbol{\varSigma} \boldsymbol{V}^{\mathrm{T}}$ | (9) |
式中, Σ为N阶对角矩阵,其对角线上的元素为从小到大排序的奇异值σi;U和V为N阶正交矩阵,U的列元素为左奇异向量,V的列元素为右奇异向量,分别由A′A′T和A′TA′的特征向量组成。由于本研究构造的相似矩阵为对称矩阵,因此,式(9)可写成:
| $\boldsymbol{A}^{\prime}=\boldsymbol{U} \boldsymbol{\varSigma} \boldsymbol{U}^{\mathrm{T}}$ | (10) |
经过奇异值分解后,对矩阵A做低秩近似操作,保留Σ中最大的k个奇异值,k值的设定依据式(11),定义错失率ER为:
| $\mathrm{ER}=\left(1-\frac{\sum\limits_{\mathrm{i}=1}^{\mathrm{k}} \boldsymbol{A}_{\mathrm{ii}}}{\sum\limits_{\mathrm{i}=1}^{\mathrm{n}} \boldsymbol{A}_{\mathrm{ii}}}\right) \times 100 \%$ | (11) |
当ER小于10%时,认为k的取值合理。将剩余奇异值置为0,结合左右对应的奇异向量来近似描述矩阵A:
| $\boldsymbol{A}_{\mathrm{N} \times \mathrm{N}}^{\prime}=\boldsymbol{U}_{\mathrm{N} \times \mathrm{N}} \sum\limits_{\mathrm{N} \times \mathrm{N}} \boldsymbol{U}_{\mathrm{N} \times \mathrm{N}}^{\mathrm{T}} \approx \boldsymbol{U}_{\mathrm{k} \times \mathrm{k}} \sum\limits_{\mathrm{k} \times \mathrm{k}} \boldsymbol{U}_{\mathrm{k} \times \mathrm{k}}^T=\boldsymbol{A}^{\prime \prime}$ | (12) |
经过式(12)低秩近似处理后,A变为秩为k的矩阵A″。
1.5.2 AP聚类算法 AP聚类算法以对数似然作为样本点间的相似度度量,一般采用负的欧式距离来计算样本点间的相似度[30],然而欧氏距离容易受量纲影响,并且不能体现特征点在方向上的特性。因此本研究引入负的余弦距离来构造特征相似度矩阵,其计算公式为:
| $\mathrm{S}(\mathrm{i}, \mathrm{k})=-\frac{\mathrm{x}_{\mathrm{i}} \cdot \mathrm{x}_{\mathrm{k}}}{\left\|\mathrm{x}_{\mathrm{i}}\right\|_2 \cdot\left\|_{\mathrm{x}_{\mathrm{k}}}\right\|_2}$ | (13) |
式中, xi和xk为第i和k个点。
相似矩阵对角线上的元素为偏向参数p,其值较大的样本点容易选取为集群中心(称为范例),将所有相似度值的中位数提取出来并赋值给S主对角线上的所有元素,以保证每个数据点成为范例的可能性相等[31-32]。
为了找到合适的聚类中心,定义吸引度矩阵R(i, k)描述点k适合作为点i的聚类中心的程度,归属度矩阵A(i, k)描述点i选择点k作为聚类中心的合适程度,选择合适大小的零矩阵对R和A初始化,样本点间通过归属度和吸引度两种消息不断传递更新,寻找到最优的聚类中心。式(14)、(15)分别为吸引度矩阵R和归属度矩阵A的更新规则:
| $\boldsymbol{R}(\mathrm{i}, \mathrm{k})=\boldsymbol{S}(\mathrm{i}, \mathrm{k})-\max _{\mathrm{k}^{\prime} \neq \mathrm{k}}\left(\boldsymbol{A}\left(\mathrm{i}, \mathrm{k}^{\prime}\right)+\boldsymbol{S}\left(\mathrm{i}, \mathrm{k}^{\prime}\right)\right)$ | (14) |
| $\boldsymbol{A}=\left\{\begin{array}{l}\boldsymbol{A}_{t+1}(\mathrm{k}, \mathrm{k})=\sum\limits_{\mathrm{i}^{\prime} \neq \mathrm{k}} \max \left(0, \boldsymbol{R}_{\mathrm{t}}\left(\mathrm{i}^{\prime}, \mathrm{k}\right)\right) \\ \boldsymbol{A}_{\mathrm{t}+1}(\mathrm{i}, \mathrm{k})=\min \left(0, \boldsymbol{R}_{\mathrm{t}}(\mathrm{k}, \mathrm{k})+\right. \\ \qquad \sum\limits_{\left.\mathrm{i}^{\prime} \notin \mathrm{i}, \mathrm{k}\right\}} \max \left\{0, \boldsymbol{R}_{\mathrm{t}}\left(\mathrm{i}^{\prime}, \mathrm{k}\right)\right\})\end{array}\right.$ | (15) |
式中, t表示当前迭代次数,i, k为不同行列的索引值。式(14)表明,任意一个候选聚类中心都可以对其他候选聚类中心产生影响,并且可以争夺其他点的归属权,在第一次迭代时,由于A的初值为零,所以R的更新不考虑其他点对于候选范例的影响;在后面的迭代中,当一些点被有效地分配给其他范例时,它们的归属度值依据式(15)的更新规则将降为负数,这将减少式(14)中输入相似度的有效值,在竞争中移除相应的候选样本;若R(k, k)最终是负值,则说明点k更适合归属于其他范例而本身不适合作为一个范例。式(15)中,归属度A(i, k)的更新规则为自我吸引度加上从其他点获得的积极的吸引度,这里只加上积极(数值为正)的吸引度是因为只有积极的吸引度才会支持点k作为聚类中心;自我归属度A(k, k)的值为从其他点获得的积极吸引度之和,若A(k, k)为负值,则说明点k目前更适合归属于另一个范例,而不是作为一个范例本身。
由于更新消息的过程中容易出现数值振荡,使得算法不易收敛,引入阻尼系数(damping factor, DF)来衰减吸引度信息和归属度信息,采用公式(16)、(17)更新R和A:
| $\boldsymbol{R}=(1-\lambda) \times \boldsymbol{R}+\lambda \times \boldsymbol{R}_{\text {old }}$ | (16) |
| $\boldsymbol{A}=(1-\lambda) \times \boldsymbol{A}+\lambda \times \boldsymbol{A}_{\text {old }}$ | (17) |
式中,Rold表示上一次更新的吸引度矩阵;Aold表示上一次更新的归属度矩阵;λ∈[0, 1],表示为阻尼系数。
通过设定最大迭代次数m来终止算法,同时设置迭代终止次数n,即在没达到最大迭代次数m的前提下,经过连续迭代n次后,聚类中心始终没有改变,此时认为算法已收敛,聚类中心已确定。以矩阵R和A对角线元素之和大于0为衡量准则,确定范例,以相似度为衡量,确定其他点归属为哪一范例。将每类簇中心的单位方向向量提取出来,完成混合矩阵的估计。
1.5.3 自适应阻尼系数法 阻尼系数λ取不同的值会影响算法的全局和局部搜索能力,进而对算法的收敛性能产生干扰。传统AP聚类时,阻尼系数往往基于先验经验设定为固定值,这使得算法在不同阶段无法动态地调节搜索性能,为此本研究提出了一种动态的阻尼系数自适应方法。
采用一个长度为L的移动窗,比较当前迭代时的聚类数目和上一次迭代的聚类数目是否下降或一致,是则记为1,否则记为0,考虑到算法初始阶段的不稳定以及偶尔出现的少量震荡情况,认为超过2/3的记录显示为0时,发生了振荡,此时,对阻尼系数λ进行调整,考虑算法的收敛性,将λ的初始值设定为系统默认值0.5,当到达最大值时不再增加,具体调整规则为:
| $\lambda=\lambda_{\text {old }}+0.01 \quad \lambda \in[0.5, 1]$ | (18) |
式中,λold表示上一次迭代使用的阻尼系数值。
1.5.4 聚类评价指标 轮廓系数(silhouette coefficient)是一种衡量聚类结果的指标,它反映了一个样本与同簇中其他样本的相似度与不同簇中样本的相似度之间的差异。轮廓系数越接近1,表明聚类结果的效果越好;轮廓系数越接近-1,表明聚类结果的效果越差。本研究使用轮廓系数来衡量自适应SVD-AP聚类的效果,它的计算公式为:
| $\mathrm{SC}(\mathrm{i})=\frac{\mathrm{b}(\mathrm{i})-\mathrm{a}(\mathrm{i})}{\max \{\mathrm{a}(\mathrm{i}), \mathrm{b}(\mathrm{i})\}}$ | (19) |
式中,a(i)为向量i与类内所有其他样本的平均距离,b(i)为向量i到其他每个类中样本平均距离的最小值。
1.6 生猪音频源信号重构由于欠定情况下估算得到的混合矩阵是一个非满秩的矩阵,因此无法直接通过估算的矩阵实现源信号的重建。本研究采用一种基于稀疏性的方法来重构源信号,考虑式(1)所示的瞬时线性混合模型,在混合矩阵α已经估计出的情况下,稀疏源信号S的估计问题可以转化为如下的优化问题:
| $\hat{\boldsymbol{S}}=\operatorname{argminJ}_{\mathrm{p}}(\boldsymbol{S}), \quad$ s. t. $\boldsymbol{a} \boldsymbol{S}=\boldsymbol{X}$ | (20) |
式中,
| $\|\boldsymbol{s}\|_{\mathrm{p}}=\left(\sum\limits_{\mathrm{i}=1}^{\mathrm{n}}\left|\boldsymbol{s}_{\mathrm{i}}\right|_{\mathrm{p}}\right)^{1 / \mathrm{p}} \quad \mathrm{p} \in(0, 1]$ | (21) |
式中,p为设定的值。本节基于lp范数完成对生猪音频的重构。
假设源信号与观测信号数目分别为M、N,则lp范数解中最多有M个非零值[34-35],对于每个采样点可以获得CMN个可能解,通过比较这些可能解的lp范数就可以得到最小化lp范数解。整个算法步骤可简要描述如下:
1) 求出混合矩阵a的CMN个N×N维子矩阵
2) 对于某一时刻t,求解lp范数最小化问题的可能解:
| $\hat{\boldsymbol{S}}^{(\mathrm{k})}(\mathrm{t})=\left\{\begin{array}{l} {\left[\hat{\boldsymbol{S}}_{\mathrm{k} 1}{ }^{(\mathrm{k})}(\mathrm{t}), \hat{\boldsymbol{S}}_{\mathrm{k} 2}{ }^{(\mathrm{k})}(\mathrm{t}), \cdots, \hat{\boldsymbol{S}}_{\mathrm{kN}}{ }^{(\mathrm{k})}(\mathrm{t})\right]^{\mathrm{T}}=} \\ \qquad \hat{\boldsymbol{A}}_{\mathrm{k}}^{-1} \boldsymbol{x}(\mathrm{t}), \\ \quad \mathrm{k}_1, \mathrm{k}_2, \cdots, \mathrm{k}_{\mathrm{N}} \in\{1, 2, \cdots, \mathrm{M}\} \\ \hat{\boldsymbol{S}}_{\mathrm{j}}{ }^{(\mathrm{k})}(\mathrm{t})=0, \mathrm{j} \in\{1, 2, \cdots, \mathrm{N}\}, \\ \quad\mathrm{j} \neq \mathrm{k}_1, \mathrm{k}_2, \cdots, \mathrm{k}_{\mathrm{N}}\end{array}\right.$ | (22) |
3) 计算式(22)
| $\mathrm{J}_{\mathrm{k}}=\sum\limits_{\mathrm{i}=1}^{\mathrm{N}}\left|\hat{\boldsymbol{S}}^{(\mathrm{k})}(\mathrm{t})\right|^{\mathrm{p}}, \mathrm{k}=1, 2, \cdots, \mathrm{C}_{\mathrm{M}}^{\mathrm{N}}, \mathrm{p} \in(0, 1]$ | (23) |
4) 根据式(24)确定最小lp范数解
| $\hat{\boldsymbol{S}}(\mathrm{t})=\hat{\boldsymbol{S}}_{\min }(\mathrm{t})=\operatorname{argmin}_{\mathrm{k}}, \mathrm{k}=1, 2, \cdots, \mathrm{C}_{\mathrm{M}}^{\mathrm{N}}$ | (24) |
5) 重复步骤2~4,直至求出所有时刻的
为了衡量算法重构出的音频质量,本研究引入相似系数、信噪比和均方误差。
相似系数ξij以分离输出信号yi与源信号sj的相似系数作为盲源分离性能的度量。其计算公式为:
| $\xi_{\mathrm{ij}}=\xi\left(\boldsymbol{y}_{\mathrm{i}}, \boldsymbol{s}_{\mathrm{j}}\right)=\frac{\left|\sum\limits_{\mathrm{t}=1}^{\mathrm{T}} \boldsymbol{y}_{\mathrm{i}}(\mathrm{t}) \boldsymbol{s}_{\mathrm{j}}(\mathrm{t})\right|}{\sqrt{\sum\limits_{\mathrm{t}=1}^{\mathrm{T}} \boldsymbol{y}_{\mathrm{i}}{ }^2(\mathrm{t}) \sum\limits_{\mathrm{t}=1}^{\mathrm{T}} \boldsymbol{s}_{\mathrm{j}}{ }^2(\mathrm{t})}}$ | (25) |
式中,ξij取值范围为[0, 1], 当ξij=1时,说明第i个分离信号与第j个源信号的波形完全相同,当ξij=0时,yi与sj相互独立,ξij的取值越大,说明两者越相似。
信噪比是指系统中信号与噪声的比例,本研究使用信噪比来描述重构信号较源信号失真的程度,其计算公式为:
| $\mathrm{SNR}_{\mathrm{j}}=10 \log _{10}\left\{\frac{\sum\limits_{\mathrm{t}} \boldsymbol{s}_{\mathrm{j}}{ }^2(\mathrm{t})}{\sum\limits_{\mathrm{t}}\left[\boldsymbol{y}_{\mathrm{i}}(\mathrm{t})-\boldsymbol{s}_{\mathrm{j}}(\mathrm{t})\right]^2}\right.$ | (26) |
SNR的值越高表示效果越好。
均方误差是预测数据和原始数据对应点误差的平方和的均值,其计算公式为:
| $\operatorname{MSE}=\frac{1}{\mathrm{n}} \sum\limits_{\mathrm{i}=1}^{\mathrm{n}}\left(\boldsymbol{y}_{\mathrm{i}}-\boldsymbol{s}_{\mathrm{j}}\right)^2$ | (27) |
MSE的值说明了源信号与重构信号的差异性,其值越小表示效果越好。
2 结果 2.1 3源2观下不同时长生猪音频信号的欠定盲源分离图 2展示了12~16 s不等长的不同生猪状态下的音频信号波形图,采用补零方式将不同长度的音频对齐,运用幅值衰减矩阵A(式(28))将图 2展示的生猪哼叫声、呼噜声、咆哮声进行融合,得到音频观测信号波形如图 3所示。在统一采样率44.1 kHz的前提下,设置不同采样点数来获取5、9、12 s的生猪观测音频。由于试验的一般过程大同小异,只在最终重构的结果上有所差异,因此本研究以在12 s生猪观测信号下完成的欠定生猪盲源信号分离过程为例,来阐述单源点以及混合矩阵估计的部分,图 3~7和表 1均为在12 s观测音频前提下得到的试验结果。

|
图 2 不同状态下的生猪原始音频信号波形图 Fig. 2 Original audio signal waveform of pigs in different states |

|
图 3 生猪观测音频信号波形图 Fig. 3 Waveform of pig observed audio signal |
|
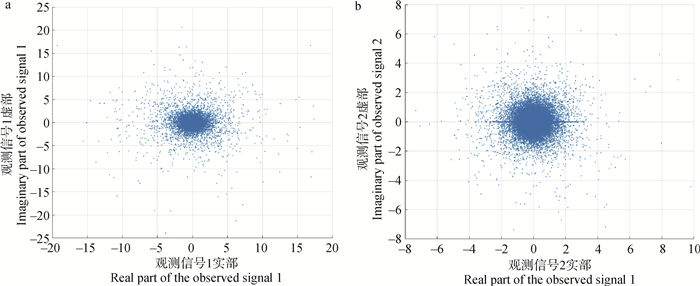
a.观测信号1;b.观测信号2 a.Observed signal 1;b.Observed signal 2 图 4 时频域下时长12 s的观测信号散点图 Fig. 4 Scatter plots of observed signals with a duration of 12 s in time-frequency domain |
|
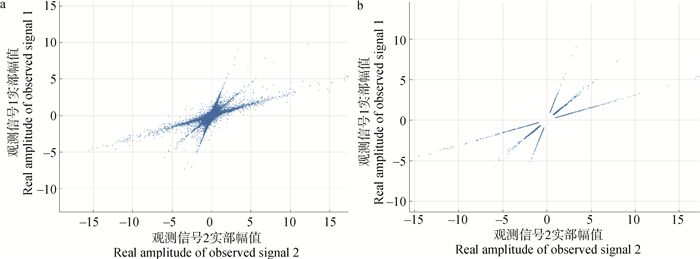
a.观测信号;b.单源点 a.Observed signal; b.Single source points 图 5 时频域下时长12 s的观测信号和提取到的单源点实部散点图 Fig. 5 Scatter plots of the real part of observed signal and extracted single source point with a duration of 12 s in the time-frequency domain |
|
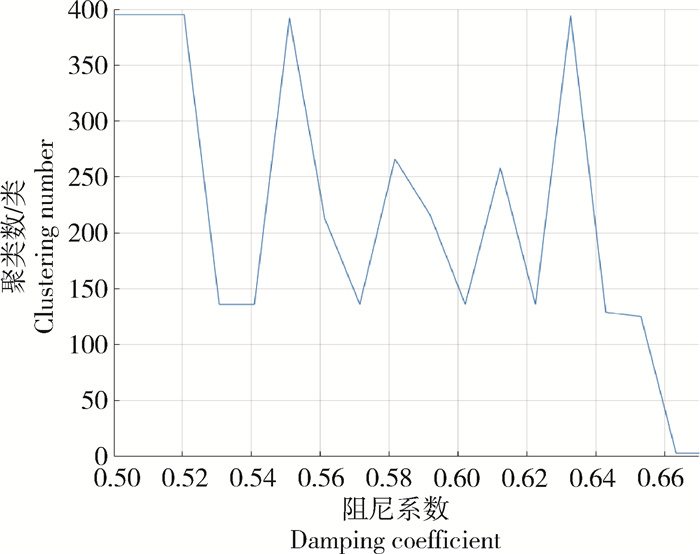
图 6 不同阻尼系数及聚类结果 Fig. 6 Different damping coefficients and clustering results |
|
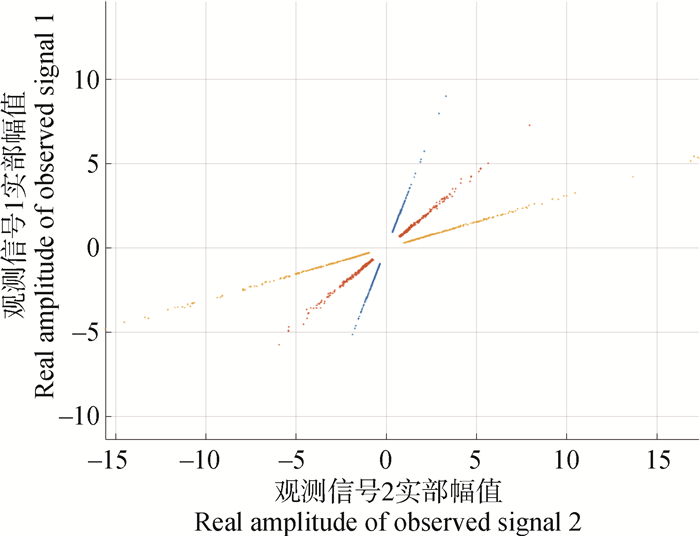
图 7 改进AP聚类结果 Fig. 7 Clustering results of improved AP |
|
|
表 1 聚类结果迭代次数和轮廓系数对比 Table 1 Comparison of iteration times and silhouette coefficients of clustering results |
对观测信号做短时傅里叶变换,选择汉宁窗为窗函数,窗大小设置为512,窗重叠为256,得到两个观测信号的复数矩阵,图 4展示了观测信号做STFT后的复数矩阵可视化散点图。根据“1.4”节所提方法,设置M=6,ε1=0.01,ε2=0.05,σ=0.5,提取单源点。图 5为观测信号在提取单源点前后的实部对比散点图,可以直观的看出,经过本研究所提方法进行单源点筛选后,信号的幅值在二维平面上清晰地呈3条直线分布,且低能点基本剔除。
采用改进的AP聚类算法对提取的特征单源点进行聚类,试验时设置最大迭代次数为500,迭代终止次数为50,使用自适应法则对阻尼系数进行调整,设置窗长度L为6,初始阻尼系数λ为0.5,记录每次阻尼系数调整前的最终聚类数,图 6表明聚类时阻尼系数以及聚类结果的变化曲线,随着迭代次数的逐渐增加,当λ初始值为0.5时,聚类结果较大,数值振荡,随着阻尼系数的不断增大,聚类数目也在不断变化,当λ的值增大到0.67时,聚类个数趋于稳定。表 1展示了AP与SVD-AP在迭代次数和轮廓系数上的结果,可以看到,SVD-AP迭代次数小于AP算法,且轮廓系数略大。图 7示出了改进AP算法对于观测信号的实部聚类结果,可以清晰地看到呈一条直线状的特征点聚为一类,总共聚为3类,分别用不同颜色表示。
| $\boldsymbol{A}=\left[\begin{array}{lll}0.955 & 0.366 & 0.621 \\ 0.296 & 0.997 & 0.555\end{array}\right]$ | (28) |
按照“1.6”中的方法从混合音频中分离音频信号,表 2表明在观测信号为12 s的前提下,不同p值重构出的音频信号与源信号的平均信噪比,根据p值的不同,平均信噪比的值在7.3~9.1 dB之间变化,当p值选取为0.8时,分离出的波形最优,平均信噪比值最大,因此这里选取p为0.8来完成音频的重构。
|
|
表 2 不同p值下源信号与重构信号的平均信噪比 Table 2 Average signal-to-noise ratio of the source signals and the reconstructed signals at different p-values |
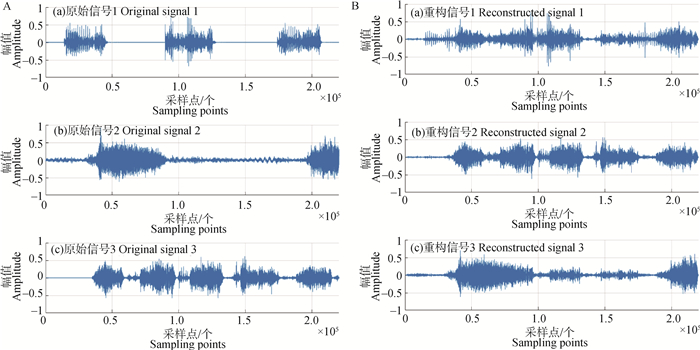
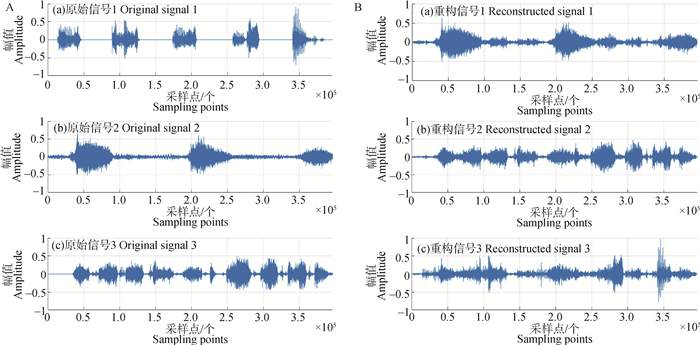
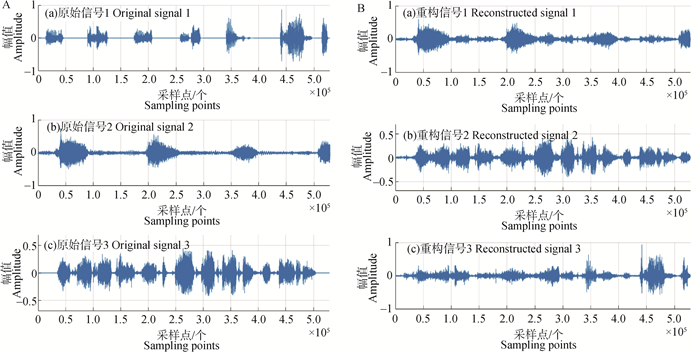
图 8~10展示了观测信号时长为5、9、12 s下的生猪音频源信号和重构信号的波形,重构后的音频排列顺序与源信号输入顺序并不一致,文献[36]采用按频率聚类解决排序二义性问题,然而本研究的重点在于“两步法”的欠定生猪音频信号的盲源分离,因此这里对于排序问题不加讨论;从波形上看,不同时长下的源信号2、3与对应的重构信号大致一样,幅值大小有略微差别,不同之处主要在于无效音频(噪声)段,不同时长下的源信号1与对应的重构信号有较明显的区别,对比源信号与重构信号可知,重构信号在源信号波形的基础上增加了其他许多波段,可能是由于源信号1的静音段较多,在与其他音频混合后,各静音段特征不再明显,受到其他源信号的影响较大,使得最终结果上有所差异;整体上看,观测信号为5、9、12 s在相同采样点部分的分离效果基本一致,且算法不受时间长度影响,较为稳定。为了衡量重构音频质量,测得不同时长下的源信号与对应观测信号的相似系数、信噪比和均方误差(表 3),从局部上看,不同时长下的重构信号1与对应源信号的相似系数在0.67~0.76之间,数值较低,信噪比在7.9~8.2 dB之间,均方误差在0.006~0.015之间;不同时长下的重构信号2和3与对应源信号的相似系数在0.88~0.92和0.90~0.93之间,信噪比在9.2~9.5 dB和9.4~9.7 dB之间,均方误差在0.005~0.08和0.008~0.03之间。从整体上看,分离信号与源信号的相似系数、信噪比和均方误差分别在0.67~0.92、7.9~9.7 dB和0.005~0.08之间,各测量值结果不同可能与不同采样点数、其他源信号干扰、信号本身在某个时间段特征凸显较弱和幅值一定程度的衰减有关。将分离后的信号写成wav文件,经主观试听和比较,发现略有杂音,整体效果良好。
|
A.源信号;B.重构信号 A.Source audio signals; B.Reconstructed audio signals 图 8 5 s生猪观测信号下的重构音频波形图 Fig. 8 Reconstructed audio waveform of pig observed signals at 5 s |
|
A.源信号;B.重构信号 A.Source audio signal; B.Reconstructed audio signal 图 9 9 s生猪观测信号下的重构音频波形图 Fig. 9 Reconstructed audio waveform of pig observed signals at 9 s |
|
A.源信号;B.重构信号 A.Source audio signal; B.Reconstructed audio signal 图 10 12 s生猪观测信号下的重构音频波形图 Fig. 10 Reconstructed audio waveform of pig observed signals at 12 s |
|
|
表 3 音频源信号与重构信号指标 Table 3 Indicators of audio source signals and reconstructed signals |
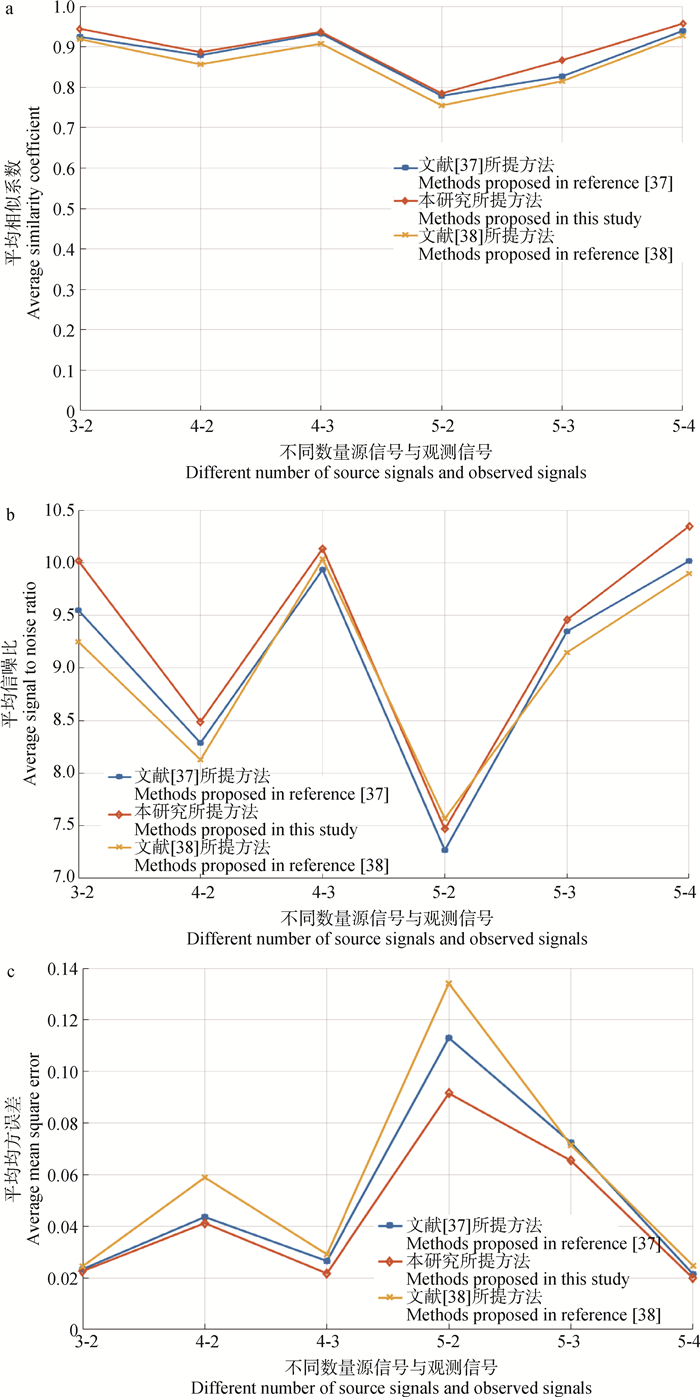
为了衡量算法的性能,本研究另选取15 s左右的生猪哼叫声、呼噜声、咆哮声、进食声和尖叫声音频信号,分别设置3×2、4×2、4×3、5×2、5×3、5×4数值不同的幅值衰减矩阵,构造小于源信号数的不同数量的观测信号,进行欠定生猪盲源信号分离,并与文献[37]、[38]方法做对比,将测量指标结果展示如图 11,其中x轴坐标数字为“源信号数-观测信号数”,y轴显示的数值为所有分离信号与源信号测得的对应评价指标的平均值。
|
a.平均相似系数;b.平均信噪比;c.平均均方误差 a.Average similarity coefficient; b.Average signal to noise ratio; c.Average mean square error 图 11 不同数量源信号和观测信号下的重构指标 Fig. 11 Reconstruction indexes under different number of source signals and observed signals |
从图 11可知,对于不同数量的源信号与观测信号,分离出来的音频质量指标各不相同,在源信号数一定时,观测信号数越多,各方法测得的质量指标越好,分离出来的音频越可靠。在相似系数上,文献[37]与[38]分别在0.778~0.939和0.755~0.927,本研究所提方法测得的数值在0.785~0.957;在信噪比上,文献[37]与[38]分别在7.268~10.017 dB和7.568~9.897 dB,本研究所提方法测得的数值在7.468~10.347 dB;在平均均方误差上,文献[37]与[38]分别在0.021~0.113和0.025~0.135,而本研究所提方法数值在0.019~0.092;从整体上看,本研究所提方法所测的平均相似系数、平均信噪比的值较高,平均均方误差的值较低,优于文献[38]所述方法,略微好于文献[37]所提方法。
3 讨论猪肉是我国主要的肉食来源,生猪的健康至关重要,在猪只生命周期中,其声音往往会反映所处的状态及行为,通过现代计算机技术对猪场音频的实时监测和识别,有助于养殖人员及时获取生猪信息,捕获异常。本研究针对生猪音频在识别过程中特征难以提取的问题,提出一种基于稀疏化理论的欠定生猪盲源信号分离方法,结果表明,该方法能够较为有效地分离出混合猪声信号的各源信号分量。
本研究将欠定盲源分离试验分为2步:混合矩阵估计和音频信号重构。混合矩阵估计包括单源点的提取和自适应SVD-AP聚类算法。本研究使用的单源点特征利用了音频信号的稀疏性,在一般单源点提取步骤的基础上,进行分组,计算每组的方差来进一步筛选,并且通过去除低能点来减少噪声误差,结果表明,该方法在使得聚类前的散点分布更为清晰,干扰点大多被剔除。AP聚类算法能获取单源点的类别数和各聚类结果,以此得到混合矩阵,本研究通过降维和自适应法则调参,证实了聚类算法估计混和矩阵的有效性,结果表明,该方法在迭代次数上有所减少,在轮廓系数上稍高,整体聚类效果良好。同时基于信号的稀疏性,采用最小lp范数进行重构音频信号,结果表明,不同的p值对于重构的音频质量有所影响,通过比较不同p值下分离音频信号的测量指标,选取最优值能够获取最大质量的音频重构信号。
本研究所用方法的好坏以其最终分离的音频质量和本身的稳定性来衡量,为此对5、9、12 s具有相同部分的不同时长的生猪音频进行试验,研究结果证实了本研究方法对于生猪欠定盲源分离的可行性,但该方法对于源信号中的静音段重构有一定误差。经比对其他方法发现,重构的音频在平均相似系数和信噪比较高,平均均方误差较低,整体情况较优,重构出的波形和计算的评价指标不受试验次数影响,具有一定的稳定性。
然而本研究尚存在一些局限性,在未来的研究中需要注意:1) 本研究为了便于衡量分离音频的质量,通过人工设置混合矩阵获得的观测信号,但在实际环境,并没有单一的源信号作为参考信号,对于通过算法分离音频信号以及在预处理时经过滤波降噪后的音频信号的质量如何评价还需进一步思考研究。2)本研究没有考虑源信号数如何确定,但在实际环境中,猪圈中采集到的音频由几头猪共同发出是未知的(即源信号数未知),有研究表明势函数[39]和盖氏圆的信源数估计法[40]可以作为源信号数的判断方法,后续可以结合相关理论,进一步研究源信号数的获取方式。3)在实际养殖环境中,猪舍的四周往往砌有墙壁,猪声的反射会对音频的盲源分离和识别带来一定的影响,有研究表明全局脉冲响应网络[41-42]能够降低混响声音对于盲源分离的影响,在后续研究中,可以通过模拟试验来测试该网络的效果。
4 结论本研究提出了一种基于稀疏化理论的欠定生猪盲源信号分离方法,通过调整聚类、重构参数发现,生猪音频的几种源信号在混合后经过本研究所提方法能够较为有效的分离,另外通过多次试验和对比,本研究方法具有一定的稳定性,在评价指标上有较优的表现,研究结果为实际环境中混合生猪音频的特征提取奠定了基础,对于猪场生猪音频的识别与监测具有一定的参考价值。
| [1] |
冯泽猛, 张云华, 贺玉敏, 等. 智能养殖: 生猪行为研究及其应用[J]. 农业现代化研究, 2021, 42(1): 1-9. FENG Z M, ZHANG Y H, HE Y M, et al. Intelligent breeding: the research and application of pig behavior[J]. Research of Agricultural Modernization, 2021, 42(1): 1-9. (in Chinese) |
| [2] |
刘铃, 王丹丹, 崔凯, 等. 猪繁殖与呼吸综合征抗病育种研究进展[J]. 畜牧兽医学报, 2023, 54(2): 434-442. LIU L, WANG D D, CUI K, et al. Advances of disease-resistant breeding on porcine reproductive and respiratory syndrome[J]. Acta Veterinaria et Zootechnica Sinica, 2023, 54(2): 434-442. (in Chinese) |
| [3] |
刘龙申, 舒翠霓, 李波, 等. 基于EfficientDet的围产期母猪姿态识别[J]. 农业机械学报, 2022, 53(4): 271-279. LIU L S, SHU C N, LI B, et al. Recognition of perinatal sows' posture based on EfficientDet algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(4): 271-279. (in Chinese) |
| [4] |
沈明霞, 太猛, CEDRIC O, 等. 基于深层卷积神经网络的初生仔猪目标实时检测方法[J]. 农业机械学报, 2019, 50(8): 270-279. SHEN M X, TAI M, CEDRIC O, et al. Real-time detection method of newborn piglets based on deep convolution neural network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(8): 270-279. (in Chinese) |
| [5] |
邱洪涛. 基于深度学习与证据理论的多源生猪呼吸道疾病识别研究[D]. 合肥: 安徽农业大学, 2019. QIU H T. Recognition of respiratory diseases in pigs with multiple sources based on deep learning and evidence theory[D]. Hefei: Anhui Agricultural University, 2019. (in Chinese) |
| [6] |
CHA C N, PARK E K, YOO C Y, et al. Changes in the appetite and behavior of cattle and pigs inoculated with the foot-and-mouth disease vaccine[J]. J Prev Vet Med, 2016, 40(4): 166-168. DOI:10.13041/jpvm.2016.40.4.166 |
| [7] |
刘振宇, 赫晓燕, 桑静, 等. 基于隐马尔可夫模型的猪咳嗽声音识别的研究[C]//中国畜牧兽医学会. 中国畜牧兽医学会信息技术分会第十届学术研讨会论文集. 北京: 中国农业大学出版社, 2015: 107-112. LIU Z Y, HE X Y, SANG J, et al. Research on pig cough sound recognition based on hidden Markov model[C]//Chinese Association of Animal Science and Veterinary Medicine. Proceedings of the 10th Symposium of Information Technology Branch of Chinese Society of Animal Husbandry and Veterinary Medicine. Beijing: China Agricultural University Press, 2015: 107-112. (in Chinese) |
| [8] |
ZHAO J, LI X, LIU W H, et al. DNN-HMM based acoustic model for continuous pig cough sound recognition[J]. Int J Agric Biol Eng, 2020, 13(3): 186-193. |
| [9] |
吴亚文. 基于音频压缩传输与端点检测的生猪音频识别研究[D]. 合肥: 安徽农业大学, 2021. WU Y W. Research on pig audio recognition based on audio compression transmission and endpoint detection[D]. Hefei: Anhui Agricultural University, 2021. (in Chinese) |
| [10] |
彭硕, 刘东阳, 时国龙, 等. 基于深度神经网络及隐马尔科夫模型的生猪状态音频识别[J]. 中国农业大学学报, 2022, 27(6): 172-181. PENG S, LIU D Y, SHI G L, et al. Pig state audio recognition based on deep neural network and hidden Markov model[J]. Journal of China Agricultural University, 2022, 27(6): 172-181. (in Chinese) |
| [11] |
CORDEIRO A F D S, NÄÄS I D A, DA SILVA LEITÃO F, et al. Use of vocalisation to identify sex, age, and distress in pig production[J]. Biosyst Eng, 2018, 173: 57-63. DOI:10.1016/j.biosystemseng.2018.03.007 |
| [12] |
冷碧滨, 吉雪强, 曾颢, 等. 中国大规模生猪养殖技术效率研究[J]. 浙江农业学报, 2018, 30(6): 1082-1088. LENG B B, JI X Q, ZENG H, et al. Study on technical efficiency of large-scale pig breeding in China[J]. Acta Agriculturae Zhejiangensis, 2018, 30(6): 1082-1088. (in Chinese) |
| [13] |
YANG Z Y, ZHOU G X, XIE S L, et al. Blind spectral unmixing based on sparse nonnegative matrix factorization[J]. IEEE Trans Image Process, 2010, 20(4): 1112-1125. |
| [14] |
ZHOU G X, ZHAO Q B, ZHANG Y, et al. Linked component analysis from matrices to high-order tensors: applications to biomedical data[J]. Proc IEEE, 2016, 104(2): 310-331. DOI:10.1109/JPROC.2015.2474704 |
| [15] |
JUN H, CHEN Y, ZHANG Q H, et al. Blind source separation method for bearing vibration signals[J]. IEEE Access, 2018, 6: 658-664. DOI:10.1109/ACCESS.2017.2773665 |
| [16] |
GEORGIEV P, THEIS F, CICHOCKI A. Sparse component analysis and blind source separation of underdetermined mixtures[J]. IEEE Trans Neural Netw, 2005, 16(4): 992-996. DOI:10.1109/TNN.2005.849840 |
| [17] |
GUO Q, RUAN G Q, LIAO Y P. A time-frequency domain underdetermined blind source separation algorithm for MIMO radar signals[J]. Symmetry, 2017, 9(7): 104. |
| [18] |
CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Rev, 2001, 43(1): 129-159. |
| [19] |
BOFILL P, ZIBULEVSKY M. Underdetermined blind source separation using sparse representations[J]. Signal Process, 2001, 81(11): 2353-2362. |
| [20] |
GEORGIEV P G, THEIS F, CICHOCKI A. Optimization algorithms for sparse representations and applications[M]//HAGER W W, HUANG S J, PARDALOS P M, et al. Multiscale Optimization Methods and Applications. New York: Springer, 2006: 85-99.
|
| [21] |
ZHEN L L, PENG D Z, YI Z, et al. Underdetermined blind source separation using sparse coding[J]. IEEE Trans Neural Netw Learn Syst, 2017, 28(12): 3102-3108. |
| [22] |
JOURJINE A, RICKARD S, YILMAZ O. Blind separation of disjoint orthogonal signals: demixing N sources from 2 mixtures[C]//2000 IEEE International Conference on Acoustics, Speech, and Signal Processing. Istanbul: IEEE, 2000: 2985-2988.
|
| [23] |
XIE Y, XIE K, XIE S L. Underdetermined blind separation of source using lp-norm diversity measures[J]. Neurocomputing, 2020, 411: 259-267. |
| [24] |
ARBERET S, GRIBONVAL R, BIMBOT F. A robust method to count and locate audio sources in a multichannel underdetermined mixture[J]. IEEE Trans Signal Process, 2010, 58(1): 121-133. |
| [25] |
HASSAN N, RAMLI D A. Sparse component analysis (SCA) based on adaptive time—frequency thresholding for underdetermined blind source separation (UBSS)[J]. Sensors, 2023, 23(4): 2060. |
| [26] |
于和新. 欠定盲源分离的预估分离两步法[D]. 大连: 大连理工大学, 2021. YU H X. Two-stages predictive and separation method for underdetermined blind source separation[D]. Dalian: Dalian University of Technology, 2021. (in Chinese) |
| [27] |
LI Y Q, CICHOCKI A, AMARI S I. Analysis of sparse representation and blind source separation[J]. Neural Comput, 2004, 16(6): 1193-1234. |
| [28] |
高鹰, 谢胜利, 许若宁, 等. 基于粒子群优化算法的稀疏信号盲分离[J]. 系统仿真学报, 2006, 18(8): 2264-2266. GAO Y, XIE S L, XU R N, et al. Blind sparse source separation based on particle swarm optimization[J]. Journal of System Simulation, 2006, 18(8): 2264-2266. (in Chinese) |
| [29] |
田旭, 马晓川, 封超, 等. 基于稀疏分量分析的振动信号源识别方法[J]. 信号处理, 2021, 37(6): 1034-1045. TIAN X, MA X C, FENG C, et al. Vibration signal sources identification method based on sparse component analysis[J]. Journal of Signal Processing, 2021, 37(6): 1034-1045. (in Chinese) |
| [30] |
FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976. |
| [31] |
DUAN Y X, LIU C Y, LI S, et al. An automatic affinity propagation clustering based on improved equilibrium optimizer and t-SNE for high-dimensional data[J]. Inf Sci, 2023, 623: 434-454. |
| [32] |
王开军, 张军英, 李丹, 等. 自适应仿射传播聚类[J]. 自动化学报, 2007, 33(12): 1242-1246. WANG K J, ZHANG J Y, LI D, et al. Adaptive affinity propagation clustering[J]. Acta Automatica Sinica, 2007, 33(12): 1242-1246. (in Chinese) |
| [33] |
CHARTRAND R, YIN W T. Iteratively reweighted algorithms for compressive sensing[C]//2008 IEEE International Conference on Acoustics, Speech and Signal Processing. Las Vegas: IEEE, 2008: 3869-3872.
|
| [34] |
SAAB R, YILMAZ O, MCKEOWN M J, et al. Underdetermined anechoic blind source separation via lq-basis-pursuit with q≪1[J]. IEEE Trans Signal Process, 2007, 55(8): 4004-4017. |
| [35] |
YANG J J, GUO Y, YANG Z Y, et al. Under-determined convolutive blind source separation combining density-based clustering and sparse reconstruction in time-frequency domain[J]. IEEE Trans Circuits Syst Ⅰ Regul Pap, 2019, 66(8): 3015-3027. |
| [36] |
SAWADA H, ARAKI S, MAKINO S. Underdetermined convolutive blind source separation via frequency bin-wise clustering and permutation alignment[J]. IEEE Trans Audio Speech Lang Process, 2011, 19(3): 516-527. |
| [37] |
HE X S, HE F, CAI W H. Underdetermined BSS based on K-means and AP clustering[J]. Circuits Syst Signal Process, 2016, 35(8): 2881-2913. |
| [38] |
季策, 姜雨田. 基于方向幅值比的欠定盲源分离算法[J]. 东北大学学报: 自然科学版, 2019, 40(7): 920-924. JI C, JIANG Y T. Underdetermined blind source separation algorithm based on directional amplitude ratio[J]. Journal of Northeastern University: Natural Science, 2019, 40(7): 920-924. (in Chinese) |
| [39] |
马宝泽, 张天骐, 安泽亮, 等. 一种多维信源衰减延时混合的欠定盲源分离方法[J]. 电子与信息学报, 2021, 43(8): 2258-2266. MA B Z, ZHANG T Q, AN Z L, et al. An underdetermined blind source separation approach for attenuated and time-delayed mixtures of multiple sources[J]. Journal of Electronics & Information Technology, 2021, 43(8): 2258-2266. (in Chinese) |
| [40] |
马宝泽. 基于瞬时和卷积混合模型的盲信号分离方法研究[D]. 重庆: 重庆邮电大学, 2021. MA B Z. A dissertation submitted to chongqing university of posts and telecommunications in partial fulfillment of the requirement for the degree of doctor of engineering[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2021. (in Chinese) |
| [41] |
解元, 邹涛, 孙为军, 等. 面向高混响环境的欠定卷积盲源分离算法[J]. 通信学报, 2023, 44(2): 82-93. XIE Y, ZOU T, SUN W J, et al. Algorithm of underdetermined convolutive blind source separation for high reverberation environment[J]. Journal on Communications, 2023, 44(2): 82-93. (in Chinese) |
| [42] |
解元, 邹涛, 孙为军, 等. 面向卷积混叠环境下的盲源分离新方法[J/OL]. 自动化学报, 2023, doi: 10.16383/j.aas.c211207. XIE Y, ZOU T, SUN W J, et al. Novel blind source separation method for convolutive mixed environment[J/OL]. Acta Automatica Sinica, 2023, doi: 10.16383/j.aas.c211207.(inChinese) |
(编辑 郭云雁)



