产蛋性状是肉种鸡重要的经济性状,产蛋数的提高不仅直接增加产雏数,同时增加投入产出比,是育种中必须持续稳定选育的指标之一。但产蛋数属于低遗传力性状,在肉用品系中由于种鸡体型大,传统的家系选择方法准确性低,急需应用新技术提高遗传进展。目前,利用基因组信息开展的产蛋性状基因组选择将有效提高选育准确性。
Henderson[1]于上世纪60年代提出了基于混合模型方程组的最佳线性无偏预测(best linear unbiased prediction, BLUP)模型,利用个体以及亲属信息构建亲缘关系矩阵。传统BLUP方法过度依赖于系谱和表型信息的记录准确性,因此受到环境和其他因素的影响较大。基因组选择技术在2001年被提出,其优势在于可以提高遗传评定的准确性,缩短世代间隔,对表型不易测量和低遗传力的性状选择具有较大的优势[2-4]。在褐壳蛋鸡中的研究发现,基于基因组选择的后代测定的16个性状,其性成熟年龄、产蛋量、产蛋率等都优于进行常规选择的群体[5]。在鸡的疾病抗性选择中也表现出相同的结果[6-7]。Yin等[8]于2020年提出了一种机器学习方法KAML方法(Kinship-adjusted-multiple-loci,KAML),其机器学习方法整合了交叉验证、二分法迭代等算法,可以将较大标记效应纳入到混合线性模型协变量中,并同时根据标记贡献赋予一定权重,从而提高估计准确性。
本研究的目的是比较不同算法基因组预测准确性,以白羽肉鸡产蛋数为研究重点,对遗传参数进行估计,并分析包括机器学习算法在内的7个模型对白羽肉种鸡产蛋性状的预测准确性。为在白羽肉鸡产蛋性状中实施基因组选择技术提供理论依据。
1 材料与方法 1.1 试验群体本研究使用的产蛋数和蛋重数据来源于弥勒新广农牧科技有限公司培育的快大型白羽肉鸡的一个品系,共选择了8个世代,本研究使用第6和7世代个体,共包含2 474个个体的系谱数据和基因型数据。其中包括公鸡697只,母鸡1 777只。每只鸡单笼饲养,每个笼位附有条形码。用条码扫描器产蛋记录系统记录鸡群每日产蛋数量,并标注畸形蛋和破蛋情况。统计43周龄、60周龄的合格蛋数、合格蛋率、总产蛋数等指标,其中只有第6世代有60周产蛋数。在52周龄连续测定1周个体蛋重,剔除称量蛋数少于3枚的蛋重,计算每个个体的平均蛋重。
1.2 基因分型、填充和质量控制在43周龄时翅下静脉采血,EDTA抗凝后-20 ℃保存用于基因组DNA提取,通过苯酚-氯仿法提取血样中的基因组DNA,利用“京芯一号” 55K SNP芯片[9]对2 474个个体进行基因型检测。基因分型后共得到44 561个SNPs,使用PLINK(V1.9)[10]软件对数据进行质量控制,质控条件设为保留最小等位基因≥5%、基因分型率≥90%的位点,个体分型率≥90%的个体。质控后使用Beagle 5.0软件[11]对缺失的SNP进行填充。最终保留个体2 474个,SNP位点个数是38 019个,保留个体和SNP用于后续研究。
1.3 基因组预测的统计模型分别利用KAML、PBLUP、GBLUP、SSGBLUP、Bayes A、Bayes B和Bayes Cπ 7种模型进行分析。其中KAML算法的模型介绍同文献[8],通过R软件包“KAML”进行计算。
Bayes方法使用R软件包“BGLR”进行计算,迭代次数设置为5 000次。
基于系谱(PBLUP)、基因型(GBLUP)和两者结合(SSGBLUP)的最佳线性无偏预测方法对有基因型和系谱的2 474只鸡的群体进行育种值估计。统计模型如下:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Xb}} + \mathit{\boldsymbol{Z\alpha }} + \mathit{\boldsymbol{e}} $ |
其中y是52周蛋重或43周产蛋数值的向量; X和Z是固定效应和加性遗传效应的关联矩阵,本研究将世代和批次作为固定效应加入到模型中; b是固定效应向量,α是随机加性遗传效应向量,e是随机残差向量,假设
| $ \boldsymbol{H}^{-1}=\boldsymbol{A}^{-1}+\left[\begin{array}{cc} 0 & 0 \\ 0 & G_{w}^{-1}-A_{w}^{-1} \end{array}\right] $ |
在逆矩阵中:
| $ \boldsymbol{G}_{\boldsymbol{w}}=(1-w) \boldsymbol{G}+w \boldsymbol{A}_{22} $ |
w为加权系数,VanRaden[12]将w=0.05作为构建H矩阵的默认参数,对G矩阵进行加权:Gw =0.95 G +0.05 A [13]。
本次试验估计的方差组分和预测的育种值基于ASReml v4.1软件[14]进行计算。遗传力和方差组分计算使用单性状模型,产蛋性状之间的相关性采用双性状模型进行估计。
1.4 不同算法基因组预测准确性比较对43周总产蛋数和52周蛋重两个性状进行不同算法基因组预测准确性的比较。
育种值预测准确性评估方式为交叉验证,育种值估计准确性用固定效应校正后的表型与估计育种值的pearson相关系数表示,秩相关用spearman相关系数表示。本研究利用5倍交叉验证进行评估,将有表型个体随机分为5组,其中4组为参考群,剩余1组为验证群,重复5次。为了获得更准确的结果,本研究进行了20次5倍交叉验证进行准确性评估。
SSGBLUP对于不同的群体和性状可能会有不同的w加权值,为了提高SSGBLUP对基因组育种值预测的准确性,需要首先调整w的参数确定对每个性状的最佳预测能力。
2 结果 2.1 群体数据的基本统计表型数据通过利用箱线图法剔除异常值,(Q1-1. 5*IQR)~(Q3+1. 5*IQR)以外的数值。式中:Q1指第一四分位数,Q3为第三四分位数; IQR为四分位距,指第三四分位数与第一四分位数的差值[15]。描述性统计见表 1。
|
|
表 1 产蛋性状描述性统计结果 Table 1 Descriptive statistics table of laying traits |
使用PBLUP、GBLUP、SSGBLUP三种模型估计6个性状的遗传力估计值见表 2。结果表明, GBLUP模型估计得到的遗传力略低于其他两个模型的估计值。4个产蛋数性状属于低遗传力性状,蛋重性状属于中等遗传力性状。
|
|
表 2 PBLUP、GBLUP和SSGBLUP方法估计产蛋性状的遗传力 Table 2 The heritability of egg laying traits was estimated by PBLUP, GBLUP and SSGBLUP methods |
产蛋性状之间的遗传相关性结果见表 3。产蛋数之间存在强的遗传正相关,蛋重与43周产蛋数存在中等的遗传负相关,与60周产蛋数存在中等偏低的遗传负相关。采用G矩阵和H矩阵估计的遗传相关与基于A矩阵估计的结果相似,未存在显著性差异。
|
|
表 3 产蛋性状之间的遗传相关性 Table 3 Genetic correlation between laying traits |
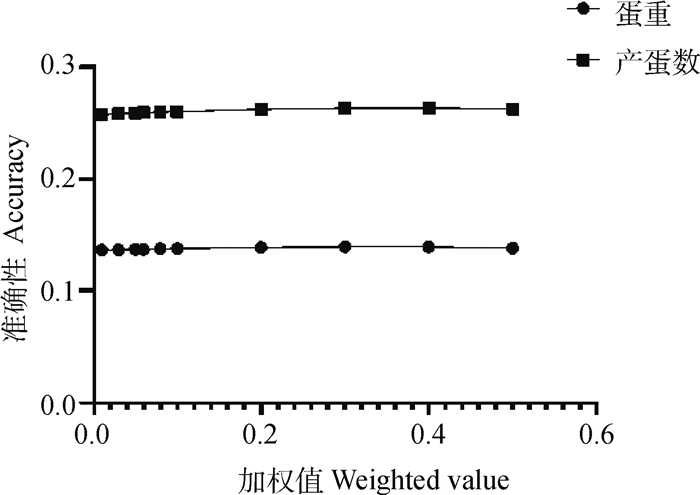
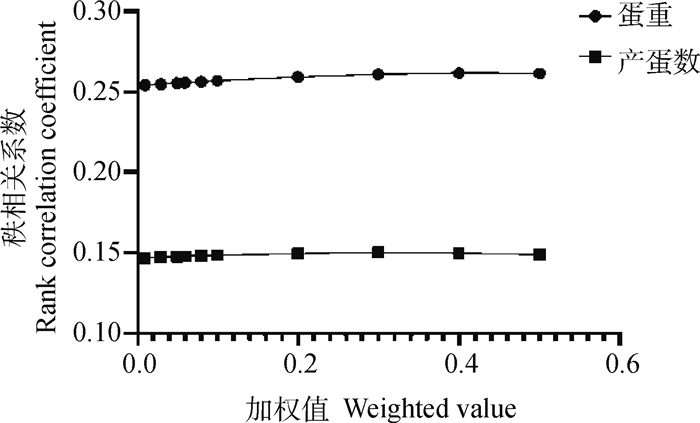
不同加权系数下SSGBLUP对43周产蛋数和52周蛋重的预测准确性和秩相关见图 1、2。当w=0.3时,对产蛋数和蛋重的基因组育种值估计的准确性和秩相关系数最高,当w=0.3时相较于默认值w=0.05时构建的H矩阵,预测准确性略有提升,但是提升幅度较小,因此下面计算依然以w=0.05为加权值。
|
图 1 不同w加权准确性比较 Fig. 1 Comparison of different w weighted accuracy |
|
图 2 不同w加权秩相关比较 Fig. 2 Comparison of different w weighted rank correlations |
本研究通过5倍交叉验证将育种值估计的准确性用表型与估计育种值的pearson相关系数表示。准确性结果和秩相关结果见表 4。1)使用基因组选择方法估计基因组育种值的准确性高于基于系谱信息预测的结果。Bayes方法相对于KAML方法和BLUP方法均有更高的准确性。2)KAML与GB- LUP估计育种值的准确性相似,Bayes A、Bayes B和Bayes Cπ的准确性接近。3)Bayes A方法对于蛋重有最高的准确性。4)Bayes Cπ对产蛋数有最高的准确性。
|
|
表 4 不同方法估计育种值的准确性和秩相关结果 Table 4 Accuracy and rank correlation comparison of different methods for estimating breeding value |
白羽肉鸡产业在畜牧业中贡献显著,其饲料转化率高,温室气体排放量低。鸡肉中蛋白质含量高,是一种环境友好、营养健康的肉类。产肉和产蛋是鸡产业的两大重要经济性状,由于肉鸡和蛋鸡在这两大经济性状中的选育方向不同,导致肉鸡在产蛋方面与蛋鸡相差甚远,因此肉鸡在产蛋性状中还有很大的选育空间[16]。
本研究采用系谱和基因组信息估计了白羽肉鸡品系产蛋性状遗传参数,产蛋数遗传力为0.061~0.16,属于低遗传力性状,蛋重的遗传力为0.28~0.39,属于中等偏高遗传力性状。本文PBLUP和SSGBLUP估计遗传力的结果与在洛岛红鸡报道的遗传力结果(蛋重遗传力0.22~0.36,产蛋数0.07~ 0.39)基本一致[17-18],但是GBLUP计算的遗传力相较于马赞达兰土鸡和洛岛红鸡的遗传力报道较低[18-19]。GBLUP估计得到的遗传力低于PBLUP和SSGBLUP估计的遗传力,该情况在鸡[20]、猪[21]和奶牛[22-23]报道中也有发现,可能的原因是:1)本研究用的基因组信息是55 K SNP芯片,并不能完全代表基因组,并且所用的模型只估计了加性遗传效应,导致估计出的加性遗传方差偏低[24-25]; 2)由于G矩阵没有定义基础群体,使得基因组遗传力估计值很可能偏低。A矩阵基于血缘一致性,根据系谱第一世代的公鸡和母鸡,合理地确定了一个定义基础群体。G矩阵基于状态一致性,缺乏系谱信息,使用研究群体作为基础群体[26]。Niknafs等[19]对伊朗本地品种鸡的研究表明,1、8和12周龄体重与产蛋数之间存在低的遗传负相关关系,因此前期体重与产蛋数有可能实现共同选育提高。本研究的相关性分析结果表明,60周产蛋数、合格蛋数和43周产蛋数、合格蛋数之间是强的正遗传相关关系,表明在选育的过程中提高43周产蛋数、合格蛋数的同时就可以提高60周产蛋数、合格蛋数。在蛋鸡中研究较多的有开产日龄、产蛋数、蛋重和开产体重之间的关系。本研究结果表明,蛋重和产蛋数之间是中等的遗传负相关(平均是-0.41)的关系。本研究只用了52周的蛋重,而在洛岛红鸡中有研究表明,28、36、56、66和72周的蛋重之间是强的遗传正相关,相关性在0.85以上[17]。有研究报道了开产体重与蛋重存在中等正相关的关系[19]; 开产日龄与产蛋数是较强的遗传负相关,开产日龄早的比开产晚的鸡倾向于产更多蛋,开产体重与产蛋数有中等负相关的关系[19, 27]。De Ketelaere等[28]报告称,蛋重较大可能会降低蛋壳厚度; 此外,蛋重与鸡蛋内部营养物质之间也有很强的遗传正相关[29]。因此,对蛋鸡产蛋数的选择要考虑蛋重的影响,过度选择产蛋数可能会导致蛋重减小,蛋重过小会影响孵化率和雏鸡质量[30]。相反,肉种鸡的体型较大,蛋重通常也较大,因此控制一定的蛋重对于提高产蛋数和保持蛋品质是必要的。
本研究重点比较了KAML、PBLUP、GBLUP、SSGBLUP、Bayes A、Bayes B和Bayes Cπ 7种方法对白羽肉鸡产蛋数和蛋重性状的育种值预测准确性。Bayes方法比KAML和BLUP方法有更高的准确性,这与Wu等[31]和Habier等[32]在奶牛群体和模拟数据中的研究结果一致。其原因是,与BLUP模型相比,Bayes模型更好地利用了SNP的连锁不平衡信息,并且更适合于标记密度增加的基因组预测以及参考群和候选群之间亲缘关系较远的情况[33-34]。3种Bayes模型计算出来的准确性较一致,它们之间的区别在于: 一是对每个SNP具有的效应假设不同,Bayes A假设每个SNP都具有效应,且效应不同; Bayes B假设只有一部分SNP具有效应,且效应不同; Bayes Cπ假设一部分SNP具有相同的效应。二是Bayes Cπ将SNP具有零影响的先验概率π视为未知,而Bayes A认为π=0,Bayes B认为π>0[8, 35]。计算效率是基因组选择与基因组预测在实际应用中的一个重要要求,这往往阻碍了Bayes方法的应用,导致BLUP模型成为基因组选择与基因组预测方法中应用最广泛的方法之一。
KAML方法与GBLUP和SSGBLUP方法估计育种值准确性相近,在Yin等[8]的报道中表明, KAML方法预测准确性显著高于GBLUP方法,与Bayes方法准确性相似,与本研究的结果不同。KAML方法提高预测准确性的方式是通过全基因组关联分析找到目标性状的显著相关位点,然后根据这些位点的贡献赋予更大权重后进行育种值估计。本研究使用的是55 K SNP芯片,并不能完全代表鸡的整个基因组,全基因组关联分析可能找不到准确的显著相关位点; 同时产蛋数和蛋重性状是由微效多基因控制,显著效应位点较少。
基因组选择中常用的BLUP方法有GBLUP和SSGBLUP,GBLUP是根据SNP标记信息构建的基因组关系矩阵,GBLUP假设的是基因组中的每个SNP均具有效应,且对总方差的效应是相等的[36]。由于GBLUP的计算要求所有个体具有基因型,而对于群体较大,个体价值小的经济动物,对全部个体基因分型成本较高,因此SSGBLUP方法的提出很快得到了应用。该方法将基于系谱关系构建的A矩阵与标记信息构建的G矩阵结合构成新的H矩阵[37-38]。通过两方面信息的整合可以使用更多的记录信息,减少基因分型成本,提高育种值估计的准确性。SSGBLUP受到芯片密度、群体系谱深度和完整性等因素的影响,不同群体、不同性状H矩阵的A矩阵和G矩阵加权系数可能会有不同影响,因此在使用SSGBLUP时检验H矩阵中两者的最佳权重是有必要的,本研究结果显示在本群体中调整权重对准确性有小幅度的提升,但是提升不显著,因此在实施SSGBLUP时依然以w=0.05为加权值是可行的。
育种值估计准确性表明,SSGBLUP预测产蛋数的准确性高于GBLUP和PBLUP,其原因在于SSGBLUP结合了系谱信息和基因组信息,相比于GBLUP,加入系谱信息可以补充SNP无法解释的遗传方差,可以提高预测的准确性[39-41]。本研究也表明,GBLUP的预测准确性高于PBLUP,可能的原因是PBLUP通过系谱估计亲缘关系是一个经验值,无法准确识别半同胞和全同胞个体之间的亲缘关系,得到的是一个期望的推断值,略差于基因组信息估计的亲缘关系。在其他物种中也表现出以上的结果,Habier等[32]报道,GBLUP对于育种值的估计相较于传统PBLUP方法更加准确。在猪中,基因组选择技术对生长速度、饲料转化率、产仔数、肉品质、抗病力等指标普遍具有较高的育种值估计准确性[42-45]。Yan等[46]对1 344只鸡进行基因分型,以28周体重、蛋重、产蛋量和哈氏单位4个性状为研究对象,发现SSGBLUP比基于系谱的PBLUP的准确性提高了16%。
4 结论本研究以白羽肉鸡作为研究群体,以产蛋性状为研究对象,通过PBLUP、GBLUP、SSGBLUP估计不同时期产蛋数和蛋重的遗传力与遗传相关,表明产蛋数性状是低遗传力性状,蛋重是中等遗传力性状,43周和60周产蛋数之间是强的遗传正相关的关系,产蛋数与蛋重是中等遗传负相关关系。比较7种方法的育种值估计准确性表明,机器学习方法KAML与GBLUP方法的准确性相似; Bayes方法预测准确性高于KAML和BLUP方法; BLUP方法中SSGBLUP方法预测产蛋数性状准确性最高; GBLUP预测蛋重性状准确性最高。研究结果显示基因组选择显著优于传统的选择方法。
| [1] |
HENDERSON C R. Best linear unbiased estimation and prediction under a selection model[J]. Biometrics, 1975, 31(2): 423-447. DOI:10.2307/2529430 |
| [2] |
MEUWISSEN T H E, HAYES B J, GODDARD M E. Prediction of total genetic value using genome-wide dense marker maps[J]. Genetics, 2001, 157(4): 1819-1829. DOI:10.1093/genetics/157.4.1819 |
| [3] |
赵志达, 张莉. 基因组选择在绵羊育种中的应用[J]. 遗传, 2019, 41(4): 293-303. ZHAO Z D, ZHANG L. Applications of genome selection in sheep breeding[J]. Hereditas (Beijing), 2019, 41(4): 293-303. DOI:10.3760/cma.j.issn.1003-9406.2019.04.001 (in Chinese) |
| [4] |
WIGGANS G R, COLE J B, HUBBARD S M, et al. Genomic selection in dairy cattle: the USDA experience[J]. Annu Rev Anim Biosci, 2017, 5: 309-327. DOI:10.1146/annurev-animal-021815-111422 |
| [5] |
WOLC A, STRICKER C, ARANGO J, et al. Breeding value prediction for production traits in layer chickens using pedigree or genomic relationships in a reduced animal model[J]. Genet Sel Evol, 2011, 43(1): 5. DOI:10.1186/1297-9686-43-5 |
| [6] |
LIU T F, QU H, LUO C L, et al. Genomic selection for the improvement of antibody response to Newcastle disease and avian influenza virus in chickens[J]. PLoS One, 2014, 9(11): e112685. DOI:10.1371/journal.pone.0112685 |
| [7] |
WOLC A, DROBIK-CZWARNO W, FULTON J E, et al. Genomic prediction of avian influenza infection outcome in layer chickens[J]. Genet Sel Evol, 2018, 50(1): 21. DOI:10.1186/s12711-018-0393-y |
| [8] |
YIN L L, ZHANG H H, ZHOU X, et al. KAML: improving genomic prediction accuracy of complex traits using machine learning determined parameters[J]. Genome Biol, 2020, 21(1): 146. DOI:10.1186/s13059-020-02052-w |
| [9] |
LIU R R, XING S Y, WANG J, et al. A new chicken 55K SNP genotyping array[J]. BMC Genomics, 2019, 20(1): 410. DOI:10.1186/s12864-019-5736-8 |
| [10] |
PURCELL S, NEALE B, TODD-BROWN K, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses[J]. Am J Hum Genet, 2007, 81(3): 559-575. DOI:10.1086/519795 |
| [11] |
BROWNING S R, BROWNING B L. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering[J]. Am J Hum Genet, 2007, 81(5): 1084-1097. DOI:10.1086/521987 |
| [12] |
VANRADEN P M. Efficient methods to compute genomic predictions[J]. J Dairy Sci, 2008, 91(11): 4414-4423. DOI:10.3168/jds.2007-0980 |
| [13] |
MISZTAL I, AGUILAR I, LEGARRA A, et al. Choice of parameters for single-step genomic evaluation for type[J]. J Dairy Sci, 2010, 93(S1): 166. |
| [14] |
GILMOUR A R, THOMPSON R, CULLIS B R. Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models[J]. Biometrics, 1995, 51(4): 1440-1450. DOI:10.2307/2533274 |
| [15] |
梁小军, 高慧兰, 马吉锋, 等. 中国荷斯坦奶牛月龄和胎间距的回归分析[J]. 黑龙江畜牧兽医, 2018(10): 92-95, 240. LIANG X J, GAO H L, MA J F, et al. Regression analysis of monthly age and spacing of Chinese Holstein dairy cows[J]. Heilongjiang Animal Science and Veterinary Medicine, 2018(10): 92-95, 240. (in Chinese) |
| [16] |
BUZAŁA M, JANICKI B, CZARNECKI R. Consequences of different growth rates in broiler breeder and layer hens on embryogenesis, metabolism and metabolic rate: a review[J]. Poult Sci, 2015, 94(4): 728-733. DOI:10.3382/ps/pev015 |
| [17] |
LIU Z, SUN C J, YAN Y Y, et al. Genome-wide association analysis of age-dependent egg weights in chickens[J]. Front Genet, 2018, 9: 128. DOI:10.3389/fgene.2018.00128 |
| [18] |
LIU Z, YANG N, YAN Y Y, et al. Genome-wide association analysis of egg production performance in chickens across the whole laying period[J]. BMC Genetics, 2019, 20(1): 67. DOI:10.1186/s12863-019-0771-7 |
| [19] |
NIKNAFS S, NEJATI-JAVAREMI A, MEHRABANI-YEGANEH H, et al. Estimation of genetic parameters for body weight and egg production traits in Mazandaran native chicken[J]. Trop Anim Health Prod, 2012, 44(7): 1437-1443. DOI:10.1007/s11250-012-0084-6 |
| [20] |
LI W, ZHENG M Q, ZHAO G P, et al. Identification of QTL regions and candidate genes for growth and feed efficiency in broilers[J]. Genet Sel Evol, 2021, 53(1): 13. DOI:10.1186/s12711-021-00608-3 |
| [21] |
ALDRIDGE M N, VANDENPLAS J, BERGSMA R, et al. Variance estimates are similar using pedigree or genomic relationships with or without the use of metafounders or the algorithm for proven and young animals1[J]. J Anim Sci, 2020, 98(3): skaa019. DOI:10.1093/jas/skaa019 |
| [22] |
HARDER I, STAMER E, JUNGE W, et al. Estimation of genetic parameters and breeding values for feed intake and energy balance using pedigree relationships or single-step genomic evaluation in Holstein Friesian cows[J]. J Dairy Sci, 2020, 103(3): 2498-2513. DOI:10.3168/jds.2019-16855 |
| [23] |
BOHLOULI M, ALIJANI S, NADERI S, et al. Prediction accuracies and genetic parameters for test-day traits from genomic and pedigree-based random regression models with or without heat stress interactions[J]. J Dairy Sci, 2019, 102(1): 488-502. DOI:10.3168/jds.2018-15329 |
| [24] |
MOGHADDAR N, VAN DER WERF J H J. Genomic estimation of additive and dominance effects and impact of accounting for dominance on accuracy of genomic evaluation in sheep populations[J]. J Anim Breed Genet, 2017, 134(6): 453-462. DOI:10.1111/jbg.12287 |
| [25] |
ESFANDYARI H, BIJMA P, HENRYON M, et al. Genomic prediction of crossbred performance based on purebred Landrace and Yorkshire data using a dominance model[J]. Genet Sel Evol, 2016, 48(1): 40. DOI:10.1186/s12711-016-0220-2 |
| [26] |
LI W, ZHENG M, ZHAO G, et al. Identification of QTL regions and candidate genes for growth and feed efficiency in broilers[J]. Genet Sel Evol, 2008, 91(11): 4414-4423. |
| [27] |
BEGLI H E, WOOD B J, ABDALLA E A, et al. Genetic parameters for clutch and broodiness traits in turkeys (Meleagris Gallopavo) and their relationship with body weight and egg production[J]. Poult Sci, 2019, 98(12): 6263-6269. DOI:10.3382/ps/pez446 |
| [28] |
DE KETELAERE B, GOVAERTS T, COUCKE P, et al. Measuring the eggshell strength of 6 different genetic strains of laying hens: techniques and comparisons[J]. Br Poult Sci, 2002, 43(2): 238-244. DOI:10.1080/00071660120121454 |
| [29] |
SAVEGNAGO R P, CAETANO S L, RAMOS S B, et al. Estimates of genetic parameters, and cluster and principal components analyses of breeding values related to egg production traits in a White Leghorn population[J]. Poult Sci, 2011, 90(10): 2174-2188. DOI:10.3382/ps.2011-01474 |
| [30] |
康相涛, 宋素芳, 李明, 等. 蛋鸡种蛋蛋重对孵化率和雏鸡生长发育的影响[J]. 中国家禽, 2002, 24(15): 10-11, 13. KANG X T, SONG S F, LI M, et al. The effects of egg weights of breeding layers on hatchability and development of chicks[J]. China Poultry, 2002, 24(15): 10-11, 13. DOI:10.3969/j.issn.1004-6364.2002.15.003 (in Chinese) |
| [31] |
WU X, LUND M S, SUN D, et al. Impact of relationships between test and training animals and among training animals on reliability of genomic prediction[J]. J Anim Breed Genet, 2015, 132(5): 366-375. DOI:10.1111/jbg.12165 |
| [32] |
HABIER D, FERNANDO R L, DEKKERS J C M. The impact of genetic relationship information on genome-assisted breeding values[J]. Genetics, 2007, 177(4): 2389-2397. DOI:10.1534/genetics.107.081190 |
| [33] |
GAO H, SU G, JANSS L, et al. Model comparison on genomic predictions using high-density markers for different groups of bulls in the Nordic Holstein population[J]. J Dairy Sci, 2013, 96(7): 4678-4687. DOI:10.3168/jds.2012-6406 |
| [34] |
SU G, BRØNDUM R F, MA P, et al. Comparison of genomic predictions using medium-density (~54, 000) and high-density (~777, 000) single nucleotide polymorphism marker panels in Nordic Holstein and Red Dairy Cattle populations[J]. J Dairy Sci, 2012, 95(8): 4657-4665. DOI:10.3168/jds.2012-5379 |
| [35] |
HABIER D, FERNANDO R L, KIZILKAYA K, et al. Extension of the Bayesian alphabet for genomic selection[J]. BMC Bioinformatics, 2011, 12: 186. DOI:10.1186/1471-2105-12-186 |
| [36] |
CLARK S A, VAN DER WERF J. Genomic best linear unbiased prediction (gBLUP) for the estimation of genomic breeding values[M]//GONDRO C, VAN DER WERF J, HAYES B. Genome-Wide Association Studies and Genomic Prediction. Totowa: Humana Press, 2013: 321-330.
|
| [37] |
LEGARRA A, AGUILAR I, MISZTAL I. A relationship matrix including full pedigree and genomic information[J]. J Dairy Sci, 2009, 92(9): 4656-4663. DOI:10.3168/jds.2009-2061 |
| [38] |
DUDOIT S, VAN DER LAAN M J, POLLARD K S. Multiple testing.Part I.Single-step procedures for control of general type I error rates[J]. Stat Appl Genet Mol Biol, 2004, 3(1): Article13. |
| [39] |
SU G S, CHRISTENSEN O F, OSTERSEN T, et al. Estimating additive and non-additive genetic variances and predicting genetic merits using genome-wide dense single nucleotide polymorphism markers[J]. PLoS One, 2012, 7(9): e45293. DOI:10.1371/journal.pone.0045293 |
| [40] |
KUMAR S, MOLLOY C, MUÑOZ P, et al. Genome-enabled estimates of additive and nonadditive genetic variances and prediction of apple phenotypes across environments[J]. G3 (Bethesda), 2015, 5(12): 2711-2718. DOI:10.1534/g3.115.021105 |
| [41] |
BAI H, SUN Y, LIU N, et al. Genome-wide detection of CNVs associated with beak deformity in chickens using high-density 600K SNP arrays[J]. Anim Genet, 2018, 49(3): 226-236. DOI:10.1111/age.12652 |
| [42] |
TRIBOUT T, LARZUL C, PHOCAS F. Efficiency of genomic selection in a purebred pig male line[J]. J Anim Sci, 2012, 90(12): 4164-4176. DOI:10.2527/jas.2012-5107 |
| [43] |
FORNI S, AGUILAR I, MISZTAL I. Different genomic relationship matrices for single-step analysis using phenotypic, pedigree and genomic information[J]. Genet Sel Evol, 2011, 43(1): 1. DOI:10.1186/1297-9686-43-1 |
| [44] |
LILLEHAMMER M, MEUWISSEN T H E, SONESSON A K. Genomic selection for two traits in a maternal pig breeding scheme[J]. J Anim Sci, 2013, 91(7): 3079-3087. DOI:10.2527/jas.2012-5113 |
| [45] |
GUO X, CHRISTENSEN O F, OSTERSEN T, et al. Improving genetic evaluation of litter size and piglet mortality for both genotyped and nongenotyped individuals using a single-step method[J]. J Anim Sci, 2015, 93(2): 503-512. DOI:10.2527/jas.2014-8331 |
| [46] |
YAN Y Y, WU G Q, LIU A Q, et al. Genomic prediction in a nuclear population of layers using single-step models[J]. Poult Sci, 2018, 97(2): 397-402. DOI:10.3382/ps/pex320 |
(编辑 范子娟)



