畜牧兽医学报  2022, Vol. 53 Issue (10): 3448-3458. DOI: 10.11843/j.issn.0366-6964.2022.10.017    PDF    
引用本文
张鹏飞, 何俊, 王立贤, 赵福平. 基于基因组和系谱信息的不同选配方案效果模拟研究[J]. 畜牧兽医学报, 2022, 53(10): 3448-3458.  
ZHANG Pengfei, HE Jun, WANG Lixian, ZHAO Fuping. Simulation Study on the Effects of Different Mating Schemes Based on Genomic and Pedigree Information[J]. Acta Veterinaria et Zootechnica Sinica, 2022, 53(10): 3448-3458.  
基于基因组和系谱信息的不同选配方案效果模拟研究
张鹏飞1, 何俊2, 王立贤1, 赵福平1     
1. 中国农业科学院北京畜牧兽医研究所 农业部动物遗传育种与繁殖(家禽)重点实验室，北京 100193;
2. 湖南农业大学动物科技学院，长沙 410128
收稿日期：2022-02-23
基金项目：国家自然科学基金面上项目(32172702)
作者简介：张鹏飞(1996-)，男，山东威海人，硕士生，主要从事动物遗传育种研究，E-mail: zhangpengfei3236@163.com.
通信作者：王立贤，主要从事猪遗传育种研究，E-mail: wlxians@263.net; 赵福平，主要从事统计基因组学和猪遗传育种研究，E-mail: zhaofuping@caas.cn.
摘要：基因组选配(genomic mating，GM)是利用基因组信息进行优化的选种选配，可以有效控制群体近交水平的同时实现最大化的遗传进展。但基因组选配是对群体中所有个体进行选配，这与实际的育种工作有点相悖。本研究模拟了遗传力为0.5的9 000头个体的基础群数据，每个世代根据GEBV选择30头公畜、900头母畜作为种用个体，而后使用基因组选配、同质选配、异质选配、随机交配4种不同的选配方案。其中基因组选配中分别选取遗传进展最大的解、家系间方差最大的解、近交最小的解所对应的交配方案进行选育。每种方案选育5个世代，比较其后代群体的平均GEBV、每世代的遗传进展、近交系数、遗传方差，并重复5次取平均值。结果表明，3种基因组选配方案的ΔG均显著高于随机交配和异质选配(P < 0.01)，而且，选取遗传进展最大的基因组选配方案的ΔG比同质选配还高出4.3%。3种基因组选配的方案的ΔF比同质选配低22.2%~94.1%，而且选取近交最小的基因组选配方案ΔF比异质选配低11.8%。同质选配的遗传方差迅速降低，在第5世代显著低于除基因组选配中选择遗传进展最大的方案以外的所有方案(P < 0.05)，3种基因组选配方案的遗传方差比同质选配高10.8%~32.2%。这表明基因组选配不仅可以获得比同质选配更高的遗传进展，同时有效的降低了近交水平，并且减缓了遗传方差降低速度，保证了一定的遗传变异。基因组选配作为一种有效的可持续育种方法，在畜禽育种中开展十分有必要。
关键词：模拟数据    基因组选择    基因组选配    遗传进展    近交    
Simulation Study on the Effects of Different Mating Schemes Based on Genomic and Pedigree Information
ZHANG Pengfei1, HE Jun2, WANG Lixian1, ZHAO Fuping1     
1. Key Laboratory of Animal Genetics, Breeding and Reproduction(Poultry) of Ministry of Agriculture, Institute of Animal Science, Chinese Academy of Agricultural Sciences, Beijing 100193, China;
2. College of Animal Science and Technology, Hunan Agricultural University, Changsha 410128, China
Corresponding author: WANG Lixian, E-mail: wlxians@263.net; ZHAO Fuping, E-mail: haofuping@caas.cn.
Abstract: Genomic mating (GM) is the optimized selection and matching using genomic information, which can effectively control the level of population inbreeding and maximize genetic gain. Genomic mating is based on all individuals in the population, which is a little contrary to the actual breeding work. This study simulated the basic group data of 9 000 individuals with a heritability of 0.5. According to GEBV, 30 sire and 900 dam were selected for each generation as breeding individuals, and then 4 different mating schemes were used: genomic mating, positive assortative mating, negative assortative mating and random mating. Among them, 3 different schemes were given in genomic mating, namely, the maximum genetic gain, the minimum inbreeding, and the maximum variance between families. Five generations were breeding for each scheme, and the average GEBV, genetic gain, inbreeding coefficient, and genetic variance of the offspring population were compared, and the average was taken for 5 times. The ΔG of the 3 genomic mating schemes were significantly higher than those of random mating and positive assortative mating (P < 0.01). The ΔG of the genomic mating scheme with the maximum genetic gain was 4.3% higher than that of positive assortative mating. The ΔF of the 3 genomic mating schemes of were 22.2%-94.1% lower than those of positive assortative mating. Among them, the ΔF of the minimum inbreeding scheme selected in genomic mating was 11.8% lower than that of negative assortative mating. The genetic variance of positive assortative mating decreased rapidly and was significantly lower in the 5th generation than all schemes except the scheme that selected the maximum genetic gain in genomic mating (P < 0.05). The genetic variance of the 3 schemes of genomic mating was 10.8%-32.2% higher than that of positive assortative mating. The result indicate that genomic mating can not only obtain higher genetic gain than positive assortative mating, but also effectively reduce the rate of inbreeding, and slow down the rate of genetic variance reduction to ensure a certain genetic variation. As an effective sustainable breeding method, genomic mating is very necessary in livestock and poultry breeding.
Key words: simulation data    genomic selection    genomic mating    genetic gain    inbreeding    

基因组选择可以开展早期选择从而缩短世代间隔，降低孟德尔抽样(Mendelian sampling)误差，提高选择准确性来加快遗传进展[1-4]。然而，基因组选择是根据基因组育种值(genomic estimated breeding value，GEBV) 大小进行选留，但通常GEBV高的个体之间亲缘关系也比较高，经过多世代选育后就会降低群体遗传多样性、增加后代近交程度和纯合有害等位基因等问题，难以实现长期可持续的遗传进展[5]。于此，2016年Akdemir和Sánchez[6]提出了基因组选配(genomic mating，GM)，该方法利用基因组信息比较亲本可能的交配方案产生后代的育种值、近交和遗传方差，从而选择最佳的亲本交配组合方案。

在基因组选配提出之前，主要是利用系谱信息进行优化的选种选配，如最佳遗传贡献选择(optimal contribution selection，OCS)，是将选择反应和近交组合成候选亲本遗传贡献的函数，以平衡遗传进展、近交和共祖系数[7-10]。最佳遗传贡献选择在动物育种中应用较多，用以改良近交水平较高的群体。最佳遗传贡献选择理论提出后被不断改进，并且加入一些额外的约束条件进行优化[15-17]，其中包括有最小共祖选配(minimum coancestry，MC)和最小化祖先间遗传贡献的协方差(minimising the covariance between ancestral contributions，MCAC)。通过增加具有遗传贡献祖先的独立性和降低它们之间的混乱性来实现低近亲繁殖率，分散了它们在育种种群中的贡献，从而增加了每个后代具有贡献的祖先数量。这使得祖先更接近确切的阈值线性关系，从而降低近亲繁殖率[18-19]。Kinghorn等[20-22]使用配偶选择来最大化预测后代的价值。配偶选择包括两个组成部分：1)配偶选择指数(MSI)；2)用于寻找最大化MSI的配偶集合的配偶选择算法。这些策略被称为前瞻性配偶选择(look ahead mate selection，LAMS)[23]。

基因组选配充分地利用基因组信息来计算亲本间的遗传关系，并结合标记效应来决定哪些基因组合来获得下一个优秀的育种群体。基因组选配可以控制群体近交的增长速率，维持遗传多样性，同时实现长期且可持续的遗传进展[24-26]。然而基因组选配是对群体中所有个体进行选配，找到最优的交配组合，这与实际的育种工作有点相悖。因此，本研究将通过计算机模拟在选择GEBV排名靠前的最优秀的个体后，比较不同的选配方案下后代群体的遗传进展、近交系数、遗传方差的变化情况，评估基因组选配的效果，以期为在畜禽育种中开展基因组选配提供参考。

1 材料与方法 1.1 基础群个体数据的模拟

本研究使用QMSim模拟软件[27]进行基础群(第0世代)个体数据的模拟。模拟过程分两步进行，第一步模拟历史群体建立突变漂移平衡，第二步生产近代群体。本研究设性状的表型方差σP2=1 000，遗传力h2=0.5，遗传方差为σG2=h2σP2=500，环境方差为σe2=σp2-σG2=500，并且假设环境方差在各个世代保持不变。具体过程如下：1)历史群体的模拟：初始群体数量设置为2 000头，模拟1 000个世代。第1 000世代群体数量为2 000头，公母比为1∶1，再经过1 000个世代群体大小逐渐减小为400头，再进化1 000个世代，最后一代群体数量为2 050头，公畜为50头，总共2 050头个体用于近代群体的繁育。2)近代群体的模拟公畜为30头，母畜为900头，产仔数设为10头，后代公母比为1∶1。交配方式为随机交配。模拟2个世代，输出第2个世代9 000个个体的系谱和基因型数据，作为基础群个体，基因组参数见表 1。

表 1 基因组参数设置 Table 1 Genome parameter settings
1.2 GEBV估计及其个体选留

本研究使用BayesB方法计算基因组估计育种值(GEBV)。将基础群中具有表型值和基因型的9 000头个体作为参考群，使用R语言软件包BGLR[28]计算标记效应，Bayes模型参数设定迭代次数为20 000次，预烧(burn-in)为1 000次，并将公畜和母畜根据GEBV高低进行排序，选出GEBV排名前30头公猪、900头母猪作为种用个体繁育下一代。

在每个世代中，都采用上述方案选留个体。将每个世代中有表型和基因型的个体加入到参考群中，用于参考群的更新，并且每个世代重新估计标记效应。

1.3 基因组选配

本研究在基因组选配的目标函数中考虑遗传进展、近交系数和家系间方差来优化选配，遗传进展和近交系数的具体计算公式如下：

$ \begin{gathered} Inbreeding({\boldsymbol{P}})=1_{N_c}^{\prime}\left({\boldsymbol{P G}} {\boldsymbol{P}}^{\prime}+D\right) 1_{N_c} \\ {Gain}({\boldsymbol{P}})=1_{N_c}^{\prime} {\boldsymbol{P M}} \\ {Var}({\boldsymbol{P}})={\boldsymbol{P}} {\boldsymbol{G}} {\boldsymbol{P}}^{\prime}+D \end{gathered} $

其中，P为Nc×N的交配矩阵，N为亲本的个数，Nc为后代的数量；G为基因组关系矩阵；D为孟德尔抽样离差；M为基因型矩阵。

使用R包TrainSel[29]进行基因组选配。基因组关系矩阵(genomic relationships matrix，G)使用VanRaden[30]文章中的公式计算，通过R包rrBLUP[31]完成。参数设置：公畜30，母畜900，交配组合数设置为900，遗传算法参数中群体大小设置为200，迭代次数设置为800，其余参数设为默认值。

1.4 传统选配方式

1.4.1 随机交配 　　对选留的个体以随机交配的原则进行交配。

1.4.2 同质选配 　　根据个体的GEBV大小进行排序，将公畜按照降序的顺序与按照降序排序的母畜依次进行交配，每头公畜配30个母畜。

1.4.3 异质交配 　　根据个体的GEBV大小进行排序，将公畜按照升序的顺序与按照降序排序的母畜依次进行交配，每头公畜配30头母畜。

1.5 后代基因型、育种值和表型模拟

1.5.1 后代个体基因型的模拟 　　后代从亲本继承了基因座上的等位基因，遵循孟德尔遗传的原理。在使用QMSim模拟基础群数据(第0世代)时，会给出父母的单倍型，即每个位点用双等位基因(1和2)表示，第一个等位基因来自父亲，第二个等位基因来自母亲，因此，可以根据父母的基因型来推断模拟后代的基因型。具体过程[32]：1)对于第一个位点：产生均匀分布随机数U(0, 1)μ，如果μ < 0.5，则个体第一个位点上的第一个等位基因来自父亲的第一个染色体上的第一个位点，如果μ>0.5，则个体第一个位点上的第一个等位基因来自父亲的另一个染色体上的第一个位点。2)对于第i(i=2, …, N)个位点，首先计算第i个位点与第i-1个位点之间的重组率，根据Haldane[33]研究中提出的作图函数计算两个座位间的重组率r：$r=\frac{1}{2}\left(1-e^{-2 \mathrm{c}}\right)$，其中，c为第i个位点与第i-1个位点之间的遗传距离(以摩尔根为单位)。然后重新生成均匀分布随机数U(0, 1)μ，如果μ>r，则不发生重组，个体第i个位点第一个等位基因来自父亲的第一个染色体上的第i个位点，如果μ < r，则发生重组，个体第i个位点第一个等位基因来自父亲的另一个染色体上的第i个位点。3)剩余标记依次类推。4)个体的第二个等位基因来自母亲，与上述过程相同。

1.5.2 后代个体育种值和表型值的模拟 　　个体i真实育种值用以下模型模拟[34]：

$ g_i=\frac{1}{2} \mu_s+\frac{1}{2} \mu_d+w_i $

其中，μs和μd分别是父亲和母亲的育种值，wi是个体i的孟德尔抽样离差，wi~N(0, σw2)，其中σw2= $\frac{1}{4}\left(1-f_s\right) \sigma_a^2+\frac{1}{4}\left(1-f_d\right) \sigma_a^2$，fs和fd分别为个体i父亲和母亲的近交系数，σa2为基础群中性状的遗传方差。近交系数计算公式[35]：

$ F_{\rm {PED }}=\sum\left(\frac{1}{2}\right)^N\left(1+F_A\right) $

其中，FPED是个体的近交系数，N是个体的父亲到共同祖先的相关通径链的数量，FA是共同祖先A的近交系数。

个体i性状表型值用以下模型模拟：

$ y_i=\mu+g_i+e_i $

其中，yi是个体i的表型值；μ是群体均值；gi是个体i的随机加性遗传效应(育种值)；ei为个体i的随机残差，对于各个世代，ei服从N(0，σe2)分布。

以上过程通过R语言自写程序实现。

1.6 评估标准

1.6.1 遗传进展的计算 　　每个世代的遗传进展计算公式如下：

$ \Delta G=\bar{a}_u-\bar{a}_{u-1} $

其中，a为该世代的平均基因组估计育种值(GEBV)，u为世代数。

1.6.2 近交系数的计算 　　本研究计算了2种近交系数，第一种是由Wright[35]提出的系谱近交系数(FPED)，其计算公式：

$ F_{\mathrm{PED}}=\sum\left(\frac{1}{2}\right)^N\left(1+F_A\right) $

其中，FPED是个体的近交系数，N是个体的父亲到共同祖先的相关通径链的数量，FA是共同祖先A的近交系数。

第二种，基于SNPs估计的近交系数(FGRM)，其计算公式[36]：

$ F_{\mathrm{GRM}}=\sum\limits_{i=1}^m\left(\left[x_i-E\left(x_i\right)\right]^2 /\left[2 p_i\left(1-p_i\right)-1\right]\right) / m $

其中，m是SNP的数量，pi是等位基因频率，xi是第i个SNP的拷贝数。

近交系数每世代增长量(ΔF)计算公式[37]：

$ \Delta F=1-e^\beta $

其中β是ln(1-Fu)在u世代的线性回归的斜率，Fu是在u世代出生的动物的平均近交系数。

1.6.3 后代遗传方差的计算 　　本研究将每个世代9 000头个体的基因组估计育种值(GEBV)的方差作为群体的遗传方差。计算公式：

$ \sigma_g^2=\sum\limits_{i=1}^n\left(a_i-\bar{a}\right)^2 /(n-1) $

其中，n为该世代所有个体的总数，a为个体i的基因组估计育种值(GEBV), a为该世代所有个体的基因组估计育种值(GEBV)的平均值。

1.7 模拟试验

本研究假设世代间不重叠，每个世代群体规模设置为9 000。每个世代选出GEBV排名前30个公畜和前900个母畜作为种用个体繁育下一代，后代数设置为10，具体过程见图 1。每种方案模拟选育5个世代，并计算每代群体的平均GEBV、遗传进展、近交系数以及遗传方差，重复5次取平均值，并且在每个世代对不同选配方案的平均GEBV、近交系数以及遗传方差进行T检验。

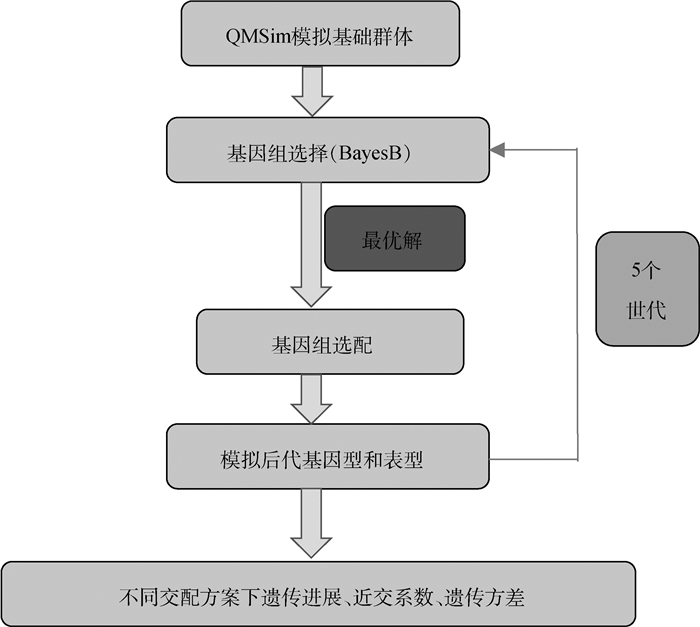
图 1 模拟试验技术路线 Fig. 1 Technical schematic of simulation study

本研究在Linux系统下通过调用R统计编程语言编写完成的所有数据模拟和计算的脚本实现，Linux服务器配置为40核2.40 GHz Intel(R) Xeon(R) Gold 6148的处理器和768 GB内存。

2 结果 2.1 基因组选配方案的确定标准

本研究采用遗传进展、近交和家系间方差3个因素对选择效果进行评估，三者之间并不是独立的，而是彼此间相互牵制。TrainSel通过对这3个指标进行优化权衡后会得出一系列帕累托最优解(pareto optimality)，通过三维图可以表示(图 2)。图中的每一个点都对应着该3个指标下的一组交配组合，在没有其他限定条件下，图上的曲面上所有的点都可以作为一个交配方案。本研究根据这3个指标指定的不同交配方案，在每个世代分别选取遗传进展最大的交配方案、家系间方差最大的交配方案、近交最小的交配方案进行连续5个世代的选育。

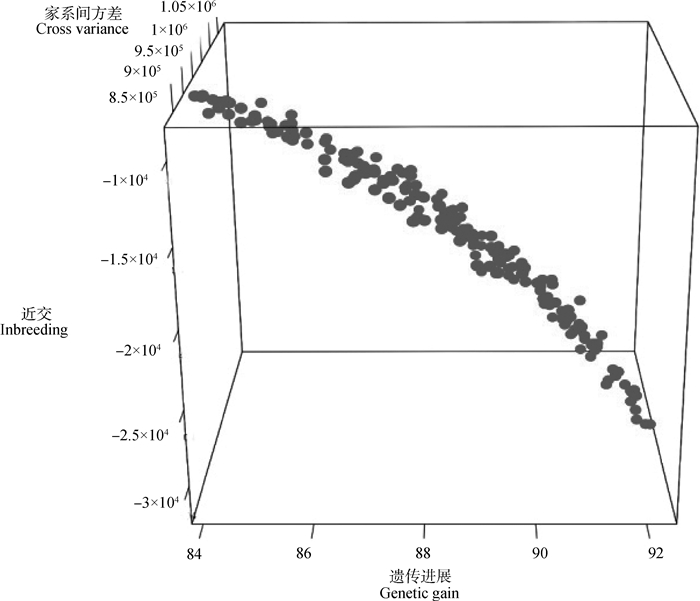
图 2 基因组选配计算得到的最优解 Fig. 2 The optimal solution of genomic mating
2.2 遗传趋势和平均每世代的遗传进展

图 3比较了6种方案在5个世代中的遗传趋势。基因组选配中选取遗传进展最大的方案在每个世代的平均GEBV均极显著高于随机交配和异质选配(P < 0.01)，在第1世代均极显著高于其它选配方案(P < 0.01)，在1~4世代的平均GEBV均显著高于基因组选配中选取近交最小的方案(P < 0.05)，在第1、2世代显著高于基因组选配中选取方差最大的方案(P < 0.05)。基因组选配中选取近交最小的方案在第2世代高于异质选配(P < 0.01)。基因组选配中选取方差最大的方案在第4、5世代的平均GEBV高于异质选配(P < 0.05)。

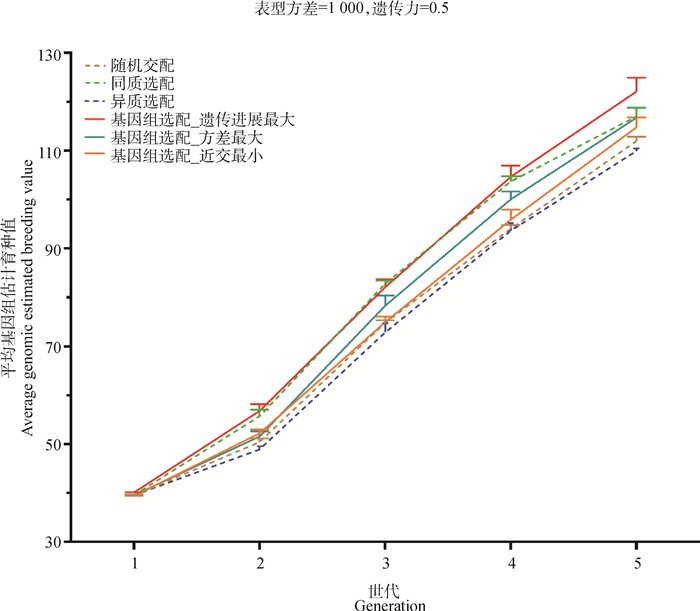
图 3 遗传力为0.5时6种不同交配方案经过5个世代选育后的遗传趋势 Fig. 3 Genetic trend of 6 mating schemes over 5 generations at heritability of 0.15

不同选配方案的ΔG如表 2所示，经过5个世代的选育，基因组选配的3种方案的ΔG均显著高于随机交配和异质选配(P < 0.01)，其中，基因组选配中选取遗传进展最大的方案的ΔG高于同质选配，比同质选配高4.3%。

表 2 遗传力为0.5时6种不同选配方案重复5次后平均每个世代的遗传进展和标准差 Table 2 Average rate of genetic gain (ΔG) and standard deviation for each generation after 5 repeats of 6 different mating schemes at heritability of 0.5
2.3 近交系数的变化趋势和平均每世代的近交增长量

不同选配方案的5个世代的平均系谱近交系数(FPED)如图 4所示，同质选配在每个世代的平均FPED均极显著高于随机和异质选配和基因组选配中选择近交最小的方案(P < 0.01)，显著高于基因组选配中选择遗传进展最大的方案和基因组选配中选择家系间方差最大的方案(P < 0.05)。

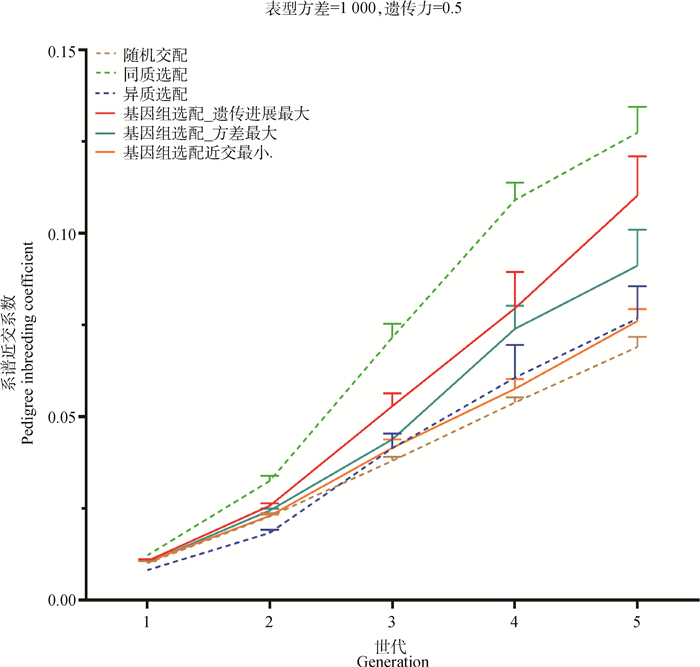
图 4 遗传力为0.5时6种不同交配方案经过5个世代选育后的平均系谱近交系数变化趋势 Fig. 4 Trends of average pedigree inbreeding coefficient of 6 mating schemes over 5 generations at heritability of 0.5

不同选配方案的ΔF如表 3所示，经过5个世代的选育，基因组选配的3种方案的ΔF比同质选配低22.2%~94.1%。其中基因组选配_近交最小方案的ΔF比异质选配低11.8%。

表 3 遗传力为0.5时6种不同选配方案重复5次后平均每个世代的近交增量和标准差 Table 3 Average rate of inbreeding (ΔF) and standard deviation for each generation after 5 repeats of 6 different mating schemes at heritability of 0.5
2.4 遗传方差的变化趋势

不同选配方案的平均遗传方差变化趋势如图 5所示，同质选配在第1世代极显著高于其它选配方案(P < 0.01)，随着选育的进行，同质选配的遗传方差迅速降低，在第5世代显著低于除基因组选配中选择遗传进展最大的方案以外的所有方案(P < 0.05)。经过5个世代的选育，基因组选配的3种方案的遗传方差比同质选配高10.8%~32.2%。

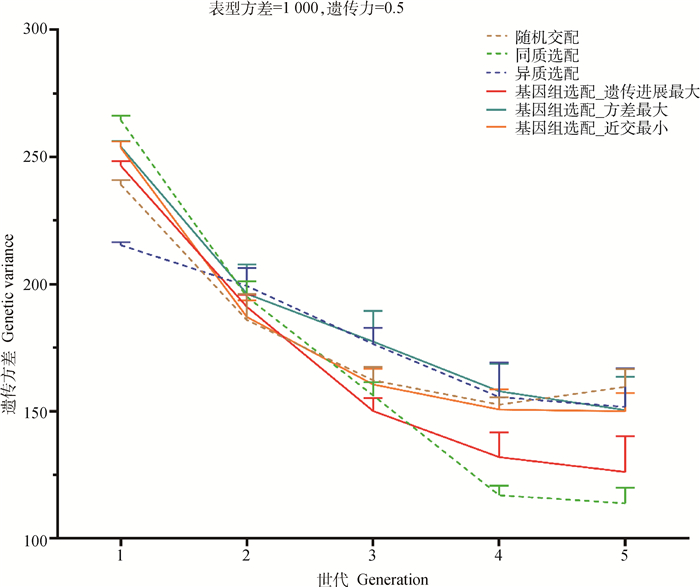
图 5 遗传力为0.5时6种不同交配方案经过5个世代选育后的平均遗传方差的变化趋势 Fig. 5 Trends of average genetic variance of 6 mating schemes over 5 generations at heritability of 0.5
3 讨论

本研究使用模拟数据比较了使用基因组选择留种后，使用基因组选配进行最优的配对组合的效果，并与传统选配方案进行了比较。在评估不同选配方案后代群体近交水平时，计算了系谱近交系数(FPED)和基因组近交系数(FGRM)，但是基因组近交系数(FGRM)计算结果是负值，这与其它研究报道一致[38-40]。因此本研究中主要以系谱近交系数进行讨论。综合来看，基因组选配能取得比其它3种方案更高的遗传进展，近交水平远低于同质选配，接近异质选配，而遗传方差下降幅度小于同质选配，高于异质选配和随机交配。这表明基因组选配不仅能获得足够大的遗传进展，有效的控制群体近交，还能保持群体内的遗传变异。

TrainSel在计算最优的交配组合时，公畜和母畜的数量、配对数、SNP的数量以及遗传算法参数中群体大小和迭代次数都对计算速度有影响。而且遗传算法参数中群体大小和迭代次数直接决定了是否能获得理想的结果。本研究中，每个世代选留30头公畜和900头母畜，以及配对数设置为900，就存在27 000个可能的配对组合，这需要大量的计算时间去对每个组合所得结果进行预测。经过前期试验发现，TrainSel中遗传算法参数中群体大小设置为200和迭代次数设置为500以上才能获得较为理想的结果。本研究对群体大小设置和迭代次数分别设置为200和800，这都会大大增加计算时间。因此，在本研究中只模拟了一条染色体上的500个标记位点作为参考，每次计算最优交配组合需要时间约24 h左右。为了验证结果的广谱性，又对群体大小为1 500头，选择GEBV排名靠前的10头公畜、150头母畜作为种用个体，SNP位点数为1 500个时，基因组选配效果的模拟研究。由于时间的限制，只将第一个世代的结果进行了总结(图 6)，结果发现，此种情况下不同选配方案的变化趋势与SNP位点数为500和群体为9 000时的基本一致。

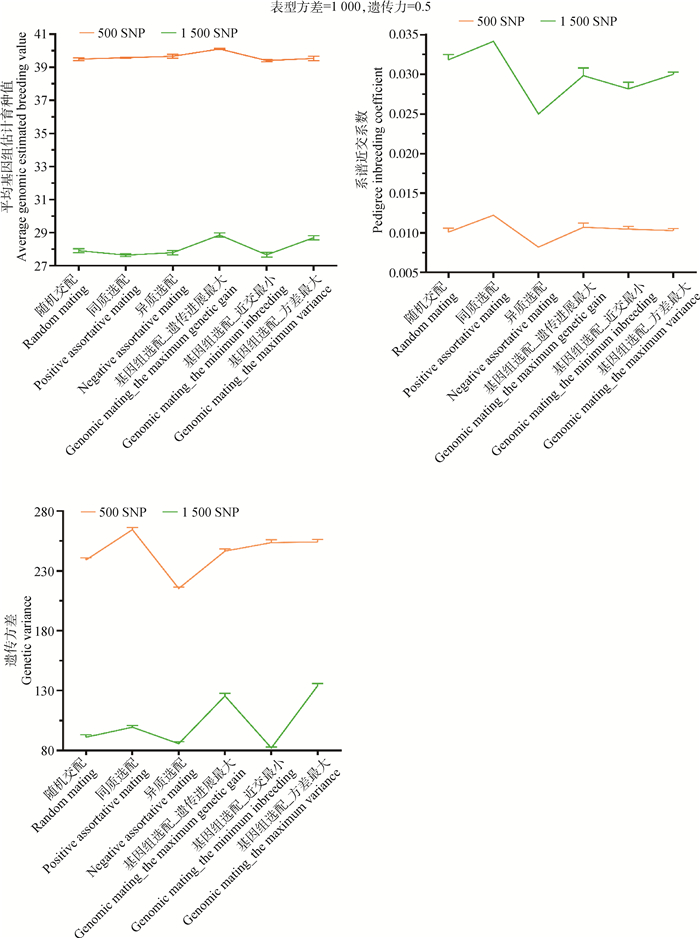
图 6 SNP为500和1 500时6种不同选配方案在第1个世代的平均GEBV、系谱近交系数和遗传方差 Fig. 6 Average GEBV, pedigree inbreeding coefficient and genetic variance in the first generation for 6 different mating schemes at SNP of 500 and 1 500, respectively

本研究通过基因组育种值进行选留个体，然后采用R包TrainSel提供的基因组选配方法得到最优的交配组合，这些交配组合并不唯一，但是都比其他的选配方案的效果要好。该方法与其他算法如最佳遗传贡献选择[11-13]还在存在明显的不同，最佳遗传贡献选择只是给出了候选亲本对后代的遗传贡献比例，没有给出具体的配对组合。但是基因组选配通过构建交配矩阵，把焦点问题转移到配偶的选择上。通过基因组选配可以计算出父母贡献比例，但是无法从遗传贡献比例计算出最优的交配组合。

目前基因组选配还处于计算机模拟阶段，在真实数据上的研究不多。基因组选配比基因组选择需要考虑更多问题，既需要考虑个体本身的遗传，也需要考虑配对间的互补关系，以及一些品种的特性，从而使群体近交水平降低以及基因频率的改变。因此，基因组选配是一个非常复杂的问题。目前本研究只是针对单性状的加性遗传效应，除了用于优化选配方案外，基因组选配还可以用来估计杂交动物、预测高产或低产个体出现的概率等或其他应用领域[24]。目前基因组选配还处于初步研究阶段，仍然存在许多问题需要深入地探索。

4 结论

本研究通过对基因组选择下不同的基因组选配方案经过5个世代的遗传进展、近交系数、遗传方差进行比较得出，相对于其它交配方案，在实际的育种中基因组选配方案具有明显的优势。基因组选配中选取遗传进展最大方案的ΔG比同质选配高4.3%，ΔF比同质选配低22.2%，遗传方差比同质选配高10.8%。基因组选配作为一种有效的可持续育种方法，在动物育种中开展十分有必要。基因组选配同时考虑了亲缘和价值育种，不仅可以获得较高的遗传进展，同时可以有效的控制群体的近交水平，并且考虑了家系间方差，保证了一定的遗传变异，是一种可行的可持续育种方法。以上研究为下一步在畜禽育种中开展基因组选配提供了参考。

参考文献
[1]
MEUWISSEN T H E, HAYES B J, GODDARD M E. Prediction of total genetic value using genome-wide dense marker maps[J]. Genetics, 2001, 157(4): 1819-1829. DOI:10.1093/genetics/157.4.1819
[2]
MEUWISSEN T, HAYES B, GODDARD M. Accelerating improvement of livestock with genomic selection[J]. Annu Rev Anim Biosci, 2013, 1: 221-237. DOI:10.1146/annurev-animal-031412-103705
[3]
TESSEMA B B, LIU H M, SØRENSEN A C, et al. Strategies using genomic selection to increase genetic gain in breeding programs for wheat[J]. Front Genet, 2020, 11: 578123. DOI:10.3389/fgene.2020.578123
[4]
SAMORÈ A B, BUTTAZZONI L, GALLO M, et al. Genomic selection in a pig population including information from slaughtered full sibs of boars within a sib-testing program[J]. Animal, 2015, 9(5): 750-759. DOI:10.1017/S1751731114002924
[5]
JANNINK J L. Dynamics of long-term genomic selection[J]. Genet Sel Evol, 2010, 42(1): 35. DOI:10.1186/1297-9686-42-35
[6]
AKDEMIR D, SÁNCHEZ J I. Efficient breeding by genomic mating[J]. Front Genet, 2016, 7: 210.
[7]
WRAY N R, GODDARD M E. Increasing long-term response to selection[J]. Genet Sel Evol, 1994, 26(5): 431-451. DOI:10.1186/1297-9686-26-5-431
[8]
MEUWISSEN T H E, SONESSON A K. Maximizing the response of selection with a predefined rate of inbreeding: overlapping generations[J]. J Anim Sci, 1998, 76(10): 2575-2583. DOI:10.2527/1998.76102575x
[9]
MEUWISSEN T H E. Maximizing the response of selection with a predefined rate of inbreeding[J]. J Anim Sci, 1997, 75(4): 934-940. DOI:10.2527/1997.754934x
[10]
SÁNCHEZ-MOLANO E, PONG-WONG R, BANOS G. Genomic-based optimum contribution in conservation and genetic improvement programs with antagonistic fitness and productivity traits[J]. Front Genet, 2016, 7: 25.
[11]
HOWARD D M, PONG-WONG R, KNAP P W, et al. Selective advantage of implementing optimal contributions selection and timescales for the convergence of long-term genetic contributions[J]. Genet Sel Evol, 2018, 50(1): 24. DOI:10.1186/s12711-018-0392-z
[12]
CLARK S A, KINGHORN B P, HICKEY J M, et al. The effect of genomic information on optimal contribution selection in livestock breeding programs[J]. Genet Sel Evol, 2013, 45(1): 44. DOI:10.1186/1297-9686-45-44
[13]
HAMILTON M G. Optimal contribution selection in highly fecund species with overlapping generations[J]. J Hered, 2020, 111(7): 646-651. DOI:10.1093/jhered/esaa051
[14]
OLSEN H F, MEUWISSEN T, KLEMETSDAL G. Optimal contribution selection applied to the Norwegian and the North-Swedish cold-blooded trotter - a feasibility study[J]. J Anim Breed Genet, 2013, 130(3): 170-177. DOI:10.1111/j.1439-0388.2012.01005.x
[15]
PONG-WONG R, WOOLLIAMS J A. Optimisation of contribution of candidate parents to maximise genetic gain and restricting inbreeding using semidefinite programming (Open Access publication)[J]. Genet Sel Evol, 2007, 39(1): 3. DOI:10.1186/1297-9686-39-1-3
[16]
AHLINDER J, MULLIN T J, YAMASHITA M. Using semidefinite programming to optimize unequal deployment of genotypes to a clonal seed orchard[J]. Tree Genet Genomes, 2014, 10(1): 27-34. DOI:10.1007/s11295-013-0659-z
[17]
WOOLLIAMS J A, BERG P, DAGNACHEW B S, et al. Genetic contributions and their optimization[J]. J Anim Breed Genet, 2015, 132(2): 89-99. DOI:10.1111/jbg.12148
[18]
SØRENSEN A C, BERG P, WOOLLIAMS J A. The advantage of factorial mating under selection is uncovered by deterministically predicted rates of inbreeding[J]. Genet Sel Evol, 2005, 37(1): 57. DOI:10.1186/1297-9686-37-1-57
[19]
LIU H, HENRYON M, SØRENSEN A C. Mating strategies with genomic information reduce rates of inbreeding in animal breeding schemes without compromising genetic gain[J]. Animal, 2017, 11(4): 547-555. DOI:10.1017/S1751731116001786
[20]
KINGHORN B P, SHEPHERD R K. Mate selection for the tactical implementation of breeding programs[J]. Assoc Adv Anim Breed Genet, 1999, 13: 130-133.
[21]
KINGHORN B P. Mate selection by groups[J]. J Dairy Sci, 1998, 81(2): 55-63.
[22]
KINGHORN B P. An algorithm for efficient constrained mate selection[J]. Genet Sel Evol, 2011, 43(1): 4. DOI:10.1186/1297-9686-43-4
[23]
MOEINIZADE S, HU G P, WANG L Z, et al. Optimizing selection and mating in genomic selection with a look-ahead approach: An operations research framework[J]. G3 (Bethesda), 2019, 9(7): 2123-2133. DOI:10.1534/g3.118.200842
[24]
何俊, LOPES F B, 吴晓林. 动物基因组选配方法与应用[J]. 遗传, 2019, 41(6): 486-493.
HE J, LOPES F B, WU X L. Methods and applications of animal genomic mating[J]. Hereditas (Beijing), 2019, 41(6): 486-493. DOI:10.16288/j.yczz.19-053 (in Chinese)
[25]
高振东, 何俊. 基因组选配: 基因组时代的高效育种[J]. 黑龙江畜牧兽医, 2019(24): 61-64, 175.
GAO Z D, HE J. Genome matching: Efficient breeding in the genome era[J]. Heilongjiang Animal Science and Veterinary Medicine, 2019(24): 61-64, 175. (in Chinese)
[26]
AKDEMIR D, BEAVIS W, FRITSCHE-NETO R, et al. Multi-objective optimized genomic breeding strategies for sustainable food improvement[J]. Heredity (Edinb), 2019, 122(5): 672-683. DOI:10.1038/s41437-018-0147-1
[27]
SARGOLZAEI M, SCHENKEL F S. QMSim: A large-scale genome simulator for livestock[J]. Bioinformatics, 2009, 25(5): 680-681.
[28]
PÉREZ P, DE LOS CAMPOS G. Genome-wide regression and prediction with the BGLR statistical package[J]. Genetics, 2014, 198(2): 483-495.
[29]
AKDEMIR D, RIO S, SÁNCHEZ J I Y. TrainSel: an R package for selection of training populations[J]. Front Genet, 2021, 12: 655287.
[30]
VANRADEN P M. Efficient methods to compute genomic predictions[J]. J Dairy Sci, 2008, 91(11): 4414-4423.
[31]
ENDELMAN J B. Ridge regression and other kernels for genomic selection with R package rrBLUP[J]. Plant Genome, 2011, 4(3): 250-255.
[32]
张勤. 动物遗传育种中的计算方法[M]. 北京: 科学出版社, 2007.
ZHANG Q. The calculation method in animal genetic breeding[M]. Beijing: Science Press, 2007. (in Chinese)
[33]
HALDANE J B S. The combination of linkage values, and the calculation of distances between the loci of linked factors[J]. J Genet, 1919, 8: 299-309.
[34]
ZHAO F P, ZHANG Q. Stimulation study of gene pyramiding in animals by marker-assisted selection[J]. J Integr Agric, 2012, 11(11): 1871-1876.
[35]
WRIGHT S. Coefficients of inbreeding and relationship[J]. Am Nat, 1922, 56(645): 330-338.
[36]
YANG J, LEE S H, GODDARD M E, et al. GCTA: a tool for genome-wide complex trait analysis[J]. Am J Hum Genet, 2011, 88(1): 76-82.
[37]
NIREA K G, SONESSON A K, WOOLLIAMS J A, et al. Effect of non-random mating on genomic and BLUP selection schemes[J]. Genet Sel Evol, 2012, 44(1): 11.
[38]
SOLÉ M, GORI A S, FAUX P, et al. Age-based partitioning of individual genomic inbreeding levels in Belgian Blue cattle[J]. Genet Sel Evol, 2017, 49(1): 92.
[39]
VILLANUEVA B, FERNÁNDEZ A, SAURA M, et al. The value of genomic relationship matrices to estimate levels of inbreeding[J]. Genet Sel Evol, 2021, 53(1): 42.
[40]
ZHANG Q Q, CALUS M P L, GULDBRANDTSEN B, et al. Estimation of inbreeding using pedigree, 50k SNP chip genotypes and full sequence data in three cattle breeds[J]. BMC Genet, 2015, 16: 88.

(编辑   郭云雁)