近年来,随着SNP芯片和全基因组测序技术的飞速发展,全基因组关联分析(genome-wide association study,GWAS)和基因组选择(genomic selection,GS)技术在遗传学领域和畜禽育种中得到了越来越广泛的应用[1-2]。如今,GWAS和GS主要是基于SNP芯片数据开展的,现有商业化SNP芯片一般都是基于一个或少数几个品种的信息构建而成,无法涵盖品种内基因组上的全部SNPs标记,具有确认偏倚性[3]。相比于SNP芯片数据,全基因组测序数据可以检测出所有碱基序列,包含所有导致遗传变异的多态性信息,还能结合稀有突变分析,从而提高基因组预测的准确性,尤其在基因组选择中具有巨大的优势[4-6]。目前,基于高覆盖测序数据对大群体开展GS和GWAS的成本依旧很高,一般是对低密度芯片或低覆盖测序数据进行填充来获得高密度芯片或高覆盖测序数据。基因型填充(genotype imputation,GI)技术,即利用现有的基因型信息,对未测定或者不完整的基因型进行计算推断,其基本原理是根据参考群体或群体内其他个体与目标群体的基因型数据内的连锁不平衡信息和重组率等构建共有的单倍型片段,然后利用单倍型片段信息对目标群体内未分型位点进行估算并填充完整[7-9]。
基因型填充技术现已广泛应用于各种基因型数据的处理,成为了一种重要且常规的工具[7]。基因型填充最初用于服务人类遗传学研究,例如,在人类疾病研究方面,利用填充后的数据进行精细定位,定位到了增加Ⅱ型糖尿病风险的关键基因[10],另外一项研究也定位到了控制血甘油三酯水平的主效基因GCKR的精确位置[11]。此外,研究人员也发现,基因型填充在动植物遗传育种方面具有重要的意义。在水稻相关的研究中,利用填充后的数据鉴定了多个对杂种优势产生影响的显性效应位点,并证明了这些优势等位基因的积累是导致杂种优势的重要因素[12]。有关奶牛泌乳性状的研究中,利用填充后的数据筛选出许多新的候选基因[13],将低密度芯片填充至高密度芯片后进行基因组选择即可以得到高准确性的估计育种值[14]。同样,在猪[15-16]、羊[17]、鸡[18]、鸭[19]的遗传育种研究中也都有着重要的应用。
影响基因型填充效果的因素有很多,包括参考群体大小[20]、标记最小等位基因频率[21](minor allele frequency, MAF)、目标群体与参考群体间的遗传关系[22]和填充算法[23]等。尽管已有研究对这些因素分别进行过探讨,却没有对这些因素进行综合研究比较,导致研究人员在填充时对影响因素的标准控制没有依据,无法确定填充结果是否可靠,使后续研究产生偏差。
本研究将利用模拟数据探究参考群体规模、目标群体与参考群体间遗传关系(距离)远近、目标群体位点数目(比例)、最小等位基因频率以及填充算法这几种因素对填充效果的影响,然后进行综合比较,以期获得一个优良可靠的填充策略所需最低标准。当所用实际数据符合该标准时,可以获得质量最佳的填充数据,确保后续研究顺利进行。
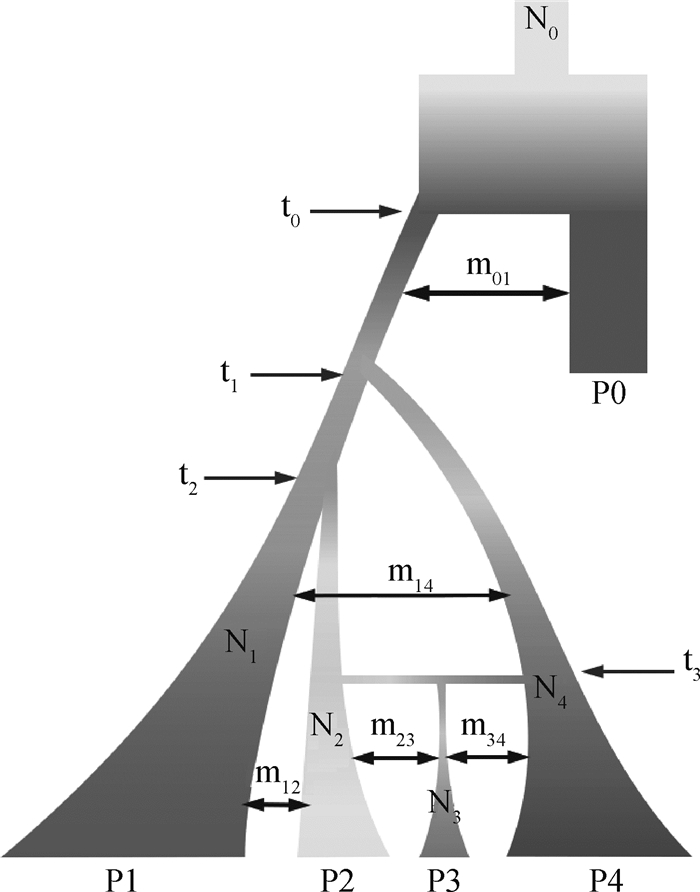
1 材料与方法 1.1 数据模拟本研究使用基于溯祖理论的Python软件包msprime[24]模拟群体遗传变化历史。为了使研究结果可以在动物群体中应用,模拟数据按照有代表性的猪群体遗传发育历史作为参考[25-27],由原始群体经过群体分化和突变迁移等历史最终形成4个群体,按群体间的亲缘关系远近顺序对群体命名为P1、P2、P3、P4,具体的群体结构见图 1。模拟出4个群体共20 000个,长度为10 Mb的二倍体样本序列数据,其中,P1群体中个体数目为11 000,P2、P3、P4群体个体数目分别为3 000,并以P1群体中的前1 000个个体作为填充目标群体,剩余的作为参考群体按照设定因素划分。
|
P.群体;N.有效群体大小;t.群体分化时间节点;m.群体间迁移率;颜色变化表示群体间遗传差异,分支的宽度与群体大小相对应,且时间经历由上至下,双箭头线段的粗细与迁移强度成正比 P. Populations; N. Effective population size; t. The time of population differentiation; m. Migration rate between populations; Color change indicates genetic difference between populations, branch width corresponding to population size, and time flowing from top to bottom. The width of the double arrows is proportional to the migration intensity 图 1 模拟群体结构模型示意图 Fig. 1 Schematic diagram of simulated population structure model |
在模拟出数据后,按填充策略所测量的因素对数据进行处理。首先,通过芯片数据构建亲缘关系矩阵,计算出群体间平均亲缘系数(表 1),来评估4个群体间的遗传距离是否与预设参数相符。如表 1所示,P2、P3、P4与P1群体的亲缘关系依次降低,说明遗传距离依次增加,与预设相符。根据目标群体与参考群体遗传距离由近及远设置P1、P2、P3、P4作为参考群体,分别剔除包含参考群体的每个群体中MAF < 0.01的位点;参考群体大小因素设置为100、1 000、3 000、5 000、10 000五个水平,其中P2、P3、P4群体只设置前3个水平;目标群体位点数目占参考群体位点数目的百分比设置为1%、5%、10%、30%、50%、90% 6个水平,数据的统计信息如表 2所示。
|
|
表 1 群体间亲缘关系 Table 1 The genetic relationship between pairs of populations |
|
|
表 2 模拟数据统计信息 Table 2 The summary statistics of simulation data |
随着基因型填充技术的应用,在近些年内各种各样的基因型填充方法也飞速发展,在填充速度、消耗内存和处理性能上都得到了显著的提升[28],然而应用最广泛也最准确的方法都是基于隐马尔可夫模型(hidden Markov Models, HMM)提出的。一般情况下,目标样本会被预先使用准确的方法[29-30]进行分型得到单倍型集群,称这个阶段为预分型,然后利用HMM对目标样本和参考面板的单倍型间的共享序列进行建模,HMM将每一个目标单倍型看作参考面板中单倍型的不完美镶嵌体,继而对基因组上每个位置输出参考面板中各个单倍型复制概率的向量,利用参考面板中的标记对该标记处未分型的等位基因进行加权预测并填充完整[9, 31-32]。本研究选择Beagle5.1(20Nov19.573)[33]和Minimac4 v1.0.0[34]作为填充软件,其中Beagle5.1需要的遗传图谱文件由虚拟数据的真实值制作,参考群体文件转换为Beagle特有的.bref3文件,Minimac4需要特定的参考文件格式.m3vcf由Minimac3制作,在填充时均使用5线程,其他参数为默认。所有程序在24核2.1Ghz Intel(R) Xeon(R) Silver 4116的128Gb戴尔工作站上运行。
1.4 填充效果评估为了比较两种填充算法的效果,以填充准确性、填充错误率和填充耗时3项统计结果作为评价标准。其中,填充准确性是指被填充的位点与真实位点之间相关性的平方(r2)。填充错误率是指填充错误的等位基因数目占总共被填充等位基因数目的百分比[35]。填充耗时为每次填充1 000个个体所消耗的时间。
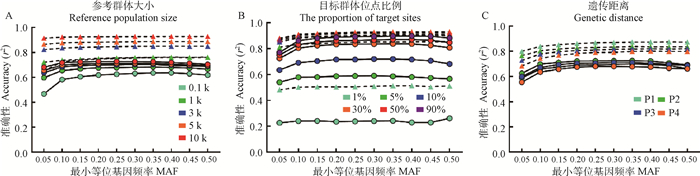
2 结果 2.1 各因素对基因型填充准确性的影响在其他因素相同时,参考群体大小在Beagle5.1和Minimac4中对填充的准确性均有极显著影响(P < 1×10-4),且呈现正相关关系(相关系数分别为r=0.954和r=0.769,后顺序相同)。由图 2A可以看出,随着参考群体内个体数量的增加,准确性有着显著的提高,参考群体由100(浅绿色标记线)增加到10 000(红色标记线),Beagle5.1和Minimac4的填充准确性分别由0.66和0.61增加到0.93和0.72。同样地,目标群体位点比例对准确性也有着极显著的影响(P < 1×10-4,r=0.722和r=0.905),目标群体位点比例与准确性呈正相关,当目标群体位点比例由1%(浅绿色标记线)升至90%(紫色标记线)时,Beagle5.1和Minimac的填充准确性分别由0.51和0.24增加到0.87和0.88(图 2B)。如图 2C所示,遗传距离只对Beagle5.1的填充准确性有显著影响(P < 1×10-4,r=-0.741),而对Minimac4的填充效果无显著影响(P=0.18),当参考群体由群体1变为群体4(遗传距离由近到远),Beagle5.1的填充准确性由0.84降低到0.77,而Minimac4的填充准确性仅从0.70略微降低至0.68。
|
A.参考群体大小对填充准确性的影响;B.目标群体位点比例对填充准确性的影响;C.参考群体和目标群体间的遗传距离对填充准确性的影响。三角形标志虚线代表Beagle5.1,圆形标志实线代表Minimac4。不同颜色的标志代表不同水平 A. The influence of reference population size on imputation accuracy; B. The influence of target population sites proportion on imputation accuracy; C. The influence of genetic distance between reference population and target population on imputation accuracy. The dotted lines with a triangle sign represent Beagle5.1, and the solid lines with a round sign represent Minimac4. Different colored signs represent different levels 图 2 不同因素对填充准确性的影响 Fig. 2 The influence of different factors on imputation accuracy |
在两个软件填充结果中发现,随参考群体大小、目标群体位点比例和遗传距离发生变化时,MAF的大小对填充准确性无显著影响(P>0.05),尽管MAF的大小与填充准确性无线性相关,但由图 2可以看出,随着MAF的增加,准确性呈现先上升后下降并总体上呈现增长的趋势。以图 2B中Minimac4填充下目标群体位点比例10%(蓝色标志实线)时为例,由MAF为0~0.05区间增至0.45~0.50区间,准确性由0.63增加至0.68,并于区间0.25~0.30时达到最高0.72,后略微下降。
根据以上结果,计算了各因素不同水平下影响准确性变化的变异系数。在Beagle5.1中,参考群体大小、目标群体位点比例和遗传距离对准确性影响的变异系数分别为0.116、0.172和0.046,在Minimac4中,参考群体大小和目标群体位点比例的变异系数分别为0.058和0.326。这些结果表明,尽管参考群体大小和目标群体位点比例对填充准确性都有很大的影响,但其中目标群体位点比例是影响填充准确性的最主要因素。如表 3所示,仅当参考群体较小,且目标群体标记比例较高时,Minimac4的填充准确性才高于Beagle5.1,且Beagle5.1和Minimac4填充的准确性范围分别为0.14 < r2 < 0.97和0.14 < r2 < 0.89。如果要求填充后的数据达到理想状态,需要填充的准确性大于0.85,则在表 3中观察到,利用Beagle5.1填充时,参考群体大小需要达到1 000,同时目标群体标记比例约为30%,或当参考群体大小增加时目标群体标记比例的标注可适当降低;利用Minimac4填充时,目标群体标记比例需要达到90%,或者可适当增加参考群体以调整目标群体标记比例降低对准确性的影响。
|
|
表 3 不同水平填充准确性统计信息 Table 3 The statistics of imputation accuracy at different levels |
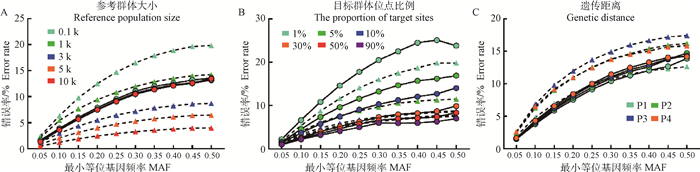
其他因素都相同的情况下,参考群体大小对Beagle5.1填充的错误率有极显著的影响(P < 1×10-4),且呈现负相关(r=-0.759);而对Minimac4填充的错误率没有显著影响(P=0.81)。由图 3A可以看出,随着参考群体内个体数量的增加,错误率显著下降,参考群体由100(浅绿色标记线)增加到10 000(红色标记线),Beagle5.1的填充错误率由13.9%降低到2.8%,而Minimac4中却几乎完全没有变化。如图 3B显示,目标群体位点比例对Beagle5.1和Minimac4的填充错误率均有着极显著的影响(P < 1×10-4,r=-0.516和r=-0.651),目标群体位点比例与错误率在总体上呈负相关,就是说填充错误率随着目标群体位点比例增加而降低,当目标群体位点比例由1%(浅绿色标记线)升至90%(紫色标记线)时,Beagle5.1和Minimac4的填充错误率分别由13.4%和16.9%降低到6.0%和4.7%。遗传距离对Beagle5.1和Minimac4的填充错误率都没有显著影响(P=0.17和P=0.65),但在Beagle5.1中,仅当参考群体为群体1时有较低的平均错误率为8.8%(图 3C)。
|
A.参考群体大小对填充错误率的影响;B.目标群体位点比例对填充错误率的影响;C.参考群体和目标群体间的遗传距离对填充错误率的影响。三角形标志虚线代表Beagle5.1,圆形标志实线代表Minimac4。不同颜色的标志代表不同水平 A. The influence of reference population size on imputation error rate; B. The influence of target population sites proportion on imputation error rate; C. The influence of genetic distance between reference population and target population on imputation error rate. The dotted lines with a triangle sign represent Beagle5.1, and the solid lines with a round sign represent Minimac4. Different colored signs represent different levels 图 3 不同因素对填充错误率的影响 Fig. 3 The influence of different factors on imputation error rate |
如图 3所示,无论参考群体大小、目标群体位点比例或遗传距离是否发生变化,MAF大小对错误率的影响都是极显著且呈正相关(P < 1×10-4,0.542 < r < 0.973),随MAF的增加,填充错误率也随之增加。这种趋势在参考群体个体数量少、目标群体位点比例低或遗传距离远时更为明显。例如图 3A中,利用Beagle5.1填充,当参考群体大小为100(浅绿色标记虚线)时,MAF由0~0.05区间增至0.45~0.5区间,错误率由2.5%增加到19.8%。再例如图 3B中,利用Minimac4填充,当目标群体位点比例为1%时,随着MAF由0~0.05区间增至0.45~0.5,错误率由1.7%增加到13.6%。
根据以上结果,计算了各因素不同水平下影响错误率变化的变异系数。在Beagle5.1中,参考群体大小、目标位点比例和MAF对错误率影响的变异系数分别为0.537、0.372和0.396。在Minimac4中,目标位点比例和MAF对错误率影响的变异系数为0.476和0.439。这些结果表明,参考群体大小在Beagle5.1的填充中对错误率的影响最大,而Minimac4中影响错误率最主要的因素是目标位点比例,此外, MAF在两种软件中对错误率的影响都占有很高权重。如表 4所示,Beagle5.1和Minimac4填充的错误率范围分别为1.2% < ER < 17.6%和4.6% < ER < 17.5%,且仅当参考群体数量较少,目标群体标记比例较大时,Minimac4的填充错误率才低于Beagle5.1。如果要求基因型填充的效果达到理想状态,即错误率控制在5%以内,利用Beagle5.1填充时,参考群体大小需要达到3 000以上,且目标群体标记比例需达到10%;利用Minimac4填充时需要标记比例达到90%以上。
|
|
表 4 不同水平填充错误率统计信息 Table 4 The statistics of imputation error rate at different levels |
两种软件在不同参考群体大小和目标群体标记比例的情况下,填充1 000个目标个体所需时间如表 5所示,可以发现,Beagle5.1的填充耗时受参考群体大小的影响不大,只随目标群体标记比例的增加而增加。而Minimac4受这两种因素的影响都很明显。在本研究范围内,Beagle5.1只有在标记位点比例为1%且参考群体个体大于1 000,或者标记位点比例为5%且参考群体个体为10 000时速度优于Minimac4,但由于在Beagle5.1中参考群体大小对耗时影响很小,根据趋势可预测随参考群体个体数量不断增加,最终Beagle5.1填充速度会比Minimac4快。
|
|
表 5 不同水平下两种软件的填充耗时 Table 5 Imputation time of two softwares at different levels |
相对于其他经典溯祖模拟软件,msprime具有一些自身独特的优势:其一,它能在整个染色体上直接使用真实的重组模型模拟,而不依靠连续马尔可夫溯祖(sequentially Markov Coalescent, SMC)近似值,以极高的效率模拟出大量的样本,这是其他软件不能做到的;其二,msprime的模拟数据结构是以一种非常规整且方便的树序列(tree sequence)形式展现的,并且拥有强大的Python API接口工具支持后续数据处理[36]。因此,msprime一经公布,便被广泛应用于人类和家畜群体数据模拟研究[37]。
填充准确性和填充错误率这两种评价填充质量的标准各有优缺点,填充准确性的衡量是以位点间的皮尔逊相关系数的平方为基础的,这点与育种值的定义不谋而合,并且准确性随MAF改变的变化很小,相反,填充错误率在很大程度上受到MAF的影响,这就导致了无法确定填充结果是否符合后续工作要求[38]。因此,在将填充结果用于基因组预测时(如基因组选择),填充准确性是一个很好的衡量标准。而当后续研究对位点精确度的要求较高时(如利用GWAS检测罕见突变位点),由于稀有的突变位点填充困难,在填充过程中有较高的比例被校正,导致这些位点的平均相关性较低,计算准确性往往会忽略这些位点的相关性,使他们在分析中被排除[39],此时,以错误率作为衡量标准是更好的选择。
参考群体大小、目标群体位点比例、目标群体与参考群体间的遗传距离远近、最小等位基因频率和填充软件都是影响基因型填充的关键因素。关于在填充过程中如何选择控制这几项因素,在不同条件下应该选择何种策略,还没有系统的报道。目前有很多种填充软件,但依旧在不停更新版本的只有Beagle、Minimac、Impute等少数填充软件,新版本的软件在填充性能和精确性方面较旧版本都有显著提升,这也使得研究较早版本的软件意义不大,因此,本研究选择Beagle和Minimac的最新版本进行试验。本研究表明,在两种填充软件中,不同因素的影响效果不一定相同。在此首先讨论共同点,随着参考群体个体数目的增加,在保持遗传距离较近的情况下,基因型填充的准确性随之增加;此研究结果与Das等[28]和Huang等[40]等之前的结论相符。这是因为,较多的参考群体个体数目能够提供更多的样本单倍型,填充数据与原始数据的相关性更高,使得填充准确性更高。目标群体标记比例(数量)对填充准确性和填充错误率均存在显著影响,随着目标群体标记比例的增加,基因型填充的准确性增加,错误率降低。在Zhang和Druet[35]之前的报道中也有类似结果,这是因为当位点数目增加时,目标单倍型上的标记更多,更容易匹配相关性和一致性高的参考单倍型,使填充准确性更高。随着遗传距离的增加,填充的准确性在不同程度上有降低趋势,而错误率有增加的趋势,这点也与之前的报道相吻合[41],遗传距离的增加可以降低参考单倍型与目标群体的相关性,不能保证参考面板内涵盖所有目标单倍型的所有标记,从而降低填充准确性。MAF是影响填充错误率的一个主要因素,且影响呈正相关,而MAF对填充准确性的影响并不大,这是因为软件在填充过程中首先计算参考单倍型和目标单倍型间的相关性,然后才考虑单倍型间的一致性,所以在对等位基因频率较高的标记填充时,在保持相关性很高的情形下,如果两个基因型间的频率相差不大,就可能无法对该标记进行正确分型[42-43]。
然而,除以上共同点之外,同一因素在两种填充软件间也存在差异。当考虑参考群体大小对填充错误率的影响时,在Minimac4中,参考群体大小并不能显著影响错误率,而在Beagle5.1的填充中参考群体大小的变化对错误率的影响是显著的,这点与Hozé等[44]的报道结果相同,但与Zhang和Druet[35]报道的与SNP位点数量和遗传关系相比,参考群体大小对填充错误率的影响是相对较小的有所不同。导致此差异的原因,应该与软件的填充算法有关,尽管Beagle5.1和Minimac4都是利用HMM中的状态空间简化构造简化的单倍型集来减少计算消耗的,但具体的简化方法和填充方法有所不同。在Beagle5.1中,这种简化方法基于同源相同(identity by descent, IBD)。在进行填充之前,Beagle5.1通过识别参考单倍型间所共享的IBD片段,将所识别的IBD片段整合成一个子集合,如果该子集中包含的参考单倍型与目标单倍型在每个位置都共享最长IBD片段,那么子集可以产生与完整参考单倍型集合相同的填充精度。而后根据目标单倍型信息,将以上单倍型子集继续构造一组目标特定的复合参考单倍型集合,每一条复合参考单倍型都是由参考单倍型部分长短不一的片段组合而成。后将目标单倍型视作HMM中的一条从第一个标记到最后一个标记的不完整路径,然后通过HMM统计该路径每一个未分型标记的后验概率,经过迭代将每一个标记逐步填充完整[33]。以上说明,在利用Beagle5.1填充时,由于参考群体大小或参考群体与目标群体遗传距离的变化会影响IBD片段的计算,使产生的复合参考单倍型集合随之变化,从而影响填充效果。在Minimac4的算法中,简化HMM状态空间的方法是先通过计算将整个基因组划分为相连的基因组区间段,在每一区间段上都有唯一的参考单倍型,并且只在该单倍型上进行迭代,然后通过逆映射函数精确地重建状态空间,以此来达到简化状态空间的目的,尽管这种简化空间没有减少参考标记位点的数量,但固定了影响效率的因素。在填充时,只针对每一连续基因组区域上的单倍型进行匹配,对该区段目标单倍型标记缺失的部分同时进行填充,再将每个段落连接成完整的染色体片段[34]。以上说明,在本研究中,利用Minimac4填充时,可能由于参考标记数目是固定的,所以基因组分割成的连续区间长度也相对固定,参考群体大小只能水平地影响每一区间内参考单倍型的数目,无法垂直调整单条染色体上参考单倍型的长度和数目,所以目标单倍型只能分开匹配或只匹配参考单倍型的一部分,而当目标位点数目不变时,其匹配到的参考单倍型是固定的。这导致在填充时,随着参考群体个体数目增加,填充的准确性(相关性)增加,错误率几乎没有变化,而目标群体标记数量的增加可以明显改善这种情况。
影响填充时间的因素是多种多样的。如在Beagle5.1中,填充速度主要取决于复合参考单倍型集的计算,同时复合参考单倍型集的计算取决于目标位点数量,只有当目标位点数目变化时,复合单倍型集内的参考单倍型才会发生改变并影响填充速度,所以主要的影响因素是目标群体位点数目,而参考群体个体数目的变化并不会显著影响Beagle5.1的填充速度。在Minimac4中,由于没有减少参考单倍型数目,所以参考群体大小和目标群体标记数目都能显著影响填充耗时。除了以上外部因素外,软件的自身算法升级优化是影响耗时最主要的因素,随着软件版本的更新,填充速度会得到极大提升,使用最新版本的填充软件是很好的选择。
4 结论随着基因型填充技术的广泛应用,需要针对不同目的选择不同的填充策略。对1 000个目标样本来讲:1)如果要将填充的结果用于基因组预测,并与真实数据相关性达到理想(r2>0.9)状态,利用Beagle5.1填充需要至少3 000个参考样本,且目标群体标记比例达到10%;利用Minimac4填充需要达到10 000以上的参考样本,且目标群体标记比例非常高(90%)。2)如果填充结果对标记的正确率要求较高(如GWAS),并达到理想状态(ER < 5%), 则利用Beagle5.1需要至少3 000个参考群体,且目标群体标记比例达到5%;利用Minimac4填充时,参考群体个体数目需要100以上,且目标群体标记比例达到90%。总体来讲Beagle5.1更适合参考群体个体数目较多,目标群体位点数目(比例)较低的填充中,而Minimac4更适合参考群体个体数目较少,目标群体位点数目(比例)较高的填充中。当考虑填充效果相近的情况下,Beagle5.1对影响填充效果的因素标准的要求比Minimac4低。以上结论为基因型填充的标准提供了参考依据。
| [1] | ZHANG H, WANG Z P, WANG S Z, et al. Progress of genome wide association study in domestic animals[J]. J Anim Sci Biotechnol, 2012, 3(1): 26. |
| [2] | HAYES B, GODDARD M. Genome-wide association and genomic selection in animal breeding[J]. Genome, 2010, 53(11): 876–883. DOI: 10.1139/G10-076 |
| [3] | LACHANCE J, TISHKOFF S A. SNP ascertainment bias in population genetic analyses:why it is important, and how to correct it[J]. Bioessays, 2013, 35(9): 780–786. DOI: 10.1002/bies.201300014 |
| [4] | DRUET T, MACLEOD I M, HAYES B J. Toward genomic prediction from whole-genome sequence data:impact of sequencing design on genotype imputation and accuracy of predictions[J]. Heredity, 2014, 112(1): 39–47. DOI: 10.1038/hdy.2013.13 |
| [5] | MEUWISSEN T, GODDARD M. Accurate prediction of genetic values for complex traits by whole-genome resequencing[J]. Genetics, 2010, 185(2): 623–631. |
| [6] | WEISSENKAMPEN J D, JIANG Y, ECKERT S, et al. Methods for the analysis and interpretation for rare variants associated with complex traits[J]. Curr Protoc Hum Genet, 2019, 101(1): e83. DOI: 10.1002/cphg.83 |
| [7] | LI Y, WILLER C, SANNA S, et al. Genotype imputation[J]. Annu Rev Genomics Hum Genet, 2009, 10(1): 387–406. DOI: 10.1146/annurev.genom.9.081307.164242 |
| [8] | MARCHINI J, HOWIE B. Genotype imputation for genome-wide association studies[J]. Nat Rev Genet, 2010, 11(7): 499–511. DOI: 10.1038/nrg2796 |
| [9] |
何桑, 丁向东, 张勤. 基因型填充方法介绍及比较[J]. 中国畜牧杂志, 2013, 49(23): 95–100.
HE S, DING X D, ZHANG Q. Comparison of different genotype imputation methods[J]. Chinese Journal of Animal Science, 2013, 49(23): 95–100. (in Chinese) |
| [10] | MAHAJAN A, TALIUN D, THURNER M, et al. Fine-mapping type 2 diabetes loci to single-variant resolution using high-density imputation and islet-specific epigenome maps[J]. Nat Genet, 2018, 50(11): 1505–1513. |
| [11] | ORHO-MELANDER M, MELANDER O, GUIDUCCI C, et al. Common missense variant in the glucokinase regulatory protein gene is associated with increased plasma triglyceride and C-reactive protein but lower fasting glucose concentrations[J]. Diabetes, 2008, 57(11): 3112–3121. DOI: 10.2337/db08-0516 |
| [12] | HUANG X H, YANG S H, GONG J Y, et al. Genomic analysis of hybrid rice varieties reveals numerous superior alleles that contribute to heterosis[J]. Nat Commun, 2015, 6(1): 6258. |
| [13] | IBEAGHA-AWEMU E M, PETERS S O, AKWANJI K A, et al. High density genome wide genotyping-by-sequencing and association identifies common and low frequency SNPs, and novel candidate genes influencing cow milk traits[J]. Sci Rep, 2016, 6(1): 31109. |
| [14] | ALILOO H, MRODE R, OKEYO A M, et al. The feasibility of using low-density marker panels for genotype imputation and genomic prediction of crossbred dairy cattle of East Africa[J]. J Dairy Sci, 2018, 101(10): 9108–9127. DOI: 10.3168/jds.2018-14621 |
| [15] | GROSSI D A, BRITO L F, JAFARIKIA M, et al. Genotype imputation from various low-density SNP panels and its impact on accuracy of genomic breeding values in pigs[J]. Animal, 2018, 12(11): 2235–2245. DOI: 10.1017/S175173111800085X |
| [16] | ZHANG C Y, KEMP R A, STOTHARD P, et al. Genomic evaluation of feed efficiency component traits in Duroc pigs using 80K, 650K and whole-genome sequence variants[J]. Genet Sel Evol, 2018, 50(1): 14. |
| [17] | RAOUL J, SWAN A A, ELSEN J M. Using a very low-density SNP panel for genomic selection in a breeding program for sheep[J]. Genet Sel Evol, 2017, 49(1): 76. |
| [18] | YE S P, YUAN X L, LIN X R, et al. Imputation from SNP chip to sequence:a case study in a Chinese indigenous chicken population[J]. J Anim Sci Biotechnol, 2018, 9(1): 30. |
| [19] | DENG M T, ZHU F, YANG Y Z, et al. Genome-wide association study reveals novel loci associated with body size and carcass yields in Pekin ducks[J]. BMC Genomics, 2019, 20(1): 1. DOI: 10.1186/s12864-018-5379-1 |
| [20] | BROWNING B L, BROWNING S R. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals[J]. Am J Hum Genet, 2009, 84(2): 210–223. |
| [21] | HEIDARITABAR M, CALUS M P L, VEREIJKEN A, et al. Accuracy of imputation using the most common sires as reference population in layer chickens[J]. BMC Genetics, 2015, 16(1): 101. DOI: 10.1186/s12863-015-0253-5 |
| [22] | ROSHYARA N R, SCHOLZ M. Impact of genetic similarity on imputation accuracy[J]. BMC Genetics, 2015, 16(1): 90. DOI: 10.1186/s12863-015-0248-2 |
| [23] | NHO K, SHEN L, KIM S, et al.The effect of reference panels and software tools on genotype imputation[C]//Proceedings of the AMIA Annual Symposium Proceedings.American Medical Informatics Association, 2011: 1013-1018. https://www.researchgate.net/publication/51921276_The_Effect_of_Reference_Panels_and_Software_Tools_on_Genotype_Imputation |
| [24] | KELLEHER J, ETHERIDGE A M, MCVEAN G. Efficient coalescent simulation and genealogical analysis for large sample sizes[J]. PLoS Comput Biol, 2016, 12(5): e1004842. DOI: 10.1371/journal.pcbi.1004842 |
| [25] | GIUFFRA E, KIJAS J M H, AMARGER V, et al. The origin of the domestic pig:independent domestication and subsequent introgression[J]. Genetics, 2000, 154(4): 1785–1791. |
| [26] | KIM K I, LEE J H, LI K, et al. Phylogenetic relationships of Asian and European pig breeds determined by mitochondrial DNA D-loop sequence polymorphism[J]. Anim Genet, 2002, 33(1): 19–25. |
| [27] | FRANTZ L A F, SCHRAIBER J G, MADSEN O, et al. Evidence of long-term gene flow and selection during domestication from analyses of Eurasian wild and domestic pig genomes[J]. Nat Genet, 2015, 47(10): 1141–1148. DOI: 10.1038/ng.3394 |
| [28] | DAS S, ABECASIS G R, BROWNING B L. Genotype imputation from large reference panels[J]. Annu Rev Genomics Hum Genet, 2018, 19(1): 73–96. DOI: 10.1146/annurev-genom-083117-021602 |
| [29] | DELANEAU O, ZAGURY J F, MARCHINI J. Improved whole-chromosome phasing for disease and population genetic studies[J]. Nat Methods, 2013, 10(1): 5–6. |
| [30] | LOH P R, DANECEK P, PALAMARA P F, et al. Reference-based phasing using the Haplotype Reference Consortium panel[J]. Nat Genet, 2016, 48(11): 1443–1448. DOI: 10.1038/ng.3679 |
| [31] | HOWIE B, MARCHINI J, STEPHENS M. Genotype imputation with thousands of genomes[J]. G3 (Bethesda), 2011, 1(6): 457–470. DOI: 10.1534/g3.111.001198 |
| [32] | DRUET T, GEORGES M. A hidden Markov model combining linkage and linkage disequilibrium information for haplotype reconstruction and quantitative trait locus fine mapping[J]. Genetics, 2010, 184(3): 789–798. DOI: 10.1534/genetics.109.108431 |
| [33] | BROWNING B L, ZHOU Y, BROWNING S R. A one-penny imputed genome from next-generation reference panels[J]. Am J Hum Genet, 2018, 103(3): 338–348. |
| [34] | DAS S, FORER L, SCHÖNHERR S, et al. Next-generation genotype imputation service and methods[J]. Nat Genet, 2016, 48(10): 1284–1287. DOI: 10.1038/ng.3656 |
| [35] | ZHANG Z Y, DRUET T. Marker imputation with low-density marker panels in Dutch Holstein cattle[J]. J Dairy Sci, 2010, 93(11): 5487–5494. DOI: 10.3168/jds.2010-3501 |
| [36] | KELLEHER J, LOHSE K.Coalescent Simulation with msprime[M]//DUTHEIL J Y.Statistical Population Genomics.New York, NY: Humana, 2020: 191-230. |
| [37] | SANCHEZ T, CURY J, CHARPIAT G, et al.Deep learning for population size history inference: design, comparison and combination with approximate Bayesian computation[J/OL].bioRxiv, 2020, doi: 10.1101/2020.01.20.910539. |
| [38] | CALUS M P L, BOUWMAN A C, HICKEY J M, et al. Evaluation of measures of correctness of genotype imputation in the context of genomic prediction:a review of livestock applications[J]. Animal, 2014, 8(11): 1743–1753. DOI: 10.1017/S1751731114001803 |
| [39] | POOK T, MAYER M, GEIBEL J, et al. Improving imputation quality in BEAGLE for crop and livestock data[J]. G3 (Bethesda), 2020, 10(1): 177–188. DOI: 10.1534/g3.119.400798 |
| [40] | HUANG L, LI Y, SINGLETON A B, et al. Genotype-imputation accuracy across worldwide human populations[J]. Am J Hum Genet, 2009, 84(2): 235–250. |
| [41] | CARVALHEIRO R, BOISON S A, NEVES H H R, et al. Accuracy of genotype imputation in Nelore cattle[J]. Genet Sel Evol, 2014, 46(1): 69. |
| [42] | OLIVEIRA JÚNIOR G A, CHUD T C S, VENTURA R V, et al. Genotype imputation in a tropical crossbred dairy cattle population[J]. J Dairy Sci, 2017, 100(12): 9623–9634. DOI: 10.3168/jds.2017-12732 |
| [43] | HUANG L, WANG C L, ROSENBERG N A. The relationship between imputation error and statistical power in genetic association studies in diverse populations[J]. Am J Hum Genet, 2009, 85(5): 692–698. DOI: 10.1016/j.ajhg.2009.09.017 |
| [44] | HOZÉ C, FOUILLOUX M N, VENOT E, et al. High-density marker imputation accuracy in sixteen French cattle breeds[J]. Genet Sel Evol, 2013, 45(1): 33. |



