在经历了20世纪最后十年的快速增长以及互联网经济带来的广泛繁荣之后, 因为互联网经济泡沫的破灭导致全球很多发达的经济体陷入了经济衰退的态势。为缓解经济下行压力, 降低利率刺激经济成为了许多中央银行的选择。从货币政策实践的历史角度来看, 降低利率的货币政策获得了此前货币当局抑制高水平通货膨胀成功经验的支持, 符合他们的历史经验。然而, 过度的流动性鼓励了银行风险承担, 由此带来的金融不稳定并没有引起足够的注意。全球大部分货币当局将严格的通胀目标作为他们促进经济增长的贡献, 人们普遍认为金融创新能够使得风险分配更有效率, 并认为金融创新是加强金融体系弹性的重要组成部分, 很多国家的货币当局像美联储那样鼓励金融市场的参与者相信它的不对称的货币政策, 使得市场参与者产生了更多承担金融风险的狂热[1]。
然而, 2007年至2009年的金融危机表明, 关注于价格稳定的货币政策并没有使得经济免于金融不稳定。尽管很难将危机发生的主要原因归咎于货币政策, 但客观上全球流动性的泛滥确实是其中的一个较为突出的诱因, 相对宽松的货币政策即环境催生了包括房地产在内的大量资产价格泡沫的产生, 直接抬高并导致金融机构承担更大的杠杆以及相应风险。货币政策促进了银行承担过度风险, 这在一定程度上导致了金融体系风险的积聚, 从而对金融和经济的稳定产生影响[2]。
基于对2008年经济危机以来全球主要经济体及很多大型金融机构的研究作为背景, 很多研究者开始侧重如下方面的研究, 也产生了很多新的研究课题:货币政策的转向对银行业金融机构承担风险的路径和意愿是否有影响?是否应将金融稳定纳入货币政策目标?货币政策框架下的金融摩擦如何定义和解决?价格和金融稳定如何权衡和选择取舍?单一的政策工具是否能够同时达到以上两个目标?这些是国内外学术界共同面对的问题。本文通过因子增广向量自回归模型, 基于中国2000—2012年宏—微观非平稳面板的季度数据, 考察了中国货币政策传导风险承担渠道的存在性, 对上述问题进行了初步的探索。
一、文献综述货币政策传导的风险承担渠道是在基于大规模爆发的金融危机的实际基础上提出来的, 同时在一定程度上这个课题也是从传统货币政策传导渠道伴生出来的, 它丰富了有关金融摩擦的理论, 加深了对货币政策和金融稳定政策之间关系的理解。在对现存文献的梳理中, 我们发现:
(1) 大部分文献研究的结论表明, 货币政策传导的风险承担渠道是存在的, 但也有少数研究认为没有足够有力的证据显示货币政策立场对金融市场参与者风险承担有影响。货币政策与风险承担的关系是不确定的, 例如, 较低的政策利率可以增加银行资产的价值, 增加内部权益股份(the share of inside equity), 因而, 减少银行和存款人之间的道德风险(即降低风险承担)。
(2) 不对称性。首先, 作用时间的不对称性, 即货币政策利率与风险承担短期正相关、中长期负相关。短期内银行风险会伴随着利率的下降而降低, 但是在长期内则相反。其次, 作用对象的不对称性:①增量负相关、存量正相关。②不同类型的银行反应不同, 这是相对显著的一个观察点, 就是小型本地银行增加风险敞口, 外国银行减少风险敞口, 大型本国银行未改变风险敞口。
(3) 从现存的文献中, 我们可以看出, 这种渠道会受到宏观经济状况、银行体系健康程度、银行资本充足情况和银行的规模等方面的影响。此外, 从现有的研究成果来看, 风险过度承担和低利率之间的关联关系也会受到其他因素的影响, 比如监管缺陷和投资者心理, 银行的流动性、资本水平和市场竞争力、银行规模、宏观经济状况等因素的影响。
二、模型构建与数据说明在研究货币政策传导的风险承担渠道中, 我们要分清该渠道同标准的“金融加速器”机制的区别, 后者是通过企业和家庭的金融摩擦对外生冲击加以放大或者传播。
“金融加速器”的作用基础是通过借款人的净值(净财富):宽松的货币政策环境使得相应的评估标准发生了改变, 对个人净值信用产生较大的正向增加, 也会在很大程度上增加借款人抵押品的价值, 从而从另外一个层面上提升了他们整体的信用水平。在这种宽松和评估评价借款人信用的政策及环境背景下, 银行更愿意去放松信贷业务的约束、增加对他们对用户的贷款额度, 这样周而复始导致银行杠杆率螺旋式提升。因此, “金融加速器”强调了一个由借款人的金融摩擦而产生的信贷驱动放大机制。相反, 风险承担渠道关注于有关贷款人——银行金融摩擦的放大机制[3]。
为了控制借款人净值的影响, 我们在模型中加入一系列宏观经济控制变量, 如房地产价格等资产价格的变化, 将这些资产价格以他们历史长期的平均值加以矮化(demean), 对于一个给定的银行规避风险水平, 这些变量意味着抵押品价值的改变, 用以捕获资产价格变动对银行风险头寸的影响。加入宏观经济控制变量的另一个目的是控制一般经济状况和对未来经济活动的预期对银行风险产生影响。此外, 为了控制上文提到的银行的流动性、规模、资本水平等银行特征变量的影响, 我们将在模型中加入表示银行特征的控制变量。
本文基于Bernanke, Boivin and Eliasz(2005)(BBE)提出的因子增广型向量自回归模型, 来考察我国货币政策传导的风险承担渠道。假定N×1维银行变量Xt符合下面的近似动态因子模型(Stock and Watson, 2002;Bai and Ng, 2002):
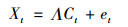
|
(1) |
其中, Λ是N×K维因子载荷矩阵, Ct表示不可观测的K×1维公共因子, et表示具有零均值N×1维的特殊因子, 弱序列相关, 但与公共因子Ct不相关, 即, 具有近似因子结构。假定公共因子的维数远远小于银行指标的维数, 即, N≫K。同时, 假定Ct由宏观经济因子Gt和银行因子Ht两部分组成, 其中Gt是从中国一系列宏观经济指标集Yt中提取出来的中国宏观经济因子。因此:
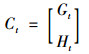
|
(2) |
在这个结构下, Gt和Ht共同构成了Xt波动的主要动因, 全面反映了银行变量的基本性质。此外, Xt不仅仅依赖于公共因子的当前值, Ct的任意期滞后也可能成为它们波动的原因。这些无法观测的因子分别反映了宏观经济和银行所处的状态, 如宏观经济中的一般物价水平、潜在产出,等等。然而, 这些状态很难被少数几个时间序列所反映, 但可以通过大量的变量加以刻画。
这些基本状态因素的动态变化可以用一个VAR模型来表示:
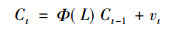
|
(3) |
其中, vt是误差项, 具有i.i.d.、零均值的结构。
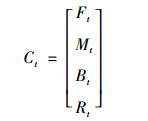
我们将可观测到的货币政策工具作为中国的基本经济因素之一, 并将其加入到宏观经济因子向量之中。从我国货币政策实践来看, 我国在1998年改革了以控制信贷规模为主的货币政策调控方式, 将货币供应量作为唯一的中介目标, 又由于我国没有实现利率市场化, 因此, 本文将M1的同比增长率作为货币政策的代理变量。同时, 我们将银行风险因子(表示其风险承担意愿)作为银行因子之一, 将其加入到银行因子向量之中。这样, 上面(2)式改写为:
|
(4) |
其中, [FtMt]′=Gt, Ft表示潜在的、不可观测的中国宏观经济状态因子, Mt是可以观测到的货币政策工具的代理变量, [BtRt]=Ht, Bt表示银行状态因子, Rt是银行风险因子。
实际上, 上面的理论模型是一个近似动态因子模型。通过公式(1)和(2), 将大规模可以观测到的宏观经济指标和银行指标同少量不可观测的因子(宏观因子、银行因子)联系起来。而这些因子的动态变化由公式(3)反映。在BBE的论文中, 将不可观测的因子Ct解释为宏观经济模型中的一些理论上的概念或者微观中不易测量的变量, 例如, 开放经济动态一般均衡模型中的通货膨胀、潜在产出,等等。他们认为这些变量均包括在Ct之中, 其动态变化能够被非限制性VAR模型(3)近似地表示。如果这些变量能够被完美地观测到, 那么系统(1)—(3)将退化为一个标准的VAR模型, 并且可以直接估计, 将不再需要大规模的指标集Xt然而, Bernanke et al.(2005)认为这些变量并不能完美地被观测到:首先, 经济指标有一定的测量误差; 其次, 某些模型中关键的经济变量是不可能观测到的。例如, “潜在产出”经常是货币模型中决定性变量, 但并不能直接被测量到。他们认为, 通过利用大规模数据集, 能够将影响经济波动的一些最重要的基本因素提取出来, 尽管单个因子并不能准确地表达为某个具体的经济概念, 但是公共因子的集合ct可以构造出一个包含这些所有相关经济因素的线性组合。[4]。
FAVAR分析框架有两个明显优势, 首先, 从大规模数据集中提取出因子, 用以反映中国经济状态和银行状态的有代表性子空间, 这样我们不需要将分析仅仅局限于经济增长等几个有限的变量; 其次, 正如Bernanke et al.(2005)指出的, 同标准的VAR模型相比, 这个框架能够更好地识别货币政策冲击, 因为这一框架涵盖了大规模信息集, 并且不必准确地度量价格、实际产出等变量, 仅仅将其作为潜在的公共因子即可。此外, 这一框架还能够给出数据集合中所有经济变量的脉冲响应函数。因此, FAVAR框架是目前解决这类问题最适用的方法。
此外, 为了考察不同类型的银行风险承担意愿对货币政策冲击的反应, 本文将对比全部银行、四大国有银行、其他上市银行的情况。本文采用非平衡面板数据来进行实证分析①, 样本期为2000年第1季度到2012年第2季度, 数据包括了我国63种宏观经济数据和16家样本银行②的微观数据。数据来源于IMF的IFS(International Financial Statistics)、EIU Country Data、中经网数据库、Bankscope数据库和历年《中国金融年鉴》。这些变量较为全面和准确地描述了我国年度的宏观经济状态和银行状态。为了进一步增强模型数据的严谨性和科学性, 在对这些数据进行计量回归之前, 先对某些变量进行了一阶差分、对数化、对数的一阶差分处理。
① 由于我国银行的季度数据存在缺失情况, 即, 样本数据是非平衡的, 因此, 本文结合EM算法来估计FAVAR模型, 相关技术细节参见Stock and Watson(2002)附录A。
② 16家样本银行包括中国工商银行、中国农业银行、中国银行、中国建设银行、交通银行、招商银行、中信银行、华夏银行、民生银行、光大银行、平安银行、上海浦发银行、兴业银行、南京银行、宁波银行、北京银行。
根据前文的分析, 货币政策传导的风险承担渠道主要是通过改变银行风险承担意愿或者说是偏好来最终作用于实体经济并影响金融稳定。此外, 从我国银行业长期以来业务单一、贷款是银行最主要的风险的实际情况出发, 本文用非贷款损失准备占贷款总额之比的变化(Risk1)作为风险承担意愿的代理变量。同时, 为了结论的稳健性, 本文参考Delis and Kouretas(2010)的思路, 将银行风险资产占总资产比率的变化(Risk2)作为另一个代理变量, 其中, 风险资产是所有价值会跟随货币市场或信贷市场波动的资产, 包括银行总资产中除去现金、存放中央银行款项以及存放同业的剩余部分[5]。显然, 以上两种比率的正向变动越大, 说明银行有更强的风险承担的意愿。尽管这两个代理变量并不能够科学、完美地刻画银行风险承担的意愿, 但却体现了风险承担渠道中银行主动的风险选择的本质。
如何确定公共因子的个数和VAR模型的滞后阶数在整个模型中是一个十分重要的步骤。公共因子被看作是引起相关对应变量波动的冲击的变量。在很多的实际研究和文献中, 经济波动是由于少数几个冲击引起的作为较为通用的假设被普遍采纳和接受[6]。但在Bai-Ng(2007)的论文中指出这并不是一个必然符合实际的假设。因此, 根据他们论文中所建立的准则, 本文最后选定5个宏观因子和5个银行因子(包含货币政策的代理变量和银行风险承担意愿的代理变量)。此外, 鉴于数据样本量的大小, 同时考虑到VAR模型的稳定性, 滞后阶数为1是比较恰当的选择。此外, 还需要考虑货币政策的内生性问题。我们认为, 在本文所研究的样本期间内, 我国中央银行在它的货币政策决策中并没有系统地考虑银行风险承担意愿。也就是说, 当中央银行对银行风险加以考虑, 是诉诸于其他工具, 例如一些微观层面的监管, 而不是货币政策。
三、实证结果分析在上面的计量框架下, 本文假定银行风险因子不会在冲击当期对货币政策工具的变化予以反应, 研究表明, 银行系统的风险承担意愿随着扩张性的货币政策的开展而相应增强了, 但是, 不同类型的银行对于冲击的响应确有着截然不同的表现。首先, 我们先看第1种风险因子的响应结果, 对于全部银行和四大银行, 在响应初期对货币政策冲击有正向响应, 并在冲击的大约第3期达到最大值, 随后的响应值迅速趋向于接近于零的数值。不同的是, 四大银行对冲击的响应幅度要远远大于全部银行, 而对于其他上市银行, 在期初的时候整体风险承担意愿是下降的, 这种反应与这些银行自身的规模和经营策略以及他们对宏观经济的判断有关。此外, 对冲击响应的幅度远小于四大银行和全部银行的平均水平。其次, 从两种风险因子获得的响应结果来看, 各类型银行在冲击响应的趋势性、方向上几乎没有本质的区别, 只是第2种风险因子的响应幅度小于第1种风险因子的响应幅度, 可以认为结论具有稳健性。第三, 从对冲击响应的持续期来看, 在大约冲击的5—6期以后, 冲击的影响很微弱, 但影响并没有完全消失, 可见影响具有微弱的持续性。
四、结论通过对我国货币政策传导的风险承担渠道存在性的实证分析, 我们发现我国存在货币政策传导的风险承担渠道, 这一结论可以帮助我们从风险承担的角度来认识货币政策传导机制及其效率, 使我们能够更深层次地理解货币政策与金融稳定政策之间的关系。通过本文的实证分析可知, 货币政策并不是完全中性的结论在我国可能更加成立。同时, 最重要的是, 货币政策传导的风险承担渠道的存在表明我国的货币当局负有宏观审慎监管系统性风险的责任。
| [1] |
TOBIAS A, MOENCH E, SHIN H S. Macro Risk Premiums and Intermediary Balance Sheet Quantities[M]. Federal Reserve Bank of New York Staff Report, 2010.
|
| [2] |
张强, 张宝. 货币政策传导的风险承担渠道研究进展[J]. 经济学动态, 2011, (10). |
| [3] |
张雪兰, 何德旭. 货币政策立场与银行风险承担[J]. 经济研究, 2012, (5). |
| [4] |
BERNANKE B, BLINDER A S. Is it Money or Credit, or Both or Neither? Credit, Money and Aggregate Demand[J]. American Economic Review, 1988, (2). |
| [5] |
BARRELL R, DAVIS E P, KARIM D, et al. Bank regulation, property prices and early warning systems for banking crises in OECD countries[J]. Journal of Banking and Finance, 2010, (34). |
| [6] |
BAI J, NG S. Determining the number of factors in approximate factor models[J]. Econometrica, 2002, (1). |
 2017, Vol. 47
2017, Vol. 47