2. 西安市汽车维修行业管理处,陕西 西安 710054
2. Xi′an Automobile Maintenance Industry Management Office, Xi′an 710054, China
汽车稳定性控制(Vehicle stability control, VSC)是通过调节车辆驱动轮纵向力, 在转向行驶或受外界干扰时, 实现良好的操纵稳定性的一种主动安全控制系统[1]。汽车稳定性控制方法主要包括:四轮转向控制(4 Wheel steering, 4WS), 主动前轮转向控制(Adaptive front-wheel system, AFS), 直接横摆力矩控制(Direct yaw-moment control, DYC)等[2]。目前, 直接横摆力矩控制具有控制精度高、响应速度快、控制方式容易实现等优势, 已成为汽车稳定性控制的主要方式[3]。
电动汽车的操纵稳定性控制主要包括3个方面内容:对车辆状态参数的估计、对需求横摆力矩的决策以及对横摆力矩的分配[4]。Nagai等人[5]研究了主动前轮转向控制和直接横摆力矩控制联合控制方式对汽车操纵稳定性控制的影响; Ford公司的Lu等人[6]提出了一种基于控制算法实现的防侧翻电子稳定性控制系统(Electronic stability control, ESC); Justin等人[7]提出了通过控制饱和平衡来增强车辆稳定性的控制方法; 东南大学陈南教授等[8]提出了基于集成DYC控制和主动四轮转向的控制方法; 合肥工业大学的陈无畏等人[9]基于状态识别的协调控制器, 对悬架系统采用PID控制方法, 对转向系统运用滑模变结构理论进行控制, 对制动系统采用变滑移率逻辑门限值理论进行控制, 在此基础上实现了对车辆的操纵稳定性以及平顺性的协调控制。
通过以上研究现状分析可以看出, 国内外在电动汽车操纵稳定性控制技术的算法、控制策略及方法、驾驶员意图识别、路面识别等方面均有较多的研究。但是, 对于双电机驱动电动汽车, 特别是FSAE纯电动赛车的操纵稳定性, 相关研究还比较少, 针对纯电动赛车操纵稳定性的具体建模、参数的实时估测及稳定性控制策略的研究分析更是比较少。
本文提出以FSAE纯电动赛车为平台, 以车辆质心侧偏角和横摆角速度作为控制目标, 基于PID模糊逻辑联合控制的车辆操纵稳定性控制策略。
1 车辆动力学模型为了兼顾车辆稳定性控制策略的准确性和实时性, 本文建立了七自由度非线性车辆动力学模型, 分别用于车辆直接横摆力矩控制。
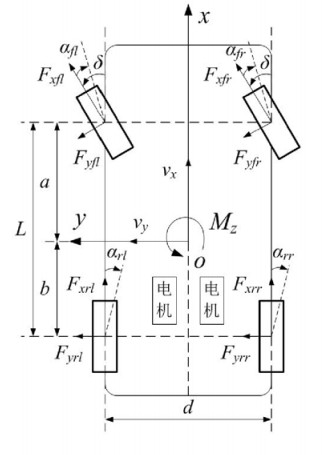
1.1 非线性七自由度整车模型图 1为七自由度车辆动力学模型, 包括汽车纵向、侧向、横摆运动及4个车轮的旋转运动, 忽略汽车的俯仰、侧倾和垂直运动。两电动机布置在后轮, 分别独立给两个后轮输出扭矩。
|
图 1 七自由度整车模型示意图 Fig. 1 7-DOF vehicle system dynamic model |
七自由度整车模型的纵向、侧向、横摆和车轮旋转运动的运动方程为[10]
| $ \begin{array}{l} {F_x} = \left( {{F_{xfl}} + {F_{xfr}}} \right)\cos \delta - \left( {{F_{yfl}} + {F_{yfr}}} \right)\sin \delta + \\ {F_{xrl}} + {F_{xrr}}, \end{array} $ | (1) |
| $ \begin{array}{l} {F_y} = \left( {{F_{xfl}} + {F_{xfr}}} \right)\sin \delta + \left( {{F_{yfl}} + {F_{yfr}}} \right)\cos \delta + {F_{yrl}} + \\ {F_{yrr}}, \end{array} $ | (2) |
| $ \begin{array}{l} {M_z} = a\left( {{F_{xfl}} + {F_{xfr}}} \right)\sin \delta + a\left( {{F_{yfl}} + {F_{yfr}}} \right)\cos \delta - \\ b\left( {{F_{yrl}} + {F_{yrr}}} \right) + \frac{d}{2}\left( {{F_{xfr}} - {F_{xfl}}} \right)\cos \delta + \\ \frac{d}{2}\left( {{F_{yfl}} - {F_{yfr}}} \right)\sin \delta + \frac{d}{2}\left( {{F_{xrr}} - {F_{xrl}}} \right), \end{array} $ | (3) |
| $ {J_{ij}}{{\dot \omega }_{ij}} = {\mathit{\boldsymbol{T}}_{dij}} - {\mathit{\boldsymbol{T}}_{bij}} - {F_{xij}}{R_r}。$ | (4) |
式中, d为轮距, Fxij,Fyij为车轮的纵向力和侧向力, Tdij,Tbij为车轮的驱动力矩和制动力矩, Jij为车轮的转动惯量, ωij为车轮转动的角速度(ij=fl,fr,rl,rr,分别代表左前轮、右前轮、左后轮、右后轮), Rr为车轮滚动半径。
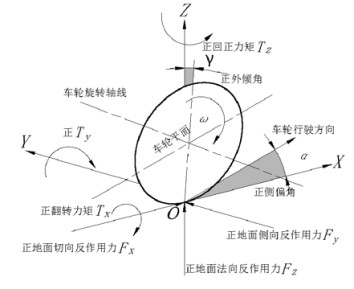
1.2 轮胎模型考虑到轮胎模型对整车模型的重要性,本文选用Dugoff轮胎模型, 该模型能依据轮胎和地面接触区域的变形得到其纵向力和侧向力随着纵向滑移率的变化规律, 能够很好地描述轮胎的受力关系。图 2为轮胎坐标系以及地面作用于轮胎的力和力矩[3]。
|
图 2 轮胎坐标系 Fig. 2 Coordinate system of tyre |
Dugoff轮胎模型数学描述如下:
| $ {F_{xij}} = {C_X}\frac{{{\lambda _{ij}}}}{{1 + {\lambda _{ij}}}}f\left( S \right), $ | (5) |
| $ {F_{yij}} = {C_Y}\frac{{\tan {\alpha _{ij}}}}{{1 + {\lambda _{ij}}}}f\left( S \right), $ | (6) |
| $ f\left( S \right) = \left\{ \begin{array}{l} \left( {2 - S} \right)S,S \le 1\\ 1,S > 1 \end{array} \right. $ | (7) |
| $ S = \frac{{\mu {F_{zij}}\left( {1 + {\lambda _{ij}}} \right)}}{{2\sqrt {{{\left( {{C_X}{\lambda _{ij}}} \right)}^2} + {{\left( {{C_Y}\tan {\alpha _{ij}}} \right)}^2}} }}。$ | (8) |
其中, Fzij为轮胎所受到的垂直载荷, CX和CY分别为轮胎的纵向刚度和侧向刚度, μ为路面附着系数, α为轮胎侧偏角,
由轮胎模型分析可知, 其垂直载荷对侧向力和纵向力有较大的影响, 而车轮的垂直动载荷随汽车行驶工况而变化, 因此在研究轮胎模型时, 必须考虑垂直载荷的变化。车轮的垂直载荷为[12]
| $ {F_{zfj}} = \frac{{mgb}}{{2L}} - \frac{{m{a_x}{h_g}}}{{2L}} \mp \frac{{m{a_y}b{h_g}}}{{Ld}}, $ | (9) |
| $ {F_{zrj}} = \frac{{mga}}{{2L}} + \frac{{m{a_x}{h_g}}}{{2L}} \mp \frac{{m{a_y}a{h_g}}}{{Ld}}。$ | (10) |
其中,Fzfj和Fzrj分别为两个前轮和后轮的垂直载荷,ax和ay分别为车辆质心处的纵向加速度和侧向加速度, hg为质心距离地面的高度。
车辆运行过程中, 各个车轮的侧偏角为
| $ {\alpha _{fj}} = \arctan \frac{{v + a{\omega _{\rm{r}}}}}{{v \mp 0.5d{\omega _{\rm{r}}}}} - \delta , $ | (11) |
| $ {\alpha _{rj}} = \arctan \frac{{v - b{\omega _{\rm{r}}}}}{{v \mp 0.5d{\omega _{\rm{r}}}}}。$ | (12) |
其中,αfj和αrj分别为两个前轮和后轮的侧偏角,vx和vy分别为车辆质心o处的纵向车速和侧向车速。
在汽车侧向动力特性的影响下, 各车轮轮心纵向速度可表示为
| $ {v_{xfj}} = {v_x} \mp \frac{d}{2}{\omega _{\rm{r}}}\cos \delta + \left( {{v_y} + a{\omega _{\rm{r}}}} \right)\sin \delta , $ | (13) |
| $ {v_{yfj}} = {v_x} \mp \frac{d}{2}{\omega _{\rm{r}}}\sin \delta + \left( {{v_y} + a{\omega _{\rm{r}}}} \right)\cos \delta , $ | (14) |
| $ {v_{xrj}} = {v_x} \mp \frac{d}{2}{\omega _{\rm{r}}}, $ | (15) |
| $ {v_{yrj}} = {v_y} - b{\omega _{\rm{r}}}, $ | (16) |
式(13)~(16)中, vxij和vyij分别为车轮轮心的纵向速度和侧向速度。
1.3 驱动电机模型本文的研究平台FSAE纯电动赛车为双电机后轮独立驱动, 采用ENSTROJ公司生产的永磁同步电机, 电机的主要参数如表 1所示。
|
|
表 1 电机主要参数 Tab. 1 Motor parameters |
电机的输出力矩为
| $ \mathit{\boldsymbol{T}} = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_{\rm{e}}},n \le {n_{\rm{e}}}}\\ {9\;550{P_{\rm{e}}}/n,n > {n_{\rm{e}}}} \end{array}} \right. $ | (17) |
其中, T是电机的输出力矩, Te为额定扭矩, Pe为额定功率, n为转速, ne为额定转速。
经过传动系电机传递到车轮处的力矩为
| $ {\mathit{\boldsymbol{T}}_{dij}} = {\mathit{\boldsymbol{T}}_{ij}} \cdot i \cdot {\eta _T}。$ | (18) |
其中, Tdij为后轮处的驱动力矩, Tij为电机输出力矩, i为传动比,取i=3, ηT为传动系的机械效率,ηT=0.9[13]。
2 车辆操纵稳定性的控制目标当质心侧偏角较小时, 通过横摆角速度的变化情况, 可以较好地反映出车辆的稳定性情况。但是在极限工况下, 质心侧偏角较大, 此时即使横摆角速度很小, 车辆也会出现急转和侧滑等失稳现象, 因此,仅将横摆角速度作为单一变量对操纵稳定性进行控制, 在极限工况下不能很好地保证车辆的行驶轨迹和理想轨迹一致以及车辆的稳定性, 同样, 如果仅选取质心侧偏角作为单一变量, 则不能很好响应期望横摆角速度, 也不能使车辆运行过程中的稳定性保持较好。
因此, 本文将横摆角速度和质心侧偏角结合起来作为控制变量。根据直接横摆力矩的控制目标, 即基于线性二自由度车辆模型得到的理想横摆角速度ωd和理想质心侧偏角βd[14-15]。
横摆角速度和质心侧偏角的传递函数为
| $ \frac{{{\omega _{\rm{r}}}}}{\delta }\left( s \right) = {G_r} \cdot \frac{{{\tau _1}s + 1}}{{{\mathit{\boldsymbol{T}}_2}{s^2} + {\mathit{\boldsymbol{T}}_1}s + 1}}, $ | (19) |
| $ \frac{\beta }{\delta }\left( s \right) = {G_\beta } \cdot \frac{{{{\tau '}_1}s + 1}}{{{\mathit{\boldsymbol{T}}_2}{s^2} + {\mathit{\boldsymbol{T}}_1}s + 1}}。$ | (20) |
其中, Gr为横摆角速度稳态增益, Gβ为质心侧偏角稳态增益。
| $ {G_{\rm{r}}} = \frac{u}{{L \cdot \left( {1 + K{u^2}} \right)}}, $ | (21) |
| $ {G_\beta }{\rm{ = }}\frac{{b - ma{u^2}/\left( {{k_2} \cdot L} \right)}}{{L \cdot \left( {1 + K{u^2}} \right)}}。$ | (22) |
其中,
由式(21)可得, 横摆角速度的理想值为
| $ {\omega _{\rm{d}}} = {G_{\rm{r}}} \cdot \delta = \frac{{u \cdot \delta }}{{L \cdot \left( {1 + K{u^2}} \right)}}。$ | (23) |
由于车辆在行驶时受到路面附着条件的限制, 其侧向加速度应受到如下约束,
| $ \left| {{a_y}} \right| \le \mu \cdot g。$ | (24) |
其中, ay为侧加速度, 当车辆的质心侧偏角很小时有
| $ {a_y} \approx u \cdot {\omega _{\rm{r}}}。$ | (25) |
联立式(24)和(25)可得,理想横摆角速度还应满足
| $ {\omega _{\rm{r}}} \le \left| {\frac{{\mu \cdot g}}{u}} \right|。$ | (26) |
综上可得, 理想横摆角速度ωd应为以上两个值绝对值的最小值[16], 即
| $ {\omega _{\rm{d}}} = \min \left| {\frac{{u \cdot \delta }}{{L \cdot \left( {1 + K{u^2}} \right)}}} \right|,\left| {\frac{{\mu \cdot g}}{u}} \right|。$ | (27) |
由式(22)可得,质心侧偏角的理想值为
| $ {\beta _{\rm{d}}} = {G_\beta } \cdot \delta = \frac{{b - ma{u^2}/\left( {{k_2} \cdot L} \right)}}{{L \cdot \left( {1 + K{u^2}} \right)}} \cdot \delta 。$ | (28) |
同样地, 质心侧偏角的最大值也受到路面附着条件的限制。由式(28)可得
| $ {\beta _{\rm{d}}} = {\omega _{\rm{r}}}u \cdot \frac{b}{{{u^2}}} - \frac{{ma}}{{{k_2}L}}。$ | (29) |
从而得到理想质心侧偏角的最大值为
| $ {\beta _{\rm{d}}} = \mu g\frac{b}{{{u^2}}} - \frac{{ma}}{{{k_2}L}}。$ | (30) |
另外, 当轮胎与路面间的侧向附着力达到极限时, 在干沥青路面上质心侧偏角的特征值为βT=±10°, 在冰雪路面上其特征值为βT=±2°[17]。
综上可得,为了适应不同的路面附着条件, 理想质心侧偏角βd应为以上3个值的绝对值的最小值, 即
| $ \begin{array}{l} {\beta _{\rm{d}}} = \min \left| {\frac{{b - ma{u^2}/\left( {{k_2} \cdot L} \right)}}{{L \cdot \left( {1 + K{u^2}} \right)}} \cdot \delta } \right|,\\ \left| {\mu g\frac{b}{{{u^2}}} - \frac{{ma}}{{{k_2}L}}} \right|,\left| {{\beta _T}} \right|。\end{array} $ | (31) |
横摆角速度和质心侧偏角是评价车辆稳定性控制策略效果的关键参数[18], 横摆角速度可以通过惯性导航或陀螺仪等传感器直接测量, 而质心侧偏角很难通过传感器直接测量, 因此需要通过其他参数估计获得[19]。
车辆质心侧偏角和前后轮轮胎的侧向力有关, 而车辆在非稳定区常表现出强烈的非线性特征, 因此选用扩展卡尔曼滤波的方法对其进行估算[20]。
基于线形二自由度车辆模型, 整车的侧向和横摆运动微分方程经过变换后得到
| $ \left\{ \begin{array}{l} \dot \beta = \frac{{{F_{Y1}}\cos \left( {\delta - \beta } \right) + {F_{Y2}}\cos \beta }}{{mu}} - {\omega _{\rm{r}}},\\ {{\dot \omega }_{\rm{r}}} = \frac{{a{F_{Y1}}\cos \delta - b{F_{Y2}}}}{{{I_z}}} \end{array} \right. $ | (32) |
运用扩展卡尔曼滤波进行质心侧偏角估计时, 忽略轮胎侧倾角影响后, 对轮胎的侧向力进行描述[21],
| $ \begin{array}{l} {{\bar F}_Y}\left( \alpha \right) = D\sin \left[ {C \cdot a\tan \left( {B\alpha - BE\alpha + E \cdot } \right.} \right.\\ \left. {\left. {a\tan \left( {B\alpha } \right)} \right)} \right]。\end{array} $ | (33) |
其中, D,C,B,E均是与路面附着系数和轮胎载荷有关的轮胎侧向力参数。
为了更好地描述轮胎的侧向力瞬态特性, 用轮胎的松弛长度ly来表征轮胎力随车辆运行状态的瞬时变化特性, 即
| $ {{\dot F}_Y} = \frac{u}{{{l_y}}}\left( {{{\bar F}_Y}\left( \alpha \right) - {F_Y}} \right)。$ | (34) |
结合式(32)可以得到非线性的车辆二自由度模型
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot X}} = f\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{U}}} \right) + \mathit{\boldsymbol{W}},\\ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{HX}} + \mathit{\boldsymbol{V}}。\end{array} \right. $ | (35) |
其中, X=[β ωr FY1 FY2]T, Y=[ay ωr]T, U=[δ]。
| $ \begin{array}{l} f\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{U}}} \right) = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{{F_{Y1}}\cos \left( {\delta - \beta } \right) + {F_{Y2}}\cos \beta }}{{mu}} - {\omega _{\rm{r}}}}\\ {\frac{{a{F_{Y1}}\cos \delta - b{F_{Y2}}}}{{{I_z}}}}\\ {\frac{{{v_x}}}{{{l_y}}}\left( {{{\mathit{\boldsymbol{\bar F}}}_{Y1}}\left( {\beta ,{\omega _r},\delta } \right) - {F_{Y1}}} \right)}\\ {\frac{{{v_x}}}{{{l_y}}}\left( {{{\mathit{\boldsymbol{\bar F}}}_{Y2}}\left( {\beta ,{\omega _r},\delta } \right) - {F_{Y2}}} \right)} \end{array}} \right], \end{array} $ | (36) |
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 0&0&{\frac{1}{m}}&{\frac{1}{m}}\\ 0&1&0&0 \end{array}} \right]。$ | (37) |
对于式(35)描述的非线性系统, 将其离散化可以得到
| $ x\left( {k + 1} \right) = x\left( k \right) + f\left( {x\left( k \right),u\left( k \right)} \right) \cdot T。$ | (38) |
其中,T为计算步长。
给定该系统的初始状态为
| $ x\left( 0 \right) = {\left[ {0\;0\;0\;0} \right]^{\rm{T}}}。$ | (39) |
上文已经获得了理想横摆角速度和理想质心侧偏角, 并通过扩展卡尔曼滤波的方法估计获得质心侧偏角, 这些参数将作为附加横摆力矩控制器的输入量。为了验证控制效果, 本文设计了基于PID控制、基于模糊逻辑控制以及基于PID模糊逻辑联合控制的附加横摆力矩控制器。
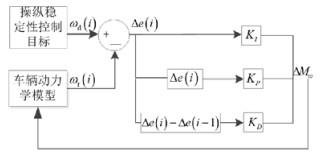
4.1 基于PID控制的附加横摆力矩控制器基于PID控制的附加横摆力矩控制结构图如图 3所示[22], 其中理想横摆角速度与横摆角速度的偏差值作为PID控制器的输入变量, 以附加横摆力矩作为输出量。
|
图 3 基于PID的控制系统结构图 Fig. 3 Control system based on PID |
| $ 令\;\;\;e\left( i \right) = {\omega _{\rm{d}}}\left( i \right) - {\omega _{\rm{r}}}\left( i \right), $ | (40) |
| $ 则\;\;\;\Delta e\left( i \right) = e\left( i \right) - e\left( {i - 1} \right), $ | (41) |
| $ \begin{array}{l} {M_\omega }\left( i \right) = {K_P}e\left( i \right) + {K_l}\sum\limits_{j = 0}^i {e\left( j \right)} + \\ {K_D}\left( {e\left( i \right) - e\left( {i - 1} \right)} \right), \end{array} $ | (42) |
| $ \begin{array}{l} {M_\omega }\left( {i - 1} \right) = {K_P}e\left( {i - 1} \right) + {K_I}\sum\limits_{j = 0}^{i - 1} {e\left( j \right)} + \\ {K_D}\left( {e\left( {i - 1} \right) - e\left( {i - 2} \right)} \right)。\end{array} $ | (43) |
由式(41)和式(42)可得基于PID控制的附加横摆力矩ΔMω,
| $ \begin{array}{l} \Delta {M_\omega } = {K_P}\Delta e\left( i \right) + {K_I}e\left( i \right) + {K_D}\left( {\Delta e\left( i \right) - } \right.\\ \left. {\Delta e\left( {i - 1} \right)} \right)。\end{array} $ | (44) |
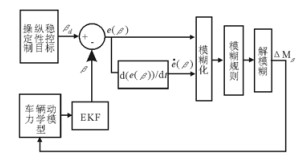
基于模糊逻辑控制的附加横摆力矩控制结构图如图 4所示。
|
图 4 基于模糊逻辑的控制系统结构图 Fig. 4 Control system based on fuzzy logic control |
图 4中, 控制器以车辆质心侧偏角的理想值βd与其估计值β的偏差e(β),以及偏差的变化率
在具体的模糊逻辑控制过程中, 规范化后的偏差E、偏差变化率EC以及控制量U的模糊集和论域定义如下:
E的模糊集为{NB, NM, NS, ZE, PS, PM, PB};
E的论域为[-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1];
EC的模糊集为{NB, NM, NS, ZE, PS, PM, PB};
EC的论域为[-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1];
U的模糊集为{ZE, PS, PM, PB};
U的论域为[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1]。
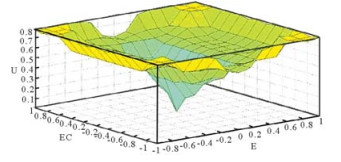
上述E和EC各有7个模糊语言变量, 因此模糊控制器的模糊规则共49条, 图 5为建立的模糊规则曲面。
|
图 5 模糊逻辑控制的模糊规则曲面 Fig. 5 Fuzzy logic control regular surface |
将基于PID控制得出的附加横摆力矩ΔMω和基于模糊逻辑控制得出的附加横摆力矩ΔMβ经合适的加权因子Aω和Aβ加权, 从而输出基于PID模糊逻辑联合控制的附加横摆力矩值ΔM, 对车辆的操纵稳定性进行更好的调节, 即
| $ \Delta M = {A_\omega } \cdot \Delta {M_\omega } + {A_\beta } \cdot \Delta {M_\beta }。$ | (43) |
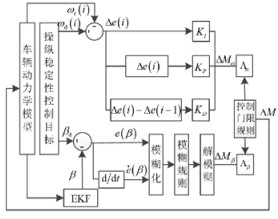
本文设计的基于PID模糊逻辑联合控制的附加横摆力矩控制器的结构图如图 6所示。
|
图 6 基于PID模糊逻辑联合控制的系统结构图 Fig. 6 Control system based on PID-fuzzy logic control |
以FSAE纯电动赛车为平台, 根据其行驶工况, 结合Matlab/Simulink中设计的仿真模型, 选择方向盘转角阶跃输入工况和双移线工况[24]进行仿真分析, 对提出的操纵稳定性控制策略进行仿真验证。整车基本参数如表 2所示。
|
|
表 2 整车基本参数 Tab. 2 Vehicle basic parameters |
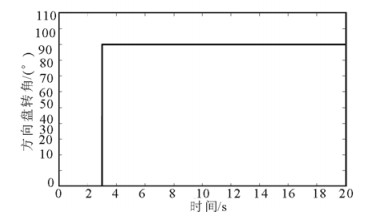
方向盘转角随时间的阶跃输入如图 7所示, 仿真时间为20s, 路面附着系数为0.4。分别在50km/h,70km/h,90km/h这3个初始车速下, 对比验证PID控制、PID模糊逻辑联合控制两种控制策略对提高车辆操纵稳定性的有效性。
|
图 7 方向盘转角阶跃输入 Fig. 7 Steering wheel angular step input |
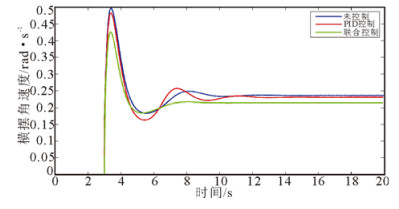
1) 初始车速为50km/h时, 不加控制、PID控制以及联合控制3种情况下, 车辆横摆角速度和质心侧偏角的仿真结果如图 8和9所示。
|
图 8 初速度50km/h时横摆角速度对比曲线 Fig. 8 Yaw rate at the initial speed of 50km/h |
|
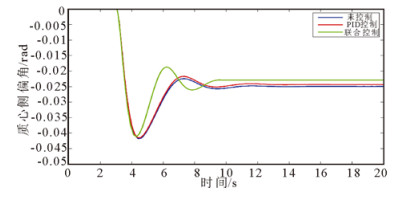
图 9 初速度50km/h时质心侧偏角对比曲线 Fig. 9 Sideslip angle at the initial speed of 50km/h |
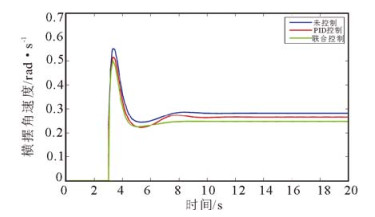
2) 初始车速为70km/h时, 不加控制、PID控制以及联合控制3种情况下, 车辆横摆角速度和质心侧偏角的仿真结果如图 10和11所示。
|
图 10 初速度70km/h时横摆角速度对比曲线 Fig. 10 Yaw rate at the initial speed of 70km/h |
|
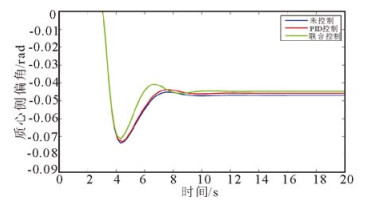
图 11 初速度70km/h时质心侧偏角对比曲线 Fig. 11 Sideslip angle at the initial speed of 70km/h |
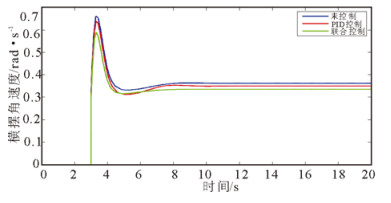
3) 初始车速为90km/h时, 不加控制、PID控制以及联合控制3种情况下, 车辆横摆角速度和质心侧偏角的仿真结果如图 12和13所示。
|
图 12 初速度90km/h时横摆角速度对比曲线 Fig. 12 Yaw rate at the initial speed of 90km/h |
|
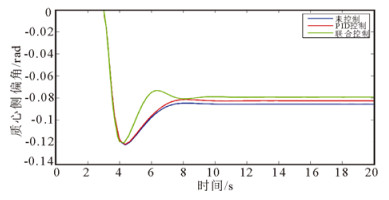
图 13 初速度90km/h时质心侧偏角对比曲线 Fig. 13 Sideslip angle at the initial speed of 90km/h |
车辆横摆角速度和质心侧偏角的响应指标变化归纳如表 3所示。通过对比在此工况的不同初始车速下, 无控制、PID控制和基于PID模糊逻辑联合控制下的横摆角速度和质心侧偏角仿真结果及其响应指标变化可得:
|
|
表 3 各控制策略方向盘角阶跃输入下响应指标 Tab. 3 The feature of the yaw rate and sideslip angle with three control strategy |
1) 在方向盘转角阶跃输入情况下, 由仿真结果可以看出,横摆角速度和质心侧偏角都是收敛的, 而且随着初始车速的增加, 稳态值都是增加的。
2) 不同初始车速下, 联合控制时车辆的横摆角速度的稳态值相对于无控制和PID控制分别减少了9.15%和7.11%(初速度50km/h),12.17%和6.62%(初速度70km/h),7.51%和4.18%(初速度90km/h), 提高了车辆的稳定性。不加控制、PID控制以及联合控制时, 横摆角速度的收敛速度依次加快, 并且联合控制时的收敛速度明显快于另外两种情况。
3) 不同初始车速下, 联合控制时车辆的质心侧偏角的稳态值相对于无控制和PID控制分别减少了8.4%和5.76%(初速度50km/h),4.88%和2.18%(初速度70km/h),7.48%和4.12%(初速度90km/h), 提高了车辆的稳定性。同样地, 不加控制、PID控制以及联合控制时, 质心侧偏角的收敛速度依次加快, 并且联合控制时的收敛速度明显快于另外两种情况。
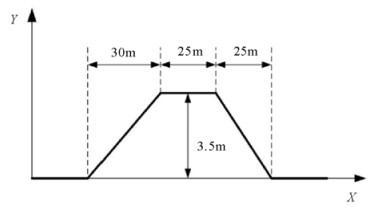
5.1.2 双移线工况仿真双移线工况是测试车辆操纵稳性的典型行驶工况, 在该工况下, 当车速较高时, 由于沿规定路径行驶时转向盘转角的迅速变化, 车辆的后轴就不能立即建立侧向力, 车辆可能发生侧滑甚至发生激转。车辆在这种较短时间的极限工况下运行, 就可以测试所用操纵稳定性控制策略能否满足要求, 分析仿真结果也可以对控制策略做出评价[25]。在仿真验证中, 双移线工况的路径示意图如图 14所示。
|
图 14 双移线工况的路径示意图 Fig. 14 The path of the double lane change |
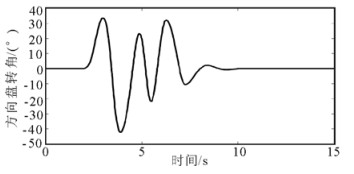
双移线工况中, 车辆的初始速度为70km/h, 路面附着系数为0.4, 仿真时间为15s, 方向盘转角输入如图 15所示[26]。
|
图 15 双移线工况下的方向盘转角输入 Fig. 15 Steering wheel Angle input in double lane change |
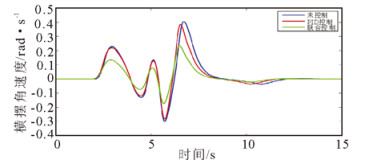
在此工况下, 不加控制、PID控制以及联合控制时, 车辆横摆角速度和质心侧偏角的仿真结果如图 16和图 17所示。
|
图 16 双移线工况下横摆角速度对比曲线 Fig. 16 Yaw rate at double lane change |
|
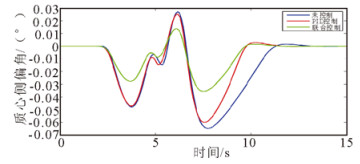
图 17 双移线工况下质心侧偏角对比曲线 Fig. 17 Sideslip angle at double lane change |
由以上仿真结果可得, 车辆横摆角速度和质心侧偏角的响应指标变化如表 4所示。通过对比不加控制、PID控制以及联合控制3种情况下, 横摆角速度和质心侧偏角仿真控制结果及其响应指标变化可得:
|
|
表 4 横摆角速度和质心侧偏角的响应指标变化 Tab. 4 The feature of the yaw rate and sideslip angle |
1) 在双移线工况下, 联合控制时,车辆的横摆角速度的峰值相对于无控制和PID控制时的相应峰值最多分别减少了43.87%和38.91%, 由此说明采用联合控制方法能够有效提高车辆的稳定性; 采用不加控制、PID控制以及联合控制时, 横摆角速度的收敛速度依次加快, 并且联合控制时的收敛速度明显快于另外两种情况。
2) 在双移线工况下, 联合控制时车辆的质心侧偏角的峰值相对于无控制和PID控制时的相应峰值最多分别减少了49.08%和68.53%, 提高了车辆的稳定性; 同样地, 不加控制、PID控制以及联合控制时, 质心侧偏角的收敛速度依次加快, 并且联合控制时收敛速度明显快于另外两种情况。
通过以上方向盘转角阶跃输入和双移线两种工况下仿真结果分析可知, 所提出的PID模糊逻辑联合控制策略相比PID控制策略能够更好地、快速地实现车辆的稳定性控制。
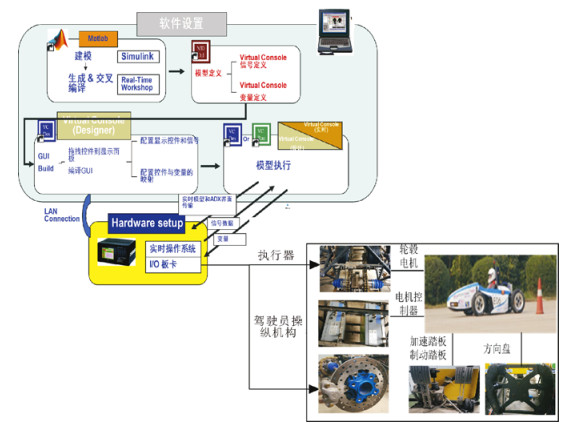
5.2 试验研究与结果分析 5.2.1 FSAE纯电动赛车硬件在环试验平台搭建为了验证本文提出的FSAE纯电动赛车稳定性控制策略的有效性和可行性, 针对电动汽车控制策略开发周期长、成本高等问题, 本文利用A & D5435半实物仿真平台和Matlab/Simulink的代码自动生成技术, 搭建了如图 18所示的FSAE纯电动赛车硬件在环试验平台。利用Matlab/Simulink的RTW技术, 将前文搭建的PID模糊逻辑联合控制策略模型编译下载到A & D5435中, 其中, A & D5435分别采集方向盘转角、加速踏板开度、制动踏板开度等驾驶员操纵信息, 车辆纵向车速、侧向车速、横摆角速度、纵向加速度、侧向加速度等车辆行驶状态信息, A & D5435输出为驱动电机扭矩信号, 同时, A & D5435还能对实车试验中信号进行动态显示、记录及保存。
|
图 18 FSAE纯电动赛车硬件在环平台试验平台 Fig. 18 FSAE pure electric car hardware test platform |
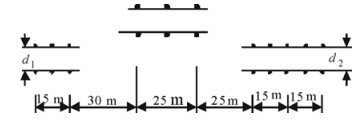
利用本文建立的双电机驱动电动汽车半实物仿真试验平台, 选取典型工况-双移线工况进行了PID模糊逻辑联合控制策略试验研究。ISO3888-1双移线试验工况可以模拟车辆在道路上超车的操作, 试验场地的路面附着系数为0.6,试验工况如图 19所示。其中,d1=1.1L+0.25, d2=1.3L+0.25, L为车宽。
|
图 19 双移线试验路线示意图 Fig. 19 Test path of double lane change |
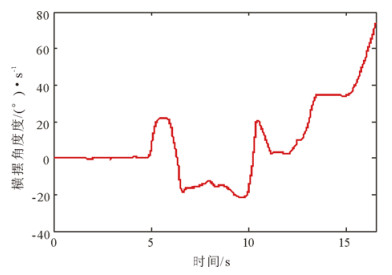
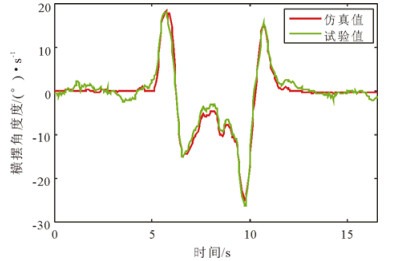
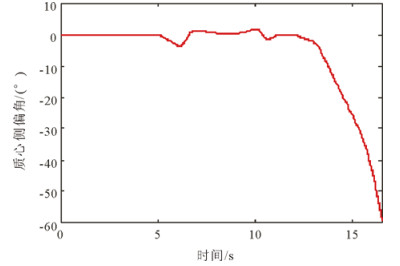
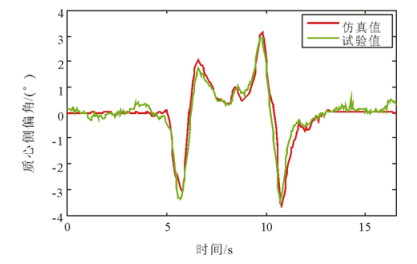
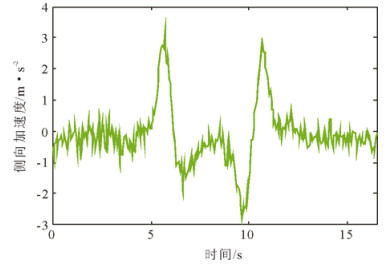
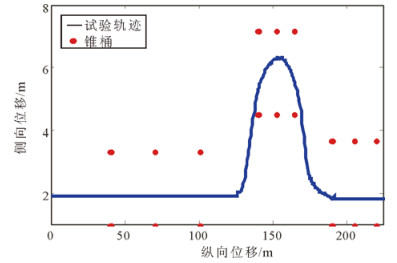
在此工况下, 有稳定性控制和无稳定性控制车辆横摆角速度、质心侧偏角、侧向加速度及行驶轨迹分别如图 20~25所示。图 20和图 22为无稳定性控制状态, 12.86s时车辆的横摆角速度和质心侧偏角急剧增大, 无稳定性控制横摆角速度的峰值为77.9744°/s, 无稳定性控制质心侧偏角的峰值为-59.5082°, 在此状态下车辆失去了行驶稳定性。图 21和图 23为在稳定性控制系统作用下的车辆横摆角速度和质心侧偏角曲线, 此时, 车辆的质心侧偏角和横摆角速度被控制在合理的范围内, 车辆的侧向加速度被限制在0.4g以内。如图 24和图 25分别为试验获得的车辆在稳定性控制策略工作状态下的侧向加速度和行驶轨迹, 可以看出,车辆在稳定性系统的作用下行驶稳定, 未发生侧滑、甩尾等危险状态, 有效改善了车辆的行驶稳定性。
|
图 20 无稳定性控制横摆角速度曲线 Fig. 20 Yaw rate of double lane change without control |
|
图 21 有稳定性控制横摆角速度曲线 Fig. 21 Yaw rate of double lane change with control |
|
图 22 无稳定性控制质心侧偏角曲线 Fig. 22 Sideslip angle of double lane change without control |
|
图 23 有稳定性控制质心侧偏角曲线 Fig. 23 Sideslip angle of double lane change with control |
|
图 24 有稳定性控制侧向加速度曲线 Fig. 24 Lateral acceleration of double lane change with control |
|
图 25 有稳定性控制车辆行驶轨迹 Fig. 25 Trace of double lane change with control |
仿真和试验得到的横摆角速度平均误差为6.94%, 最大误差为9.705%。仿真获得的质心侧偏角和试验获得的质心侧偏角平均误差为5.058 3%, 最大误差为7.416%。表明仿真模型精度较高, 可以满足车辆稳定性控制系统工作需求。
因此, 仿真和试验结果表明, 本文提出的PID模糊逻辑联合控制策略可以在双电机驱动纯电动赛车出现失稳状态时,有效提高车辆的操纵稳定性。
6 结语1) 本文以FSAE纯电动赛车为平台, 以质心侧偏角和横摆角速度为控制目标, 设计了基于PID模糊逻辑联合控制的车辆操纵稳定性控制策略, 并结合Matlab/Simulink中设计的仿真模型, 选择方向盘转角阶跃输入工况和双移线工况, 对提出的PID模糊逻辑联合控制操纵稳定性控制策略进行仿真验证。利用A & D5435半实物仿真平台和Matlab/Simulink的代码自动生成技术, 搭建了FSAE纯电动赛车硬件在环试验平台, 并进行了双移线工况的实车试验验证。结果表明:在方向盘转角阶跃输入工况和双移线工况下, 在不加控制、PID控制以及联合控制3种情况下, 联合控制均能使车辆的横摆角速度和质心侧偏角保持较小。不加控制、PID控制以及联合控制时横摆角速度和质心侧偏角的收敛速度也依次加快, 联合控制时的收敛速度明显快于另外两种情况。说明所提出的PID模糊逻辑联合控制策略能够改善车辆的侧向动态响应特性, 提高了车辆的操纵稳定性。
2) 本文在以下方面还需要进行进一步的研究:①车辆是一个比较复杂的非线性系统, 但是本文在研究过程中根据需要对模型进行了简化, 没有考虑悬架系统以及电池动态特性等影响, 因此,在以后的建模中需要进行改进, 提高建模精度;②由于控制器的开发周期长、成本高等问题,文中采用半实物仿真技术对控制策略进行了试验验证, 但是控制系统的良好运行不仅需要先进的控制策略还需要可靠的硬件系统,因此,控制器硬件系统开发也是之后研究的重点内容。
| [1] |
张浩.客车操纵稳定性分析及其控制策略研究[D].长春: 吉林大学, 2012.
|
| [2] |
褚端峰.客车行驶稳定性控制的关键技术研究[D].武汉: 武汉理工大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10497-1011058068.htm
|
| [3] |
余志生. 汽车理论[M]. 北京: 机械工业出版社, 2012.
|
| [4] |
REEDY J, LUNZMAN S, MEKARI B. Model based design accelerates the development of mechanical locomotive controls[J]. Intelligent Vehicles Symposium IEEE, 2010, 32(14): 1098-1103. |
| [5] |
NAGAI M, SHINO M, GAO F. Study on integrated control of active front steer angle and direct yaw moment[J]. Jsae Review, 2002, 23(3): 309-315. DOI:10.1016/S0389-4304(02)00189-3 |
| [6] |
LU J, MESSIH D, SALIB A, et al. An enhancement to an electronic stability control system to include a rollover control function[J]. Sae Transactions, 2007, 116: 303-313. |
| [7] |
SILL J H, AYALEW B. Saturation balancing control for enhancing dynamic stability of vehicles with independent wheel drives[C]//SAE 2011 World Congress Exhibition.SAE, 2011.
|
| [8] |
王金湘, 陈南, 皮大伟. 基于横摆角速度变门限值的车辆稳定性控制策略及实车场地试验[J]. 汽车工程, 2008, 30(3): 222-226. DOI:10.3321/j.issn:1000-680X.2008.03.008 |
| [9] |
陈无畏, 祝辉. 基于状态识别的整车操纵性和平顺性的协调控制[J]. 机械工程学报, 2011, 47(6): 121-129. |
| [10] |
TAHAMI F, FARHANGI S, KAZEMI R. A fuzzy logic direct yaw-moment control system for all-wheel-drive electric vehicles[J]. Vehicle System Dynamics, 2004, 41(3): 203-221. DOI:10.1076/vesd.41.3.203.26510 |
| [11] |
王其东, 黄鹤, 陈无畏, 等. 基于自适应FFRLS的汽车前后轴侧偏刚度估计[J]. 机械工程学报, 2012, 48(12): 110-117. |
| [12] |
玄圣夷, 宋传学, 靳立强, 等. 基于多级鲁棒PID控制的汽车稳定性控制策略[J]. 吉林大学学报(工学版), 2010, 40(1): 13-18. |
| [13] |
张金柱, 张洪田, 孙远涛. 电动汽车稳定性的横摆力矩控制[J]. 电机与控制学报, 2012, 16(6): 75-80. DOI:10.3969/j.issn.1007-449X.2012.06.013 |
| [14] |
肖闯.汽车稳定性控制方法仿真研究[D].长沙: 湖南大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10532-2007160909.htm
|
| [15] |
吕红明, 陈南, 王琪. Matlab环境下车辆的开环操纵稳定性仿真[J]. 盐城工学院学报(自然科学版), 2004, 17(1): 21-24. DOI:10.3969/j.issn.1671-5322.2004.01.006 |
| [16] |
ZANTEN A T V. VDC, the vehicle dynamics control system of Bosch[J]. Advancements in Abs/tcs & Brake Technology Sae, 1995. |
| [17] |
刘旭程.基于差动制动的汽车横向稳定性控制研究及仿真分析[D].南宁: 广西大学, 2015. http://www.cnki.com.cn/Article/CJFDTotal-GXJX201507014.htm
|
| [18] |
郭孔辉, 付皓, 丁海涛. 基于扩展卡尔曼滤波的汽车质心侧偏角估计[J]. 汽车技术, 2009(4): 1-3+44. DOI:10.3969/j.issn.1000-3703.2009.04.001 |
| [19] |
SASAKI H, NISHIMAKI T. A side slip angle estimation using neural network for a wheeled vehicle[J]. SAE Technical Paper, 2000. |
| [20] |
郭张军, 徐建光, 刘佳佳. 基于Kalman滤波融合算法的某坝基水平位移综合信息提取[J]. 盐城工学院学报(自然科学版), 2010, 23(2): 30-34. |
| [21] |
BAKKER E. A new tire model with an application in vehicle dynamics studies[J]. SAE Technical Paper, 1989, 98. |
| [22] |
周红妮.车辆稳定性控制方法于策略的比较研究[D].武汉: 武汉科技大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11915-2007090017.htm
|
| [23] |
刘曙光, 魏俊民, 竺志超. 模糊控制技术阅[M]. 北京: 中国纺织出版社, 2002.
|
| [24] |
郭应时, 袁伟. 汽车试验学[M]. 北京: 人民交通出版社, 2006.
|
| [25] |
YI K, CHUNG T, KIM J, et al. An investigation into differential braking strategies for vehicle stability control[J]. Journal of Automobile Engineering, 2003, 217(12): 1081-1094. DOI:10.1243/09544070360729428 |
| [26] |
黄程程.基于自适应卡尔曼滤波的汽车质心侧偏角估算研究[D].长春: 吉林大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011100203.htm
|
 2018, Vol. 48
2018, Vol. 48