2. 国网辽宁省电力有限公司,辽宁 沈阳 110004;
3. 上海电缆研究所, 上海 200093
2. State Grid Liaoning Electric Power Co., Ltd., Shenyang 110004, China;
3. Shanghai Electric Cable Research Institute, Shanghai 200093, China
随着用户对用电量和电能质量的需求越来越高, 2009年, 国家电网公司开始全面推进智能电网建设。智能电网综合运用了先进的传感、测量、通信和控制技术, 从而使电网可以安全、可靠、经济有效地运行。然而, 智能电网的快速发展使用户与电网之间的实时信息呈现爆发式增长, 对电力通信提出了更高的要求[1]。光纤抗电磁干扰能力强、工作性能可靠且通信容量大、重量轻、成本低, 是电力系统通信的重要组成部分。
光纤复合低压电缆(OPLC)创新性地将光纤和电力电缆绞合在一起, 从而有效避免了网络建设时二次布线施工, 降低了网络建设和重复施工等费用。光纤复合低压电缆可同时接入宽带和用电设备:利用无源光网络技术, 可实现视频、语音及数据的远程传输; 通过IOT技术可实现远程抄表、电表数据的透明传输, 通知及缴费等[2]。
但是, 交流电缆工作时, 在铜损、介电损耗和电缆短路产生大电流的综合作用下, 电缆升温成为热源。通过热传递, 光单元的温度升高, 产生热膨胀, 影响光纤结构, 甚至导致严重的热变形, 从而会影响光纤的传输特性。针对OPLC的温度分布及传输特性, 前人已做过相关研究[3], 但本文是将OPLC的温度、应力、传输特性联合起来进行多物理场仿真。本文采用多物理场仿真软件COMSOL。首先,分别求解OPLC正常工作与短路后温度场与应力场耦合作用下光纤的热变形,然后,在两种状态引起的热变形的基础上研究光纤的传输特性, 对比分析短路故障对光纤传输特性的影响。
1 温度应力耦合模型物体在一定温度条件下工作时, 热胀冷缩现象会使得物体形状随着温度的变化而变化。但是, 若物体各部分没有任何约束, 可自由发生形变, 则虽有形变却并不会产生应力; 反之, 若物体表面固定或与其他物体相连使得形变不能自由发生,则会出现附加应力, 这就是所谓的热应力。忽略变温对材料性能的影响, 为了求得热应力, 首先应该求得物体的温度场, 然后按弹性力学的基本方程求解物体的热应力。
1.1 温度分布计算模型架空敷设OPLC的温度分布问题, 可以看成是有内热源的稳态二维热传导问题。根据热力学第一定律和傅里叶定律, 用于计算电力电缆温度场的控制方程[4-5]为
| $ \rho {C_\rho }\frac{{\partial T}}{{\partial t}} + \rho {C_\rho }u \cdot \nabla T = \nabla \cdot \left( {K\nabla T} \right) + Q。$ | (1) |
其中:ρ为密度, 单位为kg/m3; T为电缆某一时刻的温度, 单位为K; Cρ为比热容, 单位为J/(kg·K); k为导热系数, 单位为W/(m·K); ρCρ·∂T/∂t为电缆内总的热积聚; ρCρu·▽T为对流散失的热量, 其中u是动力黏度, 假设电缆内部填充为实, 此项应该为0;▽·(k▽T)为热传导项; Q为电缆通电时导体产生的热量, 即每单位体积的加热功率。
为了具体确定OPLC的温度分布情况, 还需要知道初始条件和边界条件[6-8]。
初始条件, 即OPLC初始状态中每个点的温度是已知的,如式(2)所示,
| $ T\left| {_{t = 0}} \right. = f\left( {x,y} \right)。$ | (2) |
其中, f(x, y)为OPLC每个点初始状态下的温度分布。
第一类边界条件, 即稳定状态时边界每个点的温度已知, 如式(3)所示,
| $ T\left| {_{t = \infty }} \right. = f\left( {x,y} \right)。$ | (3) |
其中, f(x, y)表示OPLC每个点稳定状态下的温度分布。
第二类边界条件即已知左右边界面上的法向热流密度值, 可表示为式(4),
| $ \frac{{\partial T}}{{\partial n}}\left| {_{{\mathit{\Gamma }_i}}} \right. = 0。$ | (4) |
其中, Γi为OPLC左右边界。
第三类边界条件指OPLC在与空气接触边界上与流体按式(5)中的牛顿定律进行自然的热交换,
| $ - k\frac{{\partial T}}{{\partial n}}\left| {_\mathit{\Gamma }} \right. = h\left( {T - {T^f}} \right)。$ | (5) |
其中, Γ为与空气接触的轴边界, Tf为空气温度, h为热对流系数, k为导热系数。
1.2 应力计算模型本文以光纤为研究对象, 建立如下基本计算方程。
连续介质内部任意区域的平衡方程[9]为
| $ \left\{ \begin{array}{l} \frac{{\partial {\sigma _x}}}{{\partial x}} + \frac{{\partial {\tau _{xy}}}}{{\partial y}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}} + X = 0,\\ \frac{{\partial {\tau _{yx}}}}{{\partial x}} + \frac{{\partial {\sigma _y}}}{{\partial y}} + \frac{{\partial {\tau _{yz}}}}{{\partial z}} + Y = 0,\\ \frac{{\partial {\tau _{zx}}}}{{\partial x}} + \frac{{\partial {\sigma _{zy}}}}{{\partial y}} + \frac{{\partial {\tau _z}}}{{\partial z}} + Z = 0。\end{array} \right. $ | (6) |
其中, σx, σy, σz为笛卡尔坐标下的正应力分量; τxy, τxz, τyx, τyz, τzx, τzy为切应力; X, Y, Z为物体受到的各向载荷力分量。
根据胡克定律[10], 应力和应变之间的关系式为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\varepsilon }}_x} = \frac{1}{\xi }\left[ {{\mathit{\boldsymbol{\sigma }}_x} - \mu \left( {{\mathit{\boldsymbol{\sigma }}_y} + {\mathit{\boldsymbol{\sigma }}_z}} \right)} \right] + \alpha T,{\gamma _{xy}} = \frac{1}{G}{\tau _{xy}},\\ {\mathit{\boldsymbol{\varepsilon }}_y} = \frac{1}{\xi }\left[ {{\mathit{\boldsymbol{\sigma }}_y} - \mu \left( {{\mathit{\boldsymbol{\sigma }}_z} + {\mathit{\boldsymbol{\sigma }}_x}} \right)} \right] + \alpha T,{\gamma _{yz}} = \frac{1}{G}{\tau _{yz}},\\ {\mathit{\boldsymbol{\varepsilon }}_z} = \frac{1}{\xi }\left[ {{\mathit{\boldsymbol{\sigma }}_z} - \mu \left( {{\mathit{\boldsymbol{\sigma }}_x} + {\mathit{\boldsymbol{\sigma }}_y}} \right)} \right] + \alpha T,{\gamma _{zx}} = \frac{1}{G}{\tau _{zx}}。\end{array} \right. $ | (7) |
其中, σ为应力张量, ξ为材料弹性模量, μ是泊松比, G为剪切弹性模量, ε为应变张量。
弹性力学的几何方程[11]为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\varepsilon }}_x} = \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial x}},{\gamma _{xy}} = \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial x}},\\ {\mathit{\boldsymbol{\varepsilon }}_y} = \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial y}},{\gamma _{yz}} = \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial z}} + \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial y}},\\ {\mathit{\boldsymbol{\varepsilon }}_z} = \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial z}},{\gamma _{zx}} = \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial z}}。\end{array} \right. $ | (8) |
其中, εx, εy, εz为直角坐标下各向的应变张量; u, v, w为直角坐标下各向的位移分量; γxy, γyz, γzx为坐标间的剪应变。
式(6)~(8)构成了OPLC的应力计算数学模型。
1.3 温度场耦合应力场的计算方法热胀冷缩也是光纤材料二氧化硅的基本属性之一, 所以OPLC温度的变化会使光纤发生膨胀, 从而影响光纤的热应变张量。假设物体由参考状态时的温度Tref(应变为0时的温度)升高至T时, 物体内部将发生膨胀, 设膨胀为正, 则由温度变化引起的应变为[12]
| $ {\mathit{\boldsymbol{\varepsilon }}_{{\rm{th}}}} = \alpha \left( {T - {T_{{\rm{ref}}}}} \right)。$ | (9) |
其中, εth为热应变张量, α为热膨胀系数, T为物体温度, Tref为参考温度。式(9)给出了温度场耦合应力场的计算方法。
1.4 OPLC光单元热变形仿真分析本文以铜芯PVC绝缘OPLC为例, 研究当铜导体温度达到某一值时,光纤的应力特性和传输特性。本文设定OPLC是在环境温度为20℃条件下工作的, 导体半径为2.5mm, 外护套的厚度为2mm, 导体的热膨胀系数为0.55×10-6K-1, 光单元结构中光纤、外护套、阻水材料的导热系数分别为1.38W/(m·K),0.2W/(m·K),0.08W/(m·K)。一般情况下, 为避免短路故障造成过大的危害, 5s内必须断闸。正常工作稳态时和短路故障后5s时导体的温度是已知的, 分别达到70℃,160℃。假设稳态时, 离OPLC中心40mm处的空气温度与大气温度一致, 大小为20℃。OPLC外护套与周围环境之间属于自然对流, 取综合换热系数为11.6W/(m2·℃)。根据式(1)~(4), 利用以上边界条件、初始条件和多物理场仿真软件COMSOL[13]计算得到正常工作和突然短路后5s时的温度分布, 分别如图 1、图 2所示。并选取OPLC光单元上的一些特征点, 特征点分布如图 3所示。得到正常工作至稳态和突然短路5s期间特征点上温度变化曲线,分别如图 4、图 5所示。
|
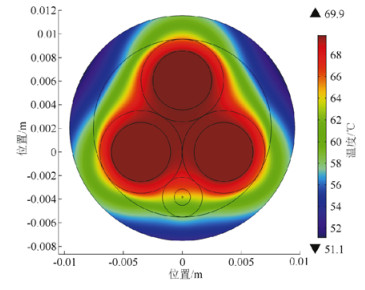
图 1 OPLC在稳定工作状态下的温度场分布 Fig. 1 OPLC temperature distribution in stable working condition |
|
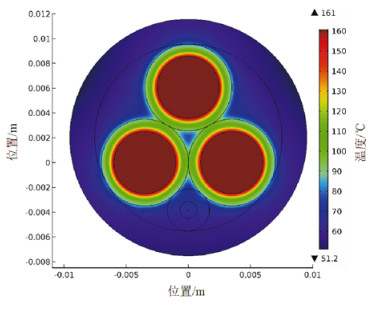
图 2 OPLC短路后5s的温度场分布 Fig. 2 OPLC temperature distribution after 5s of short circuit |
|
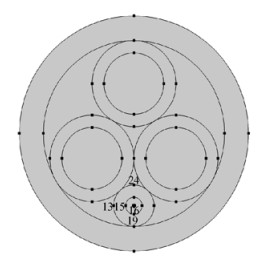
图 3 OPLC上光单元特征点分布 Fig. 3 Feature points distribution of OPLC optical element |

|
图 4 工作至稳态时光单元特征点温升曲线 Fig. 4 Temperature rise curves of optical-element feature points at steady state |
|
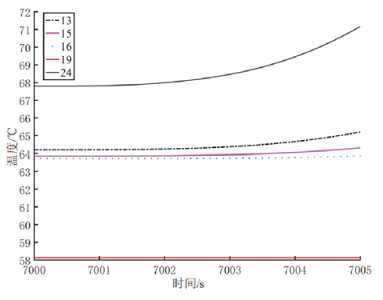
图 5 短路后5s期间光单元特征点温升曲线 Fig. 5 Temperature rise curves of optical-element feature points during 5s of short circuit |
从图 1可以看出, 经过一定时间后, OPLC铜导体的温度稳定在69.9℃。由OPLC中心向外, 温度逐渐降低。从图 4可以看出, 光纤上特征点15和16稳态时的温度为63.8℃。但是, 光单元外护套上不同位置处的温度却不同, 外护套上特征点13,19,24的温度差异很大, 其中特征点19温度最低。这是因为特征点19离铜导体更远, 所以温度比其他两处光单元外护套的温度低。
从图 2可以看出, 短路后, 导体温度急剧变化, 在5s内升高至161℃, 绝缘层的温度变化也很明显, 不同位置处绝缘层的温度由原来的分布不均趋于均匀。但是, 从图 5可以看出, 短路后5s光单元特征点的温度从内到外越来越低, 趋势逐渐变缓, 靠近铜导体的特征点24温度变化最剧烈, 而光纤特征点15和16的温度从稳态时的63.8℃升高至64.3℃, 只升高了0.5℃。这是因为导体敷设材料的导热系数比光纤和光单元外护套的小, 而短路仅5s后导体的温度变化还未传递至光纤处。
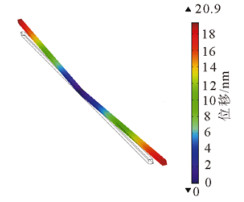
在正常工作和短路状态时, 温度升高使得光纤产生热膨胀, 从而改变光纤的热应力张量, 导致光纤发生形变。图 6、图 7分别为两种状态下长度为1.5cm光纤的形变位移图。
|
图 6 稳定状态时光纤形变位移图 Fig. 6 Fiber deformation displacement at steady state |
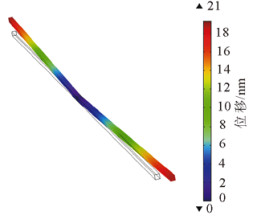
|
图 7 短路时光纤形变位移图 Fig. 7 Fiber deformation displacement after short circuit |
从图 6可以看出, 光纤在达到稳定状态时的最大形变位移量为20.9nm, 在径向光纤形变均匀分布, 这是因为光单元尺寸较小, 达到稳态时光纤沿直径方向的温度分布基本是均匀的。但是, 光纤在轴向上的形变有较大差异, 靠近光纤两端的部分形变较大, 从端部至中间形变量逐渐变小。从图 7可以看出, 铜导体短路后5s, 光纤的最大形变位移量达到21nm, 只比稳定状态增加了0.1nm。这是因为在短路后5s, 光纤温度比稳态时只升高了0.5℃, 对光纤的结构并没有大的影响。
2 OPLC的光纤传输特性从图 6和图 7可以看出, OPLC短路故障导致的瞬态温升没有使光纤的热变形明显增大。在上述仿真得到的光纤热变形的基础上, 进一步求解两种状态下光纤的传输特性, 研究OPLC短路故障对光纤传输特性的影响。
2.1 波动光学理论本文以阶跃单模光纤作为研究对象, 阶跃光纤中纤芯到包层的折射率是突变的, 当光线入射到纤芯和包层的交界面上时,会发生全反射而被限制在纤芯中传播[14]。光纤中的光波电磁矢量通过求解在均匀圆形介质波导边界条件下的麦克斯韦方程组得到[15-16]。因为光纤是圆柱形波导, 所以在柱坐标下求解。亥姆霍兹方程[17]在柱坐标系下可表示为
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}{\mathit{\boldsymbol{E}}_z}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {\mathit{\boldsymbol{E}}_z}}}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}{\mathit{\boldsymbol{E}}_z}}}{{\partial {\phi ^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{E}}_z}}}{{\partial {z^2}}} + k_0^2{n^2}{\mathit{\boldsymbol{E}}_z} = 0,\\ \frac{{{\partial ^2}{\mathit{\boldsymbol{H}}_z}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {\mathit{\boldsymbol{H}}_z}}}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}{\mathit{\boldsymbol{H}}_z}}}{{\partial {\phi ^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{H}}_z}}}{{\partial {z^2}}} + k_0^2{n^2}{\mathit{\boldsymbol{H}}_z} = 0 \end{array} \right.。$ | (10) |
其中, n为介质折射率, k0为自由空间中的波数,
| $ {\mathit{\boldsymbol{E}}_z} = AR\left( r \right)\mathit{\Phi }\left( \phi \right)Z\left( z \right)。$ | (11) |
导波沿光纤传播方向的变化规律为
| $ Z\left( z \right) = A{{\rm{e}}^{ - {\rm{j}}{\beta _z}}}。$ | (12) |
其中, βz表示传输方向的传播常数。导波在圆周方向按驻波规律变化为
| $ \mathit{\Phi }\left( \phi \right) = \left\{ {\begin{array}{*{20}{c}} {\cos \left( \phi \right)}\\ {\sin \left( \phi \right)} \end{array}} \right\}。$ | (13) |
对Ez应用分离变量法, 并将式(12)和(13)代入到式(10)中得到关于r的方程, 在纤芯n1和包层n2中分别表示为
| $ \left\{ \begin{array}{l} \frac{{{{\rm{d}}^2}R\left( r \right)}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}R\left( r \right)}}{{{\rm{d}}r}} + \left( {k_0^2{n_1}^2 - {\beta ^2}} \right) - \frac{{{1^2}}}{{{r^2}}}.\\ R\left( r \right) = 0,r \le a\\ \frac{{{{\rm{d}}^2}R\left( r \right)}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}R\left( r \right)}}{{{\rm{d}}r}} + \left( {k_0^2{n_2}^2 - {\beta ^2}} \right) - \frac{{{1^2}}}{{{r^2}}}.\\ R\left( r \right) = 0,r \ge a \end{array} \right. $ | (14) |
求解得R(r)之后,将R(r),Φ(ϕ),Z(z)带入式(11)中便可得到光纤传播方向的电场分量Ez, 表示为
| $ {\mathit{\boldsymbol{E}}_z} = {{\rm{e}}^{ - {\rm{j}}{\beta _z}}}\sin \left( \phi \right)\left\{ \begin{array}{l} {A_1}{J_1}\left( {{\rm{U}}{R_a}} \right),{R_a} \le 1\\ {A_2}{J_1}\left( {{\rm{W}}{R_a}} \right),{R_a} \ge 1 \end{array} \right. $ | (15) |
式中:U是导波径向归一化相位常数, 表征导波电场和磁场在纤芯横截面上的分布;W是导波径向归一化衰减常数, 表征导波电场和磁场在包层横截面上的分布;Ra表示归一化半径坐标,
同样, 可得到磁场矢量的z分量Hz。
| $ {\mathit{\boldsymbol{H}}_z} = B{{\rm{e}}^{ - {\rm{j}}{\beta _z}}}\cos \left( \phi \right)\left\{ \begin{array}{l} {A_1}{J_1}\left( {{\rm{U}}{R_a}} \right),{R_a} \le 1\\ {A_2}{J_1}\left( {{\rm{W}}{R_a}} \right),{R_a} \ge 1 \end{array} \right. $ | (16) |
对于其他4个横向分量Er,Eϕ和Hr,Hϕ,不能直接利用上述方程直接求解, 但是E和H的各个分量不是完全独立的, 可以利用这6个分量之间的关系求得[18-19]。
光纤求解时应满足的边界条件是:在纤芯的边界上, 场量的切向分量为连续[20-21], 即
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{E}}_{{\phi _1}}} = {\mathit{\boldsymbol{E}}_{{\phi _2}}},\\ {\mathit{\boldsymbol{H}}_{{\phi _1}}} = {\mathit{\boldsymbol{H}}_{{\phi _2}}},\\ {\mathit{\boldsymbol{E}}_{{z_1}}} = {\mathit{\boldsymbol{E}}_{{z_2}}},\\ {\mathit{\boldsymbol{H}}_{{z_1}}} = {\mathit{\boldsymbol{H}}_{{z_2}}}。\end{array} \right. $ | (17) |
实际使用中的光纤(尤其是单模光纤)都为弱波导光纤, 假设折射率分布为n(R), 电场在y方向振动并且沿z方向传播, 则电场[22]可表示为
| $ \mathit{\boldsymbol{E}} = {\mathit{\boldsymbol{E}}_0}\left( r \right){{\rm{e}}^{ - {\rm{j}}{\beta _z}}}。$ | (18) |
其中, βz是光纤沿z轴方向的传播常数。
设光纤弯曲半径为Rc, θ为偏离传输方向的角度。光纤的弯曲部分电场的变化量为e-jz(θ), 则弯曲光纤中的传播常数为
| $ \beta = {\beta _z}\left( {1 - r\cos R/{R_{\rm{c}}}} \right)。$ | (19) |
其中,
将式(19)代入式(14)得
| $ \begin{array}{l} \frac{{{{\rm{d}}^2}R\left( r \right)}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}R\left( r \right)}}{{{\rm{d}}r}} + \\ k_0^2{n^2}\left( r \right) - \beta _z^2{\left( {1 - r\cos \theta /{R_{\rm{c}}}} \right)^2} - \frac{1}{{{r^2}}}R\left( r \right) = 0。\end{array} $ | (20) |
由式(20)可得, 场沿着r的正方向偏移, 可以知道存在一个临界的xr>0, 当r>xr时, 则有k02 n2(r)-βy2 (1-rcosθ/Rc)2>0, 也就是电场沿着径向偏移, 使部分光波沿径向传播, 引起传输损耗。
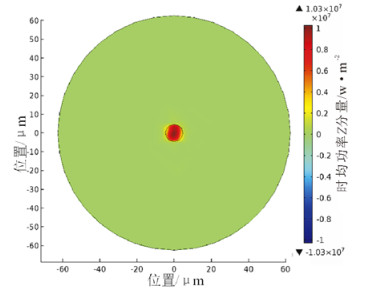
2.3 光纤传输特性仿真分析在上述光纤热形变仿真结果的基础上对光纤进行波动光学、固体力学耦合仿真, 进一步研究短路瞬态温升对光纤传输特性的影响。本仿真的模型参数设置为:纤芯半径4.6μm, 包层半径62.5μm, 纤芯和包层的折射率分别为n1=1.445 7, n2=1.440, 入纤功率为1mW, 波长为λ=1 550nm。如图 8和图 9所示,分别为仿真得到的两种工作状态下的时均功率Z分量。
|
图 8 正常工作状态光纤时均功率Z分量 Fig. 8 Average power Z component in optical fiber in steady state |
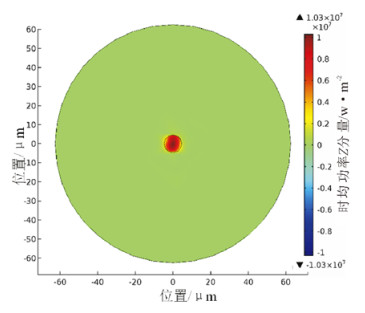
|
图 9 短路后5s光纤时均功率Z分量 Fig. 9 Average power Z component in optical fiber after 5s of short circuit |
坡印廷矢量是表征电磁波能流密度的物理量, 在COMSOL中用时均功率流表示, 通过对光纤时均功率Z分量在输出端口的面积分就可以得到光纤的输出功率。从图 8和图 9中可以看出, OPLC在正常工作和短路后5s, 光纤沿Z轴的时均功率分布几乎一样, 则光纤中的总功率为计算得到光纤的输出功率为P=0.992 2mW。
| $ \begin{array}{l} P = {P_1} + {P_2} = \\ {a^2}\int_0^{2{\rm{ \mathsf{ π} }}} {{\rm{d}}\phi } \int_0^1 {{S_z}{R_a}{\rm{d}}{R_a}} + {a^2}\int_0^{2{\rm{ \mathsf{ π} }}} {{\rm{d}}\phi } \int_1^\infty {{S_z}{R_a}{\rm{d}}{R_a}} 。\end{array} $ | (21) |
结合图 8和图 9时均功率流和上述计算结果, 短路引起的0.1nm的形变增加量对光纤传输特性影响轻微。这是因为电缆短路后5s时的温度相对于稳定状态时只变化了0.5℃, 光纤形变量也比稳态时只增加了0.1nm, 这时弯曲半径Rc非常大, 从式(19)可以看出, 对光纤的传播常数的影响几乎为0。所以, 短路虽然引起了OPLC缆温度的急剧升高, 但是没有进一步使光纤的传输特性恶化。
3 结语应用多物理场仿真软件COMSOL进行温度场、应力场和波动光学的耦合建模, 仿真结果表明:①在OPLC正常工作状态时, 光纤径向温度差别不大, 光纤径向形变均匀,轴向形变差别较大, 其中形变量在光纤两端达到最大; ②短路后的瞬间温升并没有使光纤的热形变量进一步显著增大, 只增加了0.1nm; ③两种工作状态下光纤沿传输方向的时均功率分布一致, 计算得到的输出功率也一致, 所以OPLC瞬时短路引起的瞬态温升并不影响光纤结构以及光纤的传输特性。
本文对工程实际中OPLC缆的设计与选型有一定的指导意义, 具有实际应用价值。
| [1] |
刘振亚. 智能电网技术[M]. 北京: 中国电力出版社, 2010.
|
| [2] |
范宏, 高亮, 周利俊, 等. 智能电网的电力光纤入户技术及其应用[J]. 电力自动化设备, 2013, 33(7): 149-150. DOI:10.3969/j.issn.1006-6047.2013.07.026 |
| [3] |
涂兴华, 倪彬, 李军博. 光纤复合低压电缆温度分布与光单元传输特性研究[J]. 量子电子学报, 2017, 34(1): 88-93. |
| [4] |
YAN K, HONG J, ZHANG J. Thermal-deformation coupling in the thermal network for transient analysis of spindle bearing system[J]. International Journal of Thermal Sciences, 2016, 104: 1-12. DOI:10.1016/j.ijthermalsci.2015.12.007 |
| [5] |
OHSAKI H, KUMAGAI D, TOMITA M. Thermal and cooling characteristic analysis of a superconducting DC power cable for railway application[J]. IEEE Transactions on Applied Superconductivity, 2015, 25(3): 1-5. |
| [6] |
GONZALEZ C, WECKX S, RYBEL T D, et al. Dynamic thermal modeling of voltage divider capacitive coupling[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1015-1025. DOI:10.1109/TPWRD.2015.2392386 |
| [7] |
WEN H, YANG F, LV W Q, et al. Finite element analysis of the temperature field of an emergency brake and study of its thermal properties[J]. Strength of Materials, 2015, 47(1): 136-142. DOI:10.1007/s11223-015-9639-x |
| [8] |
MOTES D K, WOMACK K, STEFANI F, et al. Thermal analysis of high-energy railgun tests[J]. IEEE Transcations on Plasma Science, 2012, 40(1): 124-130. DOI:10.1109/TPS.2011.2174375 |
| [9] |
CERIT M, COBAN M. Temperature and thermal stress anslyses of a ceramic-coated aluminum alloy piston used in a diesel engine[J]. International Journal of Thermal Sciences, 2014, 77(1): 11-18. |
| [10] |
许开城.锅炉汽包的热应力分析[D].吉林: 东北电力大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10188-1016183089.htm
|
| [11] |
王瑛, 施磊, 曹晓珑, 等. 交联聚乙烯电缆生产过程中热应力的计算[J]. 电线电缆, 2001(3): 14-16. DOI:10.3969/j.issn.1672-6901.2001.03.004 |
| [12] |
徐伟.基于材料匹配性的盘式制动片热-应力耦合场研究[D].武汉: 武汉理工大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10497-2009103239.htm
|
| [13] |
明平剑, 张文平. 计算多物理场:有限体积方法应用[M]. 北京: 北京航空航天大学出版社, 2015.
|
| [14] |
HE X, YI H, LONG J, et al. Plasmonic crystal cavity on single-mode optical fiber end facet for label-free biosensing[J]. Applied Physics Letters, 2016, 108(23): 3798. |
| [15] |
CHEN Y, HAN Q, YAN W, et al. Magnetic field and temperature sensing based on a macro-bending fiber structure and an FBG[J]. IEEE Sensors Journal, 2016, 16(21): 7659-7662. DOI:10.1109/JSEN.2016.2603521 |
| [16] |
LIU T, CHEN Y, HAN Q, et al. Magnetic field sensor based on u-bent single-mode fiber and magnetic fluid[J]. IEEE Photonics Journal, 2014, 6(6): 1-7. |
| [17] |
吴重庆. 光波导理论[M]. 北京: 清华大学出版社, 2005.
|
| [18] |
WU L, WANG Q, GUO M, et al. Characterization of displacement sensing based on fiber optic microbend losses[J]. Instrumentation Science & Technology, 2016, 44(5): 471-482. |
| [19] |
GARDNER W B. Microbending loss in optical fibers[J]. Bell Labs Technical Journal, 2014, 54(2): 457-465. |
| [20] |
ZHANG R, LIU T, HAN Q, et al. U-bent single-mode-multimode-single-mode fiber optic magnetic field sensor based on magnetic fluid[J]. Applied Physics Express, 2014, 7(7): 072501. |
| [21] |
ZHENG X, REN G, HUANG L, et al. Bending losses of trench-assisted few-mode optical fibers[J]. Appl Opt, 2016, 55(10): 2639-2648. DOI:10.1364/AO.55.002639 |
| [22] |
任健.抗弯曲损耗光纤及纳米结构型光纤的研究[D].南京: 南京邮电大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10293-1013168442.htm
|
 2018, Vol. 48
2018, Vol. 48