在对实际的金融数据进行分析的过程中, 学者们发现金融市场经常会受到一些突发事件的影响, 而使得金融数据在某个时刻k后, 样本的分布或分布参数缓慢地开始变化。在对金融数据进行建模时, 必须对渐变变点时刻进行检验。所以对均值渐变模型的变点检验也是统计学的研究热点。Jarušková(1998)[1]对随机误差项为独立同分布序列的均值渐变模型进行了对数似然比检验, 得出检验统计量的渐近分布为Gumbel分布; Hušková(1999)[2]对随机误差项为独立同分布序列的均值渐变模型进行研究, 得到变点估计量的收敛速度及其极限分布; Hušková与Steinebach (2000)[3]使用CUSUM方法对渐变变点进行检验, 得到检验统计量的极限分布; Alexander和Josef(2002)[4]研究随机误差项满足弱不变原理的渐变随机过程中变点的估计, 并给出变点估计量的收敛速度; Madurkayova(2007)[5]对随机误差为独立同分布序列的均值渐变模型运用RCUSUM函数的比率构造Ratio统计量, 进行单变点检验; Steinebach和Timmermann (2011)[6]研究了具有漂移项的随机过程中渐变变点, 并对其进行序贯检验; Timmermann (2014)[7]对渐变变点进行在线监测, 得到零假设和备择假设下检验统计量的极限分布; Vogt和Dette(2015)[8]研究了非参数模型中渐变变点估计量的渐近分布; Timmermann (2015)[9]研究了随机误差项满足弱不变原理的渐变随机过程, 得到序贯检验统计量的极限分布。对于长相依序列, 则有Wang Lihong和Wang Jinde[10]研究了带有长记忆性的移动平均模型(MA)中方差突变点的检测问题, 在均值已知的情况下得到了未知变点的估计量及估计量的收敛速度, 在均值未知的情况下得到原假设和备择假设下检验统计量的极限分布; Wang Lihong (2007)[11]给出随机误差为长相依序列的均值渐变变点的最小二乘估计量, 得到该估计量的收敛速度; Wang Lihong (2008)[12]研究了长记忆MA模型中均值变点问题。
检验渐变变点问题最常用的方法是累积和(CUSUM)方法, 然而现有的CUSUM检验在讨论检验统计量渐近性质时要求原假设与备择假设下对模型的尺度参数的估计应该是一致的。事实上, 在观察值独立的情况下, 对模型的尺度参数的估计也并不容易, 相依序列的情况就更为复杂。本文基于CUSUM函数的比率构造了Ratio统计量, 避免了CUSUM方法中的尺度参数估计, 得到了零假设和备择假设下检验统计量的极限分布。
1 Ratio统计量考虑如下均值渐变模型:
| $ {Y_i} = \mu + \delta \left( {\frac{{i - {k^ * }}}{n}} \right)_ + ^\gamma + {e_i},1 \le i \le n。$ | (1) |
其中k*为未知变点, a+=max(0, a), μ, δ≠0, γ∈[0, 1]均为未知参数。
假设
| $ {e_i} = \sum\limits_{j = 1}^\infty {{a_j}{\varepsilon _{i - j}}} $ | (2) |
其中, {εj, -∞ < j < ∞}为均值为0, 方差为1的独立同分布的随机变量组成的序列, 且
| $ \begin{array}{l} \sum\limits_{j = 1}^\infty {a_j^2} < \infty ,{a_j} \sim {c_0}{j^{d - 1}},j \to \infty ,\\ 0 < {c_0} < \infty ,0 < d < 1/2, \end{array} $ | (3) |
符号‘~’表示左边与右边的比率趋近于1。由文献[11]可知, 式(2),(3)定义的{ei}是带有长记忆性的线性平稳过程。
假设检验如下:
| $ {{\rm{H}}_0}:{k^ * } = n; $ |
| $ {{\rm{H}}_1}:{k^ * } < n,\delta \ne 0。$ |
考虑Ratio检验统计量
| $ {Z_n} = \mathop {\max }\limits_{\left[ {na} \right] \le k \le \left[ {n - na} \right]} \frac{{\mathop {\max }\limits_{k < i \le n} \left| {{{\tilde S}_{i,k}}} \right|}}{{\mathop {\max }\limits_{1 < i \le k} \left| {{{\bar S}_{i,k}}} \right|}}, $ | (4) |
其中[na]表示取整, 0 < a < 1/2是一个给定的常数, 且
| $ {{\bar S}_{i,k}} = \sum\limits_{j = 1}^k {\left( {{x_{ji}} - {{\bar x}_{i,k}}} \right){Y_j}} , $ |
| $ {{\tilde S}_{i,k}} = \sum\limits_{j = k + 1}^n {\left( {{x_{ji}} - {{\bar x}_{i,k}}} \right){Y_j}} , $ |
| $ {{\bar x}_{i,k}} = \frac{1}{k}\sum\limits_{j = 1}^k {{x_{ji}}} ,{{\tilde x}_{i,k}} = \frac{1}{{n - {k_j}}}\sum\limits_{j = k + 1}^n {{x_{ji}}} , $ |
| $ {x_{ji}} = \left( {\frac{{j - i}}{n}} \right)_ + ^\gamma 。$ |
定理1 假定Y1, …, Yn满足模型(1)且原假设H0成立, 有
| $ \begin{array}{l} {Z_n}\xrightarrow{d}\mathop {\sup }\limits_{\tau \leqslant t \leqslant 1 - \tau } \\ \frac{{\mathop {\sup }\limits_{t \leqslant s \leqslant 1} \left| {\int_s^1 {\gamma {{\left( {x - s} \right)}^{\gamma - 1}}B_d^ * \left( {1 - x} \right){\text{d}}x} - \frac{1}{{1 - t}}\frac{{{{\left( {s - t} \right)}^{\gamma + 1}}}}{{\gamma + 1}}B_d^ * \left( {1 - t} \right)} \right|}}{{\mathop {\sup }\limits_{0 \leqslant s \leqslant t} \left| {\int_s^1 {\gamma {{\left( {x - s} \right)}^{\gamma - 1}}{B_d}\left( {t - x} \right){\text{d}}x} - \frac{1}{t}\frac{{{{\left( {t - s} \right)}^{\gamma + 1}}}}{{\gamma + 1}}{B_d}\left( t \right)} \right|}} \\ \end{array} $ | (5) |
其中{Bd(t), 0≤t≤1}和{Bd* (t), 0≤t≤1}是相互独立的分数布朗运动, 且Bd* (t)=Bd (1)-Bd (t)。
证明 由文献[13]中式(2),(6)可得, 存在一个分数布朗运动{Bd(y):0≤y < ∞}, 0 < d < 1/2, 使得当0≤t≤1时, 有
| $ \sum\limits_{i = 1}^{\left[ {nt} \right]} {{e_i}\xrightarrow{w}\kappa {B_d}\left( {nt} \right)} $ | (6) |
其中κ是一个常数。
由文献[14]可知
| $ \begin{array}{l} \mathop {\lim \sup }\limits_{T \to \infty } \mathop {\sup }\limits_{0 \le t \le T - {a_T}} \mathop {\sup }\limits_{0 \le s \le {a_T}} {\beta _T}\left| {{B_d}\left( {t + s} \right) - } \right.\\ {\left. {{B_d}\left( t \right)} \right| \overset{{a.\;s.}}{=} 1} \end{array} $ | (7) |
其中
| $ {\beta _T} = {\left( {2{a_T}\left( {\log \frac{T}{{{a_T}}} + \log \log T} \right)} \right)^{ - 1/2}}, $ |
因此, 有
| $ \begin{array}{l} \mathop {\sup }\limits_{0 \le t \le T} \mathop {\sup }\limits_{0 \le y \le 1} \left| {{B_d}\left( {t + y} \right) - {B_d}\left( t \right)} \right| = \\ O\left( {{{\left( {\log T} \right)}^{1/2}}} \right){\rm{a}}.\;{\rm{s}}. \end{array} $ | (8) |
记i′=k-i+1, e′j=ek-j+1,
| $ \begin{array}{l} {{\bar S}_{i,k}} = \sum\limits_{j = 1}^k {\left( {{x_{ji}} - {{\bar x}_{i,k}}} \right){Y_j}} = \\ \sum\limits_{j = 1}^k {{x_{ji}}{Y_j}} - {{\bar x}_{i,k}}\sum\limits_{j = 1}^k {{Y_j}} = \\ \left( {\sum\limits_{j = 1}^k {{x_{ji}}{e_j}} + \mu \sum\limits_{j = 1}^k {{x_{ji}}} } \right) - \left( {{{\bar x}_{i,k}}\sum\limits_{j = 1}^k {{e_j}} + k\mu {{\bar x}_{i,k}}} \right) = \\ \sum\limits_{j = 1}^k {\left( {\frac{{j - i}}{n}} \right)_ + ^\gamma {e_j}} - \frac{1}{k}\sum\limits_{j = 1}^k {\left( {\frac{{j - i}}{n}} \right)_ + ^\gamma } \sum\limits_{j = 1}^k {{e_j}} 。\end{array} $ | (9) |
由文献[3]中式(2.14)类似可得
| $ \begin{array}{l} \sum\limits_{j = 1}^k {\left( {\frac{{j - i}}{n}} \right)_ + ^\gamma {e_j}} = \\ \sum\limits_{m = 1}^{i' - 1} {\left( {{{\left( {\frac{m}{n}} \right)}^\gamma } - {{\left( {\frac{{m - 1}}{n}} \right)}^\gamma }} \right)} \sum\limits_{l = 1}^{i' - m} {{{e'}_l}} \end{array} $ |
因此
| $ \begin{array}{l} {{\bar S}_{i,k}} = \sum\limits_{m = 1}^{i' - 1} {\left( {{{\left( {\frac{m}{n}} \right)}^\gamma } - {{\left( {\frac{{m - 1}}{n}} \right)}^\gamma }} \right)} \sum\limits_{l = 1}^{i' - m} {{{e'}_l}} - \\ \frac{1}{k}\sum\limits_{m = 1}^k {{{\left( {\frac{{m - i}}{n}} \right)}^\gamma }} \sum\limits_{j = 1}^k {{e_j}} = \\ \sum\limits_{m = 1}^{i' - 1} {\left( {{{\left( {\frac{m}{n}} \right)}^\gamma } - {{\left( {\frac{{m - 1}}{n}} \right)}^\gamma }} \right)\kappa {B_d}} \left( {i' - m} \right) - \\ \frac{1}{k}\sum\limits_{m = 1}^k {{{\left( {\frac{{m - i}}{n}} \right)}^\gamma }} \kappa {B_d}\left( k \right) + \\ {o_p}\left( {{{\left( {\frac{{k - i}}{n}} \right)}^\gamma }\left( {1 + \frac{{k - i}}{k}} \right)} \right), \end{array} $ | (10) |
其中i, k=1, …, n, i < k。
取k=[nt], i=[ns], 0 < s < t < 1, m′=m-[ns], 由式(8)及考虑分数布朗运动的性质, 可得
| $ \begin{array}{l} \sum\limits_{m = 1}^{i' - 1} {\left( {{{\left( {\frac{m}{n}} \right)}^\gamma } - {{\left( {\frac{{m - 1}}{n}} \right)}^\gamma }} \right){B_d}} \left( {i' - m} \right) = \\ \sum\limits_{m' = \left[ {ns} \right] + 1}^{\left[ {nt} \right]} {\left( {{{\left( {\frac{m}{n}} \right)}^\gamma } - {{\left( {\frac{{m - 1}}{n}} \right)}^\gamma }} \right){B_d}\left( {\left[ {nt} \right] - m' + 1} \right)} = \\ \int_{\frac{{\left[ {ns} \right] + 1}}{n}}^{\frac{{\left[ {nt} \right]}}{n}} {\gamma \left( {y - \frac{{\left[ {ns} \right]}}{n}} \right)_ + ^{\gamma - 1}{B_d}\left( {n\left( {t - y} \right)} \right){\rm{d}}y} + \\ {O_p}\left( {{{\left( {\frac{{\left[ {nt} \right] - \left[ {ns} \right]}}{n}} \right)}^\gamma }\sqrt {\log \left( {\left[ {nt} \right] - \left[ {ns} \right]} \right)} } \right), \end{array} $ | (11) |
| $ \begin{array}{l} \frac{1}{k}\sum\limits_{m = 1}^k {{{\left( {\frac{{m - i}}{n}} \right)}^\gamma }} {B_d}\left( k \right) = \\ \frac{1}{{\left[ {nt} \right]}}\sum\limits_{m = 1}^{\left[ {nt} \right]} {\left( {\frac{{m - \left[ {ns} \right]}}{n}} \right)_ + ^\gamma } {B_d}\left( {\left[ {nt} \right]} \right) = \\ \frac{n}{{\left[ {nt} \right]}}\int_0^{\frac{{\left[ {nt} \right]}}{n}} {\left( {\frac{{x - \left[ {ns} \right]}}{n}} \right)_ + ^\gamma {B_d}\left( {\left[ {nt} \right]} \right){\rm{d}}x} = \\ \frac{1}{t}\frac{{{{\left( {t - s} \right)}^{\gamma + 1}}}}{{\gamma + 1}}{B_d}\left( {\left[ {nt} \right]} \right) + \\ {O_p}\left( {\frac{{{{\left( {\left[ {nt} \right] - \left[ {ns} \right]} \right)}^{\gamma + 1}}\sqrt {\log \left( {\left[ {nt} \right]} \right)} }}{{\left[ {nt} \right]{n^\gamma }}}} \right), \end{array} $ | (12) |
上两式在s, t∈[0, 1], s≤t-
对于一个给定的k=[nt], 结合式(10)~(12), 有
| $ \begin{array}{l} \mathop {\sup }\limits_{0 \le s \le t} \left| {{\kappa ^{ - 1}}{{\bar S}_{i,\left[ {nt} \right]}} - \left( {\int_{\frac{{\left[ {ns} \right] + 1}}{n}}^{\frac{{\left[ {nt} \right]}}{n}} {\gamma \left( {x - \frac{{\left[ {ns} \right]}}{n}} \right)_ + ^{\gamma - 1}} } \right.} \right.\\ \left. {\left. {{B_d}\left( {n\left( {t - x} \right)} \right){\rm{d}}x - \frac{1}{t}\frac{{{{\left( {t - s} \right)}^{\gamma + 1}}}}{{\gamma + 1}}{B_d}\left( {nt} \right)} \right)} \right| = \\ {o_p}\left( 1 \right)。\end{array} $ | (13) |
类似地, 可得
| $ \begin{array}{l} \mathop {\sup }\limits_{0 \le s \le t} \left| {{\kappa ^{ - 1}}{{\bar S}_{i,\left[ {nt} \right]}} - \left( {\int_{\frac{{\left[ {ns} \right] + 1}}{n}}^1 {\gamma \left( {x - \frac{{\left[ {ns} \right]}}{n}} \right)_ + ^{\gamma - 1}} B_d^ * } \right.} \right.\\ \left. {\left. {\left( {n\left( {1 - x} \right)} \right){\rm{d}}x - \frac{1}{{1 - t}}\frac{{{{\left( {s - t} \right)}^{\gamma + 1}}}}{{\gamma + 1}}B_d^ * \left( {n\left( {1 - t} \right)} \right)} \right)} \right|\\ = {o_p}\left( 1 \right)。\end{array} $ | (14) |
结合式(13), (14), 可得定理结论。
定理2 假设Y1, …, Yn满足模型(1)且k*=[nt], 对任意的0 < t < 1, 有
| $ {n^{1/2}}\left| {{\delta _n}} \right| \to \infty , $ | (15) |
则在备择假设H1下, 对a < t < 1-a, 当n→∞时, 有
| $ {Z_n}\xrightarrow{P}\infty 。$ | (16) |
证明 取k=k*, i=k*。
| $ \begin{array}{l} {{\tilde S}_{{k^ * },{k^ * }}} = \sum\limits_{j = {k^ * } + 1}^n {\left( {{x_{j{k^ * }}} - {{\tilde x}_{{k^ * },{k^ * }}}} \right){Y_j}} = \\ \sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }{Y_j}} - \\ \frac{1}{{n - {k^ * }}}\sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }} \sum\limits_{j = {k^ * } + 1}^n {{Y_j}} = \\ \sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }\left( {\mu + \delta {{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma } + {e_j}} \right)} - \\ \frac{1}{{n - {k^ * }}}\sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }} \end{array} $ |
| $ \begin{array}{l} \sum\limits_{j = {k^ * } + 1}^n {\left( {\mu + \delta {{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma } + {e_j}} \right)} = \\ \sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }\delta {{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }} + \sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }{e_j}} - \\ \frac{1}{{n - {k^ * }}}\sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }\delta } \sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }} - \\ \frac{1}{{n - {k^ * }}}\sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }} \sum\limits_{j = {k^ * } + 1}^n {{e_j}} 。\end{array} $ |
对于n-1/2|
| $ \begin{array}{l} E\frac{{\left| {{{\tilde S}_{{k^ * },{k^ * }}}} \right|}}{{{n^{1/2}}}} \ge \left| {E\frac{{{{\tilde S}_{{k^ * },{k^ * }}}}}{{{n^{1/2}}}}} \right| = \\ \left| {\sum\limits_{j = {k^ * } + 1}^n {\frac{{{\delta _n}}}{{{n^{1/2}}}}{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^{2\gamma }}} - \sum\limits_{j = {k^ * } + 1}^n {{{\left( {\frac{{j - {k^ * }}}{n}} \right)}^\gamma }} } \right.\\ \left. {\frac{1}{{n - {k^ * }}}\sum\limits_{m = {k^ * } + 1}^n {\frac{{{\delta _n}}}{{{n^{1/2}}}}{{\left( {\frac{{m - {k^ * }}}{n}} \right)}^\gamma }} } \right| = \\ {n^{1/2}}\left| {{\delta _n}} \right|\left( {\frac{{\left( {n - {{\left[ {nt} \right]}^{2\gamma + 1}}} \right.}}{{{n^{2\gamma + 1}}}}\left( {\frac{{{\gamma ^2}}}{{\left( {2\gamma + 1} \right){{\left( {\gamma + 1} \right)}^2}}} + o\left( 1 \right)} \right)} \right) \end{array} $ |
上式中方括号内的表达式有非零的正极限。因此由式(15)可知当n→∞时
| $ E\left| {\frac{{{{\tilde S}_{{k^ * },{k^ * }}}}}{{{n^{1/2}}}}} \right| \to \infty , $ |
且
由于k=k*, n-1/2max1≤i≤k*|Si, k|与其在H0下的分布相同, 因此依概率有界, 所以当n→∞时,
定理1给出了原假设下检验统计量的极限分布, 定理2给出了备择假设下统计量依概率趋于无穷, 这说明当检验统计量的值大于临界值时拒绝原假设。
3 数值模拟及实例分析 3.1 数值模拟首先采用Monte Carlo方法对检验统计量Zn的极限分布进行数值模拟得到临界值。考虑到直接分析检验统计量Zn的极限分布较难, 本文采用检验统计量的样本分位数来近似检验统计量极限分布的分位数。
考虑如下数据生成过程:
| $ {Y_i} = \left\{ {\begin{array}{*{20}{c}} {\mu + {e_i},}&{1 \le i \le {k^ * },}\\ {\mu + \delta {{\left( {\frac{{i - {k^ * }}}{n}} \right)}_+^\gamma } + {e_i},}&{{k^ * } < i \le n,} \end{array}} \right. $ |
其中n为样本容量, k*为变点位置, ei为FARIMA(0, d, 0)过程。
首先验证d的变化对假设检验的影响, 取k*=n=1 000, μ=1, δ=2, γ=1, 取d=0.1, 0.2, 0.3, 0.4, 对每一个d, 分别对产生长度为1 000的FARIMA(0, d, 0)序列, 代入Zn可计算得一个值, 重复进行1 000次得到1 000个样本, 用该样本的分位点来近似统计量的极限分布的分位点, 得到检验统计量极限分布的α分位数, 如表 1。
|
|
表 1 检验统计量极限分布的α分位数 Tab. 1 α quantile of cimiting distribnt |
分别取样本容量n=500, 800, 1 000, μ=0, δ=2, γ=1, 重复进行1 000次试验, 检验水平α=0.05。模拟的经验水平和经验势函数值见表 2和表 3。同时运用文献[11]中所给的CUSUM检验的分位数, 模拟所得的经验水平和经验势函数值见表 2和表 3括号中的数值。
|
|
表 2 Zn的经验水平 Tab. 2 The empirical siye of Zn |
|
|
表 3 Zn的经验势函数值 Tab. 3 The emipirical power of Zn |
由表 2可知, 当d=0.1时, 样本容量n越大, Ratio检验统计量的检验水平越接近于0.05, 检测水平失真较小。同时, CUSUM检验的检验水平失真也较小。
由表 3可知, 当样本容量增加时, Ratio检验统计量经验势函数值也在增加, 而且样本容量越大, 经验势函数值越接近于1, 检验的效果越好。同时, 与CUSUM检验法相比, Ratio检验统计量的经验势函数值更接近1, 检验效果更胜一筹。
由表 2和表 3可知, d越大, 假设检验统计量的经验水平失真越小, 经验势函数值越接近于1。
然后,验证γ的变化对假设检验的影响。分别取样本容量n=500, 800, 1 000, μ=0, δ=2, d=0.1, γ=0, 0.25, 0.5, 0.75, 1, 重复进行1 000次试验, 检验水平α=0.05。模拟的经验水平和经验势函数值见表 4和表 5。同时运用文献[11]中所给的CUSUM检验的分位数, 模拟所得的经验水平和经验势函数值见表 4和表 5括号中的数值。
|
|
表 4 Zn的经验水平 Tab. 4 The empirical siye of Zn |
|
|
表 5 Zn的经验势函数值 Tab. 5 The empirical power of Zn |
由表 4可知, 当γ=1时, 样本容量n越大, Ratio检验统计量的检验水平越接近于0.05, 检测水平失真较小。同时, CUSUM检验的检验水平失真也较小。
由表 5可知, 当样本容量增加时, Ratio检验统计量经验势函数值也在增加, 而且样本容量越大, 经验势函数值越接近于1, 检验的效果越好。同时, 与CUSUM检验法相比, Ratio检验统计量的经验势函数值更接近1, 检验效果更胜一筹。
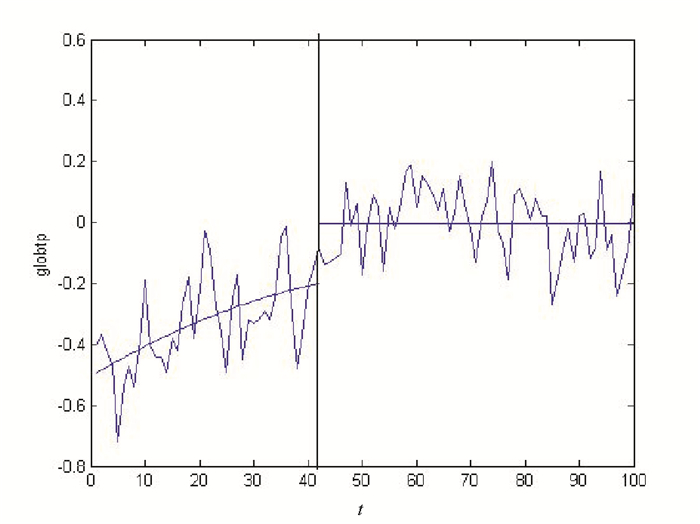
3.2 实例分析实例为验证Ratio检验法的有效性, 以全球平均温度为例, 分析从1880年到1980年的101个历史数据(数据来自http://www.datatang.com/data/3490), 首先得到原始数据的时序图, 如图 1所示。
|
图 1 全球平均温度时序图 Fig. 1 Global average temperature sequence diagram |
从图 1观察发现, 所选时间段间的数据呈现渐变的趋势, 可能存在变点。用本文的Ratio检验法, 假设检验如下:
| $ {{\rm{H}}_0}:{k^ * } = 101; $ |
| $ {{\rm{H}}_0}:{k^ * } < 101,\delta \ne 0。$ |
将所选数据带入检验统计量Zn中, 计算得到在α=0.05检验水平下, Ratio检验统计量Zn=1.198, 大于d=0.1, μ=0, δ=2, γ=1时对应的临界值0.305 7, 因此拒绝原假设, 也就是说所选时间段间的数据存在变点。
记时间1880年为t=1, 1881年为t=2, 一直到1980年为t=101, 运用最小二乘法估计出变点发生在t=42, 即1922年。从图 1可以看出, 1922年后全球平均温度呈上升趋势, 查阅相关资料, 猜测可能是工业革命以后, 人类大量使用化石燃料, 制造了大量二氧化碳等温室气体所造成的温室效应引起了全球平均气温的波动。
估计出变点位置后, 根据文献[15], δn的估计n, 以及μ的估计
| $ {{\hat \delta }_n} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_{i{k^ * }}} - {{\bar x}_{{k^ * }}}} \right){Y_i}} }}{{\sum\limits_{i = 1}^n {{{\left( {{x_{i{k^ * }}} - {{\bar x}_{{k^ * }}}} \right)}^2}} }}, $ |
| $ \hat \mu = {{\bar Y}_n} - {{\hat \delta }_n}{x_{{k^ * }}}。$ |
其中, 样本容量n=101, 变点位置k*=42, xik*=
| $ \begin{array}{l} {Y_i} = \\ \left\{ {\begin{array}{*{20}{c}} { - 0.001\;9 - 0.949\;0\left( {\frac{{42 - i}}{{101}}} \right) + {e_i},}&{1 \le i \le 42,}\\ { - 0.001\;9 + {e_i},}&{42 < i \le 101。} \end{array}} \right. \end{array} $ |
| [1] |
JARUŠKOVÁ D. Testing apperence of linear trend[J]. Journal of Statistical Planning and Inference, 1998, 70: 263-276. DOI:10.1016/S0378-3758(97)00184-5 |
| [2] |
HUŠKOVÁ M. Gradual changes versus abrupt changes[J]. Journal of Statistical Planning and Inference, 1999, 76: 109-125. DOI:10.1016/S0378-3758(98)00173-6 |
| [3] |
HUŠKOVÁ M, STEINEBACH J. Limit theorems for a class of tests of gradual changes[J]. Journal of Statistical Planning and Inference, 2000, 89: 57-77. DOI:10.1016/S0378-3758(00)00094-X |
| [4] |
ALEXANDER A, STEINEBACH J. A note on estimating the change-point of a gradually changing stochastic process[J]. Statistics and Probability Letters, 2002, 56: 177-191. DOI:10.1016/S0167-7152(01)00184-5 |
| [5] |
MADURKAYOVA B. Ratio tests for gradual changes[J]. Proceedings of Contributed Papers, 2007, 175-180. |
| [6] |
STEINEBACH J, TIMMERMANN H. Sequential testing of gradual changes in the drift of a stochastic process[J]. Journal of Statistical Planning and Inference, 2011, 141: 2682-2699. DOI:10.1016/j.jspi.2011.02.020 |
| [7] |
TIMMERMANN H. Monitoring procedures for detecting gradual changes [D]. Germany University of Cologne, 2014: 1-161.
|
| [8] |
VOGT M, DETTE H. Detecting gradual changes in locally stationary processes[J]. The Annals of Statistics, 2015, 43(2): 713-740. |
| [9] |
TIMMERMANN H. Sequential detection of gradual changes in the location of a general stochastic process[J]. Statistics and Probability Letters, 2015, 99: 85-93. DOI:10.1016/j.spl.2015.01.001 |
| [10] |
WANG Lihong, WANG Jinde. Change-of-variance problem for linear processes with long memory[J]. Statistical Paper, 2006, 47: 279-298. DOI:10.1007/s00362-005-0288-1 |
| [11] |
WANG Lihong. Gradual changes in long memory processes with applications[J]. Statistics, 2007, 41(3): 221-240. |
| [12] |
WANG Lihong. Change-in-mean problem for long memory time series models with applications[J]. Journal of Statistical Computation and Simulation, 2008, 78(7): 653-668. DOI:10.1080/00949650701216604 |
| [13] |
KUAN C. Change point estimation of fractionally integrated processes[J]. Journal of time series analysis, 1998, 19(6): 693-708. DOI:10.1111/jtsa.1998.19.issue-6 |
| [14] |
于德明. 分数布朗运动增量的一个泛函型极限定理[J]. 中国计量学院学报, 2001, 12(1): 37-41. DOI:10.3969/j.issn.1004-1540.2001.01.006 |
| [15] |
HUŠKOVÁ M. Estimation in location model with gradual changes[J]. Commentationes Mathematicae Universite Carolinae, 1998, 39: 147-157. |
 2018, Vol. 48
2018, Vol. 48