2. 延安大学 数学与计算机科学学院, 陕西 延安 71600
2. School of Mathematics and Computer Science, Yan′an University, Yan′an 716000, China
意大利数学家萨凯里(Girolamo Saccheri, 1667—1733)是非欧几何的重要先驱者之一, 他的工作将欧氏几何和非欧几何建立了联系。从欧几里得《原本》问世, 平行公设的证明就成为困扰数学家的难题, 许多数学家试图直接证明平行公设或寻找替代公设, 但都以失败告终。萨凯里尝试了证明平行公设的新途径, 提出直角、钝角和锐角假设, 按照《原本》传统的纯几何推理方式, 他得出直角假设与平行公设等价, 试图证明后两种假设存在矛盾而只有平行公设正确。虽然萨凯里也没有成功证明平行公设, 但他在锐角假设下得到的结论, 成为双曲几何的基本理论[1]。克吕格尔(S. Klügel, 1739—1812)批评了萨凯里的错误, 这引起兰伯特(J.H. Lambert, 1728—1777)的对萨凯里工作的重视。兰伯特利用代数方法提出了一些更具深远意义的非欧几何结论, 这使得数学家们开始怀疑除欧氏几何外的另一种几何的存在。
萨凯里四边形及锐角假设的主要结论在通史类文献中都有提及[2-5], 一些学者研究了萨凯里在推导锐角假设矛盾过程中的错误及原因, 他们认为萨凯里虽然得到了新几何的有趣结论, 但不愿意承认这些与直观相悖的结论, 并将其归咎于他维护欧几里得的决心[6-8]。直观或经验的因素是一方面, 更重要的是萨凯里逻辑学著作的影响。萨凯里究竟如何看待锐角假设的结论, 他错误的原因是什么, 他的工作为非欧几何的诞生起到了哪些奠基性作用, 这些问题对于萨凯里几何工作的合理定位, 认识非欧几何建立的思想来源, 了解非欧几何的早期历史都具有重要意义。本文将在萨凯里几何著作原始文献的基础上, 结合其逻辑证明著作, 试图解决以上历史问题。
1 萨凯里证明平行公设的出发点和逻辑方法1733年, 萨凯里的几何著作《免除所有污点的欧几里得》[8](Euclides ab Omni Naevo Vindicatus, 1733)出版(以下简称《免除》), 全书共有两卷, 第一卷证明平行公设, 包括39个命题以及若干推论和注释; 第二卷考察比和比例。萨凯里四边形以及锐角假设下的各种结论被认为是18世纪的几何杰作之一, 在非欧几何的建立和发展中扮演了重要角色。萨凯里用归谬法证明平行公设的唯一确定性, 试图解决平行公设独立与否的问题, 其动机与他关于逻辑和证明的工作息息相关。数学史研究的主要目的是回答历史上为什么会产生这样的数学[9], 因此很自然地提出下列问题, 萨凯里为什么要证明平行公设?他使用了什么方法?
在《免除》的前言部分, 萨凯里指出不同时代的数学家针对《原本》中若干“污点”的讨论, 包括平行公设缺乏显然性, 由证明平行公设产生的对平行线定义的争论, 即能否用等距直线定义平行线, 以及比例和复比的问题。萨凯里声明:
“在这本书中, 欧几里得几何的第一原则将被严格地证明……同时说明欧几里得的名望受到了不公正的抨击。”[8]
萨凯里证明平行公设的另外一个出发点是实践他早年著作《逻辑证明》(Logica Demostrativa, 1697)中提出的原则和方法。他在《逻辑证明》中考察了公理的一致性以及由定义得到的隐含条件, 这致使他对几何基础的进一步研究。萨凯里自己也称《逻辑证明》是他“智慧的结晶”(child of his genius)[10]。
《逻辑证明》为萨凯里提供了证明平行公设的方法。萨凯里认为即使是不证自明的公理也需要证明, 且公理一定能够证明, 而证明公理的最好方法就是绝妙推理(consequentia mirabilis)[11]。绝妙推理是从命题结论的否定出发的论证方法, 如果命题可以由其否定推导得出, 那么该命题为真, 即(﹁P→P)→P。绝妙推理与归谬法(reductio ad adsurdum)类似, 都是先假定命题的否定成立, 然后在此基础上推导; 二者的区别在于, 归谬法只需要推导的结论与公理, 前提假设, 或已证明的命题三者之一矛盾即可, 而绝妙推理要求最终得出的结论必须是命题本身, 因此并不具有普适性。1573年, 克拉维乌斯在《原本》的修订本中指出, 欧几里得在第九卷的命题12①中使用了绝妙推理[12]。该修订本启发萨凯里试图证明平行公设是公理, 并为他提供了绝妙推理的证明方法。他认为不论证明过程有多长, 用到多少定理, 只要从公理的反面出发得到公理本身, 就证明了公理。因此, 萨凯里的目的是使用绝妙推理证明平行公设不是定理, 而是一个公理, 从而说明欧几里得并没有错。
① Eu9.12:已知p为任意素数, a为自然数, 若p|an, 那么p|a.欧几里得的证明用现代语言表示为:假设p不整除a, 即p与a互素, 因为p|an=an-1·a, 所以p|an-1, 同理, p整除an-2, an-3…a.所以p整除a.
萨凯里首次使用绝妙推理检验几何公设, 也是第一个考虑一组公设中各公设独立性和相关性的数学家[13]。他在《免除》中大量使用该方法, 并在第一卷的结语中写道:
“我如此热切地证明每个不真的假设的矛盾……是因为每个原本真实的命题都有这样的特点, 假设其否定为真, 一定能通过完美的绝妙推理最终回到命题本身。我承认这是我早年在《逻辑证明》中对一些真命题研究的结果。”[8]
综合以上, 萨凯里证明平行公设的外在目的是为欧几里得辩护, 更深层次的目的是使用《逻辑证明》的原则和方法检验几何公理的独立性, 从而在几何上实践他提出的证明方法论。
2 萨凯里在锐角假设下得到的重要结论和证明漏洞萨凯里使用绝妙推理即假设命题的否定成立而推出命题本身, 结合归谬法来证明平行公设。首先, 萨凯里引入一个双直角等腰四边形ABCD, 其中AC与BD相等并垂直于底边AB(如图 1), 用《原本》第I卷的命题4和命题8可证明两顶角相等, 并且顶角为直角时线段AB等于CD, 顶角为钝角时线段AB小于CD, 顶角为锐角时线段AB大于CD。这三种情况分别对应着直角假设、钝角假设或锐角假设。
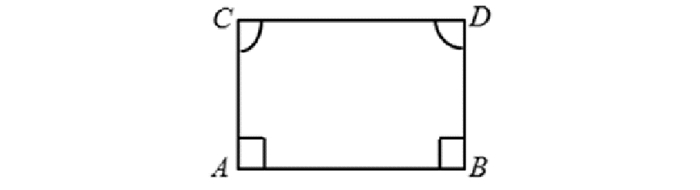
|
图 1 萨凯里四边形 Fig. 1 Sacchrei Quadrilateral |
根据萨凯里的逻辑证明方法, 他一方面要用绝妙推理证明平行公设成立, 另一方面证明钝角假设和锐角假设不成立。首先, 结合《原本》第Ⅰ卷前28个命题, 萨凯里证明了在直角假设和钝角假设下, 两条直线被第三条直线所截, 若形成的同旁内角小于两直角, 那么这两条直线一定会在有限处相交。而在钝角假设下的这一结论最终推导出三角形两内角之和大于两直角, 这与《原本》第Ⅰ卷命题17(在任何三角形中, 任意两角之和小于两直角)矛盾, 因此钝角假设不成立。其次, 与前两种假设的证明方式相同, 萨凯里试图说明在锐角假设中上述两直线在无限延伸后的相交情况, 得出两直线在无限远处相切, 但这与直线的自然特性矛盾, 因此锐角假设也不成立。萨凯里又用五个引理说明直线的自然特性包括两条直线不能包围一块空间; 两条直线不能有公共线段等。证明公理的绝妙推理是从命题的否定推出命题本身, 而萨凯里前面的证明是归谬法, 只能说明平行公设是一个定理。因此, 在最后的6个命题中, 萨凯里从等距直线的角度重新证明锐角假设和钝角假设的矛盾, 试图证明平行公设是公理。
萨凯里运用巧妙的假设技巧, 通过严谨的推理, 得到了一些重要的非欧几何基本结论, 但与此同时, 证明中的漏洞和谬误导致他对这些结论的错误判断。
2.1 锐角假设的重要结论萨凯里用纯几何推理的方式证明了非欧几何的基本结论, 例如, 任意三角形(四边形)内角和在直角、锐角、钝角假设下分别等于、小于、大于两直角(四个直角); 若3种假设之一在一个图形中成立, 那么在所有图形中都成立, 现在被称为萨凯里-勒让德定理。在锐角假设下, 当两条直线被第三条直线所截, 形成的同旁内角之和小于两直角时, 要么在有限处相交, 要么在无穷远处彼此接近(渐近直线); 两条直线在无穷远处要么在某点相切, 要么在该点有公垂线。这些结论触及到了双曲空间的性质, 被认为代表萨凯里几何工作的最高点[8]。作为前面结论的总结, 萨凯里在《免除》的命题32中叙述如下:
在锐角假设下, 有一个确定的锐角BAX决定了AX与BX仅在无限远处相遇(meet), 因此AX部分是内极限(intrinsic limit), 部分是外极限(extrinsic limit); 一方面, 所有与AB所成角小于角BAX的直线都与BX在有限处相交, 另一方面, 所有与AB所成角大于角BAX但小于等于直角的直线都与BX在不同的两点处具有公垂线[8]。
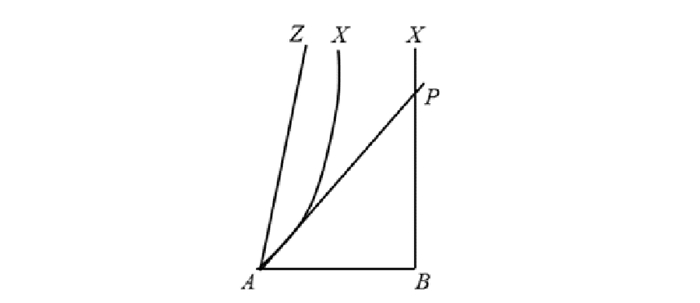
|
图 2 命题32 Fig. 2 Proposition 32 |
可以看出, 这个命题与罗巴切夫斯基(N. Lobachevsky, 1792—1856)对平行线的定义不谋而合。罗氏将平行线定义为过直线外一点与已知直线的相交线和不相交线的边界[14]。极限线AX事实上就是罗氏的平行线, 位于AX上方的线与BX不相交(超平行), 位于AX下方的线都与BX相交。
2.2 萨凯里的证明漏洞首先, 萨凯里在钝角假设推出的结论与《原本》第Ⅰ卷的命题17矛盾, 而欧几里得在证明这两个命题时默认了直线可以无限延长且可以延长到任意长度, 这个原理在当时是具有争议的, 萨凯里自己也意识到这一点, 因此, 他在《免除》的前言中强调, 他仅在有界的三角形中使用了这两个命题。萨凯里的证明本身是严格的, 钝角假设对应的几何模型是球面几何或椭圆几何, 而这两种几何中直线都是有限长且命题16并不成立[8], 因此萨凯里在默认命题16-17的前提下自然很容易就推出钝角假设的矛盾。但由于它们在锐角假设下成立, 类似的矛盾不能同样容易地推出, 所以他用了大量篇幅去推翻锐角假设。
其次, 锐角假设与直线的自然特性矛盾并不具有说服力。在命题33中断言AX和BX将在无限远处相遇, 要么相切且在切点处有公垂线, 要么彼此汇合成为一条直线。因此他称这些结论与直线的自然特性不相容(repugnant), 所以锐角假设自相矛盾。这里, 他错误地将无穷远点看作是有限处的点, 从而假设两条直线在无穷远处的某点相遇后可以继续延长。另外, 从逻辑证明的角度, 萨凯里对直线自然特性的“证明”因为经验的影响并不是绝对正确的结论, 因此与直线自然特性矛盾并不能作为锐角假设错误的依据。
第三, 萨凯里使用绝妙推理时出现的数学错误。在《免除》第一卷的最后6个命题中, 萨凯里考虑了与已知线段AC等距的点的连线。根据锐角假设的基本命题, 不断二等分CD与AB, 连接对应的中点, 得到的一系列垂线段都小于AC, 且垂线段的长度随着与AC或BD的接近而增加。将这些垂线段延长使得各自的长度等于AC或BD, 垂线段端点的连线, 或与AB距离相等的点D的运动轨迹就是曲线CKD(如图 3)。萨凯里证明了曲线CKD上的每一点都存在唯一的切线, 他利用切线的微元近似代替曲线的微元, 并认为切线的微元与底边AB的微元相等, 从而曲线CKD与底边AB长度相等。
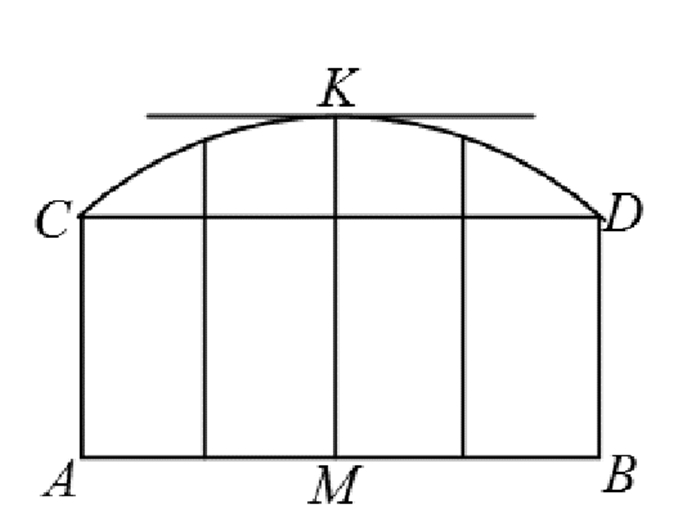
|
图 3 命题37 Fig. 3 Proposition 37 |
“…确定无疑的是, 切线的无穷小量K既不会大于也不会小于, 而是完全等于底边AB的无穷小量M, 因为显然可以假设线段MK是由点M到K的匀速运动的轨迹…”[8]
这样, 由于CKD大于弦CD, 那么AB大于CD, 这与锐角假设下AB小于CD矛盾, 即推出了锐角假设的否定。虽然上述过程满足绝妙定理的要求, 要证明﹁P, 假设P成立, 最后推出﹁P, 即(P→﹁P)→﹁P, 但萨凯里犯了一个错误, 即具有无穷小宽度的垂线MK将曲线CKD与底边AB对应地分割为不同的点, 从而曲线和直线上的点一一对应, 又因为它们都是点, 因此曲线和直线等长。萨凯里将线段上的点当作实无穷小量, 是一个明显的数学错误。
由于逻辑和数学上的错误, 萨凯里并没有得出锐角假设的矛盾。尽管如此, 他第一次结合《原本》中不需要平行公设的28个命题, 从命题的否定出发证明命题本身; 更重要的是, 在为欧几里得辩护的过程中, 他原创性地证明了另外两种几何即双曲几何和椭圆几何的基本结论, 为非欧几何的诞生奠定了基础。
3 萨凯里几何工作的影响萨凯里对非欧几何的创立者产生了重要影响, 他首次将几何分为3个分支并详细论述各种几何的基本理论。他在《免除》中使用正确的逻辑证明方法得出双曲几何创立所需要的基本结论, 他证明的错误进一步触及到了公理化方法以及数学的本质。第一次从数学的角度研究萨凯里平行线思想的是克吕格尔, 在1763年的毕业论文中, 他综述了前人的30多种对平行公设的证明, 用七分之一的篇幅叙述了萨凯里的证明, 并指出萨凯里证明的错误:“……如果这样的话, 任意曲线经过同样的方式被底边上的垂线逐次二等分, 都可以等于底边。”[8]克吕格尔的综述是萨凯里几何思想传播和演进的关节点, 引起同时代数学家对萨凯里几何工作的关注。
3.1 对同时代数学家的影响兰伯特通过克吕格尔的文章了解到萨凯里证明平行公设的主要步骤和重要定理。1766年, 兰伯特完成了著作《平行线理论》[15](Theorie der Parallellinien, 1786)。他接纳了代数方法和三角函数理论, 得到了一些更加深刻的非欧几何理论, 例如, 在锐角假设下存在长度的绝对度量, 锐角假设在虚半径球面上成立等。对于萨凯里的数学错误, 兰伯特提出在锐角假设下, 与底边AB等距点的连线的长度取决于距离AC的大小, 这在当时是十分先进的观点。
兰伯特的工作扩大了萨凯里平行线思想在欧洲的传播范围, 但也减少了数学家对《免除》的关注。虽然18世纪末到19世纪初的数学迅速向前发展, 但数学家仍然在关注作为几何基础的平行公设的证明。高斯(C.F.Guass, 1777—1855)、罗巴切夫斯基和波约(J. Bolyai, 1802—1860)都尝试了证明平行公设, 但最终都转向对锐角假设下的几何即双曲几何的研究。萨凯里和兰伯特的平行线思想和理论是他们研究的起点。例如, 罗巴切夫斯基将平行线定义为渐近直线, 并用解析方法讨论了萨凯里四边形的边角关系等。
在1830年到1860年之间, 萨凯里的工作很少被提及, 最多是出于收集资料的目的被收录在文选中。1889年, Manganotti神父重新发现了萨凯里的书并将其送给贝尔特拉米(Beltrami, 1835—1900)[5]。贝尔特拉米研读后写了一篇重要的文章, 说明萨凯里是罗巴切夫斯基和波约的先驱者。这引来了学者对萨凯里的大量研究, 探究他的工作对非欧几何的意义, 他的全部著作以及历史影响。1895年, F. Engel和P. Stäckel的《平行线理论:从欧几里得到高斯》收录了《免除》第一卷的德文版; 1920年, G.B. Halsted出版了《免除》的英文版。作为非欧几何的先驱者, 萨凯里的工作逐渐被后世所知。
3.2 现代数学史家的评价萨凯里的工作对非欧几何创立的重要意义是所有数学史家都认同的, 正如数学史家M.J. Greenberg的比喻, 萨凯里发现了钻石, 但他不相信自己看到的而声称它是玻璃[3]。锐角假设本身没有矛盾, 而由于对无穷和基数的误解他得出锐角假设自相矛盾的错误论断。在很大程度上, 这个错误引起了当时数学家对萨凯里平行线思想的进一步探讨, 对非欧几何的创立具有重要意义。另外, 对于17世纪末到18世纪的数学家来说, 犯这样的错误是有些出乎意料的, 因此许多数学史家都探讨了萨凯里错误的原因。
数学史家将萨凯里错误的原因归结为:首先, 萨凯里的出发点是为欧几里得辩护, 在证明之前就有平行公设是唯一正确的信念[6];其次, 几何在当时既是数学研究的一部分, 也是描述物理空间的学科, 经验阻碍了萨凯里对锐角假设结论的认同[7];第三, 萨凯里在证明中坚持使用综合几何的方法, 导致他错过新几何的发现[8]。事实上, 从萨凯里的证明步骤以及对前人的批评可以看出, 他对证明的逻辑严格性要求极高, 不可能承认一个未被严格证明的结论。在《逻辑证明》中萨凯里已经讨论了关于几何连续统无限可分的亚里士多德学派和芝诺悖论, 他一方面认为如果存在一个无限可分的连续统, 那么它一定可以真实地分割(即实无穷), 另一方面又认为点可以无限分割[13]。他在《逻辑证明》中对无穷的迷惑为平行公设证明的错误埋下了种子。萨凯里用切线微元近似代替曲线微元说明他对风靡当时的微积分方法并非一无所知, 他对无穷小的深入讨论也表明当时一些数学家开始对微积分基础的质疑。因此, 可以看出萨凯里不会为了说明欧几里得正确而不承认锐角假设的结论, 而是完全相信自己已经推导出锐角假设的矛盾。
4 结语萨凯里为了在几何上实践其《逻辑证明》的思想和方法, 利用综合几何的方法证明欧几里得平行公设的独立性。对无穷和基数错误理解以及对几何的有限认识, 导致萨凯里对锐角假设产生错误的见解, 但严谨的推理以及批判性思维, 使得他推导出了非欧几何的基本结论。结合其几何工作的目的和方法, 我们可以发现, 萨凯里并非为了说明平行公设唯一正确而不愿意承认锐角假设的结论, 他坚信自己用绝妙推理证明了锐角假设自相矛盾, 从而认为自己已经证明了平行公设。数学史上的许多重大发现都不是个别数学家灵机一动的结果, 而是建立在对前人工作继承和改进的基础上, 当然, 其中也包括前人工作的错误, 如非欧几何的先驱萨凯里。
| [1] |
莫里斯·克莱因.古今数学思想(第三册)[M].万伟勋, 石生明等译.上海: 上海科学技术出版社, 2014: 49.
|
| [2] |
GRAY J. Worlds out of Nothing: A Course in the History of Geometry in the 19th Century[M]. Springer London, 2007: 81-84.
|
| [3] |
BONOLA R. Non-Euclidean Geometry: A Critical and Historical Study of its Development[M]. Dover Publications, 1955: 22-44.
|
| [4] |
GREENBERG M J. Euclidean and non-Euclidean geometries: Development and History[J]. Whfreeman & Cosan Francisco Calif, 1973, 154. |
| [5] |
卡茨.数学史通论(第二版)[M].李文林, 邹建成等译.北京: 高等教育出版社, 2004: 485-488.
|
| [6] |
FITZPATRICK. Saccheri, forerunner of non-Euclidean geometry[J]. Mathematics Teacher, 1964, 57(5): 323-332. |
| [7] |
DOU A M. Logical and historical remarks on Saccheri′s geometry[J]. Notre Dame Journal of Formal Logic, 1974, 11(4): 385-415. |
| [8] |
SACCHERI G.Euclides ab Omni Naevo Vindicatus[M].Edited and annotated by Vincenzo De Risi.Translated by G.B.Halsted and L.Allegri.Springer International Publishing, 2014.
|
| [9] |
曲安京. 中国数学史研究范式的转换[J]. 中国科技史杂志, 2005, 26(1): 50-58. DOI:10.3969/j.issn.1673-1441.2005.01.008 |
| [10] |
PAGLI P. Two Unnoticed Editions of Girolamo Saccheri′s logica Demonstrativa[J]. History and Philosophy of Logic, 2009, 30(4): 331-340. DOI:10.1080/01445340903102490 |
| [11] |
EMCH A F. The Logical Demonstrativa of Girolamo Saccheri[D].Boston: Harvard University, 1934.
|
| [12] |
NUCHELMANS G. A 17th-century debate on the consequentia mirabilis[J]. History and Philosophy of Logic, 1992, 13(1): 43-58. DOI:10.1080/01445349208837193 |
| [13] |
LINDA A.The Mathematical Works of Girolamo Saccheri, S.J.(1667~1773)[D].New York: Columbia University, 1960.
|
| [14] |
LOBACHEVSKY N.Geometrical Researches on the Theory of Parallels[M]. Translated by George Bruce Halsted.Open Court Publishing Co., 1914: 13.
|
| [15] |
LAMBERT J H.Theorie der Parallellinien[M].Edited by Friedrich Engel and Paul Stäckel, //Urkunden zur Geschichte der Nichteuklidischen Geometrie. Leipzig, 1895: 137-208.
|
 2018, Vol. 48
2018, Vol. 48