【主持人语】 三支决策(Three-way decisions,3WD)是一种基于人类认知的决策模式,它把待解决的问题或待处理的信息分解为三个元素或者三个部分,进而再行处理。因其思想的朴素性与实用性,三支决策理论普遍存在于生活的各个方面。加籍华人姚一豫教授于2012年提出了较为完整的三支决策理论与思想方法,现已成为知识发现领域的研究热点,以及指导科学研究的方法论。
粒计算(Granular computing,GrC)是1997年由模糊数学之父Zadeh与林早阳教授提出的一个研究课题,是一种看待客观世界的世界观和方法论。其主要思想是采用粒度思想解决复杂问题,把复杂问题抽象、划分,从而转化为若干较为简单的问题的求解过程的理论、方法、技术以及工具等。
粗糙集理论(Rough set theory,RS)是波兰数学家Pawlak于1982年提出的一种数学理论,用于分析不可定义概念及其近似,是一种研究和处理不精确、不一致、不完整等各种不完备信息的有效的数学工具。
形式概念分析理论(Formal concept analysis,FCA)是德国数学家Wille于1982年为构建格理论应用语义而提出的。该理论对哲学中的“概念”这一人类思维的基本单元进行了形式化表达,进一步又形成概念格这一核心数据结构,以进行知识的可视化表示。形式概念分析与三支决策理论的结合诞生了三支概念分析(Three-way concept analysis,3WCA),是概念认知的又一种新思想。
本次专栏主要针对知识发现领域中的一些问题进行研究,包括如何从三支决策角度看待形式概念分析、粗糙集与粒计算,知识与数据双驱动的粒认知计算模型,三支决策空间上三支决策评价函数的构造,以及基于粗糙集的多粒度数据处理模型等四个方面的内容。这些工作既有对已有相关成果的总结与分析,也有针对热点问题的进一步讨论与新成果展示。这些研究内容都将为三支决策、粒计算以及知识发现领域的进一步研究打下基础。在此,主持人谨代表本次专栏全体作者向《西北大学学报》(自然科学版)表示诚挚的感谢。
主持人:魏玲,西北大学数学学院教授,博士生导师。
2. 西安电子科技大学 计算机学院,陕西 西安 710071;
3. 西北大学 数学学院, 陕西 西安 710127
2. School of Computer Science & Technology, Xidian University, Xi′an 710071, China;
3. School of Mathematics, Northwest University, Xi′an 710127, China
在知识发现研究领域, 近年来产生了很多有效的理论与方法, 无论是理论研究还是应用研究, 都有很多好的成果。比较热门的几个理论当属三支决策、粗糙集、形式概念分析与粒计算。其中, 三支决策与粒计算更强调方法性与思想性, 而粗糙集与形式概念分析则研究较为具体的工具。
在大家所熟知的二支决策模型中, 一般仅考虑接受与拒绝两种选择:不接受等同于拒绝, 不拒绝等同于接受。但在实际应用中往往并非如此。Yao提出的三支决策理论(Three-way decisions, 3WD)为此种情况提供了一个不同于接受与拒绝的第三种选择:不承诺[1-3]。
三支决策最初的思想是一种基于接受、拒绝和不承诺的三分类。其目标是将一个论域分为两两互不相交的3个部分, 这3个区域在一个具体的决策问题中可以分别被看作是接受域、拒绝域和不承诺域。相应于这3个区域, 可以建立三支决策规则。
进一步研究表明, 三支决策有更广义的解释和理解。三支决策是三元或三值思维, 采用3个选项, 从而走出了经典的二值、二元或两极思维的圈子和制约, 使我们能将对/错、好/坏、黑/白、左/右、上/下、过去/将来等扩展为对/中/错、好/中/坏、黑/灰/白、左/中/右、上/中/下、过去/现在/将来等。
事实上, 我们在日常生活中经常会用到三支决策的思想与方法。比如, 人事管理中的老、中、青3个梯队; 对某种观点的接受、拒绝和中立的态度; 投票中的赞成、反对和弃权选项; 按照短期、中期和长期目标制定计划; 医疗中关于治疗、进一步观察或者放弃治疗的决定; 论文评审过程中接收、拒稿或者返修再审等等。这些不胜枚举的例子说明, 人类认知与解决问题常常依赖于这样的三分类方法。因此, 三支决策的思想早已为大家所认可, 且被非常自然地广泛应用于许多研究领域。到目前为止, 三支决策研究的主流是构建理论和数学模型、探索三支方法和应用[2-11]。广义三支决策的主要思想是以三为本, 基三思维, 用三而治, 是基于“三”的思维方式、问题求解方法和信息处理模式, 是三元论和三分法。
粗糙集理论(Rough set theory, RS)是波兰数学家Pawlak于1982年提出的一种分析数据的数学理论, 用于分析不可定义概念及其近似[12], 是一种研究和处理不精确(imprecise)、不一致(inconsistent)、不完整(incomplete)等各种不完备信息的有效的数学工具。1991年Pawlak关于粗糙集的第一部专著的问世, 标志着粗糙集理论及其应用的研究进入了活跃时期[13]。
粗糙集在处理不确定性和不精确问题方面都推广了经典集合论, 可以用来描述知识的不完备性。从知识描述的方法上来看, 粗糙集理论研究可定义概念(即可描述集合)和不可定义概念, 通过一对可定义概念给出一个不可定义概念的上、下近似; 从集合中对象间的关系看, 粗糙集强调的是集合对象间的不可分辨; 从研究对象的角度看, 粗糙集研究的是不同类中的对象组成的集合之间的关系, 重在分类[14-18]。
形式概念分析理论(Formal concept analysis, FCA)是德国数学家Wille于1982年为构建格理论应用语义而提出的[19]。自1982年第一篇论文问世, 到1999年第一本专著出版, 标志着形式概念分析理论的初步完善[20]。
形式概念分析理论从限定一个“背景”开始, 给出对象集合与属性集合的元素之间的二元关系, 即所谓的“形式背景”; 进而, 用集合论的语言描述和建造概念, 包括基本的导出算子、内涵与外延、形式概念、概念格等。该方法将“概念格”作为基础, 讨论在背景和概念层次分析的框架下, 如何来研究格的结构与表示理论。
形式概念分析理论最根本的贡献和核心是对概念的数学化和形式化的描述, 以及以此为基础形成的格结构。形式概念分析近年来的发展无论在理论还是在应用上都有了自己的一套方法, 成为了一个新的有影响力的研究方向。近年来形式概念分析蓬勃发展的趋势离不开其他相关理论的支撑和互补, 比如粗糙集、粒计算、模糊集等[21-27]。形式概念分析已经应用到诸如信息检索、语义Web、知识工程等很多领域。
粒计算(Granular computing, GrC)是1997年由模糊数学之父Zadeh与林早阳教授提出的一个概念[28], 目前尚无明确的定义, 不同的研究者对这个概念及其相关研究领域有不同的理解。但是, 一个公认的观点是:粒计算是一种看待客观世界的世界观和方法论, 其主要思想是采用粒度思想解决复杂问题, 把复杂问题抽象、划分, 从而转化为若干较为简单的问题的求解过程的理论、方法、技术以及工具等多个方面[29-36]。
实际上, 粒就是指一些个体通过相似关系、邻近关系或功能关系等所形成的块。这种获得粒的过程就是信息粒化。粒化, 是问题空间的一个划分过程, 它可以简单理解为在给定粒化准则下(如等价关系)的一个分层的过程, 是粒计算的基础。通过粒化, 我们可以得到问题空间的层次内部、以及层次之间的结构。我们平日所说的分门别类、化整为零的思想, 就是粒计算思想的一种体现。
本文针对知识发现领域中目前流行的FCA, RS以及GrC三种理论与方法, 从三支决策的角度对它们的思想进行提炼和分析, 并揭示它们之间的联系。
1 三支决策研究方法三支决策的主要思想是3分而治, 是将一个整体分为3个部分, 并采用有效的策略处理这3个部分, 即三分与治略。
三分而治中“三”的选择是基于心理学和认知科学的一个重要结论。早在1956年, Miller的研究显示, 由于受到短期记忆的限制, 我们每个人只能处理7个单元左右的信息[37]。三划分给出的7个单元恰好符合Miller的结论。而较新的脑科学研究也显示, 人的信息处理局限于4个单元左右的信息[38]。因此, 三支决策采用三划分有其认知基础。
具体来讲, 三分是指基于特定的方法与目标将整体划分为3个互不相交的部分, 也称为3个域, 3个域合起来给出了整体的“三划分(tri-partition)”。根据各个问题的不同特点, 可以采用不同的三分法。这种对整体的三分也可以看作是从整体到局部, 从大粒度到小粒度, 从宏观到微观的转换。即, 将复杂问题转化为3个规模较小的问题。治略则是指根据三分的结果, 有针对性地设计策略和实施行动, 解决3个小问题, 从而提高决策质量, 减少决策成本, 降低决策时间, 以期达到某种收益的最大化或者代价的最小化。治略的前提是三分的结果必须有意义, 这样才有可能设计有效的措施和方法; 而治略则体现了三支决策中的“方法和策略”。图 1给出一个三分而治的三支决策模型[4]。
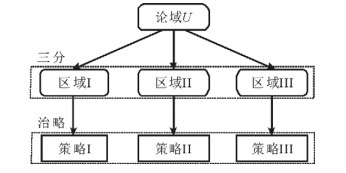
|
图 1 三分而治的三支决策模型 Fig. 1 Trisecting-and-acting model of threeway decisions |
三支决策的思想给出一个基于三元素的三角形研究方法。我们将一个研究领域或学科进行三划分, 把3个部分想象成一个三角形的3个顶点, 于是, 这三者之间的关系可以形成一个有机的系统“三点, 三线和一面”, 如图 2所示。在点层, 研究3个相互独立的点A, B和C。在线层, 研究两两相关的点组成的3条线AB, AC和BC。在面层, 研究3个相关点和三条线组成的一个三角形面ABC。这样, 三划分A, B, C给出了7个不同的侧重点或主题。由简到难, 由局部到整体, 由相对独立的点到相关联的线和面。
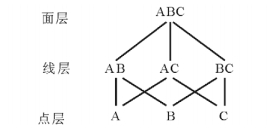
|
图 2 点-线-面的三层研究方法 Fig. 2 A three-level research method based on individual, pair, triplet analysis |
用三支决策的思想去研究和分析一种理论或者行为, 将会对我们起到指导作用。本文采用基于三支决策的研究方法, 将形式概念分析、粗糙集分析和粒计算这3种知识发现理论看作为一个三角形的3个顶点, 系统地探讨它们所用到的三支思想和方法, 以及3种理论的关系。
2 形式概念分析中的三支思想与方法 2.1 FCA三角形如前所述, FCA理论最基础的概念就是形式概念, 是对哲学中“概念”这一名词的形式化描述。因此, 一个形式概念的名称或者符号, 以及内涵与外延就形成了FCA理论中最基本的概念三角形, 而内涵与外延是建立在潜在的形式背景基础上的。这个关系反映在图 3中。
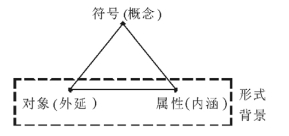
|
图 3 FCA中的概念三角形 Fig. 3 Concept triangle in FCA |
符号是这个概念的表达方式; 对象是概念反映的个体, 即外延; 而属性就是与对象相关的特征与描述, 即内涵。这种描述方式与Peirce符号论中的符号三角形相一致[39]。
2.2 FCA基本理论FCA的数据基础是一个形式背景(U, A, I), 其中, U是对象集, A是属性集, I是U与A之间的二元关系。
在对象子集X
| $ \begin{align} & {{X}^{*}}=\left\{ a|a\in A, \forall x\in X, xIa \right\}, \\ & {{B}^{*}}=\left\{ x|x\in U, \forall a\in B, xIa \right\}。\\ \end{align} $ |
X*表示X中所有对象共同具有的属性集合, B*表示共同具有B中所有属性的对象集合。
如果一个二元对(X, B)满足X*=B, 且B*=X, 则称(X, B)是一个形式概念, 简称概念。其中, X称为概念的外延, B称为概念的内涵。用L(U, A, I)表示形式背景(U, A, I)的全体概念,(X1, B1)和(X2, B2)是概念, 记(X1, B1)≤(X2, B2)
(X1, B1)∧(X2, B2)=(X1∩X2, (B1∪B2)**),
(X1, B1)∨(X2, B2)=((X1∪X2)**, B1∩B2)
也是概念, 从而L(U, A, I)是格, 并且是完备格。概念格可以用哈斯图直观刻画。
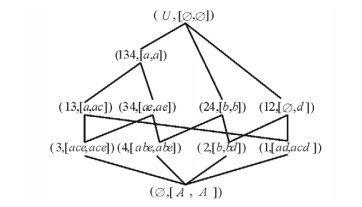
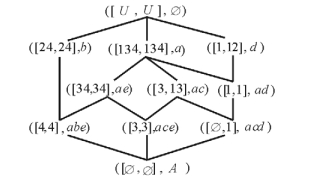
例1 表 1是一个形式背景(U, A, I), 其中, 对象集U={1, 2, 3, 4}, 属性集A={a, b, c, d, e}。如果对象与属性有关, 就在对象行与属性列的交叉处用1标记, 否则, 用0标记。其概念格如图 4所示。形式概念(24, abc)表示对象2与4共同具有的属性是a, b和c, 而共同具有这3个属性的对象也恰为2和4。
|
|
表 1 形式背景(U, A, I) Tab. 1 A formal context (U, A, I) |
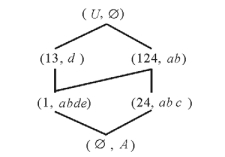
|
图 4 例1的概念格 Fig. 4 The concept lattice of Example 1 |
Wille在形式背景基础上给出的形式概念我们可以称之为经典概念, 因为这种概念最早、也最为纯粹的用形式化的方式反映了概念的哲学语义, 即内涵与外延的统一, 完美地以数学的形式表现出了哲学当中的概念。
但是, 尽管形式概念反映了内涵与外延之间的统一、彼此拥有的共存特点, 但是直观上还有一种信息没有反映出来, 即作为外延的对象集所共同不具有的属性。而这也是一种“共性”。
针对一个对象集X
三支概念分析的基本概念是三支概念以及三支概念格。按照从对象出发, 将属性集三分的理念, 可定义对象导出三支概念和对象导出三支概念格; 对偶地, 按照从属性出发, 将对象集三分的角度, 又可定义属性导出三支概念和属性导出三支概念格。
图 5是例1的对象导出三支概念格。下面以概念(13, (d, c))为例解释对象导出三支概念的语义。该概念表明:对象1与3共同具有的属性是d, 共同不具有的属性是c, 而共同具有d同时共同不具有c的对象也恰为1与3, 而{c}∪{d}的补集中的属性则是对象1与3具有差异的属性。所以, 该三支概念清晰、完整、准确地反映了一个对象子集的共性(包括正面的和负面的两种共性)与差异性。
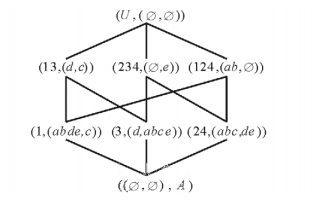
|
图 5 例1的对象导出三支概念格 Fig. 5 The object induced three-way concept lattice of Example 1 |
图 6是例1的属性导出三支概念格, 其中概念的解释与对象导出三支概念类似, 只不过是从属性角度出发, 考虑一个属性子集被对象集共同具有以及共同不具有的情况。
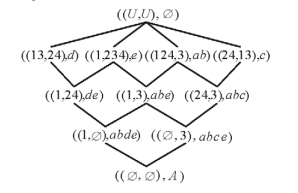
|
图 6 例1的属性导出三支概念格 Fig. 6 The attribute induced three-way concept lattice of Example 1 |
形式概念与三支概念都是在完备形式背景的基础上获取的, 但是我们更多面对的是信息不完整或者不明确的不完备形式背景。部分已知概念(partially-known FC)的提出很好地解决了这一类不完全数据的概念分析问题。
Burmeister和Holzer将不完备形式背景定义为一个四元组K=(U, A, {+, ?, -}, J), 其中J是一个三元关系J
(o, a, +)∈J:已知对象o具有属性a,
(o, a, -)∈J:已知对象o不具有属性a,
(o, a, ?)∈J:对象o是否具有属性a未知。
不完备背景把对象与属性之间的关系设置为3种:确切的具有, 确切的不具有, 以及未知。这种原始的三分关系很自然地将三支决策思想应用其中, 因而进一步分析时, 必将需要使用三支决策理论与思想。
不完备背景是完备背景的一种扩展, 完备背景则可以看作是特殊的不完备背景, 即, 不含有“?”的不完备背景。表 2是一个不完备背景的例子。
|
|
表 2 不完备背景(U, A, {+, ?, -}, J) Tab. 2 An incomplete formal context (U, A, {+, ?, -}, J) |
在不完备背景中, 无法用形式概念分析中的常规导出算子获得一个对象集共有的属性或者共有某些属性的对象集。根据三元关系的解释, Burmeister与Holzer将形式概念分析中常规的导出算子扩展为模态形式的导出算子[42], Yao在此基础上, 引入不完备背景的完备化思想, 利用区间集理论, 给出了部分已知概念的外延和内涵的区间-集合表示[43-44]。
假设概念的形式依然是二元对(外延, 内涵), 那么根据外延与内涵为经典集或者区间集可以得到四种不同的概念, 其关系如图 7所示。
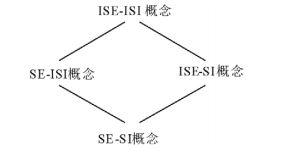
|
图 7 四种部分已知概念 Fig. 7 Four kinds of partially-known concepts |
SE-ISI概念最初由Li等提出[45], 其外延是经典集合, 而内涵是区间集, 它反映的信息是:从外延出发, 对概念涵盖的对象有精准的认知, 对内涵却只了解大概。而ISE-SI概念则与之相反, 强调的是从内涵的角度去认知, 对内涵的把握是准确的, 得到的外延只是大概的了解, 所以内涵是精确集而外延是区间集。最精确的概念莫过于SE-SI概念, 无论外延还是内涵, 都是精确的, 二者之间有强烈的依赖关系, 相互反映相关信息。形式概念就是SE-SI概念最好的例子。而最粗略的概念当属ISE-ISI概念, 无论外延还是内涵, 都是不够精确的, 需要用区间集来刻画。
例如, 图 8与图 9即分别是表 2所示不完备背景的SE-ISI概念形成的概念格以及ISE-SI概念形成的概念格。
3 粗糙集中的三支思想与方法
粗糙集理论的数据基础是信息系统。
定义1 称(U, A, F)为一个信息系统, 其中非空集合U={x1, x2, …, xn}为对象集, 每个xi(i≤n)称为一个对象; 非空集合A={a1, a2, …, am}为属性集, 每个aj(j≤m)称为一个属性; F={fj|fj: U→Vj, j≤m}为U和A的关系集, Vj为属性aj的值域。
RB={(xi, xj)|fl(xi)=fl(xj), ∀al∈B}是U上的一个等价关系, 从而产生U上的一个划分。
例2 表 3所示的信息系统中, 对象集U={x1, x2, x3, x4, x5}, 属性集A={a, b, c, d}。依据上述等价关系, U上的等价类有4个:{x1}, {x2, x5}, {x3}和{x4}。
|
|
表 3 信息系统(U, A, F) Tab. 3 An information system (U, A, F) |
针对一个数据集, 按照某种等价关系R建立的分类是粗糙集理论的研究基础。每个类, 以及可以表示为某些类的并的那些集合被认为是一个精确概念, 是可以被定义的。除此之外的集合都是不可被定义的。但是, 粗糙集理论可以给出这些不可定义的集合或者概念的一种近似表示。
粗糙集对不精确概念X的描述是通过其下近似R(X)和上近似R(X)这两个精确概念来实现的。一个概念的上近似由可能属于该概念的等价类组成, 其下近似由肯定属于该概念的等价类组成。所以, 上近似以外的部分(负域)一定与X全无交集, 而上下近似之间的部分(边界域)则是由那些其部分归于X、部分不归于X的等价类组成。
于是, 关于粗糙集理论的基本思想, 还有一种等价的理解方式。即, 粗糙集理论用正域(下近似)、负域和边界域三个两两互不相交的区域近似一个不可定义概念X。事实上, 这3个域恰好把整个论域分为了3个部分。而这又恰好对应了三支决策最基本的三分思想。因此, 粗糙集是三支决策理论的模型之一。
在粗糙集理论中, 概念的可定义性是基于描述实体的描述语言。对于正域中的实体, 我们可以通过它们的描述断定它们属于某个概念; 对于负域中的实体, 我们可以通过它们的描述断定它们肯定不属于某个概念; 而对于边界域中的实体, 对它们的描述则无法让我们断定它们一定属于或不属于这个概念。而事实上, 所谓正域, 就是X的下近似R(X), 即肯定属于概念X的那些等价类; 所谓负域, 就是所考虑对象的全体去除X的上近似后剩余的部分U-R(X), 也就是肯定不在概念X中的等价类; 而边界域就是X的上、下近似的差R(X)-R (X), 也就是可能属于概念X的等价类。
图 10给出了粗糙集理论中最基础的概念与思想的简单刻画。
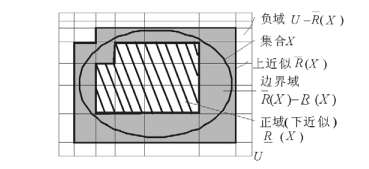
|
图 10 粗糙集基本概念图示 Fig. 10 Basic notions in theory of rough sets |
作为一个新的学科, 粒计算是基于多粒度的问题求解的理论、方法、技术和工具。自1997年Zadeh[28]首次提出了粒计算这一思想以来, 越来越多的学者将目光投向了粒计算的研究[30-32]。
粒计算是基于粒结构的计算。三元思维可以用来解释和描述粒结构, 即, 一个粒结构由粒、层和层次结构三大元素组成。基于三元思维, 可以将粒计算研究分为3个部分, 从哲学, 方法以及机制3个方面对粒计算进行刻画, 给出粒计算三元论[31, 35]。粒计算三元论对多种粒计算方法进行了合成, 形成了粒计算的一个统一框架。
粒计算三元论可以用一个三角形来描述, 如图 11所示。三角形的3个顶点分别表示粒计算哲学、方法和机制。每一个方面既影响着其他两个方面又被其他两个方面所影响, 故而并没有十分清晰的界限。3个部分交织在一起提供了一个完整的粒计算框架。
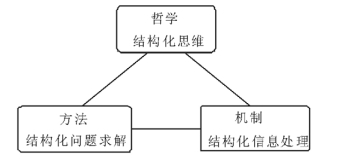
|
图 11 粒计算三角形 Fig. 11 Granular computing triangle |
一个粒可用3个元素共同刻画:粒的名称, 粒的描述以及粒中的实体。粒的描述就是粒的表示方式, 在我们的研究中可以是一个逻辑公式; 粒中的实体就是一族形成这个粒的对象; 粒的名称就是可以方便指代这个粒的一个标签。
定义2 称三元对(g, i(g), e(g))为一个粒, 其中g为粒的名称, i(g)为粒的一种描述, e(g)为粒中的实体的对象集。
该描述简洁的反映了由粒的三大要素所构成的粒三角形。值得注意的是, 在许多情形下, i(g)和g是相同的, 并不刻意加以区分。而此形式与FCA三角形(见图 3), 以及FCA中形式概念的描述本质上几乎是相同的。
粒计算是基于由不同粒所构成的粒结构的信息处理。粒结构的一个简单的例子就是划分。论域的划分实际上就是论域的一种分类, 每一个分好的块或者类代表一个概念的外延。这些块就可以当作同一层的粒来考虑。所以, 从划分的角度讲, 同一层的粒(块)是两两不相交的。
对同一个论域进行的不同划分之间可以定义粗细关系, 也就是不同划分的块之间的大小关系。利用这种关系可以建立一个论域的多层次粒结构。比如, 针对一个论域有两种粗细不同的划分, 就可以看作两个层次, 两种划分意味着可以从两个不同的层次水平分析数据。处于同一个层次内部的粒之间是两两不相交的, 分属于两个不同层次的粒之间或包含或不相交; 同层粒度对数据分析的作用是类似的, 不同层的粒度分析则起到互补的作用。因此, 形成了既有平面又有立体的信息分析网络, 其分析结果相互补充说明, 共同反映数据的更多信息。
5 形式概念分析与粗糙集 5.1 FCA与RS的联系FCA与RS是两种不同的数据分析方法, 它们从不同的侧面来研究和表现数据中隐含的知识。虽然是两种不同的理论, 但从原始数据、研究内容和研究目标, 以及方法论来说, 它们有许多相似之处。
如前文所述, FCA与RS的原始数据分别称为形式背景与信息系统, 其表达形式和所反映的信息类似。如果将信息系统的多值离散情况退化为布尔值, 就相当于一个形式背景; 而形式背景中关于对象与属性之间的关系若从简单的“具有”或者“不具有”扩展为具有信息的多个不同程度、层次, 则可以看作是信息系统。在这种情况下, 信息系统可以在FCA框架下称为多值形式背景, 而形式背景亦可在RS框架下称为二值信息系统。
RS的基础是等价关系(不可区分关系), 这种等价关系是由属性所决定的对象之间的二元关系, 它确定了对象集上的划分。FCA的基础是形式概念——由对象与属性之间的二元关系所确定, 以及形式概念之间的一种有序的层次结构——概念格。
事实上, Qi, Wei和Li已经给出了RS的基本粒(等价类)与FCA的基本粒(形式概念)之间的关系问题, 以及等价类与概念格之间的转换方法[46]。因此, 这两种理论在最基础的底层信息刻画上的关系已经明了, 这就意味着这两种理论后续的研究方法是可以互通的。
数据基础的相似性与基本粒的明晰关系使得FCA与RS的研究内容, 以及相关问题的研究思路与方法也有很高的相似性。比如, 二者在理论方面的研究均涉及相关数学性质、理论拓广、属性约简、附加决策的知识获取、规则提取, 以及与其他软计算理论的关系研究和互补研究等。
5.2 属性约简与属性三分属性约简是FCA与RS中比较基础的研究方向之一, 意图寻找较少的属性, 使其能体现原始数据所反映的某项知识, 最终达到降维的效果。比如, RS中经典的属性约简是在完备信息系统基础上寻求保持分类能力不变的极小属性集[47]。如例2信息系统的属性约简共有两个: {a, c}和{b, c}, 其中任何一个对于对象全体U的分类效果皆与利用原始属性集A进行分类的效果相同。FCA中的约简则是寻找保持概念格结构不变的极小属性集[22]。如例1形式背景的属性约简有两个:{a, c, d}和{b, c, d}, 其中任何一个与对象全集做成的子背景的概念格与原始数据的概念格是同构的。
除此之外, 两种理论也考虑了完备数据情形的其他约简, 比如RS中决策表不协调时的属性约简问题, FCA中保持粒概念外延不变的属性约简, 以及保持交(并)不可约元外延不变的属性约简。
RS与FCA中的属性约简问题都可以利用差别矩阵来求解, 但是差别矩阵的定义不同。RS中, 差别矩阵是从其基本粒——等价类的角度出发, 寻求任何两个等价类之间的差异来获取差别属性集以及相应的差别矩阵。FCA中, 差别矩阵是从其基本粒——形式概念的角度出发, 寻求任何两个形式概念之间的差异, 进而获取差别属性集以及相应的差别矩阵。
属性约简引发的一个非常自然的问题是:属性分类问题。因为有的属性被剔除, 有的则被保留。而被留下的这些属性其实也存在着重要性的差异。
RS的数据是以对象集、属性集、以及二者之间函数关系形成的信息系统为基础的, 而知识的分类主要是用属性来表达。事实上, 各个属性在表达知识分类中的作用是不同的。有些属性是绝对不必要的, 去掉这些属性, 并不会影响以分类为目的的知识发现过程与结果; 有些属性是绝对必要的, 去掉这些属性必然会影响到知识的发现; 而有些属性是相对必要的, 它必须与所有绝对必要属性搭配起来才不影响知识发现。因此, Wei等将信息系统中的属性自然而然分成三类[48], 即, 绝对不必要属性, 绝对必要属性, 也称核心属性, 以及相对必要属性。这就是属性的三分类问题。比如, 例2信息系统的4个属性中, c是核心属性, a与b是相对必要属性, d是绝对不必要属性。
FCA中亦是如此, 只不过FCA中我们更强调的是属性对于格结构的形成与维持所起的作用。比如, 例1形式背景中, c与d是核心属性, a与b是相对必要属性, e是绝对不必要属性。
通俗来讲, 属性根据所研究问题的性质可以被分为3类:核心属性, 相对有用属性, 无用属性。
6 形式概念分析, 粗糙集及粒计算将GrC的思想融入FCA与RS的研究是目前知识发现领域的一个重要研究方向。
一般来说, 一个具体模型中的粒是跟模型所描述的方式和所要研究的问题有关的。RS中的基本粒非等价类莫属。依据属性取值情况把对象分为一些等价类, 一个等价类刻画一类相同的事物, 这自然形成一个块。利用这个粒, 可以将任何一个集合的上下近似刻画出来, 从而对该集合有近似描述。前面第3节关于粗糙集的描述中, 可以把所有“等价类”都换成“粒”来理解和解释。
FCA中最基本的粒是形式概念; 从构造上来看, 对象概念与属性概念也是一种粒; 从格结构上看, 交、并不可约元也是一种粒。可见, FCA中基本的粒比较多, 这些多层次多视角的粒度, 形成一个网络, 从不同的层面反映形式背景及其概念格的信息。Qi等[49]从对象与属性两个不同角度对应给出五种粒, 有单一的对象/属性集, 也有(对象, 属性)二元对, 并层层递进, 引出普通形式概念和子格作为高层次的粒。这些粒从不同的角度和层次反映了FCA中有关导出算子、概念格结构等的信息。
从粒反映的信息来看, RS中的粒信息较为单调、简单, 因为仅用属性值做参考标准来考虑对象集的划分; 而FCA中的每一种不同粒都同时考虑属性与对象的对应关系, 更为详细深入。
7 结语3WD, GrC与FCA, RS是目前知识发现与不确定性分析领域中非常活跃的4个研究方向。3WD是一种广泛适用的研究思想与方法, 可以为很多具体的问题与模型提供研究框架。FCA与RS是两个具体的模型, 它们有各自的描述与解释, 涉及具体的研究内容。GrC则兼有思想与模型两个特点, 可以为人们提供一种很好的处理问题的研究方法, 也具有一些简单的模型; 但思想性不如3WD宏观与广泛, 模型不如FCA与RS具体。但是, 这些理论从不同的角度对我们所掌握的数据、所面对的世界进行描述、解释和分析, 得到很多不同的结论, 进一步指导我们的科研工作与生活。
这些理论所涉及的研究热点与分支很多, 绝不是这一篇文章可以解释清楚和完善的。我们仅在此文中尝试用三支决策的思想来解释另外3种理论, 剖析它们之间的联系。要想更为细致地分析透彻它们之间的关系, 还需要做很多更深入的工作。
| [1] |
YAO Y Y. An outline of a theory of three-way decisions [C]//YAO J T, YANG Y, SLOWINSKIN, et al (eds). Proceedings of 2012 Rough Sets and Current Trends in Computing (Lecture Notes in Computer Science, 7413), Chengdu, China, 2012: 1-17. https://www.researchgate.net/publication/268440623_An_Outline_of_a_Theory_of_Three-way_Decisions
|
| [2] |
姚一豫.三支决策研究的若干问题[M]//刘盾, 李天瑞, 苗夺谦, 等.三支决策与粒计算.北京: 科学出版社, 2013: 1-13.
|
| [3] |
姚一豫, 于洪.三支决策概述[M]//于洪, 王国胤, 李天瑞, 等.三支决策: 复杂问题求解方法与实践.北京: 科学出版社, 2015: 1-19.
|
| [4] |
YAO Y Y. Three-way decisions and cognitive computing[J]. Cognitive Computations, 2016, 8(4): 543-554. DOI:10.1007/s12559-016-9397-5 |
| [5] |
刘盾, 梁德翠. 广义三支决策与狭义三支决策[J]. 计算机科学与探索, 2017, 11(3): 502-510. |
| [6] |
于洪, 王国胤, 李天瑞, 等. 三支决策:复杂问题求解方法与实践[M]. 北京: 科学出版社, 2015.
|
| [7] |
刘盾, 李天瑞, 苗夺谦, 等. 三支决策与粒计算[M]. 北京: 科学出版社, 2013.
|
| [8] |
贾修一, 商琳, 周献中, 等. 三支决策理论与应用[M]. 南京: 南京大学出版社, 2012.
|
| [9] |
FUJITA H, LI T R, YAO Y Y. Advances in three-way decisions and granular computing[J]. Knowledge-Based Systems, 2016, 91: 1-3. DOI:10.1016/j.knosys.2015.10.026 |
| [10] |
XU W H, LI J H, SHAO M W, et al. Editorial[J]. International Journal of Machine Learning and Cybernetics, 2017, 8: 1-3. DOI:10.1007/s13042-016-0600-5 |
| [11] |
YAO J T, LI H X, PERTERS G. Decision-theoretic rough sets and beyond[J]. International Journal of Approximate Reasoning, 2014, 55: 99-100. DOI:10.1016/j.ijar.2013.09.022 |
| [12] |
PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Science, 1982, 11: 341-356. DOI:10.1007/BF01001956 |
| [13] |
PAWLAK Z. Rough sets:Theoretical Aspects of Reasoning about Data[M]. Boston: Kluwer Academic Publishers, 1991.
|
| [14] |
DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International Journal of General Systems, 1990, 17: 191-209. DOI:10.1080/03081079008935107 |
| [15] |
YAO Y Y. A comparative study of fuzzy sets and rough sets[J]. Information Sciences, 1998, 109: 227-242. DOI:10.1016/S0020-0255(98)10023-3 |
| [16] |
WU W Z, MI J S, ZHANG W X. Generalized fuzzy rough sets[J]. Information Sciences, 2003, 151(3): 263-282. |
| [17] |
MI J S, WU W Z, ZHANG W X. Approaches to knowledge reduction based on variable precision rough set model[J]. Information Sciences, 2004, 159(3-4): 255-272. DOI:10.1016/j.ins.2003.07.004 |
| [18] |
YAO Y Y. Three-way decisions with probabilistic rough sets[J]. Information Sciences, 2010, 180(3): 341-353. DOI:10.1016/j.ins.2009.09.021 |
| [19] |
WILLE R. Restructuring lattice theory: An approach based on hierarchies of concepts [C]//RIVAL I, ed. Ordered Sets. Reidel: Dordrecht-Boston, 1982: 445-470. http://www.springerlink.com/content/flwn006407565r6t
|
| [20] |
GANTER B, WILLE R. Formal Concept Analysis:Mathematical Foundations[M]. New York: Springer-Verlag, 1999.
|
| [21] |
YAO Y Y. Concept lattices in rough set theory [C]//DICK S, KURGAN L, PEDRYCZ W, et al.Proceedings of 2004 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS 2004). IEEE Catalog Number: 04TH8736, June 27-30, 2004, 796-801. http://www.researchgate.net/publication/4092886_Concept_lattices_in_rough_set_theory
|
| [22] |
张文修, 魏玲, 祁建军. 概念格的属性约简理论与方法[J]. 中国科学(信息科学), 2005, 35(6): 628-639. |
| [23] |
WILLE R. The basic theorem of triadic concept analysis[J]. Order, 1995, 12(2): 149-158. DOI:10.1007/BF01108624 |
| [24] |
LEHMANN F, WILLE R. A triadic approach to formal concept analysis [M]//ELLIS G, LEVINSON R, RICH W, et al. Conceptual Structures: Applications, Implementation and Theory (LNCS954). Heidelberg: Springer, 1995, 32-43.
|
| [25] |
BELOHLAVEK R, KLIR G J, WAY E C. Concepts and fuzzy sets:misunderstandings, misconceptions, and oversights[J]. International Journal of Approximate Reasoning, 2009, 51(1): 23-34. DOI:10.1016/j.ijar.2009.06.012 |
| [26] |
YAO Y Y. Rough-set concept analysis:interpreting RS-definable concepts based on ideas from formal concept analysis[J]. Information Sciences, 2016, 346-347: 442-462. DOI:10.1016/j.ins.2016.01.091 |
| [27] |
WU W Z, LEUNG Y, MI J S. Granular computing and knowledge reduction in formal contexts[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(10): 1461-1474. DOI:10.1109/TKDE.2008.223 |
| [28] |
ZADEH L A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy Sets and Systems, 1997, 90: 111-127. DOI:10.1016/S0165-0114(97)00077-8 |
| [29] |
LI J H, HUANG C C, QI J J, et al. Three-way cognitive concept learning via multi-granularity[J]. Information Sciences, 2017, 378(1): 244-263. |
| [30] |
PEDRYCZ W, SKOWRON A, KREINOVICH V. Handbook of granular computing[M]. John Wiley & Sons, West Sussex, 2008.
|
| [31] |
YAO Y Y. A unified framework of granular computing[M]. Handbook of Granular Computing, 2008: 401-401.
|
| [32] |
苗夺谦, 王国胤, 刘清, 等. 粒计算:过去、现在与展望[M]. 北京: 科学出版社, 2007.
|
| [33] |
WU W Z, LEUNG Y, MI J S. Granular computing and knowledge reduction in formal contexts[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(10): 1461-1474. DOI:10.1109/TKDE.2008.223 |
| [34] |
王国胤, 李德毅, 姚一豫, 等. 云模型与粒计算[M]. 北京: 科学出版社, 2012.
|
| [35] |
YAO Y Y. A triarchic theory of granular computing[J]. Granular Computing, 2016, 1(2): 145-157. DOI:10.1007/s41066-015-0011-0 |
| [36] |
WEI L, WAN Q. Granular transformation and irreducible element judgment based on pictorial diagrams[J]. IEEE Transactions on Cybernetics, 2016, 46(2): 380-387. DOI:10.1109/TCYB.2014.2371476 |
| [37] |
MILLER G A. The magical number seven, plus or minus two:some limits on our capacity for processing information[J]. Psychological Review, 1956, 63(2): 81-97. DOI:10.1037/h0043158 |
| [38] |
COWAN N. The magical number 4 in short-term memory:A reconsideration of mental storage capacity[J]. Behavioral and Brain Sciences, 2000, 24: 87-185. |
| [39] |
PEIRCE C S. Collected Papers[M]. Cambridge: Harvard University Press, 1931-1935.
|
| [40] |
QI J J, WEI L, YAO Y Y. Three-way formal concept analysis [M]//Miao D Q, Pedrycz W, Slezak D, et al(eds.). Rough Sets and Knowledge Technology (Lecture Notes in Computer Science, 8818), Shanghai, China, 2014: 732-741.
|
| [41] |
QI J J, QIAN T, WEI L. The connections between three-way and classical concept lattices[J]. Knowledge-Based Systems, 2016, 91: 143-151. DOI:10.1016/j.knosys.2015.08.006 |
| [42] |
BURMEISTER P, HOLZER R. On the treatment of incomplete knowledge in formal concept analysis [M]//GANTER B, MINEAU G W(eds). Proceedings of 2000 International Conference on Conceptual Structures (Lecture Notes in Computer Science, 1867), Darmstadt, Germany, 2000: 385-398.
|
| [43] |
YAO Y Y. Interval-set algebra for qualitative knowledge representation [C]//Proceedings of the 5th International Conference on Computing and Information, Sudbury, 1993: 370-374. http://dl.acm.org/citation.cfm?id=654597
|
| [44] |
YAO Y Y. Interval sets and three-way concept analysis in incomplete contexts[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 3-20. DOI:10.1007/s13042-016-0568-1 |
| [45] |
LI J H, MEI C L, LV Y J. Incomplete decision contexts:Approximate concept construction, rule acquisition and knowledge reduction[J]. International Journal of Approximate Reasoning, 2013, 54: 149-165. DOI:10.1016/j.ijar.2012.07.005 |
| [46] |
QI J J, WEI L, LI Z Z. A partitional view of concept lattice [M]//SLEZAK D, WANG G, SZCZUKA M, et al(eds). Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing (Lecture Notes in Computer Science, 3641), Regina, Canada, 2005: 74-83.
|
| [47] |
张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京: 清华大学出版社, 2005.
|
| [48] |
WEI L, LI H R, ZHANG W X. Knowledge reduction based on the equivalence relations defined on attribute set and its power set[J]. Information Sciences, 2007, 177: 3178-3185. DOI:10.1016/j.ins.2007.01.037 |
| [49] |
QI J J, WEI L, WAN Q. Multi-level granular view in formal concept analysis[J]. Granular Computing. Accepted. |
 2018, Vol. 48
2018, Vol. 48