仿射传播聚类算法(Affinity propagation clustering, APC)是Frey等人在science上提出的通过数据点之间相互传播消息来确定聚类的新方法[1-2],文献[3]公开了其源码。由于APC算法可以在短时间内获得更低的误差聚类结果、不依赖于初值的选取、不需要相似矩阵必须对称等优点, 已被广泛应用于众多领域, 例如文献[2]将其应用于图像处理、基因识别和路线规划; 文献[4]将其应用于文本聚类; 文献[5-7]将其应用于数据流分类; 文献[8]将其应用于室内定位中等。许多文献针对算法收敛速度和准确率方面, 在仿射传播算法应用中进行了改进研究。文献[9]通过数据的约束对等先验知识调整相似度矩阵来提高APC聚类算法的性能。文献[10]通过采用可变度量来改善相似性矩阵, 以此提高APC算法处理多种数据的能力。文献[11]将MapReduce与APC算法结合, 加速了APC算法的收敛速度。文献[12]将分层聚类的思想引入APC聚类的过程中, 提升了算法的准确性和收敛速度。文献[13]设计了一种新的聚类有效性指标来确定APC算法的最优聚类数。
这些研究的基础是建立在公开APC源码的基础上的,在公开源码中, 阻尼因子是APC算法的一个重要参数,算法的收敛问题主要通过调整阻尼因子的值解决。在公开源码中, 采用的是固定阻尼策略,若将阻尼因子设置成一个较小的值(0.5), 则有可能导致算法因发生震荡而难以收敛。因此, 通常通过将阻尼因子设置为一个较大的值(0.9)的策略来有效避免震荡, 但是这样会减慢算法的收敛速度。本文所提算法通过设置一个监视窗, 不断监视算法的震荡情况,根据算法的震荡情况自适应调整阻尼因子的值。当算法发生震荡时, 以一定的步幅不断增加阻尼因子的值以消除震荡;当算法不再震荡时, 就不再增加阻尼因子的值以保证算法的收敛速度。这种策略相比公开源码中的固定阻尼策略, 不仅可以有效避免震荡, 而且可以很大程度地保持阻尼因子较小时的收敛速度。试验数据来源于公开的UCI数据集[14], 代码在公开源码的基础上进行的修改, 因此可以再验证。通过多个UCI公开数据集试验证明了所提算法的有效性。
1 APC算法定义L维的数据集X={x1, x2, …, xM}, 其中M表示数据样本个数, xi={xi, 1, xi, 2, …, xi, L}(i∈{1, 2, …, M})表示数据的行向量。则任意两个参考点之间的相似度为
| $ \begin{array}{l} {\rm{sim}}\left( {i,j} \right) = - {\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|^2},\\ \forall i,j = \left\{ {1,2, \ldots ,M} \right\},i \ne j。\end{array} $ | (1) |
其中,用对角线上的数值sim(i, i)不使用式(1)计算。它的值用来表示参考度p, 其值越大,代表其成为聚类中心的可能性就越大。通常作法是将p取一个相同的固定值(一般取sim(i, i)的中值), 即将所有的数据成员都看作潜在的聚类中心。
APC算法的流程主要是传递吸引度(responsibility)和归属度(availability)两种类型的消息, 算法不断循环迭代更新这两种消息。定义R(i, j)为参考点i与候选聚类中心参考点j的吸引度, 反映了参考点j适合作为参考点i的聚类中心的程度。定义A(i, j)为参考点i与候选聚类中心参考点j的归属度, 反映了参考点i选择参考点j作为聚类中心的合适程度。A的初始值设为零,R的初始值设为sim(i, j)。R(i, j)通过式(2)和式(3)更新:
| $ \begin{array}{l} R\left( {i,j} \right) = {\rm{sim}}\left( {i,j} \right) - \mathop {\max }\limits_{j \ne j\prime } \{ A\left( {i,j\prime } \right) + \\ {\rm{sim}}\left( {i,j\prime } \right)\} , \end{array} $ | (2) |
| $ {R_ {\rm{iter}}} = (1 - {l_ {\rm{am}}}) \times {R_ {\rm{iter}}} + {l_ {\rm{am}}} \times {R_{{\rm{iter}} - 1}}。$ | (3) |
其中,Riter表示本次迭代中吸引度的值, Riter-1表示上一次迭代中吸引度的值。lam表示阻尼因子。
A(i, j)通过式(4)更新,
| $ \begin{array}{l} A\left( {i,j} \right) = \min\{ 0,R\left( {j,j} \right) + \\ \sum\limits_{i\prime \ne i,j} {\max\left\{ {0,R\left( {i\prime ,j} \right)} \right\}} \} , \end{array} $ | (4) |
| $ {A_ {\rm{iter}}} = (1 - {l_ {\rm{am}}}) \times {A_ {\rm{iter}}} + {l_ {\rm{am}}} \times {A_{{\rm{iter}} - 1}}。$ | (5) |
其中
| $ A\left( {j,j} \right) = \mathop {\max }\limits_{q\prime \ne k} \left\{ {0,R\left( {i\prime ,j} \right)} \right\}。$ | (6) |
R(i, j)和A(i, j)之和越大代表参考点j作为参考点i的聚类中心的可能性就越大。APC算法通过不断迭代更新R(i, j)和A(i, j)的值, 直到收敛产生若干个高质量的聚类中心, 同时产生了其类别下的类成员。
2 自适应阻尼因子的APC算法 2.1 问题描述APC算法的收敛特性是个开放性难题[15]。文献[2]通过在相似度加入少量的噪声和引入阻尼因子(lam)试图解决APC的震荡问题, 但文献[16]的研究表明,加入微小数量的噪音到相似度矩阵不是必须的, 因此,如何保证APC算法收敛主要依赖于lam的选择。lam的建议取值范围是[0.5, 0.9][2]。
APC算法是一个搜索能量函数最小值的方法。lam越小, APC算法的全局搜索能力就越强, 数据点之间的消息更新速度也就更快, 因此可以更快地找到能量函数最小值, 但可能会导致算法发生震荡, 拖慢收敛速度, 甚至使得算法难以收敛; 反之, lam取值越大, APC算法的局部搜索能力就越强, 可以很大可能地避免震荡, 但同时使得数据点之间的消息更新速度变慢而降低收敛速度。因此, 一个较好的方式就是在有效避免震荡的情况下, 取一个较小的阻尼因子的值, 才能保证算法有一个较好的收敛速度。
2.2 对发生震荡可能性的检测要有效避免震荡, 就需要提前检测到发生震荡的可能性, 并及时采取避免震荡的措施。因此,及时检测到发生震荡的可能性是非常重要的。文献[16]给出了APC算法发生震荡的公式, 但仍然指出APC算法的收敛问题是个开放性的难题, 因此很难去证明在什么条件下, APC算法一定收敛而不会发生震荡。尽管很难找到完全避免震荡的方法, 但通过检测发生震荡的可能性并预防震荡的方式,尽可能地避免震荡是可行的。为了描述震荡的特征并检测发生震荡的可能性, 本文提出了以下定义。
定义1 聚类数的增长方向:定义每次迭代中获取的聚类数的增长方向为dir,
| $ {\rm{dir}} = {K_ {\rm{iter}}} - {K_{{\rm{iter}} - 1}}。$ | (7) |
其中,Kiter和Kiter-1表示本次迭代和上一次迭代中获取到的聚类数。
定义2 震荡因子:当每次迭代中获取的聚类数的增长方向没有朝向目标聚类数时, 称之为出现了一次震荡因子。在APC算法中, 每次迭代中获取的聚类数应不断下降,最终收敛到一个稳定的聚类结果。因此,当dir>0时, 可以判定为出现了一次震荡因子,出现震荡因子说明算法有了发生震荡的可能性。
定义3 震荡因子数:给APC算法添加一个监视窗, 假定窗宽为W, 即每隔W次迭代进行一次监视行为。将一个监视窗中监视到震荡因子出现的次数c称之为震荡因子数。
震荡因子和震荡因子数可以用于检测和描述震荡的特征。震荡的可能方式可以分为以下3种:
1) 有限的震荡, 即震荡因子出现的次数是有限的, 表现为震荡因子数会最终趋向为0,并一直为0。例如在APC算法起初阶段, 都有可能发生有限的震荡。这种有限的震荡并不会造成算法的不收敛。
2) 周期性的震荡, 即震荡因子出现的次数呈现周期性, 表现为震荡因子数也呈现周期性。这种震荡会导致算法难以收敛。
3) 非周期性的无限震荡, 即震荡因子出现的次数不呈现周期性, 但会无限地出现。这种震荡也会导致算法难以收敛。
对3种震荡情况都要提前检测出发生震荡的可能性, 可以通过震荡因子数是否大于0来进行判断。因此本文采取的检测发生震荡的可能性的方式为判断震荡因子数是否大于0。当检测到发生震荡的可能性时, 通过自适应调整阻尼因子的值来避免震荡。
2.3 自适应阻尼因子根据前文的描述, 如何合理地自适应调整lam的值是本文论述的重点。lam值较小会导致震荡问题, 而lam较大会导致数据点间的消息速度更新过慢, 那么一个合理的方法就是, 根据震荡因子数来调节lam的值, 使得lam停留在一个使得震荡因子数为0的最小的lam值上。图 1给出了自适应阻尼因子的APC算法流程。
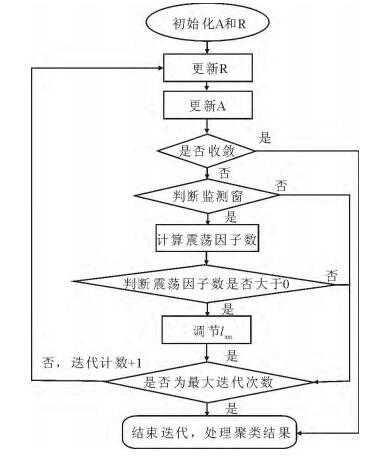
|
图 1 自适应阻尼因子的APC算法流程 Fig. 1 The APC algorithm flow with adaptive damping factor |
当在监视窗中检测到震荡因子数大于0时, 此时可以认为可能将要发生震荡, 因此需要调节lam的值。较为合理的方式就是采用震荡因子数来调节lam的值, 使得lam逐渐调节到震荡因子数为0为止。使用震荡因子数调节lam的方式为
| $ {l_ {\rm{am}}} = {l_ {\rm{am}}} + {\rm{step}}*c,{l_ {\rm{am}}} \in \left[ {0.5,0.9} \right]。$ | (8) |
其中,step是增长步幅, 本文设置为0.01。由式(8)可知, lam会根据震荡因子数的情况, 向lam的最大值0.9增长, 而当震荡因子数为0的时候, 就会停止增长。此时, APC算法将得到使得震荡因子数最小的lam值。而这个值, 可以有效避免震荡的同时, 保持较快的收敛速度。值得注意的是, 监视窗窗宽W的大小不宜取值过大或者过小, 过大会导致lam增长过慢, 而过小会导致lam增长过快, 推荐的取值范围为[5, 10]。
3 试验结果和分析 3.1 实验数据说明试验数据采用的是UCI的11个标准数据集[14], 表 1列出了数据集的相关信息。为了证明本文算法的有效性, 对不同的阻尼策略分别在收敛性、运行时间等方面进行了对比, 以证明本文阻尼策略的优势。
|
|
表 1 实验数据 Tab. 1 Experimental dataset |
表 2列出了算法运行的参数和运行环境。为了不让迭代次数影响算法, 设置最大迭代次数为100 000;噪声“noise”设置为“′nonoise′”, 即不加入噪声;其他参数值采用APC算法源码的默认参数。程序均运行在同一台台式电脑上。
|
|
表 2 算法运行的参数和运行环境 Tab. 2 The parameters and runtime environment of the algorithm |
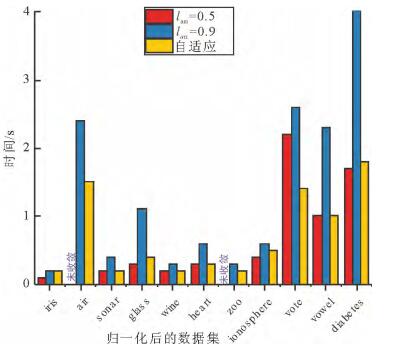
在本文选取的11个UCI数据集中, 采取未处理过的数据进行试验时, 并未发现APC算法因为震荡而不收敛的情况, 但是当将数据集进行归一化处理后, air和zoo数据集中出现了算法震荡且难以收敛。图 2和图 3分别是未归一化和归一化处理后的air数据集采用公开源码固定阻尼策略0.5和0.9,以及本文阻尼策略的聚类数变化结果。从图 2可知,lam越小,数据点之间的消息更新速度就越快,获取到的聚类数变化就越大,引起震荡的可能性就越大。lam越大,数据点之间的消息更新速度就越慢,获取到的聚类数变化相对较稳定,因此引起震荡的可能性就很低,但导致的问题是,由于数据点之间消息更新速度缓慢,因此需要更多的迭代次数才能收敛。图 3归一化的air数据集的聚类数变化结果中表明,阻尼因子0.5的情况就导致了算法的无限震荡而使得算法无法收敛。图 2和图 3都表明了本文的阻尼策略,起初阶段同阻尼因子0.5的情况,聚类数变化较快,但随着检测到震荡,通过增加阻尼因子的值,使得聚类数变化逐渐趋于平稳,最后当算法不再震荡时,则停止增长,保持当前收敛速度。图 4和图 5给出了所有数据集未归一化和归一化后的收敛情况和运行时间,表 3给出了具体的数据情况。从图 4可以看出,自适应阻尼策略保持了与固定阻尼值0.5差不多和大于固定阻尼值0.9的收敛速度。从图 5可以看出,阻尼值0.5引发了部分归一化后的数据集的震荡而使得算法难以收敛, 而自适应阻尼策略在可以避免震荡的同时, 还能保持较好的收敛速度。通过图 4和图 5的对比分析,进一步证明了本文阻尼策略的优势。
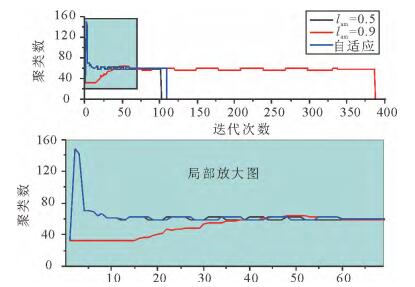
|
图 2 未归一化的air数据集的聚类数变化结果 Fig. 2 The changes of cluster number of no-normalized air dataset |
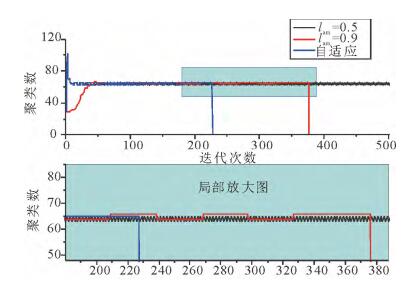
|
图 3 归一化的air数据集的聚类数变化结果 Fig. 3 The changes of cluster number of normalized air dataset |
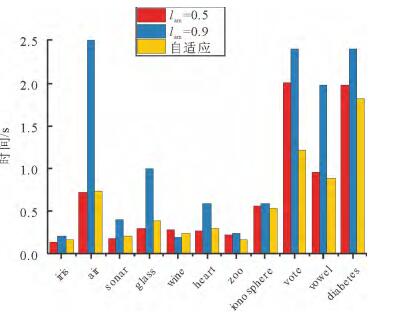
|
图 4 数据集未归一化的各类数据集运行时间对比 Fig. 4 Comparison of the running time of no-normalized dataset |
|
图 5 数据集归一化后的各数据集运行时间对比 Fig. 5 Comparison of the running time of the normalized dataset |
|
|
表 3 各数据集试验的具体数值 Tab. 3 Specific values for each dataset experiment |
本文提出了一种自适应阻尼因子的APC算法。通过设置一个监视窗不断监视算法的震荡情况,并统计监视窗内的震荡因子数, 通过震荡因子数调节阻尼因子的值来消除震荡。消除震荡后, 不再增加阻尼因子的值, 使得算法能保持一个较快的收敛速度。本文的阻尼策略不仅可以有效避免算法震荡而导致算法难以收敛, 而且可以保持一个较好的收敛速度。最后,通过多个UCI数据集进行试验, 证明了本文算法的有效性。
| [1] |
FREY B J, DUECK D. Response to comment on "clustering by passing messages between data points"[J]. Science, 2008, 319(5864): 726. |
| [2] |
FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972. DOI:10.1126/science.1136800 |
| [3] |
Frey Lab Probabilistic and Statistical Inference Group. Affinity Propagation (University of Toronto)[EB/OL]. [2017-03-10]. http://www.psi.toronto.edu/index.php?q=affinity%20propagation.
|
| [4] |
GUAN R, SHI X, MARCHESE M, et al. Text clustering with seeds affinity propagation[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(4): 627-637. DOI:10.1109/TKDE.2010.144 |
| [5] |
张建朋, 陈福才, 李邵梅, 等. 基于密度与近邻传播的数据流聚类算法[J]. 自动化学报, 2014, 40(2): 277-288. |
| [6] |
张震, 汪斌强, 李向涛, 等. 基于近邻传播学习的半监督流量分类方法[J]. 自动化学报, 2013, 39(7): 1100-1109. |
| [7] |
ZHANG X, FURTLEHNER C, GERMAIN-RENAUD C, et al. Data stream clustering with affinity propagation[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(7): 1644-1656. DOI:10.1109/TKDE.2013.146 |
| [8] |
FENG C, AU W S A, VALAEE S, et al. Received-signal-strength-based indoor positioning using compressive sensing[J]. IEEE Transactions on Mobile Computing, 2012, 11(12): 1983-1993. DOI:10.1109/TMC.2011.216 |
| [9] |
肖宇, 于剑. 基于近邻传播算法的半监督聚类[J]. 软件学报, 2008, 19(11): 2803-2813. |
| [10] |
董俊, 王锁萍, 熊范纶. 可变相似性度量的近邻传播聚类[J]. 电子与信息学报, 2010, 32(3): 509-514. |
| [11] |
鲁伟明, 杜晨阳, 魏宝刚, 等. 基于MapReduce的分布式近邻传播聚类算法[J]. 计算机研究与发展, 2012, 49(8): 1762-1772. |
| [12] |
张震, 汪斌强, 伊鹏, 等. 一种分层组合的半监督近邻传播聚类算法[J]. 电子与信息学报, 2013, 35(3): 645-651. |
| [13] |
周世兵, 徐振源, 唐旭清. 一种基于近邻传播算法的最佳聚类数确定方法[J]. 控制与决策, 2011, 26(8): 1147-1152. |
| [14] |
BLAKE C L, MERZ C J. UCI repository of machine learning databases (University of California)[EB/OL]. [2017-02-20]. http://archive.ics.uci.edu/ml/.
|
| [15] |
MÉZARD M. Where are the exemplars?[J]. Science, 2007, 315(5814): 949-951. DOI:10.1126/science.1139678 |
| [16] |
YU J, JIA C. Convergence analysis of affinity propagation[J]. Ksem, 2009, 5914: 54-65. |
 2018, Vol. 48
2018, Vol. 48