随着科技的发展, 具备拍照以及摄像功能的电子设备已大量进入人们的生活[1], 其呈现形式多种多样, 如智能手机、小型无人机、行车记录仪等。虽然这些电子设备给视频信息的采集提供了更多的方式,但是,由于手持设备的稳定性较差、小型无人机在空中的抖动及噪声的干扰, 视频图像的正常采集将受到影响, 视频画面会出现抖动、畸变等各种问题[2-4]。因此, 必须对摄像设备采集到的视频进行图像补偿处理[5], 以消除相机的非意向抖动(即外部噪声造成的被动抖动), 保留意向抖动(即摄像过程中的主动抖动), 从而改善视频的观察效果[6]。稳像技术按照作用机制通常分为3类:机械稳像[7]、光学稳像[8-9]以及电子稳像[10-11]。光学稳像通过光学部件自适应地调整光路补偿图像运动, 从而达到稳像效果。通过使用传统陀螺仪传感器等器件记录摄像平台的抖动情况, 机械稳像可对伺服系统进行逆向调整, 从而达到稳像效果。虽然以上两种稳像技术在图像补偿方面取得了很大的进展, 但因电子设备受到体积、成本、便携性等因素的限制, 光学稳像和机械稳像往往都不适合被应用到电子设备上。通过对连续视频序列之间的运动估计, 电子稳像可以对运动矢量进行滤波和运动补偿, 从而达到稳像效果[12]。
电子稳像技术主要分为2D和3D稳像技术[13]。2D稳像技术通过利用相邻图像帧之间的2D变换模型来达到稳像效果。虽然2D稳像技术计算较简单、算法较稳定, 但因其忽略了相机的3D运动信息, 无法取得较好的稳像效果。基于Lucas和Kanade[14]的思想, 卢晓燕等[15]提出了一种Harris结合光流的电子稳像算法。虽然这种2D稳像算法在车载抖动视频的处理上取得了较好的稳像效果, 但是Harris角点检测中的梯度运算过程较复杂, 而且当图像帧的特征不显著、特征点较少时, 就会造成很大的匹配误差。3D稳像技术通常利用3D运动模型, 并结合特征匹配或特征跟踪技术来获得好的稳像效果。基于图像渲染[16]的非度量稳像技术被认为是第一个3D稳像方案。Zhang等[17]提出的基于3D透视相机模型的稳像方案将稳像问题表示为平滑和相似约束下的二次成本函数。通过恢复原始3D运动和稀疏静态场景点云获得相机运动信息, 并保存形变技术修复图像的内容, Liu等[18]提出了基于保存内容的3D稳像方案。虽然以上这些算法在稳像方面取得了很大的进展, 但其3D重建计算过程比较复杂,因此, 一般用于实时性要求不高的情景中, 而且目前流行的智能电子设备计算能力较弱, 也不适用。
由于轻巧便携、成本低廉的特性, MEMS陀螺仪[19-20]方案在运动估计过程中更具备优势。MEMS陀螺仪可大大降低运动估计过程的计算量, 缩短系统运行时间。Karpenko等[21]提出了一种基于MEMS陀螺仪的电子稳像方法, 减少了稳像工作的计算量, 能解决视频的抖动问题。该方案虽然取得了好的稳像效果, 但其相机运动估计仅针对旋转运动, 忽略了平移运动。当相机距离拍摄物体较远时, 平移抖动相对于高频率的旋转抖动可以忽略不计, 但是, 目前的电子设备很多在室内使用, 当物体距相机较近时, 相机的平移抖动亦会严重影响拍摄效果。
针对文献[21]算法无法解决视频平移抖动的问题, 通过估计相机旋转抖动量[21]以及结合SIFT[22]方法估计图像在像素坐标系下的平移抖动量, 本文提出一种新的MEMS陀螺仪方法。该方法不仅增加了平移抖动量的估计, 而且还避免了特征匹配误差以及3D方法计算较复杂等问题。
1 MEMS陀螺仪相关介绍MEMS陀螺仪, 亦称作微机械陀螺仪, 其工作原理主要是利用科里奥利力。传统陀螺仪往往因为体积较大, 其应用范围受到很大影响。MEMS陀螺仪应运而生, 其小巧的特点完全符合便携电子设备的要求, 特别是可提高相机拍摄图像的稳定效果[23]。
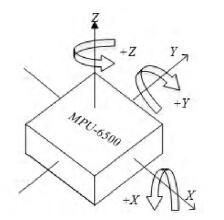
在电子稳像技术中, MEMS陀螺仪用于检测角速度(角速率), 也就是单位时间内的旋转角度, 单位为°/s。MEMS陀螺仪角速度的主要指标包括:量程、灵敏度、精度以及稳定性。以InvenSense公司的产品MPU-6500为例,对MEMS陀螺仪进行简单的介绍。如图 1所示, 该产品是六轴陀螺仪, 包括三轴角速度计和三轴角加速度计, 体积为3mm*3mm*0.9mm, 适用于大多数电子设备。
|
图 1 MPU-6500陀螺仪示意图 Fig. 1 Sketch map of MPU-6500 gyroscope |
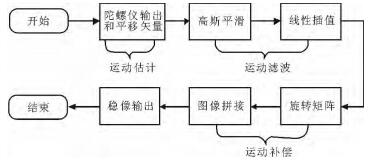
稳像技术包括3个阶段:运动估计、运动滤波以及运动补偿[24-25]。本文算法首先通过MEMS陀螺仪进行运动估计, 计算连续视频序列之间的旋转量。其次, 由于相机存在意向运动以及非意向运动, 利用高斯平滑滤波将摄像平台的非意向运动(高频率抖动)和意向运动(低频率抖动)进行分离, 得到精确的运动矢量。最后, 根据精确的相机运动矢量, 结合相机自身标定进行运动补偿, 得到稳定的视频序列, 算法流程如图 2所示。
|
图 2 算法流程图 Fig. 2 Flow chart of the algorithm |
首先, 采集连续的视频序列以及MEMS陀螺仪测量数据。利用MEMS陀螺仪的I2C接口获取陀螺仪数据(陀螺仪输出: 相机绕x, y, z这3个轴旋转的角速率)。其次, 根据陀螺仪采样数据的时间戳计算陀螺仪的采样频率。陀螺仪数据会受噪声的干扰, 因此必须有效地减少和抑制噪声以提高系统的精确性。最后, 对数据进行滤波处理, 将噪声和信号分离。意向运动通常是低频率的、比较平滑的, 消除高频率的非意向运动之后, 可获得比较平滑的数据。
视频图像在像素坐标系中的抖动(VPM)主要由相机旋转抖动(CRM)、相机平移抖动(CTM)和拍摄物体的运动(POM)3个因素造成, 可描述为
| $ {\rm{CRM}}+ {\rm{CTM}}+{\rm{POM}}\to {\rm{VPM}}。$ | (1) |
采用SIFT方法难免会有特征点落在运动物体上, 因为它们不属于相机运动, 必须将其剔除。
定义TOM为CTM和POM的组合, 可描述为
| $ {\rm{CTM}}+{\rm{POM}}={\rm{VPM}}- {\rm{CRM}}\to {\rm{TOM}}。$ | (2) |
利用拉依达准则[26]剔除落在运动物体上的特征点,其公式为
| $ |{f_i} - \mu | > 2s。$ | (3) |
其中,f是SIFT特征向量, μ是TOM的均值, s是TOM的标准方差。
剔除满足式(3)的特征点后, 式(2)变为
| $ {\rm{VPM}}- {\rm{CRM}}\to {\rm{CTM}}, $ | (4) |
即可获得平移抖动量。
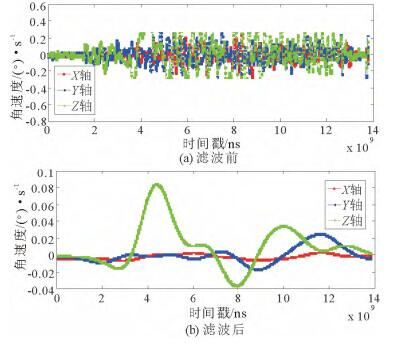
本文采用高斯平滑滤波[27]处理陀螺仪采样数据, 在Matlab平台上进行实验。图 3是陀螺仪数据滤波前后对比效果。高斯滤波器是一类根据高斯核函数的形状来选择权值的线性平滑滤波器, 高斯核函数为
|
图 3 陀螺仪数据滤波前后对比图 Fig. 3 The contrast of gyroscope data before and after filtering |
| $ k\left( {x - xc} \right) = {{\rm{e}}^{\frac{{ - {{\left( {x - xc} \right)}^2}}}{{2{\sigma ^2}}}}},x \in \left( { - \infty , + \infty } \right)。$ | (5) |
其中, xc表示核函数中心, σ表示核函数的宽度参数, 其值将直接影响平滑程度。
以高斯核函数为基础, 先生成给定大小的高斯核。然后, 将陀螺仪输出值与高斯核进行卷积并做差, 即可得到平滑的数据, 如式(6)所示。
| $ \left\{ \begin{array}{l} {\rm{gauss}}[] = {{\rm{e}}^{ - {x^2}/\sigma }},x \in \left( { - 120,120} \right)\\ {\rm{sum}}\_ {\rm{gauss}} = \sum\limits_{i = 1}^{240} {{\rm{gauss}}[i]} ,\\ {\rm{gauss}}\_ {\rm{kernal}}[\left] = {\rm{gauss}} \right[i]/{\rm{sum}}\_ {\rm{gauss}},\\ i \in \left( {1,240} \right)\\ {\rm{smooth}} = {\rm{gyroscope}} - {\rm{gyroscope}} \otimes {\rm{gauss}}\_ {\rm{kernal}}。\end{array} \right. $ | (6) |
相机平台的轻微抖动会造成图像在成像平面的旋转、平移。准确地说,抖动就是相机平台在三维世界中沿着3个坐标轴的旋转。在三维笛卡尔系坐标中, Pitch(俯仰角)表示绕x轴旋转, 会造成图像的垂直方向平移; Yaw(偏航角)表示绕z轴旋转, 会造成图像的水平方向的平移; Roll(翻滚角)表示绕y轴旋转, 会造成图像的旋转。处理三维旋转时, 通常采用旋转矩阵的方式描述。
获得相关陀螺仪数据之后,根据旋转角度=角速率*时间, 估计连续视频序列之间绕x轴, y轴和z轴旋转的角度ϕ, θ, ψ, 则旋转矩阵R(ϕ, θ, ψ)为
| $ \begin{array}{l} {\boldsymbol{R}}\left( {\phi ,\theta ,\psi } \right) = \\ (\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \phi }&{\sin \phi }\\ 0&{ - \sin \phi }&{\cos \phi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \theta }&0&{ - \sin \theta }\\ 0&1&0\\ {\sin \theta }&0&{\cos \theta } \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{\sin \psi }&0\\ { - \sin \psi }&{\cos \psi }&0\\ 0&0&1 \end{array}} \right]。\end{array} $ | (7) |
由于陀螺仪的采样频率(微秒级)和连续视频序列间的帧间隔(毫秒级)的不一致性, 某一时刻的视频图像帧可能无对应的陀螺仪数据。为了提高算法的精确度, 获得更好的稳像效果, 需要采用插值技术, 估计出连续视频序列间的旋转角度。根据陀螺仪的采样频率和连续视频序列,分别对ϕ, θ, ψ进行线性插值, 即可得连续视频序列之间的旋转角度Δϕ, Δθ, Δψ, 对应的旋转矩阵为R(Δϕ, Δθ, Δψ)。
2.3 运动补偿得到连续视频序列对应点之间的旋转角度之后, 通过逆向补偿的方式即可得到稳定的连续视频序列。
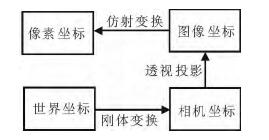
2.3.1 相机标定真实世界中物体是处于一个三维坐标系中, 而相机采集得到的图像是处于一个二维坐标系中, 相机标定[28]是二维图像和三维世界间的重要纽带, 关联到4个坐标系。世界坐标系, 用于描述三维空间中的物体、相机的坐标位置; 摄像机坐标系, 原点为相机光心的三维坐标系; 图像坐标系, 原点为像平面与光轴交点的直角坐标系(单位:mm); 像素坐标系, 原点为图像左上角点的直角坐标系(单位:像素), 像素坐标系的u轴和v轴与图像坐标系的x轴和y轴平行, 像素点在图像中的列数和行数分别用u和v表示。利用这4个坐标系, 相机成像过程可表示为如图 4所示的过程。
|
图 4 相机成像过程 Fig. 4 Camera imaging process |
1) 世界坐标系——相机坐标系
将相机看作是世界坐标系中某点, 可通过旋转矩阵(R)和平移矩阵(T)来描述,
| $ \left[ \begin{array}{l} {X}_ {\rm{c}}\\ Y_ {\rm{c}}\\ Z_ {\rm{c}}\\ 1 \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}_{3 \times 3}}}&{{{\boldsymbol{T}}_{3 \times 1}}}\\ {\boldsymbol{O}}&1 \end{array}} \right]\left[ \begin{array}{l} {X_ {\rm{w}}}\\ Y_ {\rm{w}}\\ Z_ {\rm{w}}\\ 1 \end{array} \right]。$ | (8) |
其中, 带下标w的参数表示世界坐标系中的点, 带下标c的参数表示相机坐标系中的点, R和T则分别表示旋转矩阵和平移矩阵。在这里, 假定相机坐标系原点与世界坐标系原点重合。
2) 相机坐标系——图像坐标系
实现三维空间中的点到二维图像平面点的变换。根据三角形相似原理, 图像坐标系中的点与相机坐标系中的点关系描述为p,
| $ {\boldsymbol{p}} = \left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right], $ |
| $ {Z_ {\rm{c}}}\left[ \begin{array}{l} x\\ y\\ 1 \end{array} \right] = \left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} X_{\rm{c}}\\ {{Y_{\rm{c}}}}\\ {{Z_{\rm{c}}}}\\ 1 \end{array}} \right], $ |
| $ \left\{ \begin{array}{l} x = \frac{{fX_ {\rm{c}}}}{Z_ {\rm{c}}},\\ y = \frac{{fY_ {\rm{c}}}}{Z_ {\rm{c}}}。\end{array} \right. $ | (9) |
其中,f为相机焦距。
3) 图像坐标系——像素坐标系
假设(u0, v0)表示相机的轴心坐标, 图像上的像素点坐标(u, v)分别表示每一帧采集的图像在系统中存储的数组的列数与行数, 则坐标(u, v)所对应的值就是该点的灰度值。dx表示每个像素沿x轴的实际物理尺寸大小, dy表示沿y轴的实际物理尺寸大小, 单位为mm。图像坐标系中的点与像素坐标系中的点关系描述为k,
| $ {\boldsymbol{k}} = \left[ {\begin{array}{*{20}{c}} {1/{d_x}}&\lambda &{{u_0}}\\ 0&{1/{d_y}}&{{v_0}}\\ 0&0&1 \end{array}} \right], $ |
| $ \left[ \begin{array}{l} u\\ v\\ 1 \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {1/{d_x}}&\lambda &{{u_0}}\\ 0&{1/{d_y}}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ \begin{array}{l} x\\ y\\ 1 \end{array} \right], $ |
| $ \left\{ \begin{array}{l} u = \frac{x}{{{d_x}}} + {u_0},\\ v = \frac{y}{{{d_y}}} + {v_0}。\end{array} \right. $ | (10) |
其中,λ表示扭曲因子,一般为0。
2.3.2 相邻图像补偿假设真实场景中的一点x, 在连续视频序列的第i帧(假设该视频帧为陀螺仪在t-1时刻的采样)的投影点为xi(像素坐标系), 在连续视频序列的第j帧(假设该视频帧为陀螺仪在t时刻的采样)的投影点为xj(像素坐标系)。
当相机没有旋转, 并且忽略平移运动时,
| $ \begin{array}{l} {x_i} = {\boldsymbol{kpR}}{X_ {\rm{w}}} = {\boldsymbol{KR}}{X_{\rm{w}}},\\ {x_j} = {\boldsymbol{kpR}}{X_{\rm{w}}} = {\boldsymbol{KR}}{X_{\rm{w}}}。\end{array} $ | (11) |
其中, k和p表示仿射变换矩阵和透视投影矩阵, K=k*p表示内参数矩阵, R表示刚体变换, Xw表示世界坐标系中的点坐标。
当相机出现旋转运动时,
| $ \begin{array}{l} {x_j} = {\boldsymbol{KR}}(\Delta \phi ,\Delta \theta ,\Delta \psi ){\boldsymbol{R}}{X_{\rm{w}}} = \\ {\boldsymbol{KR}}(\Delta \phi ,\Delta \theta ,\Delta \psi ){\boldsymbol{R}}{\left( {{\boldsymbol{KR}}} \right)^{ - 1}}{x_i} = \\ {\boldsymbol{KR}}(\Delta \phi ,\Delta \theta ,\Delta \psi ){{\boldsymbol{K}}^{ - 1}}{x_i}。\end{array} $ | (12) |
式(12)表明, 该过程是相机旋转时像素坐标的变化过程。欲实现稳像, 只需对当前的视频帧进行反向旋转和反向平移即可得到之前的抖动点坐标,
| $ \begin{array}{l} {x_{{j\_ }{\rm{new}}}} = {(KR(\Delta \phi ,\Delta \theta ,\Delta \psi ){{\boldsymbol{K}}^{ - 1}})^{ - 1}}{x_j} - {\rm{CTM}} = \\ {\boldsymbol{KR}}^{ - 1}(\Delta \phi ,\Delta \theta ,\Delta \psi ){{\boldsymbol{K}}^{ - 1}}{x_j} - {\rm{CTM}}。\end{array} $ | (13) |
连续的视频序列经过运动补偿之后, 能够得到稳定的图像效果。但由于图像的旋转、平移补偿, 有些图像的边缘部分可能会移出成像平面, 造成图像信息的丢失, 成像平面的边缘出现黑色区域, 影响视频的视觉效果。因此, 为了获得更佳的视觉效果, 必须通过一定的处理, 将稳定的视频图像更好地显示出来。目前比较常用的方法是对视频图像黑边进行一定比例的裁剪, 然后再显示稳定的图像。这种方法简便、处理速度较快,但是,也存在一定的弊端, 如造成图像边缘信息的丢失、图像分辨率降低, 影响图像视觉效果,对于抖动幅度较大的图像序列, 亦可能存在黑边处理不彻底的现象。
为解决裁剪方法的弊端, 文献[22]提出采用图像拼接补偿图像的黑边, 取得了较好的填充效果, 但拼接边界依然存在较明显的拼接痕迹。本文在此基础上, 采用加权融合的策略进行拼接, 以更好地保证边界平滑、无明显拼接痕迹。
对图像重叠区域的灰度值进行加权求和处理, 加权求和后的灰度值为
| $ \begin{array}{l} f\left( {x,y} \right) = {w_1}\left( {x,y} \right){f_1}\left( {x,y} \right) + \\ {w_2}\left( {x,y} \right){f_2}\left( {x,y} \right)。\end{array} $ | (14) |
其中, w1,w2为权值, 其和为1, x,y为重叠区域像素点的横纵坐标。权值的渐变过程为
| $ \begin{array}{l} {w_1} = \frac{{{x_r} - {x_i}}}{{{x_r} - {x_l}}},\\ {w_2} = 1 - {w_1} = \frac{{{x_i} - {x_l}}}{{{x_r} - {x_l}}}。\end{array} $ | (15) |
其中, xi为当前像素点横坐标, xl,xr为重叠区域左右边界坐标, w1由1逐渐变为0, w2由0逐渐变为1。
3 实验结果实验采用Visual Studio和Matlab联合编程, 实验处理及分析在HP Pro Desk 680 G1 TWR平台上进行, 内存为8G, CPU为3.6GHz。本文采用文献[29]提供的CMOS[30]传感器相机拍摄测试视频, 图像原始分辨率为1280*720。随机抽取视频序列1的第39帧和第123帧图像, 图 5为经过运动补偿和黑边补偿的结果。

|
图 5 本文方法实验结果 Fig. 5 The experimental results of this method |
图 6为相邻帧图像稳像前后的差值分析图, 其中, 第一行为当前帧图像稳像前与参考帧的差值图像; 第二行为当前帧图像稳定后与参考帧的差值图像。从图 6中可以看出,原图像序列在经过稳像处理后, 平滑效果得到了改善。

|
图 6 稳像前后差值分析图 Fig. 6 Difference analysis diagram before and after image stabilization |
为了更好地说明本文算法对视频序列处理的稳定性, 本文针对视频序列1和视频序列2, 分别就算法效率和精确性与文献[17]、文献[18]、文献[21]的算法进行对比分析。
算法效率:以每帧图像的处理时间为标准, 对比结果如表 1所示。实验结果表明, 相比恢复相机本身的3D空间运动信息, 本文算法大大降低了运动估计过程的计算量, 算法效率更提高。对视频序列1, 每帧图像平均处理时间比文献[18]算法减少了56.72%, 比文献[17]算法减少了59.93%。对视频序列2, 比文献[18]算法减少了56.62%, 比文献[17]算法减少了59.69%。由于本文算法增加了平移抖动量的估计, 因此比文献[21]算法运行时间有所增加。
|
|
表 1 不同算法效率比较 Tab. 1 Effciecy comparison of different algorithms |
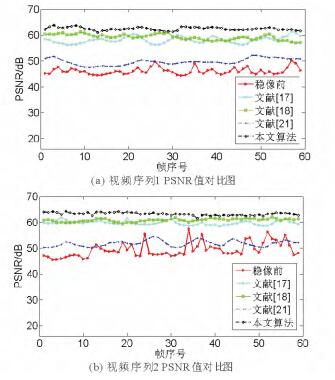
算法精确性:以峰值信噪比PSNR作为算法精确性的评价指标,信噪比越大表明算法的稳像效果越好[31],帧间平均PSNR值对比结果如表 2所示。图 7和图 8分别是各算法对视频序列1的第39帧图像和视频序列2的第46帧图像进行稳像处理的效果对比图。以视频序列1的前60帧为例,视频序列稳像前后的PSNR值对比如图 9(a)所示;以视频序列2的前60帧为例,视频序列稳像前后PSNR值对比如图 9(b)所示。实验结果表明,对于视频序列的稳像处理,相比其他算法,本文提出的算法稳定性更好,精确性更高。对视频序列1,使用本文算法得到的PSNR值比文献[17]算法提高了7.5%,比文献[18]算法提高了5.45%,比文献[21]算法提高了25.60%。对视频序列2,使用本文算法得到的PSNR值比文献[17]算法提高了5.87%,比文献[18]算法提高了4.03%,比文献[21]算法提高了22.11%。
|
|
表 2 不同算法精确性比较 Tab. 2 Accuracy comparison of different algorithms |

|
图 7 不同算法对视频序列1稳像效果图 Fig. 7 Image stabilization of video sequence 1 by different algorithms |

|
图 8 视频序列2稳像效果图 Fig. 8 Image stabilization of video sequence 2 by different algorithms |
|
图 9 稳像前后不同算法精确度对比图 Fig. 9 Accuracy contrast diagram of different algorithms before and after image stabilization |
通过陀螺仪估计相机的旋转抖动量, 再结合SIFT方法估计相机的平移抖动量, 本文提出的基于MEMS陀螺仪的电子稳像算法取得了较好的稳像效果, 而且避免了特征匹配计算复杂、匹配误差等问题。实验结果表明, 利用陀螺仪进行相机运动估计是准确的, 对于抖动视频具有较好的补偿效果, 视频质量大幅提升。而且算法计算量大大降低, 处理速度得到提高。本文算法具有较强的稳定性、准确性。
| [1] |
BATTIATO S, GALLO G, PUGLISI G, et al. SIFT features tracking for video stabilization[C]//International Conference on Image Analysis and Processing. Modena: IEEE Computer Society, 2007: 825-830. https://dl.acm.org/citation.cfm?id=1305091
|
| [2] |
韩绍坤, 赵跃进, 刘明奇. 电子稳像技术及其发展[J]. 光学技术, 2001, 27(1): 71-73. |
| [3] |
OVREN H, FORSSEN P E. Gyroscope-based video stabilization with auto-calibration[C]//IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015: 2090-2097. 10.1109/ICRA.2015.7139474
|
| [4] |
FORSSEN P E, RINGABY E. Rectifying rolling shutter video from hand-held devices[C]//The IEEE Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 507-514. https://csdl.computer.org/csdl/proceedings/cvpr/2010/6984/00/05540173-abs.html
|
| [5] |
李计添, 何永强, 陈财森, 等. 一种基于灰度投影算法的车载电子稳像算法[J]. 红外技术, 2010, 32(6): 328-332. |
| [6] |
RAWAT P, SINGHAI J. Review of motion estimation and video stabilization techniques for hand held mobile video[J]. Signal and Image Processing:An International Journal (SIPIJ), 2011, 2(2): 159-168. DOI:10.5121/sipij |
| [7] |
YU Q, WU B, JIAO Y, et al. Summarization of electronic image stabilization[C]//International Conference on Computer-Aided Industrial Design and Conceptual Design (CAIDCD). IEEE, 2006: 1-5. https://ieeexplore.ieee.org/document/4127038/
|
| [8] |
SATO K, ISHIZUKA S, NIKAMI A, et al. Control techniques for optical image stabilizing system[J]. IEEE Transactions on Consumer Electronics, 1993, 39(3): 461-466. DOI:10.1109/30.234621 |
| [9] |
谷素梅, 曲鲁杰. 小型光惯稳跟仪器稳像精度测试方案探讨[J]. 光学技术, 1993(2): 26-27. |
| [10] |
ZHANG Y X, ZHANG W G, ZHAO X X, et al. Study on electronic image stabilization system based on MEMS gyro[C]//International Conference on Electronic Computer Technology. IEEE Computer Society, 2009: 641-643. https://ieeexplore.ieee.org/document/4796042/
|
| [11] |
王志民, 徐晓刚. 电子稳像技术综述[J]. 中国图象图形学报, 2010, 15(3): 470-480. DOI:10.11834/jig.20100318 |
| [12] |
范永杰, 陈华. 基于MEMS陀螺仪的实时电子稳像技术[J]. 红外技术, 2015, 37(9): 724-727. |
| [13] |
JIA C, EVANS B L. Online calibration and synchronization of cellphone camera and gyroscope[C]//Global Conference on Signal and Information Processing. Texas: IEEE, 2013: 731-734. https://ieeexplore.ieee.org/document/6736995/
|
| [14] |
LUCAS B D, KANADE T. An iterative image registration technique with an application to stereo vision[C]//International Joint Conference on Artificial Intelligence. San Francisco: Morgan Kaufmann Publishers, 1981: 674-679. https://dl.acm.org/citation.cfm?id=1623280
|
| [15] |
卢晓艳. 电子稳像技术研究[D]. 西安: 西安工业大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10702-1013174445.htm
|
| [16] |
BUEHLER C, BOSSE M, MCMILLAN L. Non-metric image-based rendering for video stabilization[C]//Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE, 2003: 609. https://ieeexplore.ieee.org/document/991019/
|
| [17] |
ZHANG G, HUA W, QIN X, et al. Video stabilization based on a 3D perspective camera model[J]. Visual Computer, 2009, 25(11): 997-1008. DOI:10.1007/s00371-009-0310-z |
| [18] |
LIU F, GLEICHER M, JIN H, et al. Content-preserving warps for 3D video stabilization[J]. ACM Transactions on Graphics, 2009, 28(3): 1-9. |
| [19] |
李冰, 张超. 传感器电子稳像的块匹配提前中止方法[J]. 光电工程, 2016, 43(11): 76-81. DOI:10.3969/j.issn.1003-501X.2016.11.012 |
| [20] |
HANNING G, FORSLOW N, FORSSEN P E, et al. Stabilizing cell phone video using inertial measurement sensors[C]//IEEE International Conference on Computer Vision Workshops. IEEE, 2012: 1-8. https://ieeexplore.ieee.org/document/6130215/
|
| [21] |
KARPENKO A, JACOBS D, BAEK J, et al. Digital video stabilization and rolling shutter correction using gyroscopes[R]. Palo Alto: Stanford Tech Report CTSR, 2011. https://www.mendeley.com/research-papers/digital-video-stabilization-rolling-shutter-correction-using-gyroscopes/
|
| [22] |
HU R, SHI R, SHEN I, et al. Video stabilization using scale-invariant features [C]//International Conference on Information Visualization. IEEE, 2007: 871-877. https://dl.acm.org/citation.cfm?id=1271604
|
| [23] |
ESFANDYARIJ, NUCCIOR D, GANGX. MEMS陀螺仪技术简介[J]. 电子与电脑, 2011(4): 23-26. |
| [24] |
MATSUSHITA Y, OFEK E, GE W, et al. Full-frame video stabilization with motion inpainting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(7): 1150-1163. DOI:10.1109/TPAMI.2006.141 |
| [25] |
郑鸿云, 赵红颖, 魏云鹏, 等. 小型无人机快速最优化稳像方法研究[J]. 影像科学与光化学, 2016, 34(1): 51-58. DOI:10.7517/j.issn.1674-0475.2016.01.051 |
| [26] |
林洪桦. 测量误差与不确定度评估[M]. 北京: 机械工业出版社, 2009: 312-322.
|
| [27] |
LIU F, GLEICHER M, WANG J, et al. Subspace video stabilization[J]. ACM Transactions on Graphics, 2011, 30(1): 623-636. |
| [28] |
ZHANG Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 |
| [29] |
BELL S, TROCCOLI A, PULLI K. A non-linear filter for gyroscope-based video stabilization[C]//Proceedings of the 13th European Conference on Computer Vision. New York: Springer, 2014: 294-308. https://link.springer.com/chapter/10.1007%2F978-3-319-10593-2_20
|
| [30] |
EIGAMAL A, ELTOUKHY H. CMOS image sensors[J]. Circuits and Devices Magazine IEEE, 2005, 21(3): 6-20. DOI:10.1109/MCD.2005.1438751 |
| [31] |
陈滨, 赵建军, 杨利斌. 视频稳像评价方法研究[J]. 科学技术与工程, 2016, 16(22): 219-224. DOI:10.3969/j.issn.1671-1815.2016.22.039 |
 2018, Vol. 48
2018, Vol. 48