钢轨波浪形磨耗(简称波磨)是钢轨投入使用后, 由于轮轨接触而在轨顶面产生的沿纵向分布的周期性类似波浪形状的不平顺现象, 是轨道损伤的主要形式。它不但危及行车安全, 还产生大量的噪音, 甚至导致列车脱轨[1]。因此, 快速有效的测量和周期性的维护对减缓轨道波磨是非常必要的。
轨道波磨是空间分布的随机变形, 波长范围从几十毫米到百余米, 波长越长幅值越大, 要将其完全准确地检测出来是很困难的[2-5]。由于车辆动力学性能不同, 不同速度的车辆只对一定波长范围的轨道波磨有响应:在高速条件下, 20~70m的波磨, 将使固有频率较低的车体发生激振; 一般铁路或重载铁路(速度80~120km/h)只对中波长(5~12m)波磨加以限制; 高速铁路或动车组特别重视对短波长(30~1 000mm)波磨的控制, 避免形成共振[6-7]。因此, 通常设置波磨检测的全波段为30mm~60m。
现有的轨道波磨测量方法可以归纳为惯性基准法和弦测法两种。惯性基准法通过转向架轴箱加速度的二次积分来表征波磨值, 能比较如实地反映0.1~50m波长范围内的轨道不平顺[8-10]。其缺点是由于高通滤波器的影响, 在10km/h以下低速测量长的不平顺时误差较大, 遇台阶形不平顺时, 基线产生局部扭曲, 一般仅应用于大型的轨道检测车上[11-12]。弦测法是测量轨道波磨的另一种常用方法, 它以首尾两端的连线作为弦, 中间的测点到弦的距离作为波磨测量值[13-14]。针对系统传递函数不恒等于1的缺陷, 它通过逆滤波对弦测值进行二次处理, 使得复原波形逼近轨道真实状态[15-17]。和惯性基准法相比, 弦测法最大的优势是测量值不受行车速度的影响, 本文采用弦测法来构建钢轨波磨测量系统。
使用逆滤波对弦测数据进行复原时, 由于传递函数的制约, 每种弦测方法都只能对某一波长范围的轨道波磨进行有效检测, 无法同时覆盖30mm~60m全部检测波段。另外, 传统的逆滤波器采用频率采样法进行设计, 需要同时计算传递函数在对称区间每一个采样点上的幅频和相频特性[18-20]。而短波检测特性较好的偏弦法[21]传递函数比较复杂, 相频特性推导难度较大, 这也限制了弦测法在轨道波磨检测中的推广应用。
为此, 本文通过分析两点弦和三点偏弦传递函数的幅频特性, 首次提出一种基于两种方法相结合的钢轨波磨广域测量方法。该方法一方面使用最小二乘法来设计逆滤波器, 不仅只用计算半对称区间上传递函数的幅频特性, 而且较传统的频率采样法省去了相频特性的计算, 简化了设计难度; 另一方面在三点偏弦法的架构下, 通过3个检测点的灵活组合, 将两点弦的长波测量与三点偏弦的短波测量优势进行互补, 实现了单个系统下的30mm~60m全波段弦测波形的准确复原与测量。针对我国铁路线上主要使用的60kg/m钢轨进行的钢轨波磨测量实验表明, 本文方法能在不增加测量成本的条件下较为精确地对广域轨道波磨进行测量, 具有一定的理论及工程应用价值。
1 弦测法的基本原理 1.1 两点弦测法两点弦测法(Two-point verse sine method, 2VSM)检测点位置分布及原理如图 1所示。
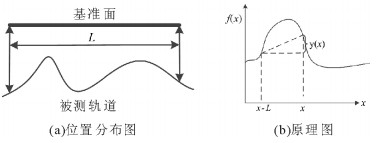
|
图 1 两点弦测法示意图 Fig. 1 The schematic diagram of 2VSM |
设轨道的实际不平顺值为f(x), 系统测量的弦测值为y(x), 则
| $ y\left( x \right) = f\left( x \right) - f\left( {x - L} \right), $ | (1) |
转换到频域, 则
| $ \begin{array}{l} Y\left( \omega \right) = F\left( \omega \right) - F\left( \omega \right){{\rm{e}}^{ - {\rm{j}}\omega L}} = \\ F\left( \omega \right)\left( {1 - {{\rm{e}}^{ - {\rm{j}}\omega L}}} \right) = F\left( \omega \right)H\left( \omega \right) \end{array} $ | (2) |
其中,λ为波长,L为弦长,H(ω)为频域传递函数, H(ω)=1-e-jωL,ω为角频率, ω=2π/λ。
1.2 三点弦测法按照弦长分割比例不同, 三点弦测法又分为三点等弦(Three-equal-point verse sine method, 3EVSM)和三点偏弦(Three-unequal-point verse sine method, 3UEVSM)两种。
三点等弦系统构成及原理如图 2所示。
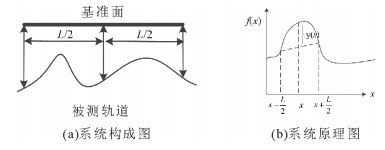
|
图 2 三点等弦示意图 Fig. 2 The schematic diagram of 3EVSM |
轨道实际不平顺值f(x)和弦测值y(x)之间的关系为
| $ y\left( x \right) = f\left( x \right) - \frac{1}{2}\left( {f\left( {x - \frac{L}{2}} \right) + f\left( {x + \frac{L}{2}} \right)} \right), $ | (3) |
转换到频域, 则
| $ \begin{array}{l} Y\left( \omega \right) = \\ F\left( \omega \right) - \frac{1}{2}\left( {F\left( \omega \right){{\rm{e}}^{ - {\rm{j}}\omega \frac{L}{2}}} + F\left( \omega \right){{\rm{e}}^{{\rm{j}}\omega \frac{L}{2}}}} \right) = \\ F\left( \omega \right) - F\left( \omega \right)\cos \omega \frac{L}{2} = \\ F\left( \omega \right)\left( {1 - \cos \omega \frac{L}{2}} \right) = F\left( \omega \right)H\left( \omega \right)。\end{array} $ | (4) |
其中,
三点偏弦系统构成及原理如图 3所示。
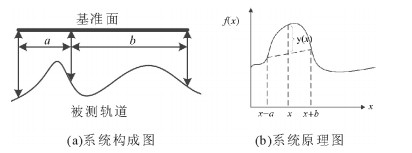
|
图 3 三点偏弦示意图 Fig. 3 The schematic diagram of 3UEVSM |
轨道实际不平顺值f(x)和弦测值y(x)之间的关系为
| $ y\left( x \right) = f\left( x \right) - \frac{b}{L}f\left( {x - a} \right) - \frac{a}{L}f\left( {x + b} \right), $ | (5) |
转换到频域, 则
| $ \begin{array}{l} Y\left( \omega \right) = \\ F\left( \omega \right) - \frac{b}{L}F\left( \omega \right){{\rm{e}}^{ - {\rm{j}}\omega a}} - \frac{a}{L}F\left( \omega \right){{\rm{e}}^{ - {\rm{j}}\omega b}} = \\ F\left( \omega \right)\left( {1 - \frac{b}{L}{{\rm{e}}^{ - {\rm{j}}\omega a}} - \frac{a}{L}{{\rm{e}}^{ - {\rm{j}}\omega b}}} \right) = \\ F\left( \omega \right)H\left( \omega \right)。\end{array} $ | (6) |
其中,
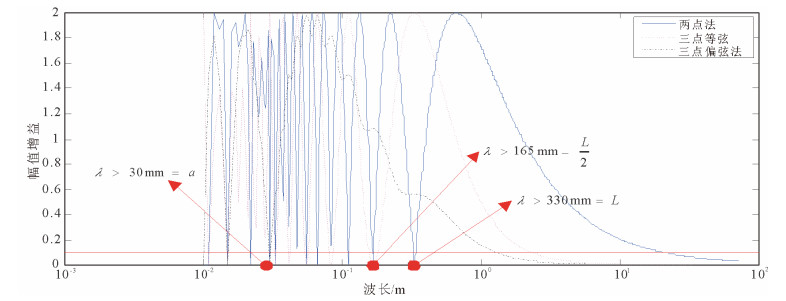
三种方法传递函数的幅频特性比较如图 4所示(设定弦长L=330mm,弦长分割比a:b=1:10)
|
图 4 3种方法传递函数的幅频特性 Fig. 4 The amplitudefrequency characteristics of transfer functions of the three chord-based methods |
观察图 4, 3种方法的传递函数幅值均不恒等于1。为使得检测波形逼近轨道真实状态, 通过逆滤波对弦测值进行二次处理, 即
| $ \left\{ \begin{array}{l} H\left( \omega \right){H_i}\left( \omega \right) = 1{{\rm{e}}^{ - {\rm{j}}\alpha \omega }},{\omega _1} \le \omega \le {\omega _2}\\ H\left( \omega \right) = 0。其他 \end{array} \right. $ | (7) |
其中,α为常数, 表示复原波形在时域的时延,[ω1, ω2]为波磨检测有效波段,Hi(ω)为逆滤波器的幅频响应。
在H(ω)=0时, 逆滤波失效。同时, 若传递函数幅值增益过小, 过度放大弦测值, 也会引起复原波形的剧烈振荡, 所以通常设定一个最低经验限值0.1[21]。由图 4可知, 两点弦对λ>L的大部分长波不平顺进行有效复原, 三点等弦对
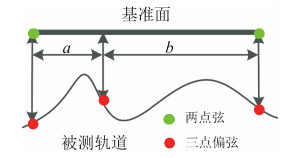
广域测量模型所用到的组合弦测量原理如图 5所示。在三点偏弦法的架构下, 首尾两个检测点构成的两点弦, 得到轨道长波不平顺的数据f(x)N。同时, 三点偏弦法本身用于对轨道的短波不平顺进行复原, 得到轨道短波不平顺的数据f(x)M。将短波不平顺的数据与长波不平顺的数据进行插值叠加处理, 从而实现单个系统下的全波段弦测波形的准确复原与测量。
| $ \begin{array}{l} f{\left( x \right)_{\max \left( {N,M} \right)}} = S{\left( {f{{\left( x \right)}_N}} \right)_{\max \left( {N,M} \right)}} + \\ S{\left( {f{{\left( x \right)}_M}} \right)_{\max \left( {N,M} \right)}}。\end{array} $ | (8) |
其中,N为长波复原数据的点数,M为短波复原数据的点数,S(·)为插值函数。
|
图 5 组合弦测原理图 Fig. 5 Principle diagram of combined chord measurement |
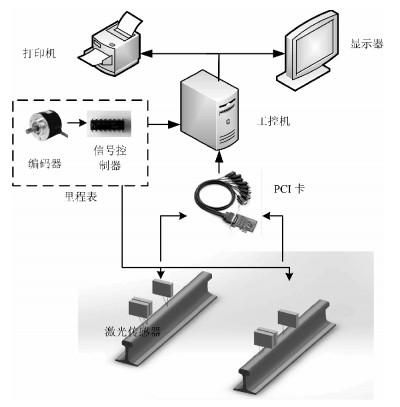
测量系统架构如图 6所示。系统采用两组共6台1D高精度位移激光传感器, 构成三点偏弦系统, 完成左右股钢轨波磨测量。车轴转动带动光电编码器旋转输出触发信号, 触发信号一方面发给信号处理器, 输出实时作业距离, 一方面发给左右股钢轨激光位移传感器, 完成多个传感器的同步等间隔采样。采集到的数据实时传递给计算机进行处理分析, 并且在显示器上直观地绘出处理还原后的波磨曲线。
|
图 6 测量系统架构 Fig. 6 The architecture of the combination-chord measurement system |
设整体弦长为L, 弦长分割比为a:b。由上节分析可知, a=30mm时, 三点偏弦可对λ>30mm的短波长成分进行有效复原, 所以只用选定整体弦长值L。取L分别为330mm,500mm,800mm,1 000mm, 绘出两点弦和三点偏弦幅频特性变化曲线如图 7所示, 复原波长的有效范围统计如表 1所示。
|
|
表 1 不同弦长下两种方法复原波长的有效范围 Tab. 1 The effective ranges of recovery wave lengths of the two methods under different chord lengths |

|
图 7 不同弦长下两种方法的传递函数幅频特性 Fig. 7 The amplitudefrequency characteristics of transfer function of the two methods under different chord lengths |
可以看出, 当L=1 000mm时, 三点偏弦的复原波长范围为30~2 000mm, 两点弦的复原弦长范围为1.2~63m, 两者的复原范围能够有效地重合, 满足30mm~60m波磨检测的全部有效波段需求。
2.2.2 基于LS的逆滤波器设计传统线性相位FIR逆滤波器设计采用频率采样法进行, 即
| $ {H_i}\left( \omega \right) = \left| {{H_i}\left( \omega \right)} \right|{{\rm{e}}^{{\rm{j}}{\theta _i}\left( \omega \right)}}。$ | (9) |
其中,
| $ {\theta _i}\left( \omega \right) = \pm \frac{{k{\rm{ \mathsf{ π} }}}}{2} - \tau \left( \omega \right)。$ | (10) |
其中,k=0为偶对称,k=1为奇对称,
| $ \left\{ \begin{array}{l} {\theta _i}\left( \omega \right) = - \alpha \omega ,3{\rm{EVSM}}\\ {\theta _i}\left( \omega \right) = - \frac{{\rm{ \mathsf{ π} }}}{2} - \left( {\alpha - L} \right)\omega ,2{\rm{VSM}} \end{array} \right. $ | (11) |
两点弦为奇对称, 三点等弦为偶对称。
对三点偏弦而言, 相频特性
| $ {\theta _i}\left( \omega \right) = a\tan \frac{{\frac{b}{L}\sin \omega a - \frac{a}{L}\sin \omega b}}{{1 - \frac{a}{L}\cos \omega b - \frac{b}{L}\cos \omega a}}, $ | (12) |
形式较为复杂, 转化为标准形式的运算量较大。
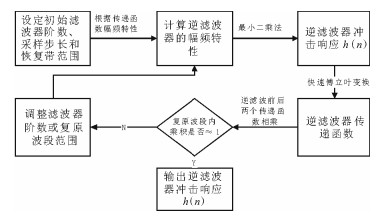
鉴于此, 本文采用最小二乘法设计逆滤波器。它在给定所期望的逆滤波器幅频响应Hi(ω)的基础上, 寻求一个期望幅频响应的近似Ĥi(ω), 使得在整个频域上, 误差信号的平方和∫[Ĥi(ω)-Hi(ω)]2dω达到最小。这种方法只需关注传递函数的幅频特性, 无需计算其相频特性, 优化了逆滤波器的设计流程。
基于最小二乘的逆滤波器设计步骤如图 8所示。
|
图 8 基于LS的逆滤波设计步骤 Fig. 8 The process chart of inverse filter based LS |
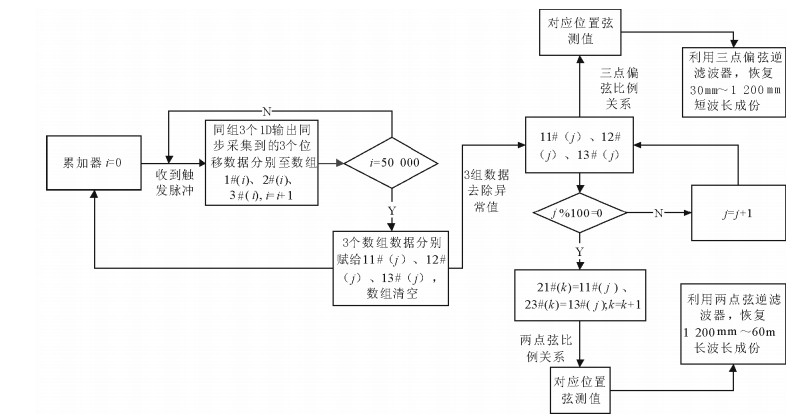
按照EN13231-3-2006规定, 每100m对钢轨平顺度进行一次评价。为了使弦测系统逆滤波前后两个传递函数乘积最接近1, 设定采样间隔2mm, 两点弦系统逆滤波器阶数为557, 三点偏弦系统逆滤波阶数为1 769。在得到3个测量点对应的3组数据后, 将首尾两组数据按照两点弦的200 mm采样间隔进行提取, 用于复原1.2~63m的长波长成份; 3组数据按照三点偏弦的2mm采样间隔进行提取, 用于复原30mm~2m的短波长成份。最后除去时延区间α, 将长短波相应有效里程区间的复原波形叠加, 得到最终的广域复原波形。复原流程如图 9所示。
|
图 9 弦测波形广域复原步骤图 Fig. 9 The wide-area recovery process of rail corrugation measured using chord-based method |
在Matlab平台随机使用7种不同波长的正弦波合成一段长为200m的轨道波磨原始波形, 即
| $ f\left( x \right) = \sum\limits_{i = 1}^7 {{A_i}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{{\lambda _i}}}x + {\phi _i}} \right)} 。$ | (13) |
各组谐波信息如表 2所示, 其中谐波1~4为短波长成份, 谐波5~7为长波长成份。
|
|
表 2 各组谐波信息 Tab. 2 Information of each harmonic |
弦测波形y(x)=f(x)ⓧh(x), 复原波形
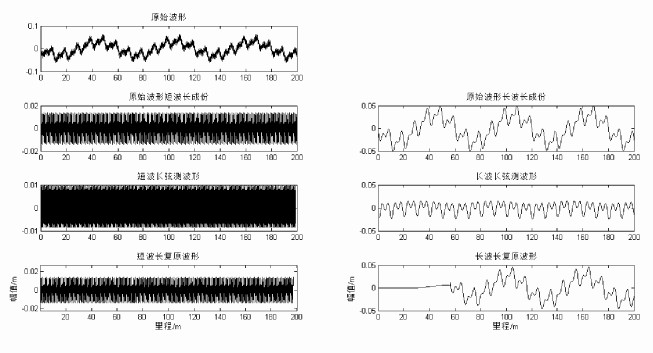
|
图 10 3种波形空域图 Fig. 10 Spatial graphs of the three waveforms |

|
图 11 原始波形与复原波形的频谱对比 Fig. 11 Spectrum comparison between the original and the recovery waveforms |
可以看出, 弦测波形与原始波形相差很大。但经过逆滤波后, 复原波形能够真实地逼近原始波形, 并且两者所在频谱一致。但是由于两点弦系统和三点弦系统采用不同的逆滤波器, 导致两个系统出现的延时不一致, 两点弦系统复原波形的延时远大于三点偏弦系统, 最后得到的叠加复原波形只能以长波长的延时为准。
为定量评估复原方法的准确性, 分别采用根均方误差(RMSE)、平均相对误差(MAPE)、相关系数(PPCC)作为评价指标, 对原始波形和复原波形有效里程区间内的短波长成份、长波长成份及合成波形进行统计, 结果如表 3所示。
| $ {\rm{RMSE = }}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \hat x} \right)}^2}} } , $ | (14) |
| $ {\rm{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{x_i} - \hat x}}{{{x_i}}}} \right| \times 100} , $ | (15) |
| $ {\rm{PPCC}} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} \cdot \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }}。$ | (16) |
|
|
表 3 复原前后数据偏差 Tab. 3 Data deviation before and after restoration |
可以看出, 原始波形和复原波形的相似度达到99%以上, 两者几乎完全重合。
合成波形是根据两点弦和三点偏弦的结果进行合成, 相比于传统的分离式测量系统, 在各自相对应的波段, 测量原理没有改变, 所以在两点弦和三点偏弦的复原波段精度并不会发生改变。
3.2 实际线路测试 3.2.1 实验平台搭建实验平台如图 12所示, 取一段长6m, 表面有锈蚀与现场钢轨反光特性相似的60型钢轨作为测量对象, 采用3个英国ZSY高精度1D激光位移传感器,按照本文三点偏弦架构搭建钢轨波磨测量系统(传感器的起始量程为25mm, 测量范围为70mm, 线性度0.1%), 整套系统固定于一个手推式轨检小车上, 通过人工推动对轨道起伏进行动态测量。

|
图 12 实际线路测试平台 Fig. 12 The measurement platform for the actual rails |
总测试里程为90m, 采样间隔0.002m, 对两侧轨道纵向起伏分别进行采集。同时, 利用图 13所示钢轨波磨尺对相应位置进行逐点测量, 作为波磨基准。

|
图 13 真实波磨测量 Fig. 13 Measurement of the real rail corrugations. |
两点弦系统还原长波形时存在58m的延时, 所以总复原波形的里程区间为0~32m。两侧轨道测量波磨与真实波磨对比如图 14所示。

|
图 14 复原波磨与真实波磨比较 Fig. 14 Comparison between the recovery and real corrugations |
可以看出, 测量波磨与真实波磨基本吻合。仍然分别采用根均方误差(RMSE)、平均相对误差(MAPE)、相关系数(PPCC)作为评价指标, 对两者的相似度进行统计, 结果如表 4所示。
|
|
表 4 复原前后数据偏差 Tab. 4 Data deviation before and after restoration |
本文主要针对30mm~60m波段的不平顺进行复原, 只需对小于30Hz的空间频率进行分析。两侧轨道测量频谱与真实频谱对比如图 15所示。
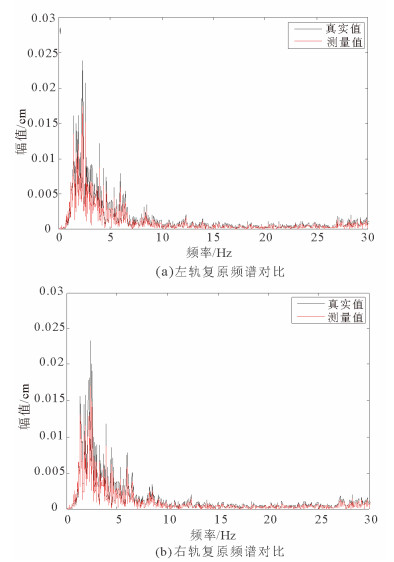
|
图 15 复原频谱与真实频谱比较 Fig. 15 Comparison between the recovery and real spectrums |
由于轨顶铁锈的影响, 测量波磨与真实波磨略有差异, 但两者的相似度仍然达到95.89%, 两者所在频谱也基本一致。表明本文方法具有较高的精度, 可用于工程测量。
4 结论1) 对不同速度的车辆和各个波段之间的关系进行分析可知,在30mm~60m波段的波磨都会对相关速度类型的车辆行驶产生不良影响。同时, 随着列车速度日益呈增长趋势, 由波磨问题引起的轨道维护工作量以及轨道维护成本也在不断加重, 因此, 广域波磨测量系统的实现与搭建对轨道全方面智能维护有着重要的现实意义。
2) 针对传统弦测法有效检测波段较窄, 不能对30mm~60m全波段弦测波形进行复原的缺陷, 本文提出一种基于两点弦与三点偏弦相结合的钢轨波磨广域测量方法。并且搭建了钢轨波磨广域测量系统, 实现了单个系统下全波段弦测波形的准确复原与测量。
3) 仿真与实际线路测试结果表明, 该方法能较为精确地对广域轨道波磨进行测量, 测量波磨与真实波磨所在频谱一致, 曲线基本吻合, 相似度达到95%以上。同时并不会降低传统测量系统单一波段下的测量精度。
4) 开展更为广泛的现场测量实验检验本文方法的效果, 并将其运用到实际工程中, 指导线路作业维护, 将是下一步工作的重点。
| [1] |
SATO Y, MATSUMOTO A, KNOTHE K. Review on rail corrugation studies[J]. Wear, 2002, 253(1): 130-139. |
| [2] |
罗林. 轨道随机干扰函数[J]. 中国铁道科学, 1982, 3(1): 74-110. |
| [3] |
ESVELD C. Measuring and rectifying rail roughness and bad welds[C]//Proceeding of 3rd Heavy Haul Railways Conference. Vancouver, 1986.
|
| [4] |
MOOLODOVA M, LI Z, DOLLEVOET R. Axle box acceleration: Measurement and simulation for detection of short track defects[J]. Wear, 2011, 271(1): 349-356. |
| [5] |
WANG A, COX S J. Effect of railpad stiffness on rail roughness growth and wayside noise levels on high speed track[C]//The 6th World Congress on Railway Research. Edinburgh, 2003.
|
| [6] |
张波, 刘启跃. 钢轨波磨的试验研究[J]. 铁道学报, 2003, 25(1): 104-108. |
| [7] |
聂蒙, 李建勇, 沈海阔, 等. 钢轨打磨压力波动的影响机理[J]. 中南大学学报(自然科学版), 2013, 44(8): 3546-3551. |
| [8] |
刘伶萍, 杜鹤亭, 杨爱红. 钢轨波浪磨耗检测系统的研究开发[J]. 中国铁道科学, 2002, 23(6): 65-69. |
| [9] |
GRASSIE S L. Measurement of railhead longitudinal profiles:A comparison of different techniques[J]. Wear, 1996, 191(1): 245-251. |
| [10] |
张国锋, 高晓蓉, 王黎, 等. 数字逆滤波技术在轨道不平顺检测中的应用[J]. 信号处理, 2004, 20(6): 667-670. |
| [11] |
HAN S. Measuring displacement signal with an accelerometer[J]. Journal of Mechanical Science and Technology, 2010, 24(6): 1329-1335. DOI:10.1007/s12206-010-0336-1 |
| [12] |
徐金辉, 王平, 汪力, 等. 轨道高低不平顺敏感波长的分布特征及其影响因素的研究[J]. 铁道学报, 2015, 37(7): 72-78. |
| [13] |
王前选, 梁习锋, 刘应龙, 等. 铁路钢轨视觉识别检测方法[J]. 中南大学学报(自然科学版), 2014, 45(7): 2496-2502. |
| [14] |
YOSHIMURA A. A new method for repairing railway track irregularities using levelling and lining machines[J]. WIT Transactions on the Built Environment, 1970, 20. |
| [15] |
CORREA N, VADILLO E G, SANTAMARIA J, et al. A versatile method in the space domain to study short-wave rail undulatory wear caused by rail surface defects[J]. Wear, 2016, 352: 196-208. |
| [16] |
宋寿鹏. 数字滤波器设计及工程应用[M]. 镇江: 江苏大学出版社, 2009.
|
| [17] |
GRASSIE S L. Rail corrugation: Advances in measurement, understanding and treatment[J]. Wear, 2005, 258(7): 1224-1234. |
| [18] |
吉村, 彰芳. 軌道狂い原波形の復元に関する理論的基礎の確立とその応用[J]. Railway Technical Research Report, 1987. |
| [19] |
YOSHIMURA A. Theory and practice for restoring an original waveform of a railway track irregularity[J]. Railway Technical Research Institute Quarterly Reports, 1995, 36: 85-94. |
| [20] |
李志彬, 刘宏立, 马子骥, 等. 斜率匹配波形延拓法抑制EMD端点效应[J]. 西北大学学报(自然科学版), 2016, 46(5): 673-679. |
| [21] |
程樱, 许玉德, 周宇, 等. 三点偏弦法复原轨面不平顺波形的理论及研究[J]. 华东交通大学学报, 2011, 28(1): 42-46. |
 2018, Vol. 48
2018, Vol. 48