随着智能生产的发展, 如何有效地从海量的标准生产数据集[1-3]中进行模式挖掘[4-9]来优化和指导智能生产已成为广泛研究的课题。Deng[4]等人提出了通过挖掘可替代模式(EP)来优化生产计划的问题, 即生产商生产由许多项目集(组件)组成的大量产品, 每个产品组件都有购买和存储的成本,当没有足够的成本资金时, 通过可替代模式挖掘找到可以去除的模式, 减少在某些条件下对工厂利润的损失, 管理者也可以利用可替代模式来制定新的生产计划, 但可替代模式在挖掘数量或设定阈值较大时会生成大量可替代封闭模式项目集, 占用大量的时间和内存, 降低了使用这种模式的智能系统的性能。
目前有很多挖掘可替代模式的算法, 如META, MERIT和MEI, META[4]是基于Apriori逐级生成候选模式的算法,算法执行时间过长,MERIT[2, 4-5]使用dNC-Sets结构的概念减少了内存消耗, 虽然使用dNC-Sets使MERIT比META有一些优势, 但仍然存在缺点。首先, 每个元素的权重值分别存储, 导致产生大量重复的可替代模式;其次,MERIT使用当且仅当X⊂Y时, X的dNC-Sets结构是Y的dNC-Sets结构的子集的策略, 此策略在各模式组合创建新节点时, 占用大量内存和执行时间。
为了优化可替代模式挖掘的内存消耗和算法执行时间, 本文基于利润参数提出了可替代封闭模式挖掘算法ECPM(Erasable closed patterns mining)。首先,根据定义的可替代规则[10]对数据进行预处理;其次,提出并证明了基于dNC-Sets结构[11-12]的可替代封闭模式定理;最后,基于该定理使用与哈希表技术相结合的分组策略实现了ECPM算法。实验结果表明, 对比META算法和MERIT算法, 在标准生产数据集中, ECPM算法在算法执行时间和内存消耗方面均有性能提升。
1 模型构建 1.1 定义及定理DB为一个标准的产品数据库,P={P1, P2,…,Pn}是DB中的产品集合, I={i1, i2,…,in}是所有的项目集, 每个产品以(Items, Val)的形式表示, Items表示产品项目集, Val表示该产品的利润, 表 1表示一个简单的产品数据库DB。
|
|
表 1 产品数据库DB Tab. 1 Product Database DB |
定义1 给定阀值ξ, 数据库DB, 定义可替代规则如下:
| $ g\left( X \right) \le T \times \xi , $ | (1) |
| $ g\left( X \right) = \sum\limits_{\left\{ {{P_k}\left| {X \cap {P_k}{\rm{Item}} \ne \emptyset } \right.} \right\}} {{P_k} \cdot {\rm{Val}}} , $ | (2) |
| $ T = \sum\limits_{{P_k} \in {\rm{DB}}} {{P_k} \cdot {\rm{Val}}} 。$ | (3) |
其中,X表示可替代模式, g(X)表示模式X的利润, T表示产品数据库DB的总利润。
基于定义1 Deng[4]提出了挖掘可替代模式(EP)的问题, 即找到所有的X使得g(X)<T×ξ, 通过例1来展示这个概念。
例1 对于表 1中的数据库,总利润T=
Le和Vo [12]基于WPPC树[11]提出了快速挖掘可替代封闭模式的dNC-Sets结构, WPPC树中的每个节点用项(名称, 权值, 子节点, 前序遍历节点数, 后序遍历节点数)来表示, 在WPPC中,节点Ni的节点编码表示为dNC=(前序遍历节点数, 后序遍历节点数, 权值), 项目集A的dNC-Sets结构表示为dNC(A), 是与A相关联的WPPC树中按递减前序遍历方式进行遍历的节点的编码集合, 当且仅当Ci·pre-order≤Cj·pre-order且Ci·post-order≥Cj·post-order时, 节点代码Ci是节点代码Cj的祖先节点, dNC-Sets p(X)表示为
| $ p\left( X \right) = \bigcup\limits_{A \in X} {p\left( A \right)} , $ |
A是模式X中的一个项目; p(A)是包含X的产品集合。
例2 针对表 1中的产品数据集可知, p(e)={2, 3, 4, 5, 6}, p(c)={3, 5}, p(f)={4, 6, 8}, 所以
| $ \begin{array}{l} p\left( {ec} \right) = p\left( e \right) \cup p\left( c \right) = \\ \left\{ {2,3,4,5,6} \right\} \cup \left\{ {2,3} \right\} = \left\{ {2,3,4,5,6} \right\}, \end{array} $ |
| $ \begin{array}{l} p\left( {ef} \right) = p\left( e \right) \cup p\left( f \right) = \\ \left\{ {2,3,4,5,6} \right\} \cup \left\{ {4,6,8} \right\} = \\ \left\{ {2,3,4,5,6,8} \right\}。\end{array} $ |
定义2 令XA和XB分别为将项目A和B连接X而获得的模式, dNC(XA),dNC(XB)和dNC(XAB)分别为XA,XB和XAB的dNC-Sets。XAB的dNC-Sets定义如下:
dNC(XAB)=dNC(XB)\dNC(XA)。表示dNC(XAB)是仅存在于p(XB)中而不存在于p(XA)中的产品标识符。
例3 由例2已知p(e),p(c),p(f), 所以
| $ {\rm{dP}}\left( {ec} \right) = p\left( c \right)\backslash p\left( e \right) = \emptyset , $ |
| $ {\rm{dNC}}\left( {ef} \right) = {\rm{dNC}}\left( f \right)\backslash {\rm{dNC}}\left( e \right) = \left\{ 8 \right\}, $ |
| $ {\rm{dNC}}\left( {ecf} \right) = {\rm{dNC}}\left( {ef} \right)\backslash {\rm{dNC}}\left( {ec} \right) = \left\{ 8 \right\}。$ |
定理1 XAB的利润可以基于XA的利润确定为
| $ g\left( {{X_{AB}}} \right) = g\left( {{X_A}} \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_{AB}}} \right)} {{P_k} \cdot {\rm{Val}}} 。$ |
其中,g(XA)是XA的利润,Pk·Val是产品Pk的利润, 在定理2中, X, A或B可以是空集, 当B=∅时, g(XA)=g(X)+
例4 对于表 1中的产品数据集, 由于
| $ p\left( e \right) = \left\{ {2,3,4,5,6} \right\},p\left( c \right) = \left\{ {3,5} \right\}, $ |
| $ p\left( f \right) = \left\{ {4,6,8} \right\},{\rm{dNC}}\left( {ec} \right) = \emptyset , $ |
| $ {\rm{dNC}}\left( {ef} \right) = \left\{ 8 \right\},{\rm{dNC}}\left( {ecf} \right) = \left\{ 8 \right\}, $ |
所以
| $ g\left( e \right) = 700\$ ,g\left( c \right) = 250\$ ,g\left( f \right) = 350\$ , $ |
| $ g\left( {ec} \right) = g\left( e \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {ec} \right)} {{P_k} \cdot {\rm{Val}}} = 700\$ , $ |
| $ g\left( {ef} \right) = g\left( e \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {ef} \right)} {{P_k} \cdot {\rm{Val}}} = 800\$ , $ |
| $ g\left( {ecf} \right) = g\left( {ec} \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {ecf} \right)} {{P_k} \cdot {\rm{Val}}} = 800\$ 。$ |
类似于频繁封闭模式[4, 6-7, 13]的定义, 利润不等于其超集的利润的可替代模式称为可替代封闭模式(ECP), 例如, 对上述DB挖掘EP, 当ξ=40%时, g(e)=g(ec)=700 < T×40%=780, 所以e和ec是两个可替代模式。又因为e的利润与其超集ec的利润相同, 所以e不是可替代封闭模式。
定理2 XA和XB分别为两个可替代模式, dNC(XA)和dNC(XB)分别为XA和XB的dNC-Sets结构, 则有以下4个属性:
1) 若dNC(XA)=dNC(XB),则
| $ g\left( {{X_A}} \right) = g\left( {{X_B}} \right) = g\left( {{X_{AB}}} \right); $ |
2) 若dNC(XA)⊂dNC(XB),则
| $ g\left( {{X_A}} \right) \ne g\left( {{X_B}} \right),g\left( {{X_B}} \right) = g\left( {{X_{AB}}} \right); $ |
3) 若dNC(XA)⊃dNC(XB),则
| $ g\left( {{X_A}} \right) \ne g\left( {{X_B}} \right),g\left( {{X_A}} \right) = g\left( {{X_{AB}}} \right); $ |
4) 若dPNC(XA)⊄dNC(XB), dNC(XB)⊄dNC(XA),则
| $ g\left( {{X_A}} \right) \ne g\left( {{X_B}} \right) \ne g\left( {{X_{AB}}} \right)。$ |
证明 分别证明4个属性:
1) 已知
| $ g\left( {{X_A}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
| $ g\left( {{X_B}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
当dNC(XA)=dNC(XB)时,
| $ g\left( {{X_A}} \right) = g\left( {{X_B}} \right), $ |
| $ {\rm{dNC}}\left( {{X_{AB}}} \right) = {\rm{dNC}}\left( {{X_B}} \right)\backslash {\rm{dNC}}\left( {{X_A}} \right) = \emptyset , $ |
所以
| $ \begin{array}{l} g\left( {{X_{AB}}} \right) = g\left( {{X_A}} \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_{AB}}} \right)} {{P_k} \cdot {\rm{Val}}} = \\ g\left( {{X_A}} \right) = g\left( {{X_B}} \right)。\end{array} $ |
2) 已知
| $ g\left( {{X_A}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
| $ g\left( {{X_B}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
当dNC(XA)⊂dNC(XB)时,
| $ g\left( {{X_A}} \right) < g\left( {{X_B}} \right), $ |
| $ \begin{array}{l} g\left( {{X_B}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} = \\ g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} - \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} + \\ \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} = g\left( {{X_A}} \right) + \\ \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_{AB}}} \right)} {{P_k} \cdot {\rm{Val}}} = g\left( {{X_{AB}}} \right)。\end{array} $ |
3) 已知
| $ g\left( {{X_A}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
| $ g\left( {{X_B}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
当dNC(XB)⊃dNC(XA)时,
| $ g\left( {{X_A}} \right) > g\left( {{X_B}} \right), $ |
| $ {\rm{dNC}}\left( {{X_{AB}}} \right) = {\rm{dNC}}\left( {{X_B}} \right)\backslash {\rm{dNC}}\left( {{X_A}} \right) = \emptyset , $ |
所以
| $ \begin{array}{l} g\left( {{X_{AB}}} \right) = g\left( {{X_A}} \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_{AB}}} \right)} {{P_k} \cdot {\rm{Val}}} = \\ g\left( {{X_A}} \right)。\end{array} $ |
4) 已知
| $ g\left( {{X_A}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
| $ g\left( {{X_B}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} , $ |
当dNC(XA)⊄dNC(XB),dNC(XB)⊄dNC(XA)时,
| $ g\left( {{X_A}} \right) \ne g\left( {{X_B}} \right), $ |
| $ \begin{array}{l} \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_{AB}}} \right)} {{P_k} \cdot {\rm{Val}}} \ne \\ \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} - \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} , \end{array} $ |
所以
| $ \begin{array}{l} g\left( {{X_{AB}}} \right) = g\left( {{X_A}} \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_{AB}}} \right)} {{P_k} \cdot {\rm{Val}}} > \\ g\left( {{X_A}} \right)。\end{array} $ |
| $ \begin{array}{l} g\left( {{X_B}} \right) = g\left( X \right) + \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} - \\ \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} = \\ g\left( {{X_A}} \right) - \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_A}} \right)} {{P_k} \cdot {\rm{Val}}} + \\ \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} , \end{array} $ |
| $ \sum\limits_{{P_k} \in {\rm{dNC}}\left( {{X_B}} \right)} {{P_k} \cdot {\rm{Val}}} \ne g\left( {{X_{AB}}} \right)。$ |
利用定理2, 当两个元素XA和XB与X有相同的前缀组合时, 有以下3种情况:
1) 如果dNC(XA)=dNC(XB), 则算法将XB移除并用XAB替换XA。
2) 如果dNC(XB)⊂dNC(XA), 则算法用XAB代替XA。
3) 否则, XA和XB都不会改变。
2 ECPM算法依据dNC-Sets结构可知当且仅当dNC(X)中的所有节点的祖先节点都在dNC(Y)中时,dNC(X)⊂dNC(Y), 所以,首先确定dNC-Sets结构及dNC(X)与dNC(Y)的关系, 其次, 根据定理3和dNC(X)与dNC(Y)的关系分析出可替代封闭模式(ECP), ECPM算法在Microsoft Visual Studio 2012中的C#和.Net Framework(版本4.5.50709)中编码。
2.1 确定dNC-Sets结构及模式间的关系输入:dNC(X)和dNC(Y)。
输出:dNC(XY),dNC(X)与dNC(Y)的关系。
r=3, i=0, j=0, dNC(XY)=∅, equal=0, countAB=0, countBA=0;
while i < |dNC(X)|, j < |dNC(Y)| do//两个数据集不为空//
begin while
if dNC(X)[i].PreOrder≤dNC(Y)[j].PreOrder then;
if dNC(X)[i].PostOrder≥dNC(Y)[j].PostOrder then;
//(X)[i]是(Y)[j]的祖先节点//
begin if
else countBA++, j++;
end if;
else i++; //判断数据集(X)[i]与(Y)[j]的关系//
else
if dNC(X)[i].PreOrder>dNC(Y)[j].PreOrder and
dNC(X)[i].PostOrder < dNC(Y)[j].PostOrder then
countAB++;
add dNC(Y)[j]to dNC(XY);
j++; //(Y)[j]是(X)[i]的祖节点//
end while;
while i < |dNC(X)| do
if |dNC(Y)|>0 and
dNC(X)[i].PreOrder>
dNC(Y) [|dNC(Y)|-1].PreOrder and
dNC(X)[i].PostOrder <
dNC(Y) [|dNC(Y)|-1].PreOrder then
countAB++, i++;
while j < |dNC(Y)| do
if |dNC(X)|>0 and
dNC(X) [|dNC(X)|-1].PreOrder>
dNC(Y)[j].PreOrder and
dNC(X) [|dNC(X)|-1].PostOrder <
countBA++;
add dNC(Y)[j]to dNC(XY);
j++;
if equal=|dNC(X)| and equal=|dNC(Y)| then
r=0;//dNC(X)=dNC(Y)//
else if countAB=|dNC(X)| then
r=1;//dNC(X) ⊂dNC(Y)//
else if countBA=|dP(Y)| then
r=2;//dNC(X) ⊃dNC(Y)//
return dNC(XY);
2.2 确定可替代封闭模式输入:标准生产数据集DB和阈值ξ。
输出:可替代封闭模式(ECP)。
Scan DB to construct WPPC-tree with threshold ξ and determine E1;
Generate dPidset of E1;
Let Hashtabe=∅
be a hashtable for storing the indexes of ECP;
if E1 has more than element, call dP-expand-E(E1);
Procedure dP-expand-E(Ev);
for i←0 to |Ev|do
begin for
Enext←∅;
for j←i+1 to|Ev|do
begin for
(dNC-Set(ECP)andr)←NC-Diff(dNC-Set (Ev[j]), dNC-Set (Ev[i]))
if g(ECP)≤ξ×T then//满足可替代规则//
if r=0 then;
Ev[i]=Ev[i]∪Ev[j];
update Enext;
remove Ev[j];
j--; //两个数据集项目集相同, 求交集后去除Ev[j]
else if r=2 then
Ev[i]=Ev[i]∪Ev[j];
update Enext
else if r=1 then//Ev[i]是Ev[j]的子集//
ECP=Ev[i]∪Ev[j];
add ECP to Enext;
remove Ev[j];
else ECP=Ev[i]∪Ev[j];
add ECP to Enext;
end for;
if dP-check-closed-property (Ev[i])
then
Eresult←Ev[i]; //检查封闭性
add Ev[i]to hashtable with g(Ev[i]) asthe key;
if |Enext| ≥ 1 then
expand-E(Enext)
end for;
function dP-check-closed-property(EP);
ECP←hashtable[g(EP)]; //ECP储存可替代封闭模式//
if ECP is not null then
for each ECP in ECPs do
if EP⊂ECP then//可替代模式集属于可替代封闭模式集。
return false;
return ture;
为了更好地理解ECPM算法, 使用前面例子中的数据集DB举例, 具体步骤如下:
1) 扫描DB一次, 找出ξ=40%时的所有可替代项目及其dNC-Setst结构。
2) 项目e依次与d, f, h和c组合。ed, eh和ef将由于阈值而被消除, 由于dNC(c)⊂dNC(e), e根据定理3替换为ec。
3) 项目d反复与h, f和c组合。由于dNC(f)⊂dNC(d)及dNC(h)⊂dNC(d), d被替换为dfh, 再考虑与c组合,由于g(dfhc)= 750,小于给定阈值时的利润, 所以算法为ECP创建新节点dfhc。
4) f与h和c组合, 分别产生fh和fc。使用fh和fc来创建fhc, 然而, 因为dfhc是fhc的超集且具有相同的利润(750), 所以fhc被排除, h与c结合创建hc。
图 1表示上述4个步骤的具体过程。
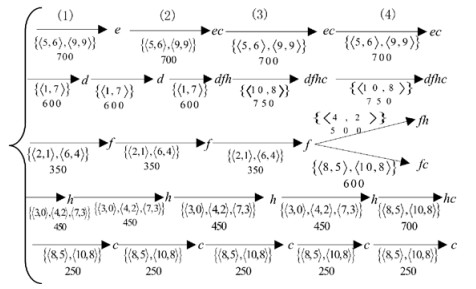
|
图 1 算法具体步骤 Fig. 1 Algorithm specific step |
对表 1的标准生产数据集DB进行可替代封闭模式算法(ECPM)分析, 得出当ξ=40%时,DB中所有的可替代封闭模式及各模式的利润如表 2所示。
|
|
表 2 DB中当ξ=40%所有可替代封闭模式 Tab. 2 All ECP for DB with ξ=40% |
为了验证本文所提算法的性能, 将算法ECPM与常规类似算法MERIT和Na-MEI在4个曾被大量的关联规则挖掘算法用于仿真比较的标准生产数据库中进行实验, 其中两个是稀疏型数据库Accidents和Pumsb[13-15], 另外两个是来自IBM的密集型数据库T10I4D100K和Connect[14, 9], 实验中对算法执行时间和内存消耗两个指标进行了分析算法运行环境:Windows10系统, 2.3GHz CPU, 8G内存, 表 3是仿真数据库的数据特征。
|
|
表 3 仿真所用数据库 Tab. 3 The simulation dataase |
图 2显示了不同阈值下ECPM算法、MERIT算法与META算法在标准生产数据库Accidents,Pumsb,T10I4D100K和Connect中的算法执行时间,由图 2可知,在这些标准生产数据库中,ECPM算法的执行时间明显优于META和MERIT算法,且当ξ= 0.0007,0.0045,0.07,1.5时,META算法的执行时间远远大于ECPM算法的执行时间,虽然META是Apriori算法的升级算法,依然会产生大量的候选项集,由于内存限制,当阈值较大时META算法将无法运行。
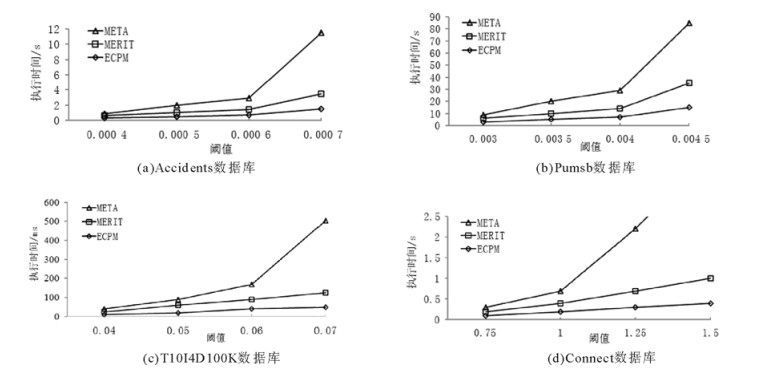
|
图 2 Accidents, Rumsb, T10I4D100K和Connect中ECPM算法与其他算法的执行时间 Fig. 2 Execution time of ECPM and other algorithms for Accidents, Rumsb, T10I4D100K and Connect |
图 3显示了在标准生产数据集Accidents,Pumsb,T10I4D100K和Connect中,ECPM算法、MERIT算法与META算法关于内存消耗的分析。随着规定阈值的增大, 内存消耗也随之增加, 当阈值较大时, MERIT和META算法占用存几乎ECPM算法的两倍。
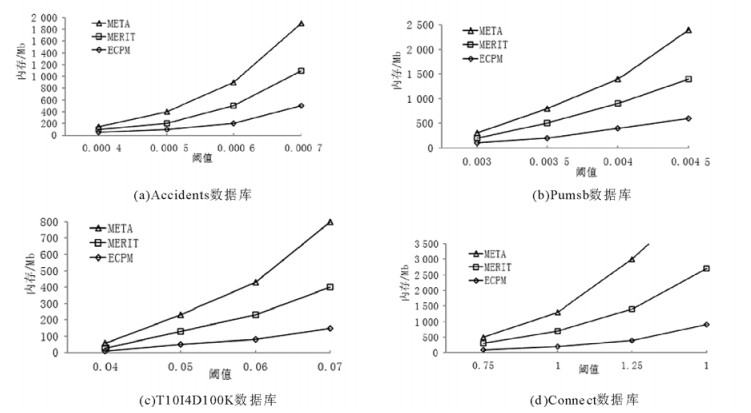
|
图 3 Accidents, Pumsb, T10I4D100K和Connect中ECPM算法与其他算法的内存消耗 Fig. 3 Memory consumption of ECPM algorithms and other algorithms for Accidents, Pumsb, T10I4D100K and Connect |
从海量的标准生产数据集中分析可替代封闭模式来指导和优化智能生产是重要的研究领域, 为了降低算法执行时间和内存消耗, 本文提出一种可替代封闭模式挖掘算法(ECPM),首先,通过定义的可替代规则对生产数据集进行预处理, 其次, 依据标准dNC-Sets数据结构特性确定各模式的dNC-Sets结构及各模式间的关系, 最后根据已证明的可替代封闭模式定理基于利润参数挖掘出可替代封闭模式, 与传统的META算法和MERIT算法对比,ECPM算法在保证获得产品部件的最优组合的同时,在执行时间和内存占用方面均有性能提升。
| [1] |
刘云, 向禅. 基于虚构理论对不平衡数据集中少数类关联规则挖掘的研究[J]. 云南大学学报(自然科学版), 2017, 39(4): 33-38. |
| [2] |
梁珺, 刘云. 基于析取规则对不确定数据挖掘的优化研究[J]. 四川大学学报(自然科学版), 2016, 53(4): 788-792. |
| [3] |
NGUYEN G, LE T, VO B, et al. EIFDD: An efficient approach for erasable itemset mining of very dense datasets[J]. Applied Intelligence, 2015, 43(1): 85-94. |
| [4] |
DENG Z H, FANG G D, WANG Z H, et al. Mining erasable itemsets[C]//International Conference on Machine Learning and Cybernetics. IEEE, 2009: 67-73.
|
| [5] |
VO B, LE T, COENEN F, et al. Mining frequent itemsets using the N-list and subsume concepts[J]. International Journal of Machine Learning & Cybernetics, 2016, 7(2): 253-265. |
| [6] |
HUYNH-THI-LE Q, LE T, VO B, et al. An efficient and effective algorithm for mining top-rank-k, frequent patterns[J]. Expert Systems with Applications, 2015, 42(1): 156-164. DOI:10.1016/j.eswa.2014.07.045 |
| [7] |
VRANIC M, PINTAR D, BANEK M. Towards better understanding of frequent itemset relationships through tree-like data structures[J]. Expert Systems with Applications, 2015, 42(3): 1717-1729. DOI:10.1016/j.eswa.2014.09.040 |
| [8] |
DENG Z. Mining top-rank-k, erasable itemsets by PID_lists[J]. International Journal of Intelligent Systems, 2013, 28(4): 366-379. DOI:10.1002/int.2013.28.issue-4 |
| [9] |
DAM T L, LI K, FOURNIER-VIGER P, et al. An efficient algorithm for mining top-rank-k, frequent patterns[J]. Applied Intelligence, 2016, 45(1): 96-111. |
| [10] |
NGUYEN G, LE T, VO B, et al. Discovering erasable closed patterns[C]//Asian Conference on Intelligent Information and Database Systems. Springer, 2015: 368-376.
|
| [11] |
YUN U, LEE G. Sliding window based weighted erasable stream pattern mining for stream data applications[J]. Future Generation Computer Systems, 2016, 59: 1-20. DOI:10.1016/j.future.2015.12.012 |
| [12] |
LE T, VO B, COENEN F. An efficient algorithm for mining erasable itemsets using the difference of NC-Sets[C]//IEEE International Conference on Systems, Man, and Cybernetics. IEEE, 2014: 2270-2274.
|
| [13] |
赵官宝, 刘云. 一种基于位表的有效频繁项集挖掘算法[J]. 山东大学学报(理学版), 2015(5): 23-29. |
| [14] |
NGUYEN L T T, NGUYEN N T. An improved algorithm for mining class association rules using the difference of Obidsets[J]. Expert Systems with Applications, 2015, 42(9): 4361-4369. DOI:10.1016/j.eswa.2015.01.002 |
| [15] |
NGUYEN L T T, NGUYEN N T. Updating mined class association rules for record insertion[J]. Applied Intelligence, 2015, 42(4): 707-721. DOI:10.1007/s10489-014-0614-1 |
 2018, Vol. 48
2018, Vol. 48
