2. 西北大学 信息科学与技术学院, 陕西 西安 710127
2. School of Information Science and Technology, Northwest University, Xi′an 710127, China
单幅图像超分辨率重构(Single image super-resolution, SISR)是指利用一幅低分辨率(Low resolution, LR)图像来重构出具有高像素密度并且具有更丰富的细节信息的高分辨率(High resolution, HR)图像。传统的图像采集系统受硬件设备的限制或者拍摄场景、环境和天气等因素的影响, 所获得的图像分辨率往往比较低,且清晰度较差, 参考价值不高, 极大地限制了所获得图像的应用范围。图像超分辨率(Super resolution, SR)作为一种能够突破成像系统固有分辨率,并且能显著提高图像质量的方法, 在视频监控、医学成像和遥感图像等领域中有着广泛的应用。
一幅低分辨率图像zl∈RNl×Ml可以看作是由高分辨率图像yh∈RNh×Mh经过模糊化及下采样而得到的, 即
| $ {z_{\rm{l}}} = {S^ \downarrow }\left( {h*{y_{\rm{h}}}} \right)。$ |
其中,h和S↓分别是模糊化和下采样算子[1]。相对于yh而言, 图像zl的退化主要表现在边缘模糊化和纹理细节的丢失。如果对zl进行某种S-R操作, 使输出图像
| $ \hat y = S-R\left( z \right) \approx {y_{\rm{h}}}, $ |
则实现了对zl的超分辨率重构。从数学上来看, 图像超分辨重构问题是一个明显的病态逆问题, 必须利用合理的先验假设进行正则化。基于图像具有局部平滑性的先验假设, 图像超分辨率重构的早期研究围绕插值技术展开, 1978年Hou等人[2]提出的样条插值技术,包括最近邻插值、双线性插值和双三次插值等, 由于其简单易行, 至今仍被广泛使用。但是, 插值只是增加了图像像素数目, 并不能在真正意义上增强图像的分辨率。随着插值后图像中高频成分的进一步减少, 将带来图像边缘模糊化和锯齿化等效应。为了改善插值的效果, Dai等人[3]提出的沿着图像边缘进行插值的方法,以及Zhang等人[4]提出的自适应方向滤波器方法, 能够在插值的同时,在一定程度上保持图像边缘的光顺和锐利。
基于样本学习的图像超分辨率重构通过低分辨率/高分辨率(LR/HR)图像对构成的训练样本集合建立两者之间的对应关系[5-8]。文献[8]通过在事先构造的LR图像块数据集中寻找误差最小的图像块来对LR图像进行表达, 然后在HR图像块数据集中选取与之相对应的图像块来完成HR图像的重构。Yang等人最先将信号的稀疏表示理论应用到基于样本学习的图像超分辨率中[9-11], 其核心思想是训练一对LR/HR字典, 通过求解LR图像块在LR字典中的稀疏表示, 对HR字典中的原子(图像块)进行线性组合, 重构出对应的HR图像块。Zeyde等[12]对Yang等人的方法做了改进, 采用K奇异值分解算法(K-singular value decomposition, K-SVD)和正交匹配追踪算法(Orthogonal matching pursuit, OMP)完成字典的训练和稀疏编码, 大大简化了算法的结构和计算复杂度。文献[13]提出了一种基于双重稀疏性字典的SISR方法, 其特点是训练字典的样本数据集取自样本图像的小波变换域, 因而具有双重稀疏性的优点, 即可以在只有少量样本图像的情况下, 获得较好的重构效果。
然而, 通过对有限样本图像的学习所得到的字典适用范围有限。为了提高字典的普适性, 必须利用大量的样本图像进行训练, 这使得字典的学习效率降低。此外, 当用于字典训练的样本图像与待处理LR图像结构相似度较低时, 这种方法并不能完全保证所获得HR图像中高分辨率细节的准确性和可靠性。基于图像结构自相似性的SR方法则能够在一定程度上克服上述基于样本学习方法的问题, 这类方法能够在没有任何高分辨率训练样本的情况下, 完成LR图像的超分辨率重构。文献[14]利用待重构LR图像自身所包含的低频成分和高频成分产生两个对应的码本, 通过在低频码本中寻找与插值后的LR图像最相似的码元, 将其对应的高频码元作为附加信息加入插值后的图像来获得HR图像。文献[15]利用图像的多尺度结构自相似性, 通过对相同尺度和不同尺度下LR图像中相似图像块的学习来完成低分辨率图像的超分辨率重构。Zeyde等人将图像的多尺度结构自相似性与基于稀疏表示的SR方法相结合, 提出了低分辨率图像的自举算法(Bootstrapping method), 该算法在没有任何训练样本图像的情况下, 将待处理的LR图像视作高分辨率样本, 将LR图像的进一步模糊化下采样图像视作低分辨率样本, 构建LR/HR样本数据集,训练一对字典。文献[16]通过计算样本图像块的均方误差, 对训练样本数据集进行筛选, 大幅减少了训练字典的原子数, 该算法能够在保持重构效果的同时显著提高算法的效率。基于图像结构自相似性的SR算法的优点是不需要任何样本图像, 仅通过对输入LR图像自身进行学习来完成超分辨率重构, 具有一定的高效性和自适应性, 然而,由于LR图像在形成过程中已经丢失了大量高分辨率细节, 通过对自身信息的学习所提取出的高频成分有限, 因而重构效果有待提高。文献[17]提出了一种SISR算法, 该方法在训练字典的过程中, 首先,对LR训练样本图像采用Zeyde等人提出的自举算法进行超分辨率重构, 然后,将自举重构输出图像与LR和HR训练样本图像求差, 并将两幅差值图像作为样本数据源训练一对字典。本文将在文献[17]的基础上, 进一步对两幅差值图像作一级不做下采样的小波变换, 并将4个方向的小波分解系数作为样本数据源,训练具有双重稀疏性的字典对, 完成单幅图像的超分辨率重构。
1 基于稀疏表示的SISR算法 1.1 基于稀疏表示的SISR算法框架图像的稀疏表示是指图像(块)可完全或近似地由非常少的一组原子(Atom)图像(块)的线性组合表示, 而所有的原子图像(块)则组成一个过完备字典。基于图像的稀疏表示的SISR方法, 其假定取自高分辨率图像yh的任意一个图像块phk ∈Rn可以表示为
| $ p_{\rm{h}}^k \approx {\mathit{\boldsymbol{D}}_{\rm{h}}}{\mathit{\boldsymbol{\alpha }}^k}。$ | (1) |
其中,Dh∈Rn×K为高分辨率字典,k为字典的原子总数, αk为phk在字典Dh下的稀疏表示向量, 并且满足‖αk‖0
| $ p_{\rm{l}}^k = Lp_{\rm{h}}^k = L{\mathit{\boldsymbol{D}}_{\rm{h}}}{\mathit{\boldsymbol{\alpha }}^k} = {\mathit{\boldsymbol{D}}_{\rm{l}}}{\mathit{\boldsymbol{\alpha }}^k}。$ | (2) |
其中,L代表通过高分辨率图像块phk产生其对应的低分辨率图像块plk的算子。
从式(2)可以看出, 假如字典Dl和Dh满足
| $ {\mathit{\boldsymbol{D}}_1} = L{\mathit{\boldsymbol{D}}_{\rm{h}}}, $ | (3) |
那么低分辨率图像块plk在字典Dl下的稀疏表示向量也为αk, 这意味着如果可以训练得到具备Dl=LDh这一特性的字典对{Dl, Dh}, 那么只要找到低分辨率图像块plk在Dl下的稀疏表示向量αk, 就可以利用式(1)重构出对应的高分辨率图像块。由此可见, 基于稀疏表示和字典学习的SISR方法成功的关键, 就在于满足式(3)的字典对{Dl, Dh}的训练。
文献[10]建议的{Dl, Dh}由取自LR/HR图像的原始图像块对构成, 其中Dl=[plk, k=1, 2, …, C],Dh=[phk, k=1, 2, …, C], C表示样本数。由于所需的样本数很大(C≈106), 求解稀疏表示向量αk的计算量十分繁重。
为了解决这一问题, Yang等在文献[11]中进一步提出通过样本对集合{Xh, Xl}来训练紧凑的字典对, 即通过求解下列最优化问题
| $ \begin{array}{l} \left\{ \begin{array}{l} {\mathit{\boldsymbol{D}}_{\rm{h}}} = \mathop {\min }\limits_{{\mathit{\boldsymbol{D}}_{\rm{h}}}, \mathit{\boldsymbol{A}}} \left\| {{\mathit{\boldsymbol{X}}_{\rm{h}}}-{\mathit{\boldsymbol{D}}_{\rm{h}}}\mathit{\boldsymbol{A}}} \right\|_F^2, \\ {\mathit{\boldsymbol{D}}_{\rm{l}}} = \mathop {\min }\limits_{{\mathit{\boldsymbol{D}}_{\rm{l}}}, \mathit{\boldsymbol{A}}} \left\| {{\mathit{\boldsymbol{X}}_{\rm{l}}}-{\mathit{\boldsymbol{D}}_{\rm{l}}}\mathit{\boldsymbol{A}}} \right\|_F^2, \end{array} \right.\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\left\| {{\mathit{\boldsymbol{\alpha }}_i}} \right\|_0} \le {K_0}, i = 1, \cdots, C。\end{array} $ | (4) |
得到{Dl, Dh}。其中,样本数据集Xh取自HR样本图像中大小为
Zeyde等对训练过程作了如下改进:①利用主成分分析法(Principle component analysis, PCA)对低分辨率样本数据xlk进行降维处理, 以加速训练过程; ②HR样本数据集Xh不是直接取自HR样本图像, 而是取自HR图像与LR图像的差; ③利用Xl, 采用K-SVD算法[18]和OMP算法来完成字典Dl(∈R4n×K, K为字典的原子总数)的训练和稀疏表示向量的求解, 然后,将得到的稀疏表示矩阵A作为已知数代入式(5),获得HR字典,
| $ {\mathit{\boldsymbol{D}}_{\rm{h}}} = {\mathit{\boldsymbol{X}}_{\rm{h}}}{\mathit{\boldsymbol{A}}^ + } = {\mathit{\boldsymbol{X}}_{\rm{h}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)^{-1}}。$ | (5) |
双重稀疏性字典[1]定义为
| $ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} B}}。$ | (6) |
其中,Φ为已知的具有快速实现算法的隐式字典, B为稀疏表示矩阵, 可见对字典D的训练便转化为求解稀疏表示矩阵B的问题。文献[19]中将Φ具体化为正交小波变换,因此有
| $ \begin{array}{l} \left\| {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{DA}}} \right\|_2^2 = \left\| {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{ \boldsymbol{\varPhi} BA}}} \right\|_2^2 = \\ \left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{BA}}} \right\|_2^2 = \left\| {\mathit{\boldsymbol{W}} - \mathit{\boldsymbol{BA}}} \right\|_2^2。\end{array} $ | (7) |
其中,W=ΦTX为样本数据X的小波变换系数。可见, 训练B的任务可通过求解下列最优化问题来实现,
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \mathop {\min }\limits_{\mathit{\boldsymbol{B}}, \mathit{\boldsymbol{A}}} \left\| {\mathit{\boldsymbol{W}}-\mathit{\boldsymbol{BA}}} \right\|_F^2, \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\left| {{\mathit{\boldsymbol{\alpha }}_t}} \right|_0} \le {K_0}, t = 1, \cdots, T。\end{array} $ | (8) |
与式(4)比较可知, 只要用小波分解系数W取代原来的样本数据集X, 采用相同的K-SVD算法即可学习得到具有双重稀疏性的字典B。文献[13]采用的LR训练样本数据集, 来源于LR图像经过一级平稳小波变换后的4个分量图像:La, Lh, Lv, Ld。为了充分利用近似分量La中所包含的高频信息, 对La施以拉普拉斯变换
| $ {\nabla ^2}\left( {{L_{\rm{a}}}} \right) = {\partial _{xx}}\left( {{L_{\rm{a}}}} \right) + {\partial _{yy}}\left( {{L_{\rm{a}}}} \right)。$ | (9) |
考虑到∇2(La)和Lh, Lv, Ld比较, 信号强度有很大差别, 故根据经验及实验结果比较, 选取两个加权系数ξ1和ξ2, 分别与∇2(La)和Ld相乘, 以使4个特征分量图像之间取得平衡。在HR字典训练阶段, 采用的训练样本集与Zeyde等人建议的一样, 取自与LR图像与HR图像的差。
有了LR/HR训练样本数据集以后, 采用K-SVD算法训练得到一对LR/HR字典{Dl, Dh}, 利用OMP算法求解LR图像在Dl下的稀疏表示矩阵A, 重构出的HR图像数据集合为
| $ \mathit{\boldsymbol{\hat X}} = {\mathit{\boldsymbol{D}}_{\rm{h}}}*\mathit{\boldsymbol{A}}。$ | (10) |
将
正如文献[19]中所指出的, 与普通的训练字典相比较, 双重稀疏性字典具有更显著的高效性和紧凑性, 这是由于它的训练样本数据本身已是稀疏化后的小波变换系数, 从而在训练样本较少的条件下, 便可获得具有较强普适性的字典。
2 结合低分辨率图像自举和双重稀疏性字典训练的SISR算法 2.1 低分辨率图像自举算法由于自然图像的局部结构在不同区域常常重复出现, 其所具有的这种结构自相似性(Structural self-similarities)在相同尺度以及不同尺度下仍然保持不变, 即图像中的图像块会在其相同尺度以及不同尺度的图像中反复多次出现, 当图像块较小时(譬如5×5)这种性质尤为突出[15]。这样一来, 以图像的自相似性作为正则化约束, 在没有任何其他训练样本的情况下, 仍可以完成低分辨率图像的超分辨率重构。Zeyde等人结合图像的结构自相似性, 在基于稀疏表示的SISR方法框架下, 提出了一种单幅图像超分辨率重构的自举算法[12], 其具体原理如图 1所示。
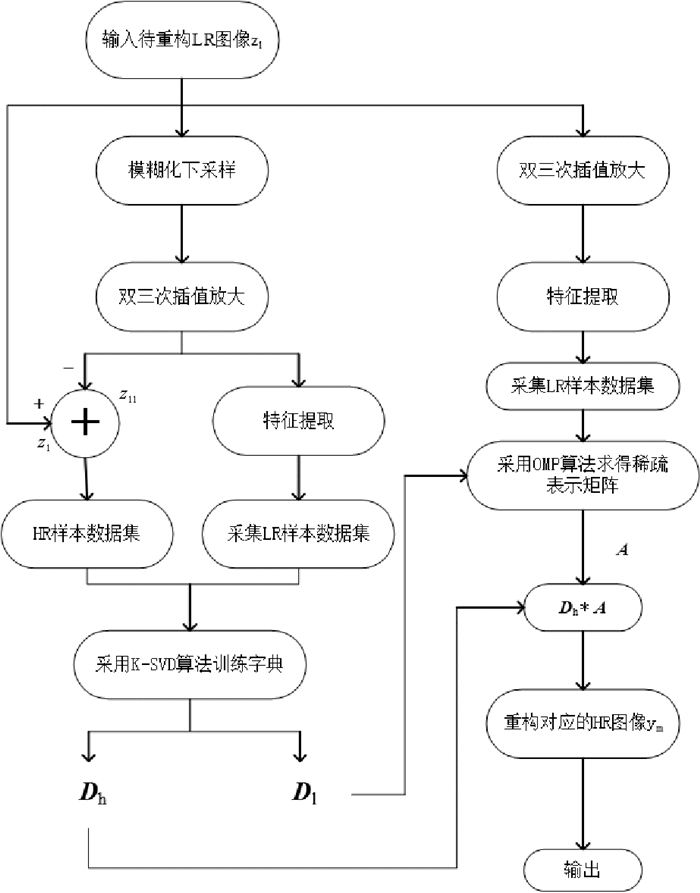
|
图 1 Zeyde等人提出的“自举”算法原理图 Fig. 1 The scheme diagram of the bootstrapping algorithm proposed by Zeyde |
该自举算法在没有任何HR训练样本图像的情况下, 将待重构的LR图像z作为HR训练样本图像, 将z的进一步模糊化下采样图像zl作为LR训练样本图像, 针对构建的“LR/HR”训练样本对, 利用K-SVD算法训练得到一对字典, 从而完成对LR图像z的超分辨率重构。实验证明, 自举算法的重构效果优于传统的双三次插值等方法, 并且在许多应用场合下堪比甚至优于基于样本学习的SISR方法[12]。
为了进一步提高SISR算法的重构效果, 本文提出结合低分辨率图像自举和双重稀疏性字典训练的算法模型, 下面将对本文的SISR方法的整体流程进行描述。
2.2 结合低分辨率图像自举和双重稀疏性字典的训练方法首先, 本文利用如图 1所示的自举算法对LR训练样本图像yl进行s倍的超分辨率重构, 重构输出图像记作ym。然后采用式(11)来计算自举图像与LR,HR训练样本图像的差,
| $ \left\{ {\begin{array}{*{20}{l}} {{e_1} = {y_{\rm{m}}} - {y_1},}\\ {{e_{\rm{h}}} = {y_{\rm{h}}} - {y_{\rm{m}}}。} \end{array}} \right. $ | (11) |
结合文献[13]提出的双重稀疏性字典的训练方法, 进一步对el和eh作一级不做下采样的平稳小波变换(Stationary wavelet transform, SWT),来实现对差值图像的特征提取, 分别得到el和eh的近似、水平、垂直和对角线方向的小波分解系数Lal,Lhl,Lvl,Ldl和Lah,Lhh,Lvh,Ldh, 由此可构成4对LR,HR训练样本图像:{Lal,Lah},{Lhl,Lhh},{Lvl,Lvh}和{Ldl,Ldh}。
采用一个大小为
对于水平、垂直和对角线方向的LR,HR训练样本图像对, 采用相同的方法生成相应的样本数据集合{Xhl, Xhh},{Xvl, Xvh}和{Xdl, Xdh}, 采用同样的字典训练方法就可得到水平、垂直和对角线分量的字典对{Dhl, Dhh},{Dvl, Dvh}和{Ddl, Ddh}。
2.3 图像重构阶段在重构阶段,首先,对重构LR图像zl采用图 1所示的自举算法完成一次s倍的超分辨率重构, 得到ym′, 然后,根据公式el′=ym′-zl计算出差值图像el′。对el′作一级不做下采样的SWT分解, 得到el′的4个方向的小波分解系数Lal′, Lhl′, Lvl′和Ldl′。沿着图像Lal′, 采用大小为
对集合Xal′采用OMP算法求出其在近似分量LR字典Dal下的稀疏表示矩阵Aa′, 再利用对应的HR字典Dah重构出近似分量图像,
| $ {\mathit{\boldsymbol{\hat X}}_{\rm{a}}} = {\mathit{\boldsymbol{D}}_{{\rm{ah}}}}*{\mathit{\boldsymbol{A'}}_{\rm{a}}}。$ |
针对Lhl′,Lvl′和Ldl′采用相同的方法构建测试样本数据集Xhl′,Xvl′和Xdl′, 利用字典对{Dhl, Dhh},{Dvl, Dvh}和{Ddl, Ddh}即可重构出其他3个小波分解系数图像
| $ \hat y = {y'_{\rm{m}}} + {e'_{\rm{h}}}。$ |
可以看出, 本文提出的SISR方法是对文献[17]提出方法的改进。通过进一步求取差值图像eh和el的4个方向的小波分解系数, 来构建4组LR/HR样本数据集,并分别训练4对字典。由于训练字典的数据源取自差值图像的小波变换域, 因而具有双重稀疏性字典的优点, 同时能够通过恢复出各个小波分解系数图像中更多的细节信息提高重构的质量。
3 实验结果在实验过程中, 将本文算法的超分辨率结果与双三次插值算法,Zeyde等人提出的SISR方法和文献[17]提出的SISR算法进行对比。本文采用的HR训练图像集如图 2所示, 对其进行模糊化下采样即可生成相应的而LR训练图像集, 在该过程中所采用的模糊化函数由一维数字滤波器

|
图 2 训练图像集 Fig. 2 Training images |

|
图 3 测试图像集 Fig. 3 Testing images |
在构建训练样本数据集时, 首先采用图 1所示的自举算法对LR训练样本图像进行一次超分辨率重构, 得到与HR训练样本图像大小相同, 但分辨率较低的自举输出图像。按照式(11)计算两个差值图像, 采用Haar小波对两个差值图像作一级不做下采样的SWT变换, 然后即可按2.2节所述方法构建训练样本数据集。实验中选用的窗口大小为7×7, 同时为了避免边界效应, 在对图像块数据进行采集时, 去掉了靠近上下边界的各5行和靠近左右边界的各5列。在训练字典的过程中, 设定字典中原子的数目K=512, 稀疏表示向量中非零元素的个数K0=3, K-SVD算法迭代次数t=50。
当s=2时, 训练得到的4个方向小波分解系数的LR和HR字典如图 4所示, 图 5是采用几种不同SR方法进行重构所得结果的对比。

|
图 4 训练得到的4个方向小波分解系数的LR和HR字典(s=2) Fig. 4 Four pairs of LR and HR dictionaries trained using the four pairs of wavelet coefficients(s=2) |

|
图 5 几种方法的重构实验结果对比(s=2), 从左到右依次为:bicubic插值,Zeyde等人提出的SISR方法,文献[17]提出的SISR方法,本文提出方法和原始图像 Fig. 5 Results comparison of different methods (when s=2), from left to right: bicubic interpolation, the SISR method proposed by Zeyde, SISR method in [17], the method proposed in this paper and the original HR image |
此外, 为了定量比较本文方法与其他几种方法的好坏,采用下式来计算重构图像
| $ \begin{array}{l} {\rm{PSNR}}\left( {\hat y} \right) = 20{\log _{10}}\left( {255/{\rm{MSE}}\left( {\hat y} \right)} \right), \\ {\rm{MSE}}\left( {\hat y} \right) = \sqrt {\frac{{{{\left( {{y_{\rm{h}}}-\hat y} \right)}^2}}}{{M \times N}}} 。\end{array} $ |
其中,M×N为重构图像中像素的个数。图 3所示的测试图像集根据上式计算所得的PSNR值如表 1所示。
|
|
表 1 s=2和s=3时,几种方法的PSNR值对比 Tab. 1 The contrast of the PSNR results using different SR methods when s=2 and s=3 |
从实验结果可以看出, 当s=2或3时, 采用本文提出的SISR方法得到的重构图像的PSNR值均优于Zeyde等人提出的SISR算法、自举算法[1]以及文献[17]提出的方法, 证明了本文方法的正确性和有效性。
4 结语本文提出的SISR方法结合了Zeyde等人提出的LR图像自举算法以及双重稀疏性字典的训练方法, 是针对文献[17]提出方法的改进。在训练阶段,采用的训练样本数据源取自差值图像的小波变换域, 因而具有双重稀疏性字典的优点。实验证明,本文提出的SISR方法, 能够通过恢复出各个小波系数图像中的细节信息, 来获得更好的重构效果。同时, 由于本文的SISR方法结合了LR图像的自举算法, 在对训练样本图像进行学习的同时, 对输入待处理LR图像自身所包含的信息也进行了学习, 这使得该方法对于不同类型的测试图像将具有更好的适应性。如何将图像的卡通、纹理分解嵌入到本文提出的SISR方法中, 以及如何对字典训练迭代算法进行优化, 是之后值得研究的课题。
| [1] |
ELAD M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing[M]. Heidelberg: Springer, 2010: 341-343.
|
| [2] |
HOU H S, ANDREWS H C. Cubic spline for image interpolation and digital filtering[J]. IEEE Transaction on Acoustics, Speech and Signal Processing, 1978, 26(6): 508-517. DOI:10.1109/TASSP.1978.1163154 |
| [3] |
DAI S, HAN M, XU W, et al. Soft edge smoothness prior for alpha channel super resolution[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2007: 1-8.
|
| [4] |
ZHANG L, WU X L. An edge-guided image interpolation algorithm via directional filtering and data fusion[J]. IEEE Transaction on Image Processing, 2006, 15(8): 2226-2238. DOI:10.1109/TIP.2006.877407 |
| [5] |
FREEMAN W T, PASZTOR E C, CARMICHAEL O T. Learning low-level vision[J]. International Journal of Computer Vision, 2000, 40(1): 25-47. |
| [6] |
FREEMAN W T, JONES T R, PASZTOR E C. Example-based super-resolution[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 56-65. DOI:10.1109/38.988747 |
| [7] |
WANG Q, TANG X, SHUM H. Patch based blind image super resolution[C]//Tenth IEEE International Conference on Computer Vision. IEEE, 2005: 709-716.
|
| [8] |
CHANG H, YEUNG D, XIONG Y M. Super-resolution through neighbor embedding[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2004: 275-282.
|
| [9] |
YANG J C, WANG Z W, LIN Z, et al. Coupled dictionary learning for image super-resolution[J]. IEEE Transactions on Image Processing, 2012, 21(8): 3467-3478. DOI:10.1109/TIP.2012.2192127 |
| [10] |
YANG J C, WRIGHT J, HUANG T, et al. Image super-resolution as sparse representation of raw image patches[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2008, 1-8.
|
| [11] |
YANG J C, WRIGHT J, HUANG T, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873. DOI:10.1109/TIP.2010.2050625 |
| [12] |
ZEYDE R, ELAD M, PROTTER M. On single image scale-up using sparse representations[C]//International Conference on Curves and Surfaces. Springer-Verlag, 2010: 711-730.
|
| [13] |
AI N, PENG J Y, ZHU X, et al. SISR via trained double sparsity dictionaries[J]. Multimedia Tools and Applications, 2015, 74(6): 1997-2007. DOI:10.1007/s11042-013-1736-x |
| [14] |
SUETAKE N, SAKANO M, UCHINO E. Image super-resolution based on local self-similarity[J]. Optical Review, 2008, 15(1): 26-30. |
| [15] |
GLASNER D, BAGON S, IRANI M. Super-resolution from a single image[C]//International Conference on Computer Vision. IEEE, 2009: 349-356.
|
| [16] |
ZHU Z L, GUO F D, YU H, et al. Fast single image super-resolution via self-example learning and sparse representation[J]. IEEE Transaction on Multimedia, 2014, 16(8): 2178-2190. DOI:10.1109/TMM.2014.2364976 |
| [17] |
AI N, PENG J Y, ZHU X, et al. Single image super-resolution by combining self-learning and example-based learning methods[J]. Multimedia Tools and Applications, 2016, 75(11): 6647-6662. DOI:10.1007/s11042-015-2597-2 |
| [18] |
AHARON M, ELAD M, BRUCKSTEIN A M. The K-SVD: An algorithm for designing of over-complete dictionaries for sparse representation[J]. IEEE Transaction on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [19] |
OPHIR B, LUSTIG M, ELAD M. Multi-scale dictionary learning using wavelets[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 1014-1024. DOI:10.1109/JSTSP.2011.2155032 |
 2018, Vol. 48
2018, Vol. 48