2. 陕西省能源化工研究院, 陕西 西安 710069;
3. 陕西延长石油(集团)有限责任公司研究院, 陕西 西安 710075
2. Shaanxi Provincial Institute of Energy Resources & Chemical Engineering, Xi′an 710069, China;
3. Research Institute of Shaanxi Yanchang Petroleum (Group) Co. Ltd., Xi′an 710075, China
近年来, CO2驱油技术成为低渗透储层提高采收率的热点技术,低渗储层CO2驱油相对渗透率的研究也被纳入重点研究内容。鄂尔多斯盆地陕北地区延长组的致密砂岩油藏作为中国低渗透油藏的典型代表,学者对其开展了大量CO2驱油相关技术的研究和矿场实践探索[1-3]。然而遗憾的是, 目前尚无合适的相渗模型能真实反映该区CO2驱油的渗流特征。已实施CO2驱油试验的油区,虽进行过相渗测试, 但其数据处理仍沿用常规岩心的处理方法。以期用传统的“JBN”法获得的“拟相对渗透率曲线”代替真实低渗透储层CO2驱相渗曲线, 不具有针对性和适用性, 不能真实反映该区储层CO2驱相渗特征, 对科研及生产产生了误导。在此背景下,本研究立足于低渗透砂岩储层的非线性渗流规律, 全面考虑CO2驱油过程中溶解降黏、气相滑脱等影响因素, 建立低渗透砂岩油藏CO2非混相驱相渗计算模型, 以期更加真实地揭示陕北地区致密砂岩储层CO2驱相渗特征,以提高油藏工程及数值模拟等研究的可靠性。
1 非线性渗流规律与数学描述CO2注入低渗透储层后, 由于低渗透储层的复杂孔喉特征、流体的非牛顿流变学特征以及流体/骨架间的相互作用等内在因素, 导致流体在低渗透砂岩储层中产生非线性渗流[4-8]。
不同学者先后通过不同的数学模型对低速非线性渗流进行了描述, 且呈现了形式由简单到复杂、参数由少到多、精度由低到高的发展历程(见表 1)。拟启动压力模型认为,低于拟启动压力梯度时流体不流动, 同时将高于拟启动压力梯度的低速非线性流简化为通过拟启动压力梯度表征的线性流, 形式过于简单, 得出的分析结果与生产实际相差甚远。直线逼近、二次函数逼近、幂函数逼近等分段模型, 通过不同的函数形式拟合非线性段, 得到了较启动压力模型更接近实际情况的分析结果, 但这种分段模型需要确定线性与非线性渗流的临界点, 增加了应用的难度[9]。邓英尔等[10]、杨清立等[11]、姜瑞忠等[12]提出的连续函数模型, 通过一个连续方程分析低渗储层介质非线性渗流规律, 解决了分段模型需要确定临界点的问题。但是,这些模型中包含的参数并不能直接来源于实验, 需要通过庞大的计算过程得出, 且无明确的物理意义。黄延章等[13]提出的三参数连续模型,将最小启动压力梯度(λa)、拟启动压力梯度(λb)、线性段斜率(
|
|
表 1 常见的非线性渗流模型 Tab. 1 Common nonlinear seepage flow model |
基于黄延章等[13]提出的三参数非线性渗流方程, 考虑CO2非混相驱过程中的气相滑脱、CO2在原油中的溶解及溶解后流体黏度的变化等, 综合Buckley-Leverett[14-15]驱油机理, 建立低渗透砂岩油藏CO2非混相驱非稳态测算相渗曲线的计算模型。
2.1 不混溶气驱相渗模型的建立 2.1.1 运动方程根据三参数非线性渗流的规律, 为简化计算, 油、气相的非线性运动方程改写为:
| $ \begin{array}{l} - \frac{{\partial {p_{\rm{o}}}}}{{\partial x}} = \frac{{{Q_{\rm{o}}}{\mu _{\rm{o}}}}}{{AK{K_{r{\rm{o}}}}\left[ {1 - \frac{{{\lambda _{b{\rm{o}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{o}}}} - {\lambda _{a{\rm{o}}}}} \right)}}} \right]}} = \\ \frac{{u{f_{\rm{o}}}{\mu _{\rm{o}}}}}{{K{K_{r{\rm{o}}}}\left[ {1 - \frac{{{\lambda _{b{\rm{o}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{o}}}} - {\lambda _{a{\rm{o}}}}} \right)}}} \right]}}, \end{array} $ | (1) |
| $ \begin{array}{l} - \frac{{\partial {p_{\rm{g}}}}}{{\partial x}} = \frac{{{Q_{\rm{g}}}{\mu _{\rm{g}}}}}{{AK{K_{r{\rm{g}}}}\left[ {1 - \frac{{{\lambda _{b{\rm{g}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{g}}}} - {\lambda _{a{\rm{g}}}}} \right)}}} \right]}} = \\ \frac{{u{f_{\rm{g}}}{\mu _{\rm{g}}}}}{{K{K_{r{\rm{g}}}}\left[ {1 - \frac{{{\lambda _{b{\rm{g}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{g}}}} - {\lambda _{a{\rm{g}}}}} \right)}}} \right]}}。\end{array} $ | (2) |
式中:P为压力, MPa; x为沿驱替方向的流动距离, m; μ为流体黏度, mPa·s; Q为流量, cm3/s; u为流速, cm/s; A为岩心截面积, cm2; f为流体分流量, 无因次; |▽P|为岩心两端的压力梯度, MPa/m; K为绝对渗透率, ×10-3μm2; Kr为相对渗透率, 无因次; λa,λb分别为启动压力梯度和拟启动压力梯度, MPa/m; 下标o,g分别代表油相、气相。
2.1.2 等饱和度面移动方程根据Buckley-Leverett驱油机理, CO2驱油岩样沿程等饱和度面移动方程为
| $ x = \frac{{{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right)}}{{\varphi A}}\int_0^t {Q\left( t \right){\rm{d}}t} , $ | (3) |
出口端L处为
| $ L = \frac{{{{f'}_{\rm{g}}}\left( {{S_{{\rm{g}}e}}} \right)}}{{\varphi A}}\int_0^t {Q\left( t \right){\rm{d}}t} , $ | (4) |
| $ \frac{x}{L} = \frac{{{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right)}}{{{{f'}_{\rm{g}}}\left( {{S_{{\rm{g}}e}}} \right)}}。$ | (5) |
引入无因次注气量V(t),并代入L表达式:
| $ \bar V\left( t \right) = \frac{{\int_0^t {Q\left( t \right){\rm{d}}t} }}{{\varphi AL}} = \frac{1}{{{{f'}_{\rm{g}}}\left( {{S_{{\rm{g}}e}}} \right)}}。$ | (6) |
式中: Sg为含气饱和度; Sge为岩心出口端含气饱和度; fg′ (Sg)为气相分流量对含气饱和度的导数; fg′ (Sge)为气相在岩心出口端的分流量对含气饱和度的导数; φ为岩样孔隙度。
2.1.3 油相相对渗透率根据运动方程得岩心两端压差Δp为:
| $ \begin{array}{l} \Delta p = {p_1} - {p_2} = - \int_0^L {\frac{{\partial p}}{{\partial x}}{\rm{d}}x} = \\ \frac{{u{\mu _o}}}{K}\int_0^L {\frac{{{f_o}}}{{{K_{r{\rm{o}}}}\left[ {1 - \frac{{{\lambda _b}}}{{\left( {\left| {\nabla P} \right| + {\lambda _b} - {\lambda _a}} \right)}}} \right]}}{\rm{d}}x} 。\end{array} $ | (7) |
根据等饱和度面移动方程有:
| $ {\rm{d}}x = \frac{L}{{{{f'}_{\rm{g}}}\left( {{S_{{\rm{g}}e}}} \right)}}{\rm{d}}{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right). $ | (8) |
将dx,V(t)带入Δp中得:
| $ \begin{array}{l} \Delta p = \frac{{u{\mu _o}}}{K}\frac{L}{{{{f'}_{\rm{g}}}\left( {{S_{{\rm{g}}e}}} \right)}},\\ \int_0^{{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right)} {\frac{{{f_{\rm{o}}}}}{{{K_{r{\rm{o}}}}\left[ {1 - \frac{{{\lambda _b}}}{{\left( {\left| {\nabla P} \right| + {\lambda _b} - {\lambda _a}} \right)}}} \right]}}{\rm{d}}{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right)} , \end{array} $ | (9) |
整理得:
| $ \begin{array}{l} \int_0^{{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right)} {\frac{{{f_{\rm{o}}}}}{{{K_{r{\rm{o}}}}\left[ {1 - \frac{{{\lambda _b}}}{{\left( {\left| {\nabla P} \right| + {\lambda _b} - {\lambda _a}} \right)}}} \right]}}{\rm{d}}{{f'}_{\rm{g}}}\left( {{S_{\rm{g}}}} \right)} = \\ \;\;\;\;\;\frac{{\Delta pK}}{{u{\mu _{\rm{o}}}L\bar V\left( t \right)}} = \frac{1}{{\bar V\left( t \right)I}} \end{array} $ | (10) |
其中I为注入能力比,
公式(10)两边对fg′ (Sg)求导并整理得
| $ \begin{array}{l} {K_{r{\rm{o}}}}\left( {{S_{{\rm{g}}e}}} \right) = \\ \frac{{{f_{\rm{o}}}\left( {{S_{{\rm{g}}e}}} \right)}}{{\left[ {1 - \frac{{{\lambda _b}}}{{\left( {\left| {\nabla P} \right| + {\lambda _b} - {\lambda _a}} \right)}}} \right]}}\frac{{{\rm{d}}\left[ {\frac{1}{{\bar V\left( t \right)}}} \right]}}{{{\rm{d}}\left[ {\frac{1}{{\bar V\left( t \right)I}}} \right]}}。\end{array} $ | (11) |
由非线性渗流方程得岩心出口端气、油流量比为
| $ \begin{array}{l} \frac{{{Q_{\rm{g}}}}}{{{Q_{\rm{o}}}}}\frac{{{K_{r{\rm{g}}}}/{\mu _{\rm{g}}}}}{{{K_{r{\rm{o}}}}/{\mu _{\rm{o}}}}}\frac{{1 - \frac{{{\lambda _{b{\rm{g}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{g}}}} - {\lambda _{a{\rm{g}}}}} \right)}}}}{{1 - \frac{{{\lambda _{b{\rm{o}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{o}}}} - {\lambda _{a{\rm{o}}}}} \right)}}}} = \\ \frac{{Q{f_{\rm{g}}}}}{{Q{f_{\rm{o}}}}} = \frac{{1 - {f_{\rm{o}}}}}{{{f_{\rm{o}}}}}。\end{array} $ | (12) |
因此, 气相相对渗透率为
| $ \begin{array}{l} {K_{r{\rm{g}}}} = \frac{{1 - {f_{\rm{o}}}}}{{{f_{\rm{o}}}}}\frac{{{K_{r{\rm{o}}}}\left( {{S_{{\rm{g}}e}}} \right){\mu _{\rm{g}}}}}{{{\mu _{\rm{o}}}}} \times \\ \;\;\;\;\;\;\;\;\;\frac{{1 - \frac{{{\lambda _{b{\rm{o}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{o}}}} - {\lambda _{a{\rm{o}}}}} \right)}}}}{{1 - \frac{{{\lambda _{b{\rm{g}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{g}}}} - {\lambda _{a{\rm{g}}}}} \right)}}}}。\end{array} $ | (13) |
根据Buckley-Leverett驱油机理, 岩样出口端含气、含油饱和度方程为
| $ \begin{array}{l} {S_{{\rm{g}}e}} = \overline {{S_{\rm{g}}}} - \bar V\left( t \right) \cdot {f_{\rm{o}}}\left( {{S_{{\rm{g}}e}}} \right) = \\ \;\;\;\;\;\;\;\;{{\bar V}_{\rm{o}}}\left( t \right) - {f_{\rm{o}}}\left( {{S_{{\rm{g}}e}}} \right)\bar V\left( t \right),\\ {S_{\rm{o}}} = 1 - {S_{wc}} - {S_{{\rm{g}}e}}。\end{array} $ | (14) |
方程(11),(13),(14)构成了满足非线性渗流规律的不混溶气驱相对渗透率的计算模型。
2.2 考虑溶解及滑脱效应的相渗模型上述相对渗透率计算模型是建立在注入气体与油相不混溶的基础之上的。实际中, 要真实准确地描述CO2驱各相相对渗透率, 必须考虑CO2在原油中的溶解、降黏及气相滑脱效应等因素的影响。
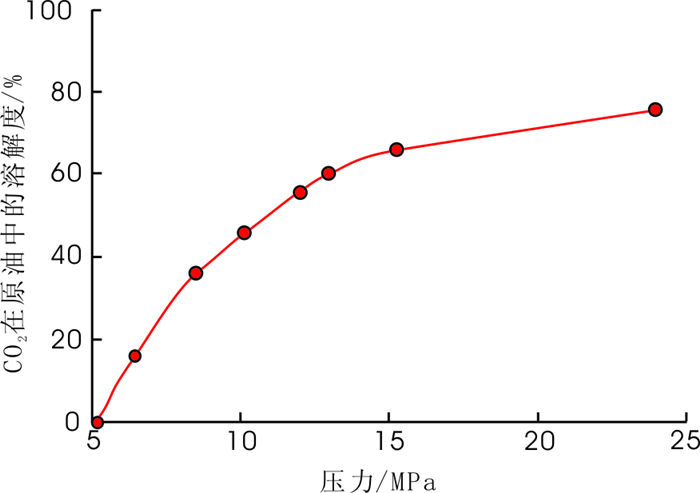
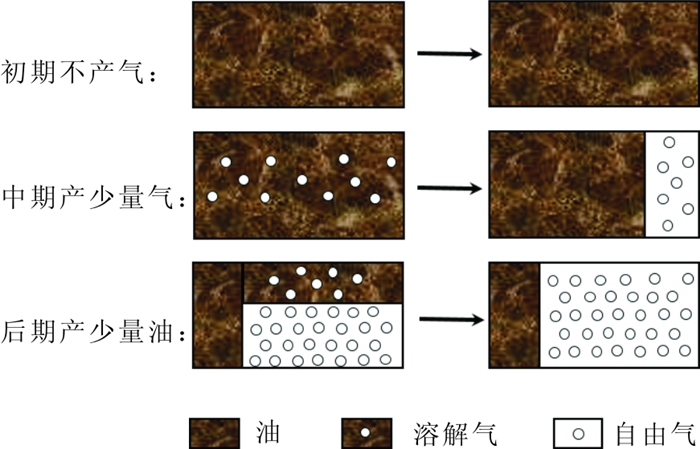
2.2.1 CO2溶解作用CO2在原油中有极强的溶解性。根据陕北某致密砂岩油藏油样溶胀实验的结果, CO2在地层条件下的溶解度达到60%(见图 1)。油气两相在地层中渗流时流体存在的状态有:油、束缚水、自由气、溶解气。而气相的状态取决于地层条件及其在油相中的溶解度大小。不同生产阶段的产出流体在地层压力Pf至计量器压力Pa条件下的状态如图 2所示。
|
图 1 CO2溶解度变化曲线(地层温度下) Fig. 1 CO2 solubility curve |
|
图 2 各阶段产出流体的状态 Fig. 2 Production fluid state at each stage |
1) 初期不产气阶段:CO2尚未突破, 产出物仅为油。
2) 中期产少量气阶段:CO2为分散相, 计量器中产气少而产油多, 在地层条件下CO2以溶解气形式存在, 且地层压力下的产油量需经CO2的溶解度αo和原油的体积膨胀系数βo进行矫正。
3) 后期产少量油阶段:CO2突破后呈连续相分布, 地层条件下CO2主要以自由气形式存在, 同时少量的气体溶于原油。此时产气量需通过地层平均压力进行矫正, 而地层压力下的产油量需经体积膨胀系数βo进行矫正[16]。
3个生产阶段的产出物在地层压力下的产量矫正为:
| $ \begin{array}{l} {Q_{{\rm{g}}f}} = \left\{ \begin{array}{l} 0,{Q_{{\rm{g}}s}} = 0\\ 0,0 < {Q_{{\rm{g}}s}} < {\alpha _{\rm{o}}} \cdot {Q_{{\rm{o}}s}}\\ \frac{{2{p_a}}}{{\Delta p + 2{p_a}}}\left( {{Q_{{\rm{g}}s}} - {\alpha _{\rm{o}}} \cdot {Q_{{\rm{o}}s}}} \right),{Q_{{\rm{g}}s}} \ge {\alpha _{\rm{o}}} \cdot {Q_{{\rm{o}}s}} \end{array} \right.,\\ {Q_{{\rm{o}}f}} = \\ \left\{ \begin{array}{l} {Q_{{\rm{o}}s}},{Q_{{\rm{g}}s}} = 0\\ \frac{{{Q_{{\rm{g}}s}}}}{{{\alpha _{\rm{o}}}}} \cdot {\beta _{\rm{o}}} + \left( {{Q_{{\rm{o}}s}} - \frac{{{Q_{{\rm{g}}s}}}}{{{\alpha _{\rm{o}}}}}} \right),0 < {Q_{{\rm{g}}s}} < {\alpha _{\rm{o}}} \cdot {Q_{{\rm{o}}s}}\\ {Q_{{\rm{o}}s}} \cdot {\beta _{\rm{o}}},{Q_{{\rm{g}}s}} \ge {\alpha _{\rm{o}}} \cdot {Q_{{\rm{o}}s}} \end{array} \right.。\end{array} $ | (15) |
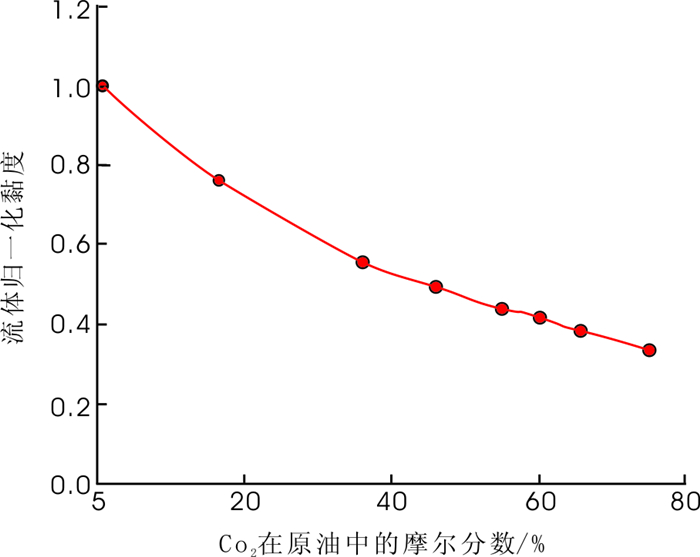
CO2溶于原油后可以有效降低原油黏度, 这是CO2提高采收率的重要原理之一。图 3中反映CO2对陕北地区某致密砂岩油藏原油的降黏幅度达到60%。因此, CO2驱油相对渗透率测算过程中, 流体黏度的变化是必须要考虑的因素。
|
图 3 CO2对原油的溶解降粘曲线 Fig. 3 Oil viscosity curve for the dissolution of CO2 |
CO2对原油的降黏作用是通过CO2气体与原油组分间的相互作用实现的。组分模型计算原油/CO2混合体系黏度需要的参数多, 且较为繁琐, 而经典的Arrhenius方程[17]可以满足一般混合物黏度计算精度的需要。因此,计算过程中采用该方程计算流体黏度。其计算公式为
| $ {\mu _{{\rm{mix}}}} = \mu _1^{{x_1}} \cdot \mu _2^{{x_2}}, $ | (16) |
式中:μmix为混合物黏度, mPa·s; x1,x2为不同相所占的比例; μ1x1,μ2x2为各相流体黏度, mPa·s。
2.2.3 气相滑脱作用罗瑞兰等[18]指出,当储层渗透率低于1×10-3μm2时, 滑脱效应对气藏产量有明显影响, 且影响程度由渗透率和压力共同决定:渗透率越低, 气藏压力越低, 滑脱效应越显著。因此, 在低渗透储层气相渗流过程中, 滑脱效应是不可忽视的因素。
Klinkenberg[19]最先提出气体滑脱效应, 并给出考虑滑脱因子和平均压力的气测渗透率表达式:
| $ {K_{\rm{g}}} = K\left( {1 + \frac{b}{p}} \right)。$ | (17) |
气体滑脱因子b与分子平均自由程及毛管半径有关。为了更好地进行工程应用, Sampath等[20]回归实验数据, 提出滑脱因子与孔隙度和渗透率存在以下关系式:
| $ b = 0.0955{\left( {\frac{k}{\varphi }} \right)^{ - 0.53}}。$ | (18) |
应用该计算方法, 对上述气相相对渗透率计算模型进行修正得到:
| $ \begin{array}{l} {K_{r{\rm{g}}}} = \frac{{1 - {f_{\rm{o}}}}}{{{f_{\rm{o}}}}}\frac{{{K_{r{\rm{o}}}}\left( {{S_{{\rm{g}}e}}} \right){\mu _{\rm{g}}}}}{{{\mu _{\rm{o}}}}} \times \\ \frac{{1 - \frac{{{\lambda _{b{\rm{o}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{o}}}} - {\lambda _{a{\rm{o}}}}} \right)}}}}{{1 - \frac{{{\lambda _{b{\rm{g}}}}}}{{\left( {\left| {\nabla P} \right| + {\lambda _{b{\rm{g}}}} - {\lambda _{a{\rm{g}}}}} \right)}}}}\frac{1}{{1 + \frac{b}{{\bar p}}}}。\end{array} $ | (19) |
式(11),(14),(15),(16),(19)即构成了低渗透砂岩油藏CO2非混相驱过程中相对渗透率计算模型。
3 实例计算分析 3.1 非稳态CO2非混相驱实验描述实验样品主要包括岩心、地层水、原油及CO2。岩样源自陕北地区致密砂岩油藏某油区的天然岩心。实验用地层水、原油均为按实际地层样品组成配置的模拟流体。CO2纯度99.9%。样品详细参数见表 2~4。
|
|
表 2 地层水组成 Tab. 2 Compositional analysis result of the reservoir brine |
|
|
表 3 油样物性参数表 Tab. 3 Physical property parameter of the oil sample |
|
|
表 4 岩心参数表 Tab. 4 Physical property parameter of the core |
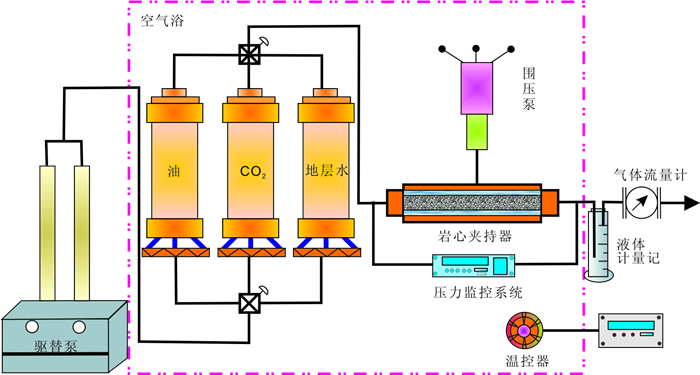
实验装置主要包括动力泵、中间容器、岩心夹持器、压力监控器、流体计量装置等。实验流程图见图 4。
|
图 4 CO2驱实验流程图 Fig. 4 Schematic diagram of CO2 displacement experiment |
实验步骤据行业标准《SY/T5345-2007油水相对渗透率测定方法—非稳态法》执行, 具体包括:①依据地层流体组成对实验流体进行配置; ②岩样洗油、烘干, 几何尺寸及气测渗透率测量; ③抽真空, 饱和地层水并测算孔隙度; ④已饱和地层水的岩样置入驱替装置, 空气浴采用梯度升温的方式升至地层温度60℃, 并恒温24小时; ⑤定流速0.8 cm3/min油驱水, 饱和油, 建立束缚水饱和度, 并保证围压始终比驱替压力高出2 MPa, 待出口流量稳定, 测定束缚水饱和度下的油相有效渗透率; ⑥定流速0.8 cm3/min CO2驱油, 并记录各个时刻的驱替压力、产油量及产气量; ⑦气驱至不产油, 测定残余油状态下的气相有效渗透率后结束实验。
3.2 相渗曲线计算及分析利用建立的模型对上述实验数据进行处理, 得到陕北地区致密砂岩油藏某油区基于非线性渗流的, 考虑CO2溶解、降黏、气相滑脱的CO2非混相驱油相渗曲线(见图 5)。结果整体上表现出以下特点:①低含气饱和度下, 油相相对渗透率随含气饱和度的增加快速下降, 而气相相对渗透率则缓慢上升; 高含气饱和度下, 气相相对渗透率快速上升。②气相相渗端点值较低, 不足0.1, 表明气体渗流能力相对较弱。③束缚水饱和度、残余油饱和度等特征值均较高, 分别为35%,30%, 说明CO2非混相驱替能力有限。④两相区范围窄, 约35%, 说明两相共渗能力和空间有限, 具有低黏、低渗油藏相对渗透率曲线的特征。
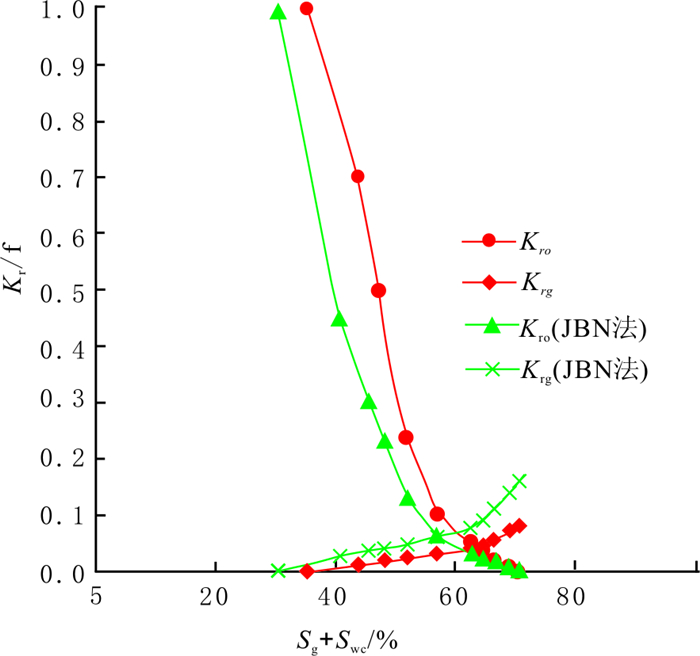
|
图 5 致密砂岩储层CO2非混相驱典型相渗曲线 Fig. 5 Typical relative permeability curve of immiscible CO2 flooding in tight sandstone reservoir |
与传统的“JBN”方法计算的相渗结果相比, 本模型计算结果表现出明显的差异(见图 5):油相相对渗透率有较大幅度的提高; 气相渗透率有较大幅度的降低; 束缚气饱和度有所降低。本模型所反映出的这种差异在油藏工程分析中起到了举足轻重的作用, 因此渗流模式、CO2在原油中的溶解降黏及气相滑脱效应是相渗测算中不可忽略的因素。
为分析渗流模式、CO2在原油中的溶解降黏及气相滑脱效应等因素对致密砂岩储层CO2非混相驱相渗的影响程度, 本研究进行单因素影响的相渗曲线计算, 结果如图 6~8所示。其中,图 7和图 8均基于非线性渗流模型进行计算。
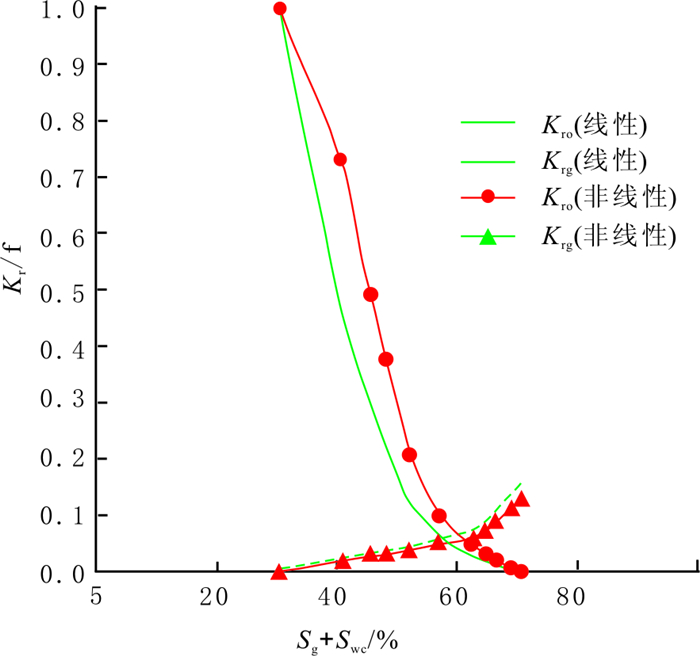
|
图 6 不同渗流模型计算的相渗曲线 Fig. 6 Relative permeability curves of different seepage models |
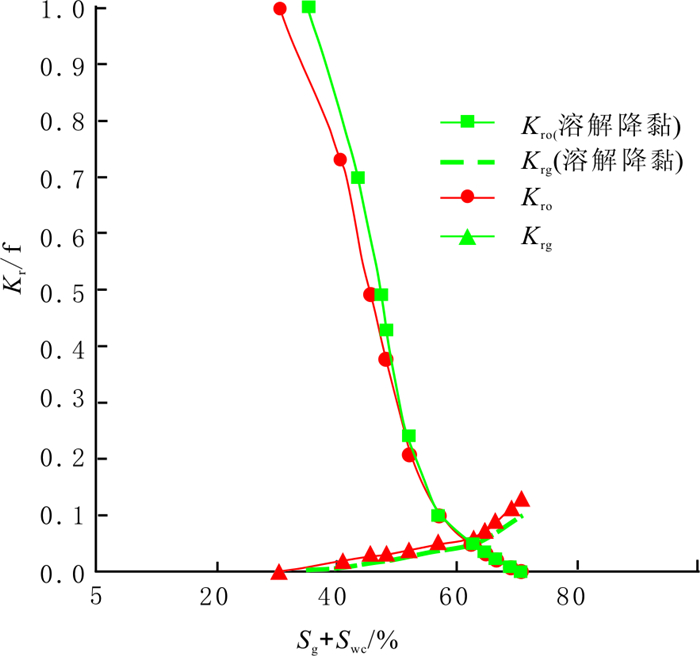
|
图 7 考虑溶解降粘作用的相渗曲线 Fig. 7 Relative permeability curve considering effect of dissolution and viscosity reduction |
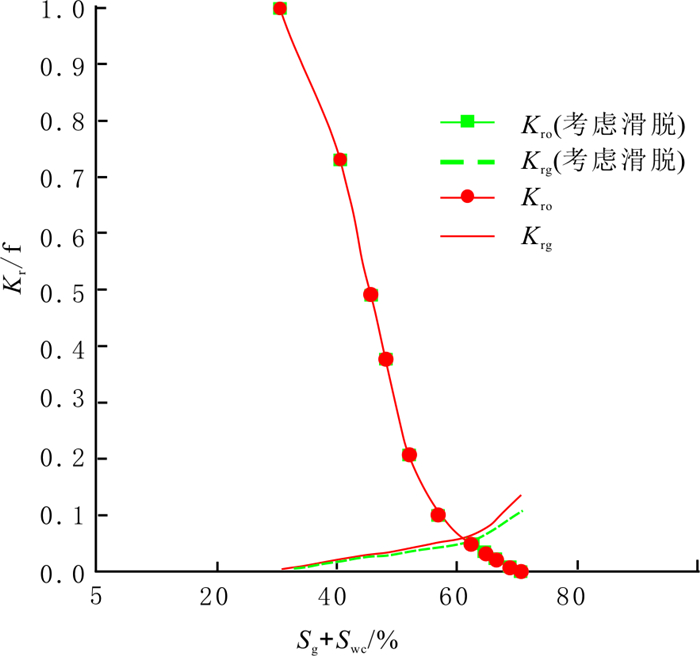
|
图 8 考虑CO2气体滑脱效应的相渗曲线 Fig. 8 Relative permeability curve considering effect of gas slippage |
相对于线性渗流模型, 基于三参数非线性渗流的致密砂岩油藏CO2驱油相渗曲线表现出较大的不同:油相相对渗透率上升, 而气相相对渗透率下降, 等渗点明显右移。如果运用线性渗流模型进行分析和预测, 会得出相对于非线性渗流较差的驱油效果。
由图 7可以看出, 考虑CO2气体在原油中的溶解降黏作用所计算的相渗曲线与忽略CO2的溶解作用相比有较大不同。由于忽略CO2气体的溶解, 气体均视为以自由气的形式产出, 致气相渗透率值偏高、油相渗透率值偏低。同时, 溶解了CO2气体的部分原油黏度降低, 流动能力增加, 也可引起油相相对渗透率增加。
从图 8可以看出, 考虑CO2气体的滑脱效应时, 油相渗透率基本不变, 气相相对渗透率有小幅度下降。CO2气体在致密多孔介质中的流动包括滑脱流和渗流, 未经滑脱效应矫正时, 滑脱产生的气体流量同时被记入渗流流量, 导致气相渗透率偏大。
4 结论1) 建立了低渗透砂岩油藏非稳态CO2非混相驱相渗计算模型。该模型以低渗透储层的三参数非线性渗流规律为基础, 同时考虑了CO2驱油过程中溶解、降黏、气相滑脱效应等因素的影响。与传统“JBN”方法计算的相渗结果相比, 本模型计算结果表现出了明显的差异。
2) 进行了非稳态CO2驱油相渗实验, 得到了陕北地区某致密砂岩油藏CO2非混相驱典型相渗曲线。计算并对比了渗流模式、CO2的溶解降黏作用以及CO2气体滑脱效应等单因素对相渗曲线的影响。结果表明, 非线性渗流及CO2的溶解降黏均引起油相相对渗透率上升, 气相相对渗透率下降。考虑气相滑脱时, 气相相对渗透率有小幅度下降, 油相相对渗透率基本无变化。
| [1] |
王道夫. 鄂尔多斯盆地低渗透油气田开发技术[M]. 北京: 石油工业出版社, 2003.
|
| [2] |
王道富, 付金华, 雷启鸿, 等. 鄂尔多斯盆地低渗透油气田勘探开发技术与展望[J]. 岩性油气藏, 2007, 19(3): 126-130. |
| [3] |
樊建明, 张庆洲, 霍明会, 等. 超低渗透油藏注CO2开发方式优选及室内实验研究[J]. 西安石油大学学报(自然科学版), 2015, 30(5): 37-42. |
| [4] |
HE W, YANG L, MA C, et al. Effect of micro-pore structure parameter on seepage characteristics in ultra-low permeability reservoir: A case from chang6 reservoir of Ordos basin[J]. Natural Gas Geoscience, 2011, 22(3): 477-476. |
| [5] |
WANG R, LV X, GUO D. Feature parameters of micro pore throat in deep section high pressure and low-permeability sandstone reservoir[J]. Journal of China University of Mining & Technology, 2012, 41(1): 64-68. |
| [6] |
YUN M. Fractal study on seepage properties of non-Newtonian Sisko fluid flowing through porous media[J]. Journal of Huazhong Normal University (Natural Sciences), 2013, 47(4): 487-490. |
| [7] |
ZHANG S, SUN Y, WU X, et al. A comprehensive analysis of the seepage characters of non-Newtonian fluids in fractal porous media[J]. Journal of Porous Media, 2014, 17(12): 1031-1044. DOI:10.1615/JPorMedia.v17.i12 |
| [8] |
郑祥克, 陶永建, 门承全, 等. 低速非达西渗流产能方程的建立[J]. 新疆石油地质, 2003, 24(2): 158-160. |
| [9] |
黄延章. 低渗透油层渗流机理[M]. 北京: 石油工业出版社, 1999.
|
| [10] |
邓英尔, 刘慈群. 低渗油藏非线性渗流规律数学模型及其应用[J]. 石油学报, 2001, 22(4): 72-77. DOI:10.7623/syxb200104014 |
| [11] |
杨清立, 杨正明, 王一飞, 等. 特低渗透油藏渗流理论研究[J]. 钻采工艺, 2007, 30(6): 52-54. |
| [12] |
姜瑞忠, 杨仁峰. 低渗透油藏非线性渗流理论与数值模拟技术[M]. 北京: 石油工业出版社, 2010.
|
| [13] |
黄延章, 杨正明, 何英, 等. 低渗透多孔介质中的非线性渗流理论[J]. 力学与实践, 2013, 35(5): 1-8. DOI:10.6052/1000-0879-13-165 |
| [14] |
BUCKLEY S E, LEVERETT M C. Mechanism of fluid displacement in sands[J]. Transactions of the Aime, 1946, 146(1): 107-116. |
| [15] |
杨胜来, 魏俊之. 油层物理学[M]. 北京: 石油工业出版社, 2015.
|
| [16] |
董驰. CO2驱相对渗透率测试方法研究[D]. 大庆: 东北石油大学, 2011.
|
| [17] |
BLOOMFIELD V A, DEWAN R K. Viscosity of liquid mixtures[J]. Journal of Physical Chemistry, 1971, 75(20): 3113-3119. DOI:10.1021/j100689a014 |
| [18] |
罗瑞兰, 程林松, 朱华银, 等. 研究低渗气藏气体滑脱效应需注意的问题[J]. 天然气工业, 2007, 27(4): 92-94. |
| [19] |
KLINKENBERG L J. The permeability of porous media to liquids and gases[J]. Socar Proceedings, 1941, 2(2): 200-213. |
| [20] |
SAMPATH K, KEIGHIM C W. Factors affecting gas slippage in tight sandstones of cretaceous age in the Uinta basin[J]. Journal of Petroleum Technology, 1982, 34(11): 2715-2720. DOI:10.2118/9872-PA |
 2018, Vol. 48
2018, Vol. 48