2. 西安交通大学 医学部,陕西 西安 710061
2. Health Science Center, Xi′an Jiaotong University, Xi′an 710061, China
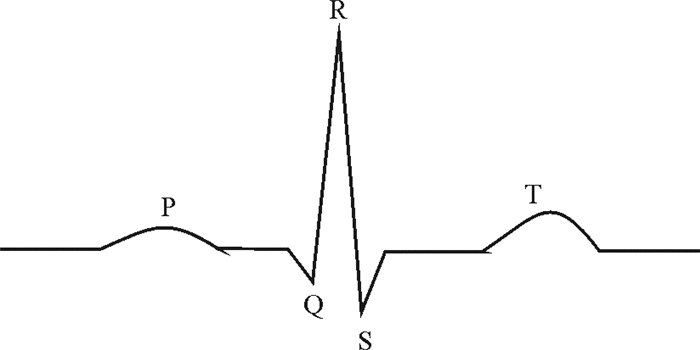
心电图(Electrocardiogram, ECG)是通过心电图仪从体表记录的能够反映心脏兴奋产生、传导和恢复过程中所产生的生物电位变化情况的曲线[1]。一次正常的心跳(即一个心动周期), 通常由P波、QRS波群和T波组成, 其持续时间大约为0.8s(如图 1所示)。最早出现的波形是由心房兴奋产生的P波(即反映心房除极过程), 通常表现为向上的圆钝平滑小波, 正常的持续时间为0.06s~0.12s;其次是由心室兴奋所产生的QRS波群, 为尖锐的上下波(即由向下的Q波, 向上的R波, 及紧跟的S波共同构成), 表示心室除极过程和心房复极过程的复合, 正常的持续时间为0.06s~0.1s;最后出现的是由心室兴奋恢复而产生的缓慢T波, 代表心室复极过程, 正常持续时间为0.1s~0.25s[2]。
|
图 1 一个正常的心动周期 Fig. 1 Anormal cardiac cycle |
R波具有较高的振幅和较大的斜率, 是ECG信号中最重要的组成部分, 蕴含着重要的生理病理信息。R波波峰(R峰)检测是心率变异性分析、心血管疾病诊断、生物识别和ECG编码系统的首要步骤。只有准确检测到R峰后, 才能正确定位出P波和T波, 进一步计算心率、RR间期、PR间期、ST段偏移等心电图特征, 从而完成心电图分析等工作。因此, 为了实现海量心电数据的实时判读, 开展心电信号R峰自动检测的研究具有极为重要的临床意义。
20世纪50年代起, R峰的自动检测技术逐渐兴起, 众多R峰自动检测方法被提出。这些方法大多基于差分运算[3]、数字滤波器[4-7]、经验模式分解(EMD)[8]、几何模板匹配[9]和神经网络[10]等。基于差分运算的检测算法, 主要利用R峰具有较大幅值和斜率的特点, 对去噪后的ECG信号进行差分运算并与设定的阈值进行比较, 从而确定R峰[13]。这类算法容易理解、操作简单、运算速度快, 但其抗噪性能较差从而导致R峰检测的准确率较低。基于几何模板匹配的检测算法, 主要利用相邻心动周期内心电信号具有较低差异性的特点, 对任意心动周期内的心电信号与QRS波群模板的相关性进行度量, 进而依据相关性大小筛选出待检QRS波群, 最终将振幅极大值确定为R峰[11]。该算法的局限性在于计算复杂、心电模板难以建立。基于数字滤波器的检测算法主要采用具有固定带宽的滤波器将非QRS波群频率占优带内心电信号成分滤除, 仅保留QRS波群频率占优带内的有效成分并结合决策规则完成R峰检测。该算法运行速度快, 但其检测性能与滤波器带宽的选择和集成器移动窗口的大小密切相关, 采用不同带宽的数字滤波器对同一心电信号进行R峰检测, 检测结果有显著差异。基于经验模式分解的检测算法, 能够将心电信号自适应地分解成若干个本征模态函数, 根据QRS波群的频率分布范围选择几个恰当的本征模态函数进行心电信号的重构, 进而在重构信号上进行模极值对的检测并将正模极值确定为R峰。该算法不需要对心电信号进行预处理, 很好地避免了参数选择问题, 但在含噪情况下选择恰当的本征模态函数(IMF)进行ECG重构极其困难且EMD分解十分耗时, 从而导致该类算法在临床中难以应用。
本文提出了一种新的基于小波变换的R峰自动检测方法。首先采用基于小波包分解的去基线漂移方法以及改进的小波阈值法对原始心电信号进行去噪处理; 继而, 对去噪后的心电信号进行小波变换, 在恰当的频率子带上检测出候选R峰, 并将其对应位置投影于心电信号; 最终, 根据候选R峰在心电信号上的位置信息进行精确筛选, 完成R峰检测。为了进一步说明所提R峰自动检测方法的有效性, 本文选用MIT-BIH心律失常数据库进行验证并采用错误检测率(DER)、真阳性率(+P)、敏感度(Se)、准确率(Acc)4个指标来评估该算法的性能。
1 小波变换与小波包分解 1.1 小波变换小波变换是一种进行信号分析的时间-尺度方法, 它具有多尺度分辨率分析的特点, 在时域和频域上同时具有表征信号局部特征的能力。通过伸缩和平移变换来实现心电信号在多个不同尺度上的细化, 将心电信号的时域及频域的局部特征同时反映在各个不同的频率带上, 突出心电信号的不同特征。小波变换可分为连续小波变换(Continuous wavelet transform, CWT)和离散小波变换(Discrete wavelet transform, DWT) [11-13]。
由于连续小波变换中的基函数具有较强的相关性, 会导致变换后得到的小波系数产生信息冗余, 从而影响信号分析的质量, 故本文仅采用离散小波变换对心电信号进行分析。给定母小波ψ(t), 采用尺度因子aj=2j和位移因子bj, k=2jk对ψ(t)进行伸缩和平移变换, 得到一组小波基函数序列
| $ {\psi _{{a_j},{b_{j,k}}}}\left( t \right) = {\left| {{a_j}} \right|^{ - \frac{1}{2}}}\psi \left( {\frac{{t - {b_{j,k}}}}{{{a_j}}}} \right)。$ |
在此基础上,信号S(t)的离散小波变换(DWT)定义为
| $ {\rm{DWT}}\left( {j,k} \right) = \int_{ - \infty }^\infty {S\left( t \right)\psi _{{a_j},{b_{j,k}}}^ * \left( t \right){\rm{d}}t} , $ |
其中ψ*aj, bj, k (t)为ψaj, bj, k(t)的复共轭。
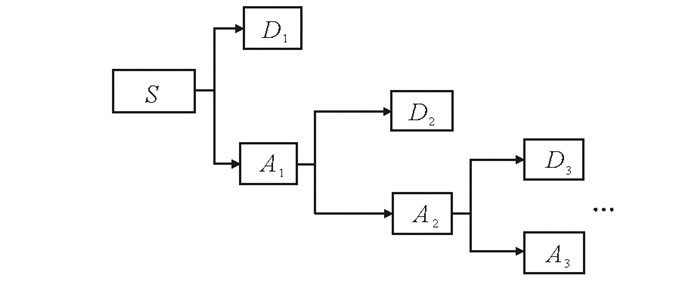
给定信号S, 其离散小波变换过程如图 2所示。设采样率为2L, 则由奈奎斯特采样定律可知, 第一层分解后可得L/2~L高频子带信号D1(细节部分)及0~L/2低频子带信号A1(近似部分), 其中D1由信号S经过高通滤波器滤波和二元下采样得到, A1由信号S经过低通滤波器滤波和二元下采样得到; 接下来, 对A1进行第二层分解, 可得L/22~L/2高频子带信号D2和0~L/22低频子带信号A2; 依次类推。
|
图 2 离散小波变换的示意图 Fig. 2 The diagram of discrete wavelet transformation |
小波包分解是一种能够很好地对信号进行时频局部化分析的信号处理方法。相比小波变换而言, 它能够同时对信号的低频以及高频成分进行表征, 为信号中未被细化的高频部分提供更精细的分解, 从而发掘高频部分蕴含的重要信息, 更加充分地对信号进行分析和研究。
给定一个信号S={s(1), s(2), …, s(n)}。令{H, G}为一对正交镜像滤波器, 其中H={hk}k∈Z为低通滤波器且G={gk}k∈Z为高通滤波器, 则S的小波包分解系数可表示为[11]
| $ \left\{ \begin{array}{l} {\omega _{2n}} = \sqrt 2 \sum\limits_{j \in {\bf{Z}}} {{h_j}{\omega _n}\left( {2t - j} \right)} \\ {\omega _{2n + 1}} = \sqrt 2 \sum\limits_{j \in {\bf{Z}}} {{g_j}{\omega _n}\left( {2t - j} \right)} \end{array} \right., $ | (1) |
其中
| $ \int_R {{\omega _0}\left( t \right){\rm{d}}t} = 1, $ |
| $ \sum\limits_{n \in Z} {{h_{n - 2k}}{h_{n - 2l}}} = {\delta _{k,l}}, $ |
| $ \sum\limits_{n \in Z} {{h_n}} = \sqrt 2 , $ |
| $ {g_k} = {\left( { - 1} \right)^k}{h_{1 - k}}。$ |
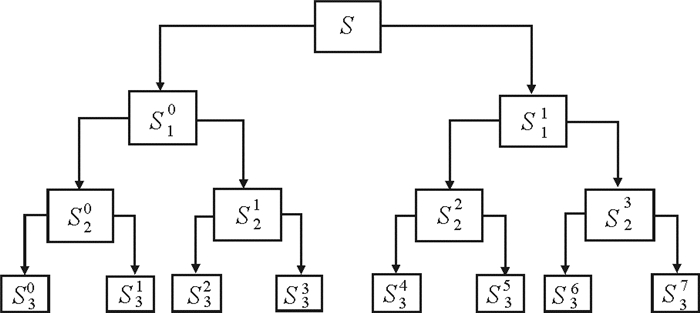
图 3为S的三层小波包分解示意图, 其中S10和S11分别为第一层分解后得到的低频信号与高频信号, 对应的小波包系数称为近似系数与细节系数; S20和S22为第二层分解后得到的低频信号, S21和S23为第二层分解后得到的高频信号; 以此类推。
|
图 3 小波包分解示意图 Fig. 3 The diagram of wavelet packet decomposition |
ECG信号在采集过程中会受到多种噪声的干扰, 主要包括基线漂移、工频干扰和肌电伪迹[2]。这些背景噪声的存在会大大降低R峰检测的可靠性。因此, 为了高效地实现R峰的自动检测, 需要对ECG信号进行去噪处理。本小节将介绍一种新的基于小波包分解与改进的小波阈值法相结合的心电信号去噪方法。
实际应用中最常用的去噪方法是由Donoho等人提出的软阈值去噪法[14], 其阈值函数为
| $ \begin{array}{l} {{\tilde \omega }_{j,k}} = \\ \left\{ \begin{array}{l} {\mathop{\rm sgn}} \left( {{\omega _{j,k}}} \right)\left( {\left| {{\omega _{j,k}}} \right| - \lambda } \right),\left| {{\omega _{j,k}}} \right| > \lambda \\ 0,\left| {{\omega _{j,k}}} \right| \le \lambda \end{array} \right. \end{array} $ | (2) |
其中ωj, k为小波系数, j为尺度因子, k为位移因子,
| $ \begin{array}{l} {{\tilde \omega }_{j,k}} = \\ \left\{ \begin{array}{l} {\mathop{\rm sgn}} \left( {{\omega _{j,k}}} \right)\left( {\left| {{\omega _{j,k}}} \right| - \frac{{\alpha \lambda }}{{1 + {{\rm{e}}^{1/\alpha \left( {\left| {{\omega _{j,k}}} \right| - \lambda } \right)}}}}} \right),\left| {{\omega _{j,k}}} \right| > \lambda \\ 0,\left| {{\omega _{j,k}}} \right| \le \lambda \end{array} \right., \end{array} $ | (3) |
其中
根据所定义的阈值函数(3), 本文提出一种新的心电信号噪方法(见算法1)。
算法1 (心电信号去噪方法) 给定原始心电信号S={s(1), s(2), …, s(n)}, 其中n表示信号长度。
步骤1 对原始心电信号S进行M层小波包分解, 得到一系列子带信号。将第M层所有子带信号记为SM0, SM1, …, SM2M-1, 其中SMi={sMi (1), …, sMi (m)}表示第i个分解节点上长度为m的信号, 其对应的小波包系数记为ωMi(i=0, 1, …, 2M-1);
步骤2 记包含在基线漂移频率分布范围内的子带信号集合为{SM0, SM1, …, SMk}, 找出能量比率(记为ρi)最大的子带信号SMi*:
| $ {i^ * } = \mathop {\arg \max }\limits_{0 \le i \le k} {\rho _i} = \mathop {\arg \max }\limits_{0 \le i \le k} \frac{{{E_i}}}{{\sum\limits_{i = 0}^k {{E_i}} }}, $ | (4) |
| $ {E_i} = \sum\limits_{l = 1}^m {{{\left( {s_M^i\left( l \right)} \right)}^2}} ,\;\;i = 0,1, \cdots ,k $ | (5) |
步骤3 更新所有分解子带信号SM0, SM1, …, SM2M-1所对应的小波包系数:
| $ {{\hat \omega }_{Mi}} = \left\{ \begin{array}{l} 0,\;\;i = {i^ * }\\ {{\tilde \omega }_{Mi}},\;\;i \ne {i^ * } \end{array} \right.\;\left( {i = 1,2, \cdots ,{2^M} - 1} \right), $ | (6) |
其中
步骤4 采用步骤3中的小波包系数对心电信号S进行重构, 得到去噪后的心电信号
本小节介绍一种新的基于小波变换的R峰自动检测方法。首先, 将去噪后的心电信号划分为若干等长的心电信号片段; 其次, 对每个心电信号片段进行离散小波变换, 并选择恰当的频率子带信号; 再次在该子带信号上采用自适应阈值法确定出候选R峰; 最后, 根据候选R峰在心电信号上的位置信息进行进一步筛选, 以完成最终的R峰检测。具体步骤见算法2。
算法2 (R峰自动检测方法)记
步骤1 将
步骤2 对Si进行离散小波变换(分解层数为N), 并根据心电信号的频率分布范围选择恰当的低频子带信号, 记为Aki={Aki (1), …, Aki (t)}(t < T), k∈{1, …, N}。
步骤3 在Aki上确定候选R峰位置。
1) 确定Aki上转折点所构成的集合TUR。
定义转折点Aki (j)满足如下条件:
| $ \left( {A_k^i\left( j \right) > A_k^i\left( {j - 1} \right)} \right) \wedge \left( {A_k^i\left( j \right) > A_k^i\left( {j + 1} \right)} \right) $ |
或
| $ \left( {A_k^i\left( j \right) < A_k^i\left( {j - 1} \right)} \right) \wedge \left( {A_k^i\left( j \right) < A_k^i\left( {j + 1} \right)} \right)。$ |
记TUR={Aki (1), Aki (2), …, Aki (l)}。
2) 确定动态阈值THR。
分别定义集合TUR的最小幅度平均值与最大幅度平均值为Min与Max, 其中Min为TUR中前m1个最小元素的平均值, Max为TUR中前m2个最大元素的平均值。令
| $ {\rm{THR}} = {d^ * }\left( {{\rm{Max}} - {\rm{Min}}} \right) $ | (7) |
为Aki 上的动态阈值, 其中参数d∈[0, 1]。
3) 确定候选R峰位置。
在TUR中选出大于动态阈值THR的所有点, 记为
| $ \overline {{\rm{TUR}}} = \left\{ {A_k^i\left( {{j_p}} \right)\left| {A_k^i\left( {{j_p}} \right) > {\rm{THR}}} \right.} \right\}_{p = 1}^{\bar l}。$ |
将TUR上所有点对应的位置序列记为
| $ r = \left\{ {r\left( 1 \right),r\left( 2 \right), \cdots ,r\left( {\bar l} \right)} \right\}, $ |
并称其为候选R峰位置序列。
步骤4 在Si上完成R峰的自动检测。
1) 采用小波变换逆变换将r映射到Si上, 得到Si上的候选R峰位置序列, 记为
| $ {R^i} = \left\{ {{R^i}\left( 1 \right),{R^i}\left( 2 \right), \cdots ,{R^i}\left( {\bar l} \right)} \right\}。$ |
2) 按照下列循环对Si上的候选R峰位置进行微调, 仍记为Ri:
| $ {\rm{For}}\;p = 1:\bar l $ |
① 对Ri(p)进行半径为v的加窗处理;
② 将Ri(p)更新为[Ri(p)-v, Ri(p)+v]上最大值所对应的位置。
End
3) 确定Si上最终的R峰位置。
首先, 计算Si上的RR间期序列
| $ {\rm{RR}} = \left\{ {{\rm{RR}}\left( 1 \right), \cdots ,R\left( {\bar l - 1} \right)} \right\}, $ |
其中RR(p)=Ri(p+1)-Ri(p), 1≤p≤l-1。
其次, 分别计算每一RR间期的左、右近邻平均值为:
| $ {M_{{\rm{left}}}}\left( p \right) = \frac{1}{5}\sum\limits_{j = p - 5}^{p - 1} {{\rm{RR}}\left( j \right)} , $ | (8) |
| $ {M_{{\rm{right}}}}\left( p \right) = \frac{1}{5}\sum\limits_{j = p - + }^{p + 5} {{\rm{RR}}\left( j \right)} 。$ | (9) |
最后, 按如下规则确定最终的R峰位置:若RR(p) < Mleft(p)且RR(p) < Mright(p), 则删除Ri(p); 否则, 保留Ri(p)。
将所有保留的R峰位置序列记为R={R1, R2, …, Rl*}, 其中l*为最终检测到的R峰个数。
3 数值实验结果及分析 3.1 心电数据集本文所使用的心电数据来自美国麻省理工大学和Beth Israel医院合作建立的MIT-BIH心律失常数据库[17]。该数据库一共包含48个时长约为30分钟的双导联心电记录, 采样率为360Hz, 分辨率为11bit, 且每个心电记录中均含有一种或多种心律失常心电。本文从中随机选取20个心电记录, 并采用每个记录中第一个导联的心电信号来验证所提R峰自动检测方法的有效性。文中所有实验均Matlar 8.5.0中运行。
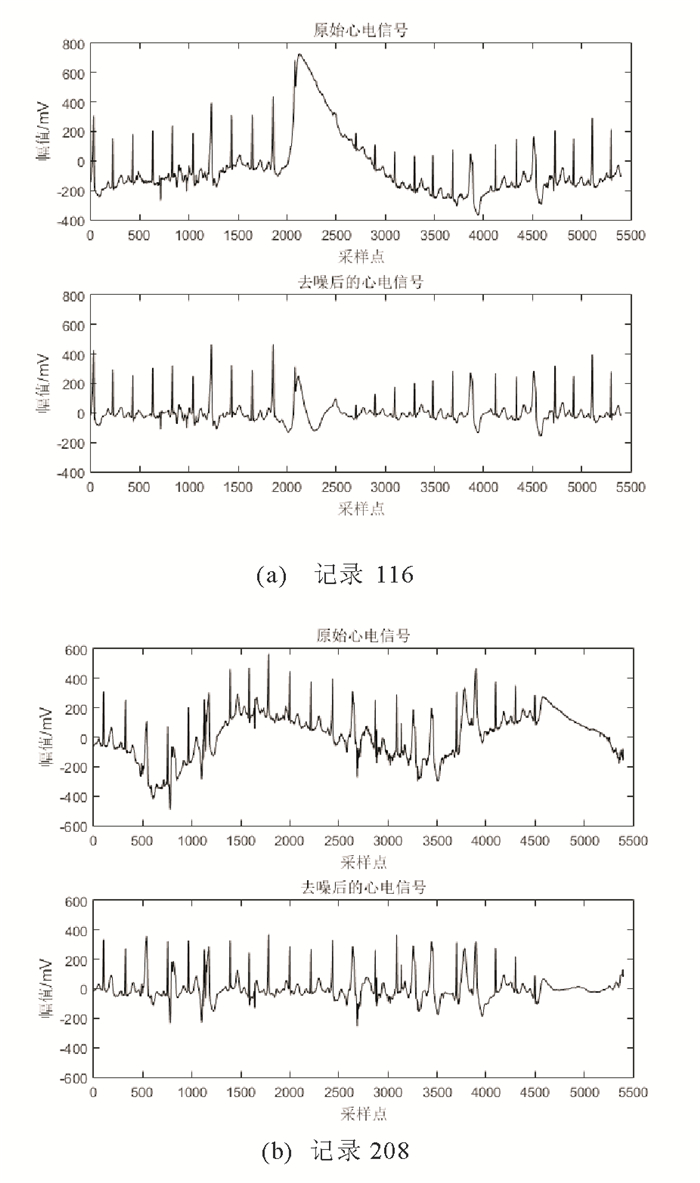
3.2 结果与分析在去噪过程中, 采用db6小波基函数对心电信号进行M=10层小波包分解。图 4展示了“记录116”与“记录208”两段原始心电信号及其去噪后的心电信号。从图中可以看出, 本文所提出的去噪方法有效去除了基线漂移及工频干扰等噪声。
|
图 4 心电信号的去噪效果 Fig. 4 Denoising performance for the ECG signal |
在R峰检测过程中, 取Q=180, 则分割后的每个心电片段长度为T=3 600。在DWT中, 采用db4小波基函数并取N=4。由于心电信号的能量主要集中在0~4Hz内, 故在低频子带信号A2上进行候选R峰的确定。根据QRS波群宽度的参考值为0.06s~0.12s, 实验中选取参数d=0.3, v=45。
本文采用敏感度Se、错误检测率DER、真阳性率+P和准确率Acc作为评估算法性能的度量指标, 分别表示如下[18]:
| $ {\rm{Se = }}\frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}} \times 100\% $ | (10) |
| $ {\rm{DER}} = \frac{{{\rm{FP}} + {\rm{FN}}}}{{{\rm{TP}}}} \times 100\% $ | (11) |
| $ + {\rm{P}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}} \times 100\% $ | (12) |
| $ {\rm{Acc}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}} + {\rm{FN}}}} \times 100\% $ | (13) |
其中TP(true positive, TP)表示正确检测真实R峰的个数; FP(false positive, FP)表示将非R峰判定为R峰的个数; FN(false negative, FN)表示漏检真实R峰的个数。
表 1为本文所提R峰自动检测方法应用于20个心电信号的数值实验结果。从表 1可看出本文所提方法的真阳性率、敏感度和准确率的均值分别达到99.67%,99.95%,99.62%。除心电记录104,111,116,208和232外, 其余检测准确率均在99.77%以上。
|
|
表 1 R峰检测方法的性能评估 Tab. 1 Performanceof the proposed R peak detection method |
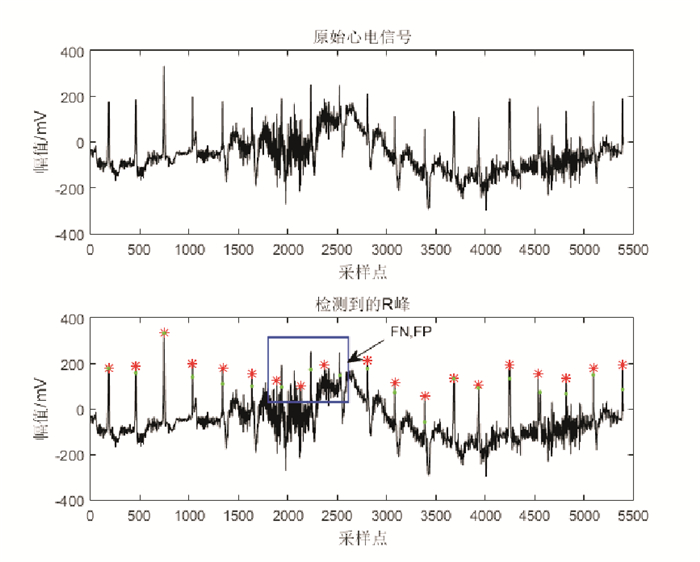
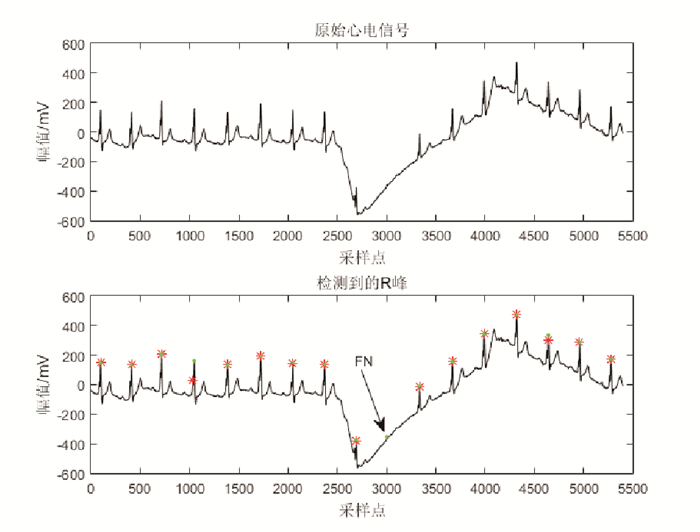
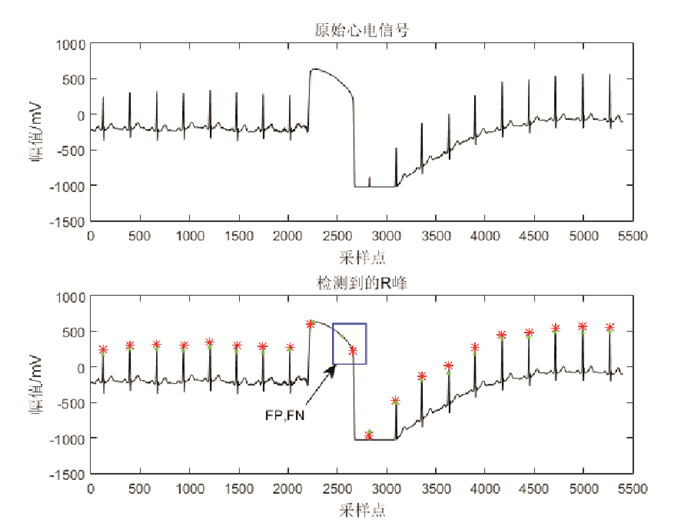
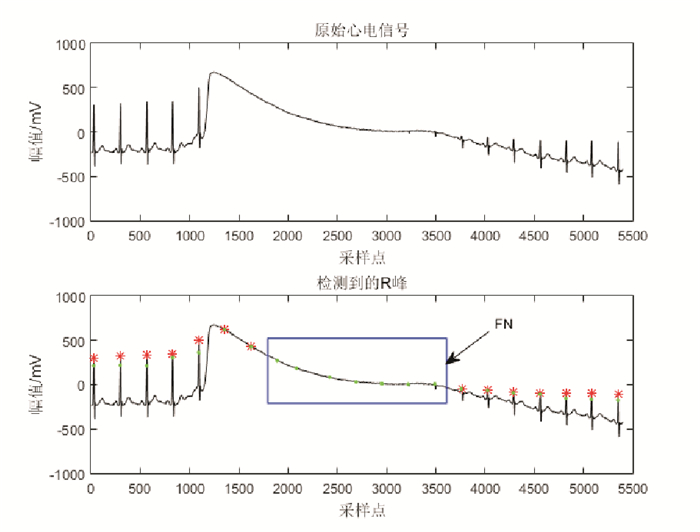
由于心电记录104,111和208中含有严重的基线漂移和波形突变现象, 且受噪声干扰和人工干预的影响较大, 部分未被去除的噪声尖波在检测过程中被误检为R峰; 心电记录232中存在长达6s的停顿间歇, 检测过程中容易将停顿间歇内的毛刺误检为R峰, 从而造成误检个数增多; 心电记录116和208中含有众多的小振幅QRS波群, 同时208中存在大范围室性早搏现象, 这些现象均会使得漏检个数增多。图 5~10分别展示了上述5条心电记录片段(时长15s)的R峰自动检测结果。图中红色星号表示检测出的R峰, 绿色点代表真实的R峰位置。
|
图 5 含有严重肌肉噪声的ECG片段的R峰自动检测结果(记录104) Fig. 5 R peak detection result for the ECG signal with serious muscle noise (Record 104) |
|
图 6 含有严重基线漂移和突变的ECG片段的R峰自动检测结果(记录111) Fig. 6 R peak detection result for the ECG signal with serious baseline wander and abrupt changes (Record 111) |
|
图 7 含有QRS波群形态突变的ECG片段的R峰自动检测结果(记录116) Fig. 7 R peak detection result for the ECG signal with sudden changes in QRS amplitudes(Record 116) |
|
图 8 包含小QRS波群的ECG片段的R峰自动检测结果(记录116) Fig. 8 R peak detection result for the ECG signal with small QRS complexes (Record 116) |
|
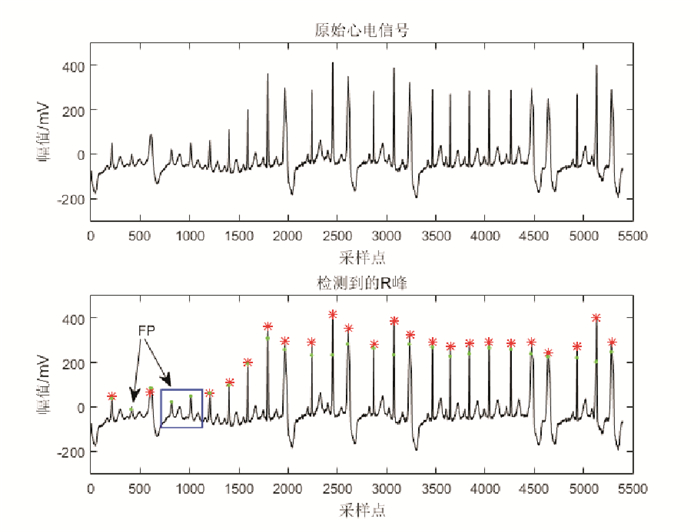
图 9 具有室性早搏和小QRS波群的ECG片段的R峰自动检测结果(记录208) Fig. 9 R peak detection result for the ECG signal with wide premature ventricular contractions (PVCs), and small QRS complexes (Record 208) |
|
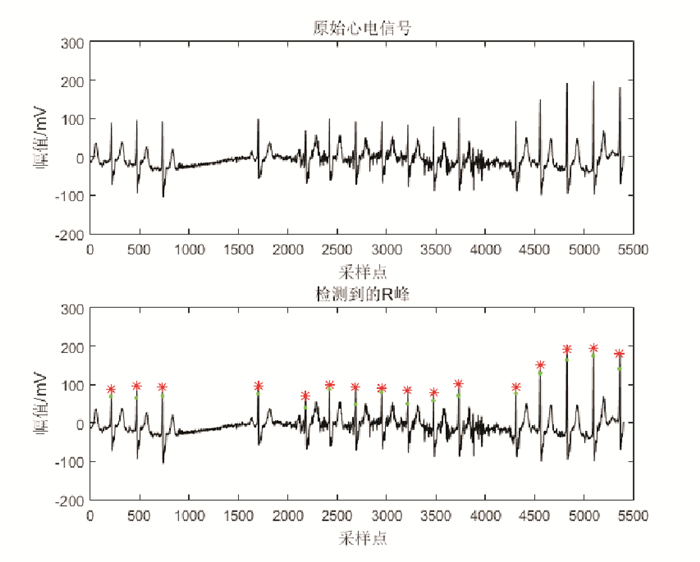
图 10 包含长达6s停顿的ECG片段的R峰自动检测结果(记录232) Fig. 10 R peak detection result for the ECG signal include long pauses up to 6s in duration (Record 232) |
本文提出了一种新的基于小波变换的R峰自动检测方法。首先, 在小波包分解和小波阈值去噪法的基础上, 本文结合基线漂移、工频干扰和肌电伪迹的频率占优特点, 提出了一种新的心电信号去噪方法, 并采用该方法对原始心电信号进行去噪处理。其次, 对去噪后的心电信号进行小波变换, 采用自适应阈值法在恰当的频率子带上检测出后候选R峰, 并经逆变换将其位置映射到原始心电信号。最后, 根据RR间期的局部变化趋势进行R峰的精细筛选, 以完成最终的R峰检测。本文选用MIT-BIH心律失常数据库中的20个心电记录对所提R峰自动检测方法进行性能评估, 采用错误检测率(DER)、真阳性率(+P)、敏感度(Se)、准确率(Acc)作为评价指标。实验结果表明, 本文所提方法具有较高的检测性能且计算速度快, 能够为临床辅助诊断提供一定的指导依据。
| [1] |
李中健, 李世锋, 申继红, 等. 心电图学系列讲座(三)——心电图一般知识[J]. 中国全科医学, 2014, 17(03): 360-362. DOI:10.3969/j.issn.1007-9572.2014.03.033 |
| [2] |
前田如矢. 一学就会心电图[M]. 中国: 华夏出版社, 2010.
|
| [3] |
YEH Y, WANG W. QRS complexes detection for ECG signal:The difference operation method[J]. Computer Methods and Programs in Biomedicine, 2008, 91(3): 245-254. DOI:10.1016/j.cmpb.2008.04.006 |
| [4] |
PAN J, TOMPKINS W J. A real-time QRS detection algorithm[J]. IEEE Transactions on Biomedical Engineering, 1985, 32(3): 230-236. |
| [5] |
HAMILTON P S, TOMPKINS W J. Quantitative investigation of QRS detection rules using the MIT/BIH arrhythmia database[J]. IEEE Transactions on Biomedical Engineering, 1986, 33(12): 1157-1165. |
| [6] |
ARZENO N M, DENG Z, POON C, et al. Analysis of first-derivative based QRS detection algorithms[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(2): 478-484. DOI:10.1109/TBME.2007.912658 |
| [7] |
BENITEZ D, GAYDECKI P, ZAIDI A, et al. The use of the Hilbert transform in ECG signal analysis[J]. Computers in Biology and Medicine, 2001, 31(5): 399-406. DOI:10.1016/S0010-4825(01)00009-9 |
| [8] |
HONGYAN X, MINSONG H. A new QRS detection algorithm based on empirical mode decomposition[C]//International Conference on Bioinformatics and Biomedical Engineering, 2008: 693-696. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4535049
|
| [9] |
SUAREZ K, SILVA J, BERTHOUMIEU Y, et al. ECG beat detection using a geometrical matching approach[J]. IEEE Transactions on Biomedical Engineering, 2007, 54(4): 641-650. DOI:10.1109/TBME.2006.889944 |
| [10] |
ABIBULLAEV B, SEO H D. A new QRS detection method using wavelets and artificial neural networks[J]. Journal of Medical Systems, 2011, 35(4): 683-691. DOI:10.1007/s10916-009-9405-3 |
| [11] |
杨福生. 小波变换的工程分析与应用[M]. 北京: 科学出版社, 1999.
|
| [12] |
GOMES P, SOARES F, CORREIA J H, et al. ECG data-acquisition and classification system by using wavelet-domain hidden markov models[C]//International Conference of the Ieee Engineering in Medicine and Biology Society, 2010: 4670-4673. https://www.researchgate.net/publication/49627438_ECG_Data-Acquisition_and_Classification_System_by_Using_Wavelet-Domain_Hidden_Markov_Models
|
| [13] |
ADDISON P S. Wavelet transforms and the ECG: a review[J]. Physiological Measurement, 2005, 26(5). |
| [14] |
DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [15] |
DONOHO D L, JOHNSTONE I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432): 1200-1224. DOI:10.1080/01621459.1995.10476626 |
| [16] |
ZHANG Q, WANG L, GAO P, et al. An innovative wavelet threshold denoising method for environmental drift of fiber optic gyro[J]. Mathematical Problems in Engineering, 2016, 1-8. |
| [17] |
GOLDBERGER A L, AMARAL L A, GLASS L, et al. PhysioBank, PhysioToolkit, and PhysioNet components of a new research resource for complex Physiologic signals[J]. Circulation, 2000, 101(23): 215-220. DOI:10.1161/01.CIR.101.23.e215 |
| [18] |
MANIKANDAN M S, SOMAN K P. A novel method for detecting R-peaks in electrocardiogram (ECG) signal[J]. Biomedical Signal Processing and Control, 2012, 7(2): 118-128. DOI:10.1016/j.bspc.2011.03.004 |
 2018, Vol. 48
2018, Vol. 48
