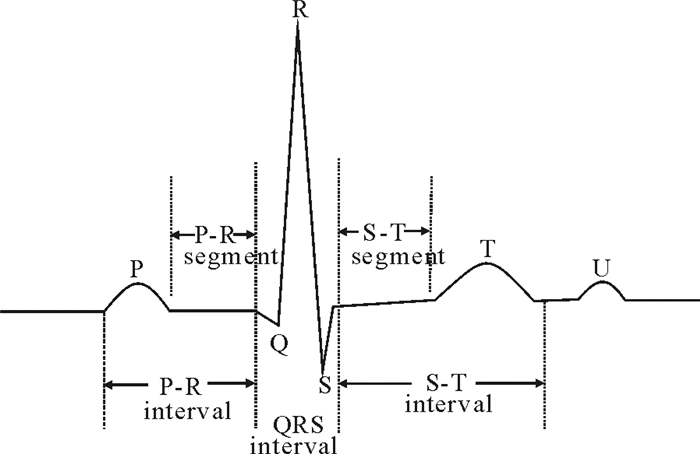
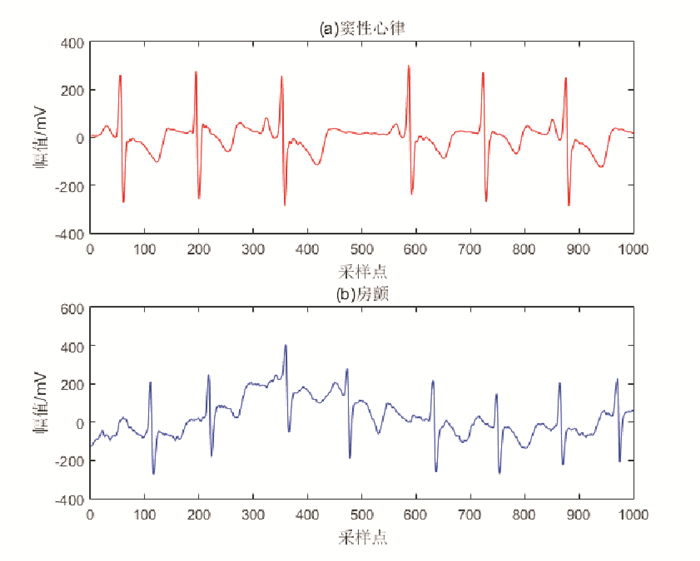
房颤, 又称心房颤动, 是临床上最常见的心律失常。房颤的发作是由于心房肌丧失了正常有规律的收缩活动, 而代之以快速不规则的房颤波, 发作时患者通常会有心悸、乏力、眩晕等症状, 严重者可诱发或加重心力衰竭, 甚至引起脑卒中[1-2]。心电图(Electrocardiogram, ECG)是由心电图仪记录反映心脏兴奋的电活动过程, 对房颤的诊断与治疗具有重要的参考价值[3]。图 1显示一个正常心动周期内的心电图波形, 其中P波表示心房去极化过程, QRS复合波表示心室去极化过程, T波表示心室复极化过程[4]。而当阵发性房颤发作时, 心房壁各部位出现杂乱无序的兴奋, 导致心脏无法正常收缩, 在心电图上通常表现为(见图 2):①P波消失, 代之以大小不等、间隔不匀、形态不同的f波(也称为房颤波, 频率在350~600次/分); ②RR间期不规则且伴有心率过速[5]。
|
图 1 一个正常心动周期的心电图波形 Fig. 1 ECG of a normal cycle |
|
图 2 窦性心律与房颤心电 Fig. 2 Sinus rhythm and atrial fibrillation |
根据房颤发作持续时长, 可分为阵发性房颤、持续性房颤和永久性房颤。由于阵发性房颤发作突然且持续时间短暂, 临床上易被漏诊, 从而往往需要长时程的心电监测。随之而产生的海量心电数据, 使得医生根据经验进行视觉诊断这一传统方法就变得十分耗时。此外, 对于阵发性房颤在心电图上所表现出的短暂且微弱的波形变化, 仅依靠视觉观察往往难以捕捉, 从而造成较多漏诊。因此, 展开关于阵发性房颤自动检测的研究具有十分重要的临床意义。
近年来, 阵发性房颤的自动检测受到了越来越多研究者的关注。洛伦兹散点图(Lorenz plot)作为信号在相空间上的几何表示, 能够揭示心电信号中心率变异的非线性特征, 因此被广泛应用于房颤心电的特征提取[6-9]。文献[10-11]中指出, 心律失常状态下的洛伦兹散点图主要呈现鱼雷形、短棒形、扇形、梭形和复杂形等, 而窦性心律主要呈现彗星状; Hargittai等人在文献[12]中提出了dRR洛伦兹散点图主要分析了早搏和房颤在该散点图上的特征, 其中房颤表现为不规则发散的图形, 早搏的图形分为几个明显的群; Lian等人在文献[13]中提出了RdR洛伦兹散点图, 并系统分析了房颤、室性早搏、二联律、三联律等心律失常在该散点图上的表现特点; Chen等人在文献[14]中采用三维洛伦兹散点图进行刻画并得出窦性心律呈现彗星状, 而心律失常则呈现漏斗、心形或不规则图形等。上述方法均是通过刻画RR间期的变化规律来提取特征, 这就需要将R峰检测作为预处理, 使得最终的房颤检测结果会直接受R峰检测性能好坏的影响[15]。基于此, 本文采用散点图对原始心电信号直接刻画, 从中提取相应的度量指标以反映正常心电与房颤心电在散点图上的表现差异, 并将其融合作为房颤心电特征。最后, 结合超限学习机(ELM)完成阵发性房颤的自动检测, 并在MIT-BIH心房颤动数据库上验证所提方法的有效性。
1 方法阵发性房颤的自动检测本质上是一个模式识别问题。本小节首先介绍ECG信号的去噪过程; 其次, 从去噪后的ECG信号中提取恰当的房颤心电特征; 最后, 采用超限学习机完成阵发性房颤的自动检测。
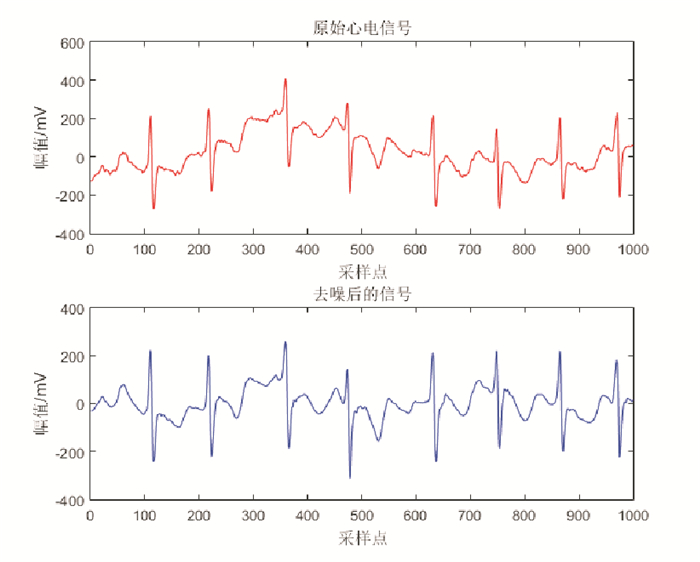
1.1 数据去噪心电信号在采集过程中易受各种背景噪声的干扰, 主要包含工频干扰、肌电干扰和基线漂移。本文分别采用50Hz陷波滤波器、35Hz低通数字滤波器及0.2Hz巴特沃兹高通滤波器, 去除工频干扰、肌电干扰及基线漂移。图 3显示了一个心电信号片段(时长4s)去噪前后的效果。
|
图 3 心电信号的去噪效果 Fig. 3 The performance of ECG denoising |
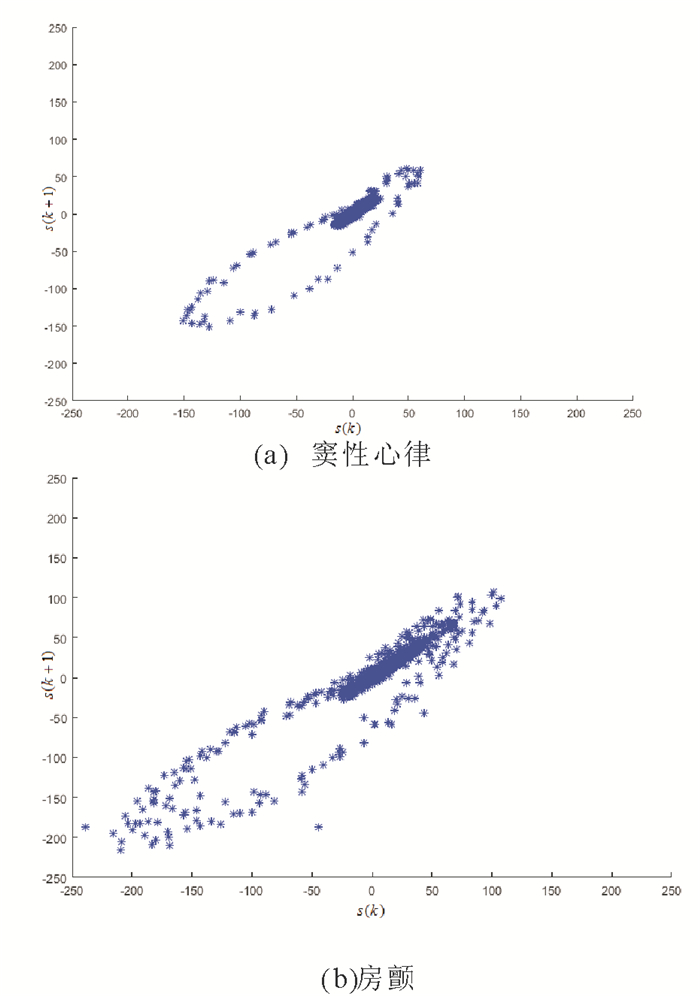
给定心电信号S={s(1), s(2), …, s(N)}。其中N表示心电信号的长度。图 4为正常心电和房颤心电所对应的散点图。从图中可以看出, 相比于正常心电的散点图, 房颤心电的散点图中分布在左下方区域、右上方区域以及偏离y=x轴的散点较多, 分布较为分散。因此本文采用3个度量指标来刻画其散度差异, 并作为信号S的房颤心电特征。本文所提特征提取方法总结如下:
|
图 4 窦性心律、房颤发作时对应的散点图 Fig. 4 The corresponding scatter diagramof sinus rhythm and atrial fibrillation |
步骤1 将信号S划分为M个等长的心电片段Si={si(1), si(2), …, si(n)}, i=1, 2, …, M。
步骤2 刻画心电片段Si在坐标轴XOY上的散点图(见图 4), 并记为
| $ {P^i} = \left\{ {P_k^i:k = 1,2, \cdots ,n - 1} \right\}。$ |
其中Pki=(si(k), si(k+1))。
步骤3 计算散点图Pi的重心
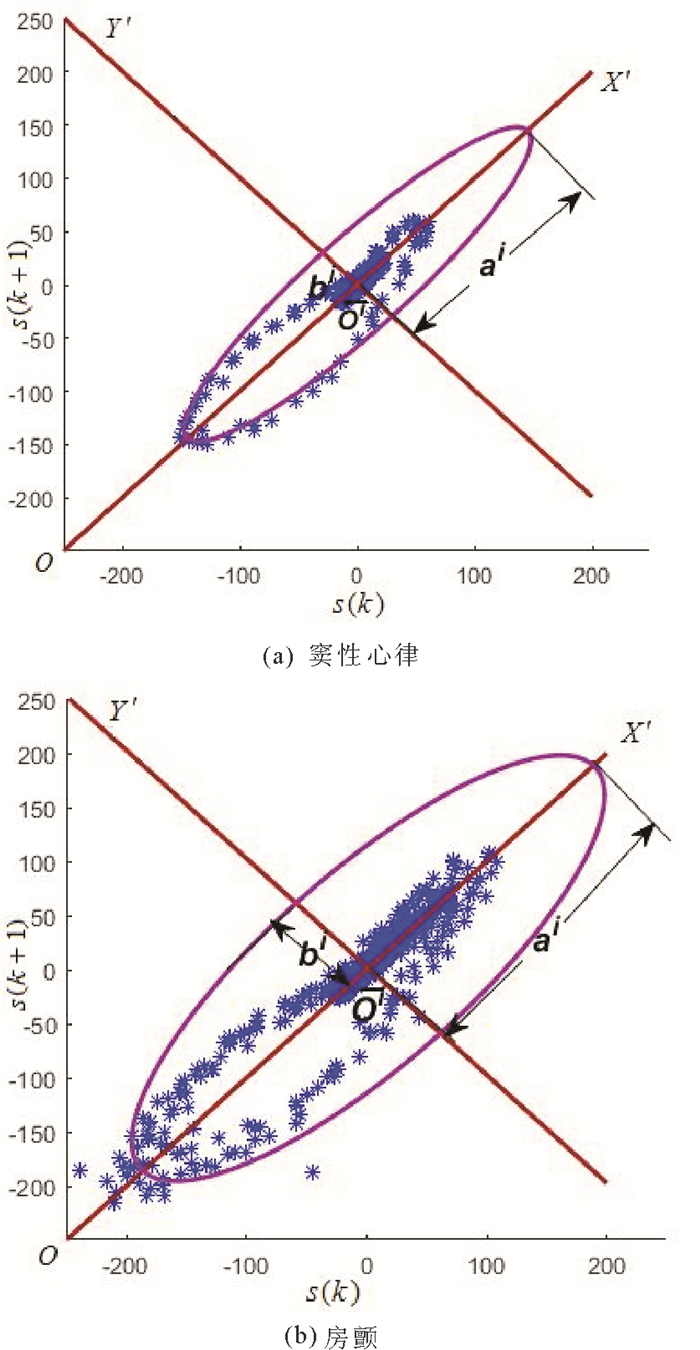
|
图 5 散点图对应的98%的置信椭圆 Fig. 5 98% confidence ellipse corresponding to the scatter graph |
步骤4 分别计算心电片段Si的置信椭圆面积FAi、置信距离散度fDDi和置信角散度fADi如下:
| $ F_A^i = {\rm{ \mathsf{ π} }}{a^i}{b^i}, $ |
| $ f_{DD}^i = \frac{{\sum\limits_{k = 1}^n {\left[ {d\left( {{s^i}\left( k \right),O} \right) - \overline {{d^i}} } \right]} }}{n}, $ |
| $ f_{AD}^i = \frac{{\sum\limits_{k = 1}^n {\left[ {\phi \left( {{s^i}\left( k \right),O} \right) - \overline \phi } \right]} }}{n}。$ |
其中ai, bi分别表示椭圆Ei的长轴与短轴; d(·)表示欧式距离,
记Fi=(FAi, fDDi, fADi)T, 并称之为心电片段Si的融合特征。于是,
| $ F = \left( {{F^{{1^{\rm{T}}}}},{F^{{2^{\rm{T}}}}}, \cdots ,{F^{{M^{\rm{T}}}}}} \right) $ |
即构成了信号S的融合特征。
1.3 超限学习机超限学习机是2006年由Huang等人提出的一种新的快速学习算法[16]。相对于传统的学习算法, ELM具有学习速度快、无需迭代调整隐变量等优点, 已被广泛应用于各种分类和回归问题。
输入样本数据集{(Xi, ti)}i=1N, 其中Xi=(Xi1, …, Xim)T
| $ {o_j} = \sum\limits_{i = 1}^S {{\beta _i}g\left( {{\mathit{\boldsymbol{W}}_i} \cdot {X_j}{b_i}} \right)} ,j = 1, \cdots ,N, $ |
其中Wi=(wi1, wi2, …, win)T为连接输入层与第i个隐单元的权重向量, βi为连接第i个隐单元和输出层的权重向量, bi是第i个隐层单元的阈值, Wi·Xj为Wi和Xj的内积。当网络的实际输出等于期望输出时, 则有
| $ \sum\limits_{i = 1}^S {{\mathit{\boldsymbol{\beta }}_i}g\left( {{\mathit{\boldsymbol{W}}_i} \cdot {X_j} + {b_i}} \right)} = {t_j},j = 1, \cdots ,N。$ |
在ELM运算过程中, 隐层输入权重Wi和阈值bi随机确定, 则隐层输出矩阵H被唯一确定。这样, 神经网络中的训练问题即转化为求解线性方程组
| $ \mathit{\boldsymbol{H\beta }} = \mathit{\boldsymbol{T}} $ |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \\ {\left( {\begin{array}{*{20}{c}} {g\left( {{W_1} \cdot {x_1} + {b_1}} \right)}& \cdots &{g\left( {{W_S} \cdot {x_1} + {b_L}} \right)}\\ \vdots &{}& \vdots \\ {g\left( {{W_1} \cdot {x_N} + {b_1}} \right)}& \cdots &{g\left( {{W_S} \cdot {x_N} + {b_1}} \right)} \end{array}} \right)_{N \times S}}, \end{array} $ |
| $ \mathit{\boldsymbol{\beta }} = {\left( {{\beta _1},{\beta _2}, \cdots ,{\beta _S}} \right)^{\rm{T}}},\mathit{\boldsymbol{T}} = {\left( {{t_1},{t_2}, \cdots ,{t_N}} \right)^{\rm{T}}}。$ |
本小节采用MIT-BIH房颤数据库中的部分心电记录来验证本文所提方法的可行性与有效性。
2.1 心电数据本文使用的心电信号均来自于MIT-BIH心房颤动数据库, 该数据库共包含25个心电记录, 采样率为250Hz分辨率为12bit[17-18]。本文从中随机选用6个时长为1h的心电记录进行数值实验, 所有实验均在Matlab R2016b中运行。
2.2 实验结果与分析本文采用50Hz陷波滤波器、35Hz低通数字滤波器及0.2Hz巴特沃兹高通滤波器对原始心电信号进行去噪, 并将去噪后的心电信号进行无重叠分段处理, 每个心电片段长度为4s(1 000个采样点)。在实验过程中, 所有数据被随机均分为训练集和测试集。为了降低随机均分所导致的训练集和测试集中不同类数据点的不均衡, 本文将这种随机均分的实验执行50次, 并取50次实验的平均结果作为最终分类性能的度量。
在构建置信椭圆时, 本文采用ROC曲线实现最佳置信参数U%的选取。图 6为参数U%从95%开始, 按1%的步长增加至99%所得的ROC曲线。从图 6可以看出, 当参数U%=98%时, ROC曲线下包围的面积AUC最大, 表明分类性能最好。
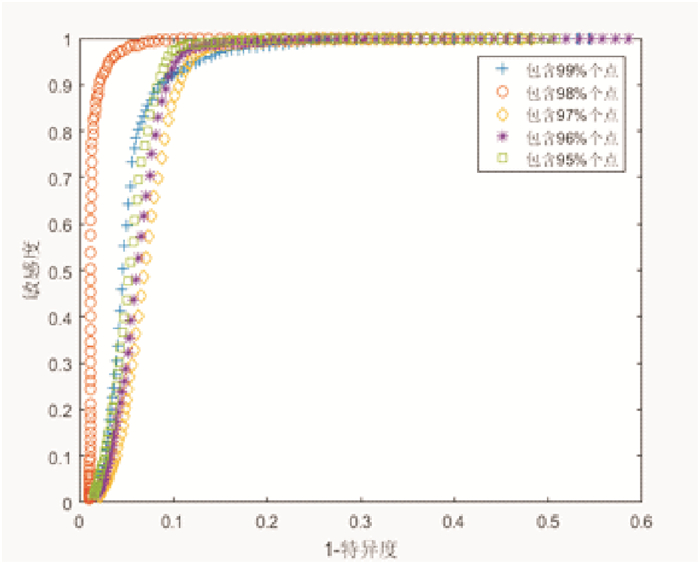
|
图 6 置信椭圆的参数选取 Fig. 6 Determination of parameter U |
在ELM中, 激活函数选取为Sigmoid函数, 隐节点选取为可加型节点, 并通过训练准确率来确定最佳隐节点个数。图 7为采用混合数据进行训练时, 隐节点个数从5开始, 以5为步长增加到50所对应的分类准确率。从图 7可以看出, 当隐节点个数为40时, 分类准确率可达到最大94.34%。
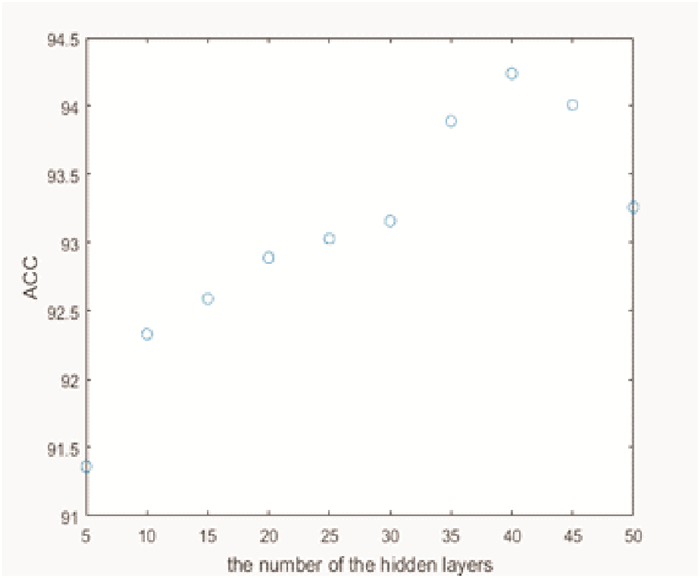
|
图 7 ELM中不同隐节点在训练集上的准确率 Fig. 7 Accuracy of different hidden nodes on training set in ELM |
本文采用准确率(accuracy)、敏感度(sensitivity)以及特异度(specificity)作为评估算法的度量指标分别定义为:
| $ {\rm{accutacy}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{FN}} + {\rm{TN}} + {\rm{FP}}}} \times 100\% , $ |
| $ {\rm{sensitivity}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}} \times 100\% , $ |
| $ {\rm{specificity}} = \frac{{{\rm{TN}}}}{{{\rm{FN}} + {\rm{FP}}}} \times 100\% 。$ |
其中TP(true positive)为真阳性, 表示实际为发作心电且被正确检测为发作心电; FP(false positive)为假阳性, 表示实际为正常心电却被错误检测为发作心电; TN(true negative)为真阴性, 表示实际为正常心电且被正确检测为正常心电。FN(false negative)为假阴性, 表示实际为发作心电且被错误检测为正常心电。
为了检验本文所提取融合特征的可行性与有效性, 首先分别对6位病人进行个人5倍交叉验证, 即将每个患者的心电信号平均分为五等份, 其中4/5用于训练, 1/5用于测试, 进行五次后取其平均结果作为最终的分类性能指标, 试验结果如表 1所示。从表 1可以看出本文提出的基于融合特征的自动检测方法对6个病人都具有较好的检测效果, 说明所提特征能够很好地区分正常心电与房颤心电。
|
|
表 1 个人5倍交叉验证 Tab. 1 Personal 5 fold cross validation |
为了验证本文所提取方法具有普适性, 进一步对6位病人的数据进行混合检验, 即将其中5个人的心电信号混合后作为训练集, 其余1个人的心电信号作为测试集, 实验结果如表 2所示。从表 2可以看出, 此融合特征对于混合数据同样有良好的检测效果, 说明此特征具有较高的普适性, 能够在临床应用中有效实现阵发性房颤的自动检测。对比表 1和表 2中的实验结果, 发现用混合数据的实验结果低于个人数据的实验结果, 这是由不同患者间的个体差异所造成。
|
|
表 2 混合数据检验 Tab. 2 Mixed data checking |
本文提出了一种新的房颤心电特征提取方法。首先采用50Hz的陷波滤波器、35Hz的低通数字滤波器、0.2Hz巴特沃兹高通滤波器进行数据去噪, 分别去除工频干扰、肌电干扰和基线漂移; 其次, 将去噪后的心电信号分割成若干等长片段, 绘制每个心电片段的散点图, 并计算散点图的置信椭圆面积、置信距离散度和置信角散度进行融合作为心电特征; 最终采用MIT-BIH房颤数据库中的心电信号, 结合超限学习机(ELM)完成阵发性房颤的自动检测。数值实验结果表明, 本文所提出的阵发性房颤自动检测方法具有较高的检测性能, 为临床诊断提供一定的辅助作用。
| [1] |
陆悠, 唐蓉蓉, 毛家亮, 等. 阵发性房颤、房扑的心电散点图特征[J]. 临床心电学杂志, 2014, 23(4): 271-273. |
| [2] |
向晋涛. 心电散点图表达的心脏电生理现象[J]. 临床心电学杂志, 2012, 21(1): 6-10. |
| [3] |
LI C, ZHENG C, TAI C. Detection of ECG characteristic points using wavelet transforms[J]. IEEE transactions on bio-medical engineering, 1995, 42(1): 21. DOI:10.1109/10.362922 |
| [4] |
李方洁, 沈红军, 郭小玉, 等. 心房颤动伴短联律间期宽QRS波散点图的类型及特征[J]. 中国心脏起搏与心电生理杂志, 2011, 25(1): 41-44. |
| [5] |
BRENNAN M, PALANISWAMI M, KAMEN P. Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability?[J]. IEEE Transactions on Biomedical Engineering, 2001, 48(11): 1342-1347. DOI:10.1109/10.959330 |
| [6] |
STRUMILLO P, RUTA J. Poincare mapping fordetecting abnormal dynamics of cardiac repolarization[J]. Engineering in Medicine andBiology Magazine, 2002, 21(1): 62-65. DOI:10.1109/51.993195 |
| [7] |
TSUBOI K, DEGUCHI A, HAGIWARA H. Relationship between heart rate variability using Lorenz plot and sleep level[C]//Engineering in Medicine and Biology Society. IEEE, 2010: 5294. http://europepmc.org/abstract/MED/21096062
|
| [8] |
PARK J, LEE S, JEON M. Atrial fibrillation detection by heart rate variability in Poincareplot[J]. Bio Medical Engineering Online, 2009, 8(1): 38. DOI:10.1186/1475-925X-8-38 |
| [9] |
CONTRERAS P, CANETTI R. MIGLIARO ECorrelations between frequency-domain HRV indices and lagged Poincare plot width in healthy and diabetic subjects[J]. Physiologicalmeasurement, 2007, 28(1): 85-94. |
| [10] |
WANG W, WEI Y, GUAN N, et al. The automaticdetectionand analysis of Electrocardiogram based on Lorenz plot[J]. IEEE Proceedings of Robotics and Biomimetics, 2016, 644-649. |
| [11] |
王恒迪, 朱坚民, 蔺利峰, 等. 洛伦兹散点图及其在房颤自动诊断中的应用[J]. 生物医学工程学杂志, 2007, 24(2): 449-452. |
| [12] |
HARGITTAI S. Is it possible todetect atrial fibrillation by imply using RR intervals?[J]. IEEE Proceedings of Computing in Cardiology, 2014, 897-900. |
| [13] |
LIAN J, WANG L, MUESSIG D. A simplemethod todetect atrial fibrillation using RRintervals[J]. American Journal of Cardiology, 2011, 107(10): 1494-1497. DOI:10.1016/j.amjcard.2011.01.028 |
| [14] |
CHEN L, ZHANG K, LIU K Q. Study on 3D Lorenz plots of heart rate variability[J]. Nanoscience andNanotechnology Letters, 2013, 5(2): 248-252. DOI:10.1166/nnl.2013.1516 |
| [15] |
RUAN X, LIU C, LIU C, et al. Automatic detection ofatrial fibrillation using RR interval signal [C]//International Conference on Biomedical Engineering and Informatics. IEEE, 2011, 28 (1): 644-647. http://www.researchgate.net/publication/220715249_Automatic_detection_of_atrial_fibrillation_using_R-R_interval_signal
|
| [16] |
HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70: 489-501. DOI:10.1016/j.neucom.2005.12.126 |
| [17] |
MOODY G B, MARK R G. The impact of the MIT-BIH arrhythmia database[J]. IEEE Engineering in Medicine and Biology Magazine, 2001, 20(3): 45-50. DOI:10.1109/51.932724 |
| [18] |
CASALEGGIO A. Differences on the correlation dimension of MIT-BIH ECG database recordings[J]. Computers in Cardiology Conference, 1993, 539-542. |
 2018, Vol. 48
2018, Vol. 48