1 Introduction

Dependence or association modeling between two random variables plays an important role in statistics literature.Measuring the strength of various association has an extensive body of literature.The most prominent and popular measures of associations between random variables include but not limited to Pearsons correlation coefficient^[1], Spearmans ρ^[2] and Kendalls τ^[3].

However, these measures are not suitable if the data shows the non-linear relationship between the variables.This is because Pearsons correlation coefficient r only measures the linear relationship of random variables, Spearmans ρ and Kendalls τ are measures of monotonic relationships. As a motivation, we provide a simple example below.

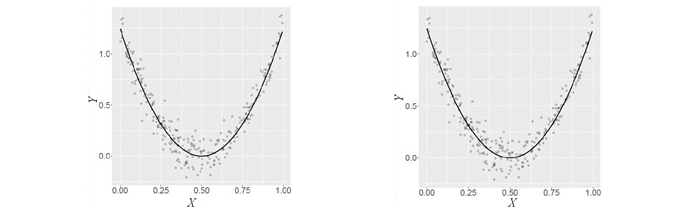
Example 1  Assume X_i, Y_i, i=1, …, n, are identical and independent distributed(i.i.d.) random variables with Y_i=5(X_i-0.5)²+σ∈_i, X_i follows uniform distribution on [0, 1], and ∈_i, i=1, …, n are i.i.d. standard normal random variables. Thus, the true model considered here is that the random variable Y is a non-linear(quadratic) function of X(not vice versa). We simulate the data for n=300, 1 000 and provide the scatter plots in Fig. 1.

The plots in Fig. 1 indicate strong nonlinear relationship between the variables, however, the Pearson′s correlation coefficient r=0.021, Spearmans ρ=-0.008, and Kendalls τ=-0.004 for n=300 and r=-0.02, ρ=-0.003, and τ=-0.009 for n=1 000 are all very small (close to zero).

Example 1 shows that it is in contrast to the common belief that linear relationship is more revealing about the underlying random variables than nonlinear relationship. We expect that these problems would be even more severe and more difficult to detect for high dimensional predictors.

In statistical association analysis, it is often assumed the relevant random variable follows some parametric distribution families. The parametric approach often suffers from possible shortcomings induced by the misspecification of the parametric family. Additionally, even for the same type of association and same marginal distribution the associated joint distributions could be very different.

Therefore, a natural questions is how we can determine or quantify the general association(linear or nonlinear) between random variables X and Y by utilizing a non-parametric approach. In this article, we review a new asymmetric dependence measure based on subcopula based regression which was proposed by Wei and Kim^[4] and focus on the association analysis between continuous random variables considering toth interaction directionality and nonlinearity. The rest of the article is structured as follows. Section 2 briefly reviews the definition of the subcopula and the asymmetric dependence measure for contingency based on subcopula based regression proposed in^[4] (Wei and Kim, 2017). Then, section 3 examines the use of the measure for nonlinear association for data generated from continuous random variables. We end this article by a conclusion section.

2 Review on subcopula and Subcopula-based measure of asymmetric association for contingency tables

In this section, we briefly reviews the definition of subcopulas and the asymmetric dependence measure for contingency based on subcopula based regression which was proposed in^[4] (Wei and Kim, 2017).

2.1 Review on subcopula

Copula is a technique to introduce and investigate the dependence between variables of interests.Copulas are frequently applied in many application areas including fiance^[5-8], insurance^[9] (Jaworski et al., 2010), risk management^[10] (Embrechts et al., 2002), health^[11] (Eluru et al., 2010) and environmental sciences^[12](Zhang and Singh, 2007).Here, we briefly review the definition of the bivariate subcopula and copula function.For more details about the copula and dependence concepts in terms of subcopulas and copulas, see^[13-17] (Joe, 2014;Nelsen, 2006;Wei et al., 2015;Wei and Kim, 2017).

Definition 1^[14]  (Nelsen, 2006) A bivariate subcopula (or 2-subcopula) is a function C^S: D₁×D₂$\mapsto $[0, 1], where D₁ and D₂ are subsets of [0, 1] containing 0 and 1, satisfying following properties:

(a) C^S is grounded, i.e., C^S(u, 0)=C^S(0, ν)=0;

(b) For every u, ν∈[0, 1], C^S(1, ν)=ν and C^S(u, 1)=u;

(c) C^S is 2-increasing in the sense that, for any u₁≤u₂, ν₁≤ν₂ with u_i, ν_i∈[0, 1], i=1, 2,

vol C^S(J)=C^S(u₂, ν₂)-C^S(u₂, ν₁)-C^S(u₁, ν₂)+C^S(u₁, ν₁)≥0,

A bivariate copula (or 2-copula) C(u, ν) is a subcopula with D₁=D₂=[0, 1].

From the Definition 1 a subcopula(copula) is a (unconditional) cumulative distribution function (CDF) on D₁×D₂([0, 1]).The condition (b) indicates a 2-copula C is a bivariate CDF with uniform margins. Let X and Y be two random variables (discrete or continuous) with the joint CDF H(x, y) and marginal CDF F(x) and G(x).There exists a subcopula function C^S such that H(x, y)=C^S(F(x), G(y)) by the Sklars theorem^[18] (Sklar, 1959).Furthermore, if X and Y are both continuous random variables, then there exist a unique copula C such that H(x, y)=C(F(x), G(y)).

2.2 Subcopula-based measure of asymmetric association for contingency tables

Wei and Kim (2017)^[4] proposed a new asymmetric association measure for the contingency table by utilizing subcopula based regression. Suppose we have a two-way contingency table that cross-classifies n subjects/units according to I categories of the row variable and J categories of the column variable and let the matrix of the joint cell proportions in the I×J contingency table be P={p_ij} where i=1, …, I, j=1, …, J and $\sum\limits_{i=1}^{I}{\sum\limits_{j=1}^{J}{{{p}_{ij}}=1}}$. Furthermore, p_i·=$\sum\limits_{j=1}^{J}{{{p}_{ij}}}$ and ${{p}_{\cdot j}}-\sum\limits_{j=1}^{J}{{{p}_{ij}}}$ denote the i-th row marginal relative frequency and j-th column marginal relative frequency, respectively.Then, the supports for the subcopula C^S associated with the table can be derived below,

$ {{u}_{i}}=\sum\limits_{s=1}^{i}{{{p}_{s}}.\ \ \text{and}\ \ {{v}_{j}}}=\sum\limits_{t=1}^{j}{p\cdot t.} $

(1)

The marginal p.m.f.s and the joint p.m.f of C^s associated with the table are, respectively, p₀(u_i)=p_i·, p₁(ν_j)=p_·j, c^s(u_i, v_i)=p_ij. Furthermore, the conditional p.m.f.s and the conditional p.m.f.are, respectively,

$ \begin{align} & {{p}_{j|i}}={{c}_{V|U}}\left( {{v}_{j}}|{{u}_{i}} \right)=\frac{c\left( {{u}_{i}}, {{v}_{j}} \right)}{{{p}_{0}}\left( {{u}_{i}} \right)}=\frac{{{p}_{ij}}}{{{p}_{i\cdot }}} \\ & {{p}_{i|j}}={{c}_{U|V}}\left( {{u}_{i}}|{{v}_{j}} \right)=\frac{c\left( {{u}_{i}}, {{v}_{j}} \right)}{{{p}_{1}}\left( {{v}_{j}} \right)}=\frac{{{p}_{ij}}}{{{p}_{\cdot j}}}. \\ \end{align} $

(2)

Then, one can quantitatively measure the asymmetric dependence between the two variablex X and Y in an I×J contingency table.

Definition 2  (Wei and Kim, 2017)^[4] Given an I×J contingency table, a measure of subcopula-based asymmetric association of column variable Y on row variable X and of row variable X on column variable Y are defined as follows, respectively:

$ \rho _{\left( X\to Y \right)}^{2}=\frac{{{\sum\limits_{i=1}^{I}{\left( \sum\limits_{j=1}^{J}{{{v}_{j}}{{p}_{j|i}}-\sum\limits_{j=1}^{J}{{{v}_{j}}{{p}_{\cdot j}}}} \right)}}^{2}}{{p}_{i\cdot }}}{{{\sum\limits_{j=1}^{J}{\left( {{v}_{j}}-\sum\limits_{j=1}^{J}{{{v}_{j}}{{p}_{\cdot j}}} \right)}}^{2}}{{p}_{\cdot j}}}, $

and

$ \rho _{\left( Y\to X \right)}^{2}=\frac{\sum\limits_{j=1}^{J}{{{\left( \sum\limits_{i=1}^{I}{{{u}_{i}}{{p}_{i|j}}-\sum\limits_{i=1}^{I}{{{u}_{i}}{{p}_{i\cdot }}}} \right)}^{2}}{{p}_{\cdot j}}}}{{{\sum\limits_{i=1}^{I}{\left( {{u}_{j}}-\sum\limits_{i=1}^{I}{{{u}_{i}}{{p}_{i\cdot }}} \right)}}^{2}}{{p}_{i\cdot }}}. $

(3)

The subcopula-based asymmetric association measure in Definition 2.2 has several nice properties.For example, one can identify the nonlinear or asymmetric relation between the variables in a two-way contingency table.To be specific, if a random variable Y is a function of random variable X almost surely, then ρ_(X→Y)²=1, and if X and Y are independent, then ρ_(X→Y)²=ρ_(Y→X)²=0 (for more details, see Proposition 3.2 in^[4] (Wei and Kim, 2017)).Motivated by this property, we applied the subcopula-based asymmetric association measure in Definition 2 on the continuous random variables in next section.

3 One example for continuous random variables

The asymmetric association measure ρ² in Definition 2 measures the association for the discrete random variable associated with the two-way contingency table without parametric assumptions on the joint distributions.In this section, we develop one procedure to apply the subcopula-based asymmetric association measure on continuous random variables and illustrate the procedure along with the Example 1 as follows.

First, in order to apply asymmetric association measure ρ² in Definition 2 on the continuous random variables, data must be quantized into categorical data.We can construct the I×I contingency table by classifying the n data points into I categories for each variable. For example, if we set I=5 for data (n=300 and n=1 000) simulated from Example 1.1, we have the following two contingency tables, Table 3.1a and 3.1a.Note that for this example, we can classify each variable with I equal-width categories, i.e., [a, a+(b-a)/I, [a+(b-a)/I, a+2(b-a)/I), …, [a+(I-1)(b-a)/I, b], where b=max{x₁, …, x_n} for X(b=max{y₁, …, y_n} for Y), a=min{x₁, …, x_n} for X(a=min{y₁, …, y_n} for Y).

Second, based on the contingency tables associated with each number of categories I obtained from the first step.The subcopula-based asymmetric association measures ρ_(X→Y)² and ρ_(Y→X)² in Eq.(3) can be estimated by using the estimators $\hat{\rho }_{\left( X\to Y \right)}^{2}$ and $\hat{\rho }_{\left( Y\to X \right)}^{2}$ in Eq.(14)^[4] in (Wei and Kim, 2017).

For example, for the two contingency tables given in Table 3.1a and 3.1a, we obtain $\hat{\rho }_{\left( X\to Y \right)}^{2}$=0.009 and $\hat{\rho }_{\left( Y\to X \right)}^{2}$=0.608 for the data set with n=300, and $\hat{\rho }_{\left( X\to Y \right)}^{2}$=0.01 and $\hat{\rho }_{\left( Y\to X \right)}^{2}$=0.647, respectively.

Third, we estimate$\hat{\rho }_{\left( X\to Y \right)}^{2}$ and $\hat{\rho }_{\left( Y\to X \right)}^{2}$ for each contingency table with category I=2, 3, …, until the asymmetric association measure converges to a "true" value.For the simulation data presented in Example 1, $\hat{\rho }_{\left( X\to Y \right)}^{2}$ are very small and close to zero for both n=300 and n=1 000, we focus on the asymmetric association measure for $\hat{\rho }_{\left( Y\to X \right)}^{2}$ below.

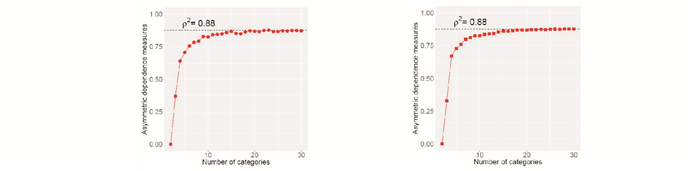
Figure 2 shows the values of the subcopula based asymmetric association measure$\hat{\rho }_{\left( X\to Y \right)}^{2}$ with respect to the number of the categories for sample size n=300 (left) and n=1 000 (right). We observe that the subcopula based asymmetry measure ρ_(X→Y)² with respect to the number of the categories for sample size n=300 (left) and n=1 000 (right).We observe that the subcopula based asymmetry measure ρ_(X→Y)² approach to a fixed value $\hat{\rho }_{\left( X\to Y \right)}^{2}$≈0.88 as the number of categories increases for both sample size n=300 and n=1 000.Therefore, $\hat{\rho }_{\left( X\to Y \right)}^{2}$ successfully detect the nonlinear association between X and Y.

4 Conclusion

In this paper, we have reviewed a subcopula-based measure of the asymmetric association for a two-way contingency table, which was proposed in (Wei and Kim, 2017)^[4]. We applied the proposed measure to a data set with the non-linear relationship and showed it can be used as a tool to detect the non-linear association. The proposed procedure is illustrated via a simulation example.