1712年, 清康熙帝爱新觉罗·玄烨(1654—1722)拒绝法国传教士傅圣泽(Jean Francoise Foucquet, 1663—1740)传入西方符号代数这一科学传播事件说明了西方传教士第一次尝试传入西方符号代数已经失败。1859年, 中国数学家李善兰(1811—1882)和英国汉学家伟烈亚力(Alexander Wylie, 1815—1887)合作翻译的我国第一本西方符号代数学著作《代数学》在上海墨海书馆顺利刊行标志着西方符号代数学开始传入我国。《代数学》的翻译出版拉开了西方符号代数学在我国传播的序幕, 并且和我国传统代数学思想有着相互的影响。《代数学》翻译的底本为英国数学家、数学史家德摩根(Augustus De Morgan, 1806—1871)在1837年所著的Element of Algebra[1]。从《代数学》翻译出版的过程和内容可以看出《代数学》受到了中国传统代数学思想的影响。特别是从整个内容体系来看, 《代数学》对晚清代数学理论的科学性和系统性有着很深的影响[2-3]。中国传统代数学是在实际生活和生产中的一些应用问题里出现的一种代数运算, 其本质上强调的是一种实际应用的运算问题, 其目的就是解决生活和生产中遇见的一些代数或几何问题的运算。但是其中也有一些纯粹数学, 即数学史家曲安京教授提出的为数学而数学[4]。中国传统代数学与西方公理化和符号化演绎体系有着不同的特点, 中国传统代数学有着自己的独特之处和发展体系的客观历史原因[5]。从译著的内容和形式上来看, 这是一种半符号化的代数学, 说明这一时期的中国传统代数学并不乐意于接受西方符号代数学体系, 同时, 也是在半接受着西方新进的符号代数学理论, 最终被西方符号数学所取代[6-7]。对这一时期的代数学西化历史研究是有着一定的必要性, 只有这样才能真正理解中国传统代数学和西方符号代数学的区别和联系, 以及他们相互影响的历史过程。当代数学大师丘成桐先生认为清末西方数学传入我国的历史过程中, 最为重要的就是李善兰和伟烈亚力合译的《代数学》和《代微积拾级》, 传入的近代符号代数学中最重要的就是译著《代数学》, 其特别指出了《代数学》是引进了西方代数学的半符号表示系统[8]。
《代数学》对于清末中国数学理论的研究和教育都有着崭新的内容体系, 李善兰创立的代数学术语和代数学符号许多沿用至今。李善兰指出不能完全排斥以前数学中所用的旧名, 也不能完全使用所创造的新名, 可以对以前的数学词汇和专业术语进行改造或者引申, 尽可能让以前的术语所包含的意思得以扩充。通过研究厘清《代数学》与中国传统代数学思想之间的相互关系和影响。要弄清楚这之间关系和影响得首先要弄清楚什么是中国传统代数学, 以及中国传统代数学的发展历史情况和对近代符号代数的影响。
1 中国传统代数学中国古代传统数学, 特别是中国传统代数学理论有着辉煌的成就。中国古代从严格意义上来说没有系统化的符号代数学理论, 但是从传统代数学本身的特征结构来说其传统代数学理论是非常发达的。中国传统代数学早期称为算术, 即以计算为主。算术是数学中最古老和最基础部分, 它主要是研究数特别是整数的性质及其运算。把数和数的性质、数和数之间的四则运算在应用过程中累积出来的规律加以总结和概括就形成了最古老算术[9]。中国传统代数学理论和代数学结构主要集中体现在几个方面:生活生产中的代数理论; 天文历法中的代数系统; 乐律中的代数学表示; 自然哲学的代数结构等。
中国传统代数学理论来源之一就是生活与生产过程中涉及的一些数值计算和算法分析。中国传统代数学中强调的是数字和数字之间的运算, 中国关于数字记录可以追溯到很早的历史。殷墟出土的甲骨文中就有一些记录数字的文献[9]。《史记》中从历史的角度记载了大禹治水过程中使用的规、矩、准、绳等几何作图和测量的工具的历史。《考工记》中包含了一些测量方面的内容, 并涉及到一般几何学知识的介绍[10]。《墨经》中有关于一些几何的定义和命题, 并且给出有穷和无穷的定义, 这是极限思想的雏形。《庄子》中的极限论述是较早出现的极限思想。《周髀算经》在数学方面提出勾股定理及普遍形式, 并且对其进行了数学证明。“日高法”是后来重差术即勾股测量法的先导, 有较复杂的开方问题和分数四则运算等[11]。其成就主要集中在代数学理论范畴, 涉及到代数方程求解和开方等问题。赵爽在其著作《周髀算经注》中创立了“勾股圆方图说”, 详细论述了勾、股、弦的各种关系, 并附如图 1进行了证明[10]。
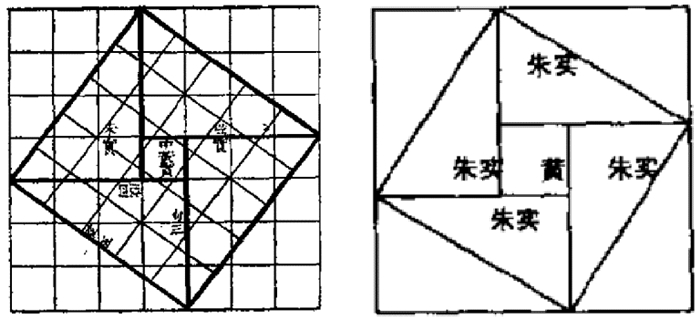
|
图 1 弦图 Fig. 1 Chordal Graph |
其中论述到“其倍弦为广袤合, 令句、股见者自乘为其实。令合自乘, 四实以减之, 开其余所得为差。以差减合, 半其余为广[11]。”这里假设x1, x2分别表示的是一个矩形的两边, 广和袤, 则x1+x2=2×弦, 又有x1·x2=棺乘, 根据题意可得广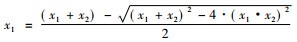
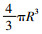
① 这结果在欧洲直到17世纪才由意大利数学家卡瓦列利(Bonaventura Cavalieri, 1598—1647)提出同一计算原理。
天文历法中的代数系统主要是在天文计算中出现的代数理论。中国古代的历法非常复杂, 因为其既观测太阳, 同时又要观测月亮。通过采用干支纪年的代数系统结构, 这就使得中国农历很难推算, 大多情况都只能靠不中断的历史记载。中国传统数学与历法中出现了大量的连分数形式并非偶然, 这一分数理论实际上就是为了满足天文历法的需要[14]。特别是刘徽(225—295)和祖冲之(429—500)关于圆周率的计算, 祖冲之推断圆周率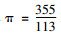
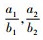
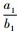
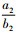
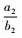
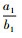
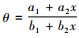
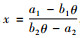
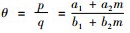
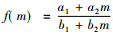
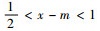
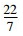
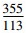
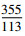
乐律中的代数学理论主要是乐器发声的构造和发声之间的一种代数关系。音乐的形成最早来自于生活和生产, 直到发展成为某种固定的旋律, 这才上升到了理论研究的高度[15]。琴弦的长度变化和粗细程度和松紧度不一样的时候, 乐器所发出的音高和音频都是不一样的。所以, 这就需要有一个严格的代数学理论来控制构造和发声直接的数学关系[16]。律学是从发声体的振动规律出发, 利用数学方法确定乐音的音高规律、音程关系等的科学。律学是由物理学中的声学理论、数学中代数计算理论和乐音理论互相渗透的一门新的学科[15]。特别是数学计算至关重要, 传统律学理论中特别注重代数学理论, 特别是代数学理论中代数运算法则和代数关系, 传统律学中“数因律起, 律以数成”是数学与律学相互渗透的体现[15]。“律吕”指的就是十二律, 其名称则是按音的高低排列顺序依次为“黄钟、大吕、太簇、夹钟、姑洗、仲吕、蕤宾、林钟、夷则、南吕、无射、应钟。”在现代乐音理论中对应的音名分别为 “C,#C,D,#D,E,F,#F,G,#G,A,#A,B。”十二个音存在严格的代数运算关系:
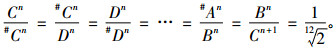
|
从这个代数关系式可以看出乐音都可以通过其中一音的升高或者降低而获得[17]。根据乐理可以得到一个公设, 也就是一个公理化表述。如五声音阶的代数推算就是利用中国传统代数学方法进行计算的, 这一文献最早记载于《管子·地员篇》中, 其中论阐述到“凡起于五音凡首, 先主一而三, 四开以九九。以是生黄钟小素之首, 以成宫。三分而益一, 为百有八, 为徵。不无有三分而去其乘, 适足, 以是生商。有三分, 而复于其所, 是以成羽。有三分而去其乘, 适足, 是以生角。”据此论述用现代数学公式表示五音算法为图 2所示演算过程。律学代数计算体系的相关比较研究采用各科综合方法进而来解决一类与代数学相关的音乐系统问题。涉及到了集合、群和域等概念。即有集合T={C(n)|n∈Z}, 若T′为乐音集, 则有T′⊂T, t(n)=#t(n-1), 可以得到:①S={t(n)|1≤n≤m}, S∪{0}对t(i)+t(j)=t((i+j)modr), r=|S∪{0}|运算是Abel群。②S∪{0}=p, S∪{0}对结论①中的加法(+p)和t(i)*pt(j)=t((i*j)modp)是域 。
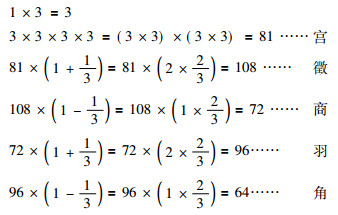
|
图 2 五音计算式 Fig. 2 Calculation formula of five sounds |
从这一代数运算图可以看出81是3的4次幂。观察整个代数运算的法则和过程, 不难看出四次除法都除以3, 显然, 81是能被3整除四次的最小整数。对于这些代数运算及其关系来说, 律学中的数本身并没有实际意义, 关键是这之间的比例关系和运算关系[18]。
自然哲学的代数结构体现在《周易》中, 其太极、阴阳、四象、八卦等理论都涉及到了几何、代数、数论等数学问题。《周易》是中国古代经典中结构最简单但内容却是最抽象之作[19-24]。从数学构成上来说, 太极八卦图是宇宙数学模式代数图, 其中, 太极化生八卦的过程从无到有, 这一无限的数学思想, 明显表达的是数0→1→2→3→4→…乃至无穷。“河出图, 洛出书, 圣人则之。河图者也, 其位一六居下, 二七居上, 三八居左, 四九居右, 五十居中。[21]”《周易》之数乃言传天地大衍之数, 是变数, 且是无穷变数, 有“象”是几何, 有“数”是数学, 是朦胧的数学科学[22]。然而, 认识事物只有从事物本身的内容以及相互联系的事物出发才能够找到正确的答案。河图洛书的本质是数学, 是中国传统文化中创造出的一项数学成果[23]。从其代数关系发现有等和关系, 也就是表现为各个纵向、横向和对角线上的三数之和为15。同时, 还存在等差关系, 洛书隐含着等差数列逻辑关系。《周易》中的这种代数结构被一些中外数学家所发现, 如莱布尼兹(Gottfried Wilhelm Leibniz, 1646—1716)接触易学理论后, 发现二进制与易学理论一定的联系[24]。显然, 《周易》科学与易经数学实践是张扬理性的巨大动力。而太极八卦图是宇宙数学模式图, 既是哲学图又是几何图数论图。河图洛书既是“木、火、土、金、水”五行之间的生克哲学图, 同时也是数论图。《周易》中的σ-代数, 概率论的公理化定义建立在测度论的基础之上, 而σ-代数是测度论中的基础内容。《易经》中的64卦相当于一个古典概率模型, 64卦的全体对应一个样本空间Ω, 共有64个样本点, 即Ω={64卦的全体}。记G={Ω所有子集构成的全体}。则G满足σ-代数的条件, 所以G是一个σ-代数。由64卦的形成过程来看, Ω中的每个样本点所出现的概率均相等, 皆为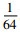
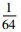
译著《代数学》中的主要内容为符号代数学理论, 当然, 有一小部分是属于分析学方面的内容[25-26]。《代数学》开篇就对代数学的中西发展史进行了论述, 特别是西方代数学史。其中论述了古希腊数学家丢番图(Diophantus, 246—330)用文字缩写形式表示未知数或者未知量, 公元250年前后, 丢番图撰写的著作《算术》(Arithmetica)中引入了表示未知数的概念, 还创立了未知数的符号表示, 其中最重要的是建立方程序这一重要的代数学思想。同时,对我国传统数学中的代数学发展历史进行了论述, 特别是伟烈亚力认为宋元时期的代数则发展到了世界领先水平。然而, 对于符号代数学来说, 真正代数程序化的是公元9世纪阿拉伯代数学家阿尔·花拉子米(al-Khowārizmī, 780—850)所著《还原与对消原理》(ilm al-jabr wal muqabalah)。其中的al-jabr意为“还原”, 即相当于是把负项移到方程另一端去而“还原”为正项。而其中的“muqabalah”意思是“对消”或“化简”, 指方程两端可以消去相同的项或者是合并同类代数项。“al-jabr”译为拉丁文“aljebra”, 英文翻译为“algebra”。1859年, 李善兰首次把“algebra”译为“代数”和“代数学”。1873年, 清末数学家华蘅芳(1833—1902)和英国传教士傅兰雅(John Fryer, 1839—1928)合译英国数学家华里司(William Wallace, 1768—1843)的《代数术》(Algebra)时, 在卷首有“代数之法, 无论何数, 皆可以任何记号代之。[27]”亦作代数, 即运用文字符号来代替数字的一种数学方法。由此可见, 其翻译之事借鉴了李善兰和伟烈亚力的翻译思想。《代数学》中只有少量运用西方代数学理论中的数学表示符号, 符号系统则是沿用中国传统代数学中的传统符号体系和李善兰和伟烈亚力二人共同创造的代数学体系[21]。李善兰和伟烈亚力在《代数学》中很独特地避免“+”,“-”与汉语数字“十”和汉语数字“一”相互之间的混淆, 取篆文的“上”、“下”二字, 即用“┸”,“┳”来表示加减符号, “┳”还表示“负”。到了后来清末的教育学堂正是开办和清末数学的全面提升起来后, “+”、“-”符号才得以广泛使用, 并且沿用至今。然而, 其中的“×”,“÷”则是李善兰直接引用于原著, 然而, 传统代数学中的乘除法有着不一样特别的称谓, 我国古代没有创立乘除法符号。关于直接使用等号“=”的使用也是从李善兰开始的, 开始使用的是一个长等号“==”, 慢慢演变成为“=”。对于符号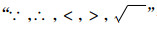
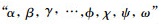
从内容来看, 《代数学》的主要内容有方程理论、代数之表达式、极限、二项式定理、超越函数和级数等内容。这些大部分是代数学的基础内容, 但是, 其中也有分析学的内容体系。《代数学》中这些内容是近代数学发展的一个过渡, 是发展成为更为高等的数学内容的基础。代数方程理论, 《代数学》中的方程理论主要是介绍一元代数方程, 而在解方程中没有谈及四次及以上的高次代数方程的数值解, 故没有去求解一元四次及以上的代数方程[24]。在代数方程理论中, 一般五次及以上的代数方程更是没有根式解。原著和译著没有讨论对于一般四次及以上代数方程的解问题, 不过提及了四次及以上代数方程根式解是代数学方程理论中较复杂的问题[28]。因为对于高次代数方程数值解涉及到了根式可解性理论, 故而李善兰的数学水平没有达到这个层面上。而关于高次方程的根式解问题, 则未进行论述。代数表示理论, 《代数学》中采用的是传统数学的表示系统, 特别是各种代数式演算和变化之理。数式x的n次方, 记为天卯。《代数学》中对一些代数表达式进行了详细的分门别类, 关于代数式的分类则可以按照如下进行分类, 分为代数式和超越式, 其中的代数式分为有比例式和无比例式, 有比例式分为整式和分式, 整式就是多项式; 无比例式包括整式和分式; 其中的超越式包括指数式、对数式、圆式、反圆式等。“依数学中之除法, 用二式立之去左。[3]”其实就是一种在修辞代数下的短除法[27]。二项式展开理论, 给出了一般二项式(a+b)n的无穷展开表达式。李善兰指出最重要的是给出了二项式定理展开式中各项系数之间的关系, 并且强调其具有一般性的结果[19]。李善兰的传统数学理论中已经有二项式展开的内容, 其在幂级数理论中, 将二次方根展开为幂级数实际上就是二项式的展开理论, 并且给出了几个函数的幂级数展开式。极限及其求解理论, 《代数学》中主要是研究形如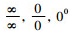
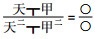
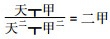
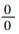
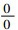
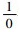
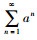
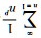
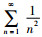
|
|
表 1 《代数学》目录 Tab. 1 Contents of Daishu Xue |
李善兰和伟烈亚力合译的《代数学》是首次传入我国的符号代数学著作。从译著可以看出在翻译西方符号代数学的过程中, 李善兰受到了中国传统代数学思想的影响[26-28]。这一点不仅是出现在《代数学》中, 在其合译的西方近代数学著作中都有体现。而李善兰本身就对中国传统代数学及其思想有过深入的研究, 有的是在其传播西方近代数学之前, 有的是在西方数学翻译之后的研究结果[29-37]。
李善兰对方程理论的论述, 中国传统代数学中很早就有对方程求解的理论, 并且“方程”一词非李善兰首创。《九章算术》第8卷“方程”中, 对方程给出了的代数学解释。杨辉在《详解九章算法》中给出了这样的解释“方者, 数之形也”。实际上, “方程”的含义实际上等同于现代意义上的线性方程组的增广矩阵。程大位(1533—1606)在《算法统宗》(1592)第8章“方程”中对方程的解释是“方, 正也; 程, 数也。”可以看出程大位对方程一词真实代数学意义的理解是不全面的。梅文鼎(1633—1721)、梅瑴成(1681—1764)都给出了相关的解读。[28]”其认为这是一种代数式的建立和代数式的运算。李善兰与伟烈亚力将“equation”译为“方程”无疑是因李善兰受到了中国传统代数学思想的影响以及伟烈亚力从西方符号代数理论中对“equation”的理解[28]。根据“equation”在Algebra中的表述, 其表示的整个代数运算式子称为方程。李善兰和伟烈亚力共同给出了方程一个定义描述“并代数之几数名为式, 二式之间作=号, 谓之方程。[3]”中国传统数学中关于方程理论有着较深入的研究, 中国传统数学中的代数方程主要是高次方程的数值解, 或者是高次联立方程组的数值解。当然, 中国传统数学中也有关于同余方程求解的问题。给出了一次同余方程:
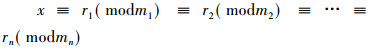
|
同时,还给出了一次同余式组的解法, 即演纪术和大衍术, 大衍术就是我们熟悉的“中国剩余定理”。这里的“中国剩余定理”是中国古代解决不定方程创造出来的一种特殊方法。特别是在历法中确定上元积年, 则要用到同余方程。上元积年是一个时刻, 则确定这个时刻就需要求解一系列的同余方程。这些同余方程, 用演纪术和大衍术都可以解决, 而对于演纪术来说更为实用。
中国传统代数学理论中建立代数方程方面, 主要是天元术, 天元术是建设代数方程的一种传统数学方法。中国传统代数学中关于解方程方面, 有增乘开方法, 即高次方程数值解。如果对于多元高次方程求解问题则发展到了四元术, 四元术则是高次多项式方程组消元法。在历法计算中, 通常情况下, 计算弧很困难, 而计算弦则要简单, 所以历算家往往就是通过一种把弦和弧进行换算。《授时历》(1280)中出现的弧矢割圆, 图 3所示⊙O中, 就是把弦和弧之间进行转化, 而建立四次方程的思想。通过建立四次方程, 并且求解四次方程, 来解决历法中所需要处理的问题。这过程中就出现了高次方程的求解问题, 关于高次方程的出现就给数学家提出了寻找解决一般高次方程的解法。
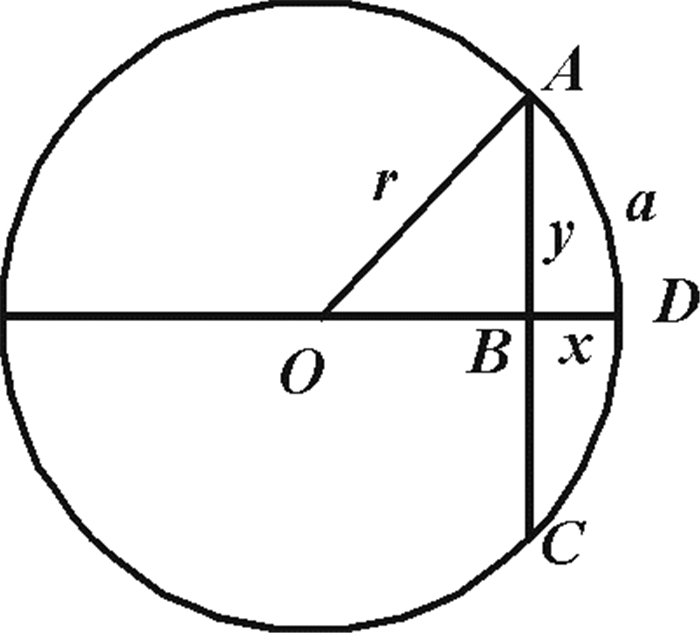
|
图 3 弧矢割圆 Fig. 3 Hu Shi Ge Yuan |
首先用天元术建立代数方程, 设半径OA=r, 半弦AB=y, 矢BD=x, 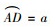
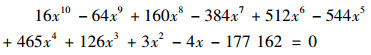
|
解得x=3, 乘以4得12, 即为平数。朱世杰用天元术建立方程, 然后用增乘开方法解方程的根。《四元玉鉴》(1303)就是用增乘开方法和四元术解决代数方程的求解问题中国传统代数学之经典著作。中国古代数学家不太在意代数方程的根式解, 而是强调代数方程数值解的值。中国传统数学中建立代数方程的天元术和代数方程数值解的增乘开方法是为了满足历法的需要而创造出来的, 而多元高次联立方程组解法的四元术则是数学家朱世杰的数学创造, 不再是为了历法的需要而创造出来的, 而是属于纯粹代数学的范畴。中国传统代数中也不关心丢番图分析, 即多元高次方程组的求解, 当然中国传统代数学中也给出了少数的几个不定方程的求解, 如给出的直角三角形中三边的平方和关系等, 给出的解就是整勾股数, 这就是简单的丢番图分析。《代数学》中同样也是给出了简单的几个丢番图方程, 但不是《代数学》关注的内容, 其主要是研究一元代数方程和其求根公式。《代数学》中的代数方程思想来于中国传统代数中的方程思想, 在求解的过程中利用了中国传统的代数学表示系统。
李善兰对代数表示理论的论述, 与西方符号代数表示相比有着独特的表示方法。方程理论是中国传统代数学最核心的内容, 而中国传统代数学中的代数表示理论则以天元术为标志, 就是设立未知数求解一元高次代数方程的数值解法。朱世杰将其推广为四元术[27]。四元高次方程组代表了当时世界上最高的代数方法求解理论水平。朱世杰的这种系统的算法被当代著名数学家吴文俊先生直接继承和发展成为著名的数学机械化思想, 也就是机械化证明的代数学基础。17世纪末, 西方传教士将一种半符号化高次代数方程根式解的方法“借根方”带到中国。然而, 后来借根方基本上被天元术所取代。《代数学》中的运算符号表示系统也是来源中国传统代数学中的古典表示系统。《代数学》中的运算符号及其表示系统来源于中国传统代数学中的古典符号及其表示系统。当然, 有的也是李善兰的一种数学创造, 李善兰在这方面创出出了很多优秀的结果和表示方法。如表示一个多项式除法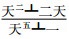

|
图 4 代数运算图 Fig. 4 Chart of algebraic operations |
从图 4中演算过程可以得到结果为
李善兰对二项式展开理论的论述, 二项式定理(Binomial theorem)又称牛顿二项式定理, 牛顿给出了两个数之和的整数次幂展开为多项式之和的代数恒等式[25]。《代数学》中的二项式定理可以推广到任意实数次幂的广义二项式定理。对二项式定理的研究关键是展开表达式及其系数, 二项式(a+b)n的展开式为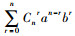
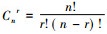
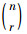
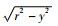
李善兰对极限理论的论述, 极限理论本来应该属于分析学的范畴, 《代数学》中将其列入, 主要是因为极限过程中的这种无穷分析求和思想, 以及在这个过程中出现的极限表达式都是通过代数式来进行表达的。极限求和思想在我国传统数学中有较早的历史, 《庄子·天下篇》中的“一尺之棰, 日取其半, 万世不竭”就是一种简单的极限思想。刘徽和祖冲之对极限思想进行了深入的发展和研究, 并且得到了一些重要的研究结果, 比如徽率、约率、密率等。李善兰给出了一种“尖锥术”的无限求和的数学方法, 李善兰根据这一无限分割求和思想揭示了点、长度、面积、体积的之间的关系, 其认为前者是后者的单位微元, 即最小元素。点就是线的单位微元, 线就是面积的单位微元, 同理, 面积就是体积的单位微元[35]。这里的“微元”相当于微积分中的dx微分微元, 这种“微元”求和思想等价于西方微积分理论中的无穷小分析, 即微分和积分理论。这是李善兰发展了中国传统数学家的理论和自己的创造得出的成果。
李善兰对级数理论的论述, 与极限理论一样都是因为在级数展开过程中出现了复杂的代数式。中国传统数学中的内插法与级数求和有关。中国传统数学中的招差术即就是内插法, 招差术的发展与中国数理天文学的发展有相关的联系。
隋代数学家、天文学家刘焯(544—610)在《皇极历》(600)中给出了招差公式, 给即就是给出了等间距二次内插法, 这一方法是中国首次得到。唐代数学家、天文学家张遂(673—727)在《大衍历》(721)中得到了不等间距二次内插公式。从宋代以后, 由于数学家对高阶等差级数进行深入的研究, 招差法得到了新的进展。元代郭守敬等历法家在《授时历》(1280)中就利用三次差的招差公式解决历法中的算法问题。在天文历法中, 通过观测得到一些天文数据, 确定一些量的关系, 如表 2中给出一些数据, 通过研究不难发现表 2中, 郭守敬给出了一种三次内插法, 即给出了一个三次内插公式, 其中的数据是通过观测得到的一些观测数据, 通过这些观测数据构造一个非常复杂的三次内插函数f(x), 其中的Δ是差分, f(x)则是求和。
|
|
表 2 三次内插法 Tab. 2 Three interpolation method |
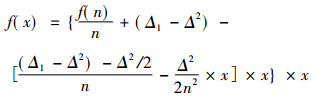
|
朱世杰在其《四元玉鉴》中给出了一个“立方招兵”的数学问题, 每天招兵人数如表 3所示。通过表 3给出的数据可以得出朱世杰事实上给出了四次招差法。朱世杰给出的招差公式只限于四次招差, 而朱世杰已经得到了其中各项系数是一系列三角垛①的积的原理, 这可以认为他已通晓了任意高次的招差法。招差, 就是差分, 通过招差法可以得出正切函数表。由于中国传统数学中没有符号代数学进行符号表述, 对于数学公式都是用传统的文字语言叙述, 这对代数学发展带来了很大的局限性。后来, 朱世杰对于这类插值问题作了更深入的研究。他在其《四元玉鉴》中成功地把高阶等差级数求和方面的研究成果运用于内插法后得到了一般的插值公式, 还明确指出公式中各项系数恰好是p=1, 2, 3, …时的三角垛求和公式。朱世杰给出了一个“立方招兵”的问题, 朱世杰从表 3中的关系给出了一个求和公式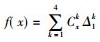
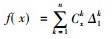
|
|
表 3 立方招兵 Tab. 3 Cubic recruiting soldiers |
① 垛积是一种高阶等差数列求和。中国古代曾经使用垛积来解对数、矩阵甚至简单的微积分。李善兰对此有较深的研究。李善兰所著《垛积比类》(1867)是一部中国特色的垛积问题研究专著, 其内容主要是关于高阶等差级数求和。给出了一个组合恒等式: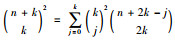
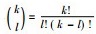
《代数学》中的级数理论, 给出了“界说, 无穷级数之总数即诸级递加递近之限。若有此限, 则谓之敛级数, 任并其诸级不能得大于限之数。若无此限, 则谓之发级数。[5]”李善兰很形象地把收敛级数命名为“敛级数”, 同时, 把发散级数命名为“散级数”。李善兰对级数的理解是《代数学》中最独到和到位的理论之一, 他从级数的本质出发指出了要搞清楚无穷级数的性质关键在于弄清楚前一项与后一项之间的递推关系, 重点解释了不能用有限项去探究或者得出无穷级数的性质与结论[35]。李善兰不仅去讨论级数的敛散性, 还研究了级数的收敛值。这一点来自于李善兰利用尖堆术将函数展开为幂级数的方法[38-40]。李善兰获得这些成果是在其翻译《代数学》之前, 故而李善兰对级数理论的翻译有着深厚的理论基础。李善兰在级数方面的重要成就体现在三个方面:一是从求平面圆的面积问题得出的一个关于圆周率的无穷级数展开代数式, 采用的尖锥术则是运用了“分离元数”的方法来归纳出一个二项式的幂级数无穷展开式; 二是求三角函数与反三角函数的幂级数无穷展开式, 就是将普通的三角函数与反三角函数无穷展开成为幂级数; 三是研究了对数函数幂级数的展开式, 得出对数函数的幂级数无穷展开。正是李善兰的这些重要的传统数学研究成果, 才使得李善兰在传播西方级数理论的时候表现非常的到位, 同时, 还能发表了更高的看法和对级数更多的研究结果。李善兰的级数理论是对中国历代数学家和历算家的级数研究成果的继承和发展, 是传统数学实际应用和理论发展的结果。
《代数学》中关于建立和求解方程、代数表示、二项式定理、极限和级数理论的论述, 都是受到了中国传统代数学思想的影响, 而且中国传统代数学理论中对这几方面的研究都有一定的广度和深度。中国传统代数学的发展是为了满足历法计算的需要, 或者是相关生活生产应用问题的需要。而有的则不是历法计算的需要, 而是数学家为了数学而数学的创造。特别是秦九韶、李冶、杨辉和朱世杰在传统代数学方面有高水平的研究成果, 宋元四大家在代数学方面的研究和成就深深地影响着中国后来传统代数学的发展和理论研究。中国传统代数学思想对《代数学》在逻辑结构、代数表示、语言模式等方面都有着很深刻的影响。后来的译著《代数术》在语言模式、代数表示和逻辑结构都受到了《代数学》的影响。创刊于1872年的《中西闻见录》(The Peking Magazine)中就有对素数判定、代数学史、天元术、勾股术、四元术等相关理论的研究[29-31]。创刊于1876年, 中国出版的较专业的科学技术期刊《格致汇编》(The Chinese Scientific Magazine)中对代数学中勾股术、开方术、解方程和极限等内容有所介绍和研究。在《中西闻见录》和《格致汇编》中的一些研究已经达到了较高的学术水平, 并且开创了数学家通过在期刊上发表论文的形式介绍最新的学术成果, 以及通过数学研究者之间进行的相互交流的重要学术研究活动[27-32]。《中西闻见录》中发表的西方符号代数学历史是传教士较早传播西方符号代数的学术记录, 而中算家在其发表的文章则是较早以学术论文形式发表的传统代数学成果, 这些成果都是受到了1859年李善兰和伟烈亚力合译《代数学》的影响。在现代数学理论的观点下去看《代数学》是比较容易的, 但是从数学思想和数学基础去研究, 却有一定的难度[41-42]。其发展的思想更为重要, 数学思想是数学发展的基石。正如吴文俊院士指出古证复原应该遵循以史实史料为依据, 不能凭空捏造, 符合本地区数学发展的实际情况, 而不能套用其他地区的或者是现代的成果, 结果应该是自然推导出来, 而不是为了达到最后的结论以致出现不合理的人为附会[43]。传统数学思想中蕴含着现代数学的理论基础, 现代数学理论中传承着传统数学思想[44-45]。从数学史研究的原则和意义来看, 《代数学》不仅是引进了西方符号代数, 而且其中蕴含着丰富的传统代数学思想。所以,只有在中国传统代数学理论体系下来看《代数学》引入西方符号代数意义,才能体现出其数学史价值,同时,也才更加科学。
4 结语中国传统代数学理论是中国传统数学理论中最为发达的一个分支, 中国传统数学的核心就是解方程。传统代数学中的方程理论来源之一就是生活生产中的应用问题, 如《九章算术》中关于代数方程的求解等; 另一方面, 则是来源于测量和几何, 如中国数理天文学中的弧矢割圆产生的四次代数方程等。代数方程理论在中国传统代数学中得到了高度的发展, 甚至发展到了多元高次联立方程组的解等问题, 是中国传统代数学发展的最高水平。
李善兰和伟烈亚力合译著作《代数学》将西方符号代数学第一次传入我国, 其中给出了一元一次、二次方程的解法, 提及到了一元三次方程的求解过程及其历史, 但是四次及其以上均未涉及, 同时, 《代数学》给出了一元二次方程的求根公式, 还讨论了根与系数的关系。虽然中国很早就有了解代数方程的理论, 并且在天文历法中隐约给出了一元二次方程的求根公式, 但是却没有给出系统的解法, 并且中国传统代数中从未关注根的存在和根与系数之间关系的问题。在《代数学》中, 李善兰运用了中国传统代数学中的天干地支等符号体系进行理论表示, 也说明当时对西方符号代数学不完全接受的态度。更重要的是当时中国的数学是中国传统文化下的数学体系。从表示系统上来看, 同样也可以看出接受的西方符号代数学是一种半符号化代数学。
中国传统数学对二项式定理有着深入的研究, 从杨辉及以后的历代数学家均给出了精彩的结果, 其中特别是李善兰在二项式定理展开理论有自己的独特的研究成果, 这些成果是来自中国传统代数学思想对李善兰的影响。因而, 李善兰在《代数学》中没有对二项式定理进行太多的论述。中国传统数学中的极限思想有着悠久的历史, 然而却没有给出一个严格的定义。《代数学》中给出了极限的定义, 并且解决了几种特殊形式的极限求法。《代数学》中讨论了级数的敛散性质, 指出了级数研究的核心内容是判断级数的敛散性, 而中国传统数学中对级数理论有着深入的研究。特别是李善兰在幂级数展开方面取得了丰厚的成果, 李善兰用尖锥术将二次方的幂级数展开就得到一些无限求和。李善兰及其清末数学家们在这一研究领域都获得了较高的学术成就。
西方符号代数学传入的主要内容与中国传统代数学有着一定的联系和区别, 其中这些理论在中国传统代数学中都能够找到。虽然中国传统代数学中对一些概念却没有严格的定义, 但是对一些代数学内容的研究, 中国传统代数则比《代数学》中的论述更为深入。可以看出《代数学》的传入给中国传统代数学带来了系统性的数学体系和符号化的表示结构, 同时, 中国传统代数学理论则成为符号代数学的理论根源。《代数学》中的表示系统和语言系统则是采用了中国传统数学的语言模式, 逻辑推理也是来自于中国传统代数学思想之中。从科学史角度来看, 《代数学》首次引进了西方符号代数学内容体系, 在中国传统代数学思想影响下进行的一次西方符号代数学传播, 是一次半符号化的数学传播, 《代数学》的出版使我国传统代数学的发展更具有科学性和系统性, 为后来中国传统代数学的完全西化作了重要铺垫。
| [1] |
MORGAN D A. Elements of Algebra[M]. London: Elibron Classics series, Adamant Media Corporation, 2003.
|
| [2] |
SMITH D E. History of Mathematics[M]. New York: Dover Publications, 1923.
|
| [3] |
德摩根.代数学[M].伟烈亚力, 李善兰, 译.上海: 墨海书馆, 1859.
|
| [4] |
曲安京. 中国数学史研究范式的转换[J]. 中国科技史杂志, 2005, 26(1): 50-58. DOI:10.3969/j.issn.1673-1441.2005.01.008 |
| [5] |
吴文俊. 中国数学史的新研究[J]. 自然杂志, 1988, 12(7): 546-551. |
| [6] |
沈康身. 中算导论[M]. 上海: 上海教育出版社, 1986.
|
| [7] |
钱宝琮. 中国数学史[M]. 北京: 科学出版社, 1964.
|
| [8] |
丘成桐. 清末与日本明治维新时期数学人才引进之比较[J]. 西北大学学报(自然科学版), 2009, 39(5): 721-725. |
| [9] |
郭书春. 中国科学技术典籍通汇数学卷[M]. 郑州: 河南教育出版社, 1993.
|
| [10] |
华罗庚. 从祖冲之的圆周率谈起[M]. 北京: 人民教育出版社, 1979.
|
| [11] |
曲安京. 中国古代的二次求根公式与反函数[J]. 西北大学学报(自然科学版), 1997, 27(1): 1-3. |
| [12] |
李继闵. 《九章算术》及刘徽注研究[M]. 西安: 陕西人民教育出版社, 1990.
|
| [13] |
李文林. 数学史概论[M]. 北京: 高等教育出版社, 2002.
|
| [14] |
曲安京. 祖冲之是如何得到圆周率π=355/113的[J]. 自然辩证法通讯, 2002, 24(3): 72-77. DOI:10.3969/j.issn.1000-0763.2002.03.021 |
| [15] |
戴念祖. 中国物理学史大系声学史[M]. 长沙: 湖南教育出版社, 2001.
|
| [16] |
吴南薰. 律学会通[M]. 北京: 科学出版社, 1964.
|
| [17] |
CHEN C Y. Acoustics in Ancient And The Sixteenth Century China[M]. Hong Kong: Hong Kong University Press, 1996.
|
| [18] |
龚镇雄. 音乐声学[M]. 北京: 电子工业出版社, 1995.
|
| [19] |
张吉良. 中国古代筹算二进制数表和《周易》[J]. 周易研究, 1988, 2(2): 67-84. |
| [20] |
谭晓春. 太极代数[J]. 周易研究, 1992, 11(1): 57-65. |
| [21] |
王俊龙. 今本《周易》卦序结构及其演绎[J]. 苏州大学学报(哲学社会科学版), 2014, 37(2): 49-56. |
| [22] |
傅熙如. 用易之乾卦来表达的奇素数集[J]. 周易研究, 1998, 36(2): 88-93. |
| [23] |
陈玲. 《周易》与中国传统数学[J]. 厦门大学学报(哲学社会科学版), 2014, 222(2): 66-72. |
| [24] |
刘大钧. 大易集释[M]. 上海: 上海古籍出版社, 2007.
|
| [25] |
冯友兰. 中国哲学史新编[M]. 北京: 人民出版社, 1998.
|
| [26] |
白寿彝. 中国通史[M]. 上海: 上海人民出版社, 1999.
|
| [27] |
张必胜.《代数学》和《代微积拾级》研究[D].西安: 西北大学, 2013.
|
| [28] |
张必胜. 李善兰与伟烈亚力合译《代数学》的主要内容研究[J]. 西北大学学报(自然科学版), 2013, 43(6): 1021-1026. |
| [29] |
张必胜. 《中西闻见录》及其西方科学技术知识传播探析[J]. 贵州社会科学, 2012, 272(8): 25-27. DOI:10.3969/j.issn.1002-6924.2012.08.004 |
| [30] |
张必胜, 姚远. 《中西闻见录》与其数学传播[J]. 西北大学学报(自然科学版), 2011, 41(5): 935-940. |
| [31] |
张必胜. 李善兰考数根法的研究[J]. 贵州大学学报(自然科学版), 2011, 28(2): 1-5. DOI:10.3969/j.issn.1000-5269.2011.02.001 |
| [32] |
张必胜. 《中西闻见录》中的科学技术知识分析[J]. 贵州大学学报(自然科学版), 2017, 34(1): 1-9. |
| [33] |
张必胜. 《代微积拾级》的主要内容研究[J]. 西北大学学报(自然科学版), 2016, 46(6): 923-931. |
| [34] |
张必胜. 李善兰微积分思想研究[J]. 贵州大学学报(自然科学版), 2013, 30(6): 1-5. DOI:10.3969/j.issn.1000-5269.2013.06.001 |
| [35] |
张必胜, 袁权龙. 李善兰极限思想研究[J]. 贵州大学学报(自然科学版), 2015, 32(3): 7-9. |
| [36] |
张必胜. 李善兰组合思想研究[J]. 贵州大学学报(自然科学版), 2016, 33(1): 5-8. |
| [37] |
徐光慧, 任定成. 《则古昔斋算学》数学语言系统初探[J]. 自然辩证法研究, 2015, 31(7): 91-97. |
| [38] |
李俨. 三十年来之中国算学史[J]. 科学, 1947, 29(4): 101-108. |
| [39] |
徐传胜. 中国传统代数学思想对幂级数理论的研究[J]. 西安电子科技大学学报(社会科学版), 2006, 16(2): 143-148. DOI:10.3969/j.issn.1008-472X.2006.02.029 |
| [40] |
王渝生. 李善兰的尖锥术[J]. 自然科学史研究, 1983, 2(3): 266-288. |
| [41] |
林群, 刘嘉荃. 从圆周率计算到有限元外推技术[J]. 数学的实践与认识, 1989, 19(4): 62-72. |
| [42] |
张景中, 冯勇. 微积分基础的新视角[J]. 中国科学A辑:数学, 2009, 39(2): 247-256. |
| [43] |
吴文俊. 古证复原的原则[J]. 世界科学, 1981, 3(10): 56. |
| [44] |
齐民友. 从积分概念的发展看数学分析基本概念的发展[J]. 高等数学研究, 2014, 17(1): 6-16. DOI:10.3969/j.issn.1008-1399.2014.01.002 |
| [45] |
曲安京. 中国古代数理天文学中的数值计算方法[J]. 西北大学学报(自然科学版), 1998, 28(2): 99-104. |
 2017, Vol. 47
2017, Vol. 47