2. 北京师范大学 信息科学与技术学院, 北京 100875
2. College of Information Science and Technology, Beijing Normal University, Beijing 100875, China
地球上现存35万多种高等植物和31万未知植物物种, 任何人包括植物学家都不能很容易识别这些物种。因此, 利用计算机辅助识别植物种类必然成为未来趋势。
根据叶片识别植物是一种直接有效的方法, 特征表示性能和分类器的选取直接影响分类效果。在特征提取方面, Harish[1], Wu[2], Kulkarni[3]及Kadir[4]提出利用数字几何特征描述叶轮廓、纹理等信息, 并在Flavia数据集上进行测试, 最高正确率可达到93.82%;然而提取轮廓线[1-6]时不可避免地存在各种误差, 导致特征表示性能降低。因此, Sfar[7]和Hu[8]提出利用对象相似性和后验概率提升表示性能。分类器选取方面, 概率神经网络(PNN)[9-10]和支持向量机(SVM)[10-11]是最常用的分类器, Du[6]和Zhang[12]提出移动平均超球面和SVM+KNN融合处理多分类问题。
传统方法不能很好地表示左右不对称和弯曲叶片的特征, 针对该问题借鉴SPM(Spatial pyramid matching)[13]分层思想, 将图像均等分割, 提取各个空间子区域的高阶Zernike矩特征, 提出使用滑动圆形窗口识别对象域, 并基于该对象域提取极坐标傅里叶描述子, 将Zernike矩[14]和极坐标傅里叶特征[15]作为深度神经网络[16]的输入层向量, 进一步提取优化后的深度抽象特征, 在多个经典数据集随机选取不同比例的训练集和测试集, 与多种经典特征提取方法进行比较, 实验结果表明, 该方法提取的特征能够较好地表示对象。
1 理论基础 1.1 Zernike矩Zernike[17]是多项式的正交化函数, 该特征具有旋转不变性和较小数据冗余等优势。但其特征值仅满足旋转不变性, 当采用Zernike矩作为形状描述子时, 须对其进行归一化, 使其满足平移和尺度不变性。因此, 文中将归一化后的高阶Zernike矩作为特征描述子。
设图像函数为I=f(x, y), Zernike矩多项表达式{Zpq(x, y)}[17]为
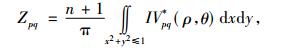
|
(1) |
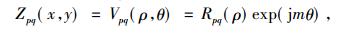
|
(2) |
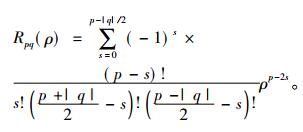
|
(3) |
其中, p为阶数, q为重复率, p-|q|是偶数, 且p≥q, Vpq(x, y)为复数函数, ρ表示原点到点(x, y)的矢量长度, θ表示这个矢量与x轴逆时针方向的夹角, Rpq(ρ)为点(x, y)径向多项式。
单位圆内的任何图像f(x, y)都可以用式(4)表示,
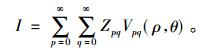
|
(4) |
将图像质心看作原点, 并将像素坐标投射到单位圆内, 如果x2+y2≤1, 统计单位圆内的像素点数。
1.2 极坐标傅里叶变换PFT特征能较好地描述目标形状和环状特征, 且抗干扰能力强, 通用性高。因此, 文中选用Kadir[10]提出的PFT特征表示图像, 该特征满足RST不变性。可描述为
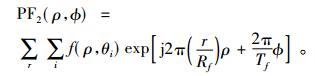
|
(5) |
其中, 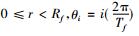
设图像I={f(x, y); 0≤x < M, 0≤y < N}, 将图像投射到极坐标Ip={f(r, θ); 0≤r < Rmax, 0≤θ < 2π}上, Rmax为图像轮廓质心到轮廓线的最大半径。图像质心坐标(xc, yc)为
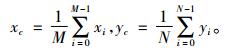
|
(6) |
r和θ表达式为
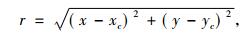
|
(7) |
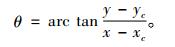
|
(8) |
为了实现PFT的尺度不变性, 对Ip进行傅里叶变换, 得到变换系数数列PF, 采用式(9)归一化表示,
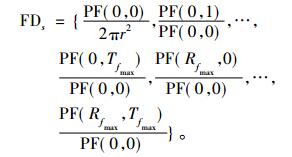
|
(9) |
其中, Rfmax是径向频率最大值, Tfmax是三角频率最大值。
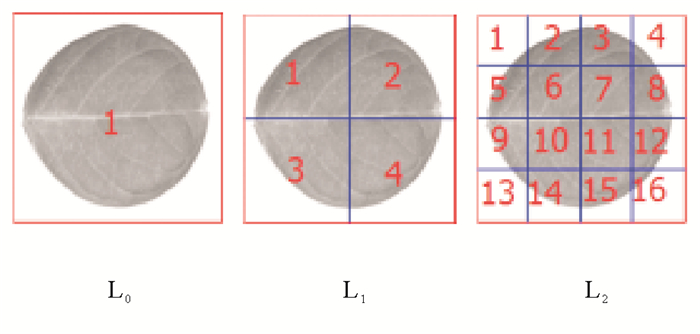
2 MSF方法MSF(Multi-scale features)方法首先对预处理后的图像利用SPM分层策略均等分割, 如图 1所示, 提取L0, L1, L2层的高阶Zernike矩特征, 利用滑动圆形窗口检测对象区域, 基于对象域提取PFTD特征; 其次, 将L0, L1, L2层的Zernike矩特征和PFTD特征作为DNN输入层向量, 获取深度网络抽象特征集; 最后利用概率SVM分类器实现植物分类。
|
图 1 SPM示意图 Fig. 1 The diagram of spatial pyramid matching |
采用灰度化、高斯滤波和形态学滤波对叶片进行预处理。
1) 灰度化。叶片颜色因时间、环境等不可忽略的外部因素产生变化, 直接影响识别效果。因此, 须对彩色图像进行灰度化处理。统计每个像素点的灰度值[6]
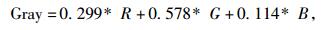
|
(10) |
2) 高斯滤波。由于数字图像在采集过程中易受外界噪声干扰, 采用高斯滤波算法消除离散噪声。
3) 形态学滤波。对去噪后图像利用形态学的开闭运算, 一定程度上对缺损叶片进行了修复。
2.2 特征提取 2.2.1 Zernike矩L0, L1, L2层的2~13的高阶Zernike矩特征分别表示为:
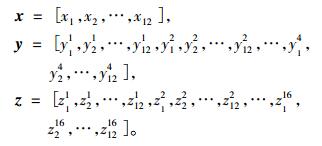
|
其中, yi=[y1i, y2i, …, y12i], i=1, 2, 3, 4, 表示L1层第i个空间域的12个Zernike矩特征, zj=[z1j, z2j, …, z12j](j=1, 2, …, 16)表示L2层第j个空间域的12个Zernike矩特征。
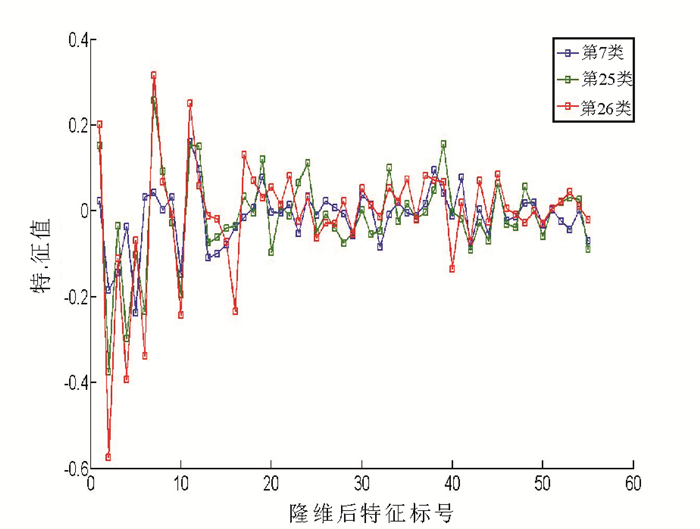
任选Flavia数据集中3类相似植物种类, 如图 2所示。图 3描述了经PCA降维后的L2层55个特征值, 贡献率设置为95%。根据图 3可知, 图 2中相似植物种类在多个等特征下具有明显区分度。

|
图 2 相似植物种类 Fig. 2 The similar plant species |
|
图 3 相似种类z特征 Fig. 3 The z value of the similar species |
文中利用自适应阈值分割算法[18]获取对象域, 将叶片长轴ll作为横坐标轴, 短轴, ls作为纵坐标轴, 对象被分割成4个域, 再利用滑动圆形窗口在各个区域提取PFTD特征, 半径r=ls/4。
据Kadir[10]实验结果可知:Rfmax=4, Tfmax=6时取得最佳分类效果, 文中也设置相同参数。在Flavia数据集上共提取400个PFTD特征。为了简化计算, 经PCA降维后维度变为31个。
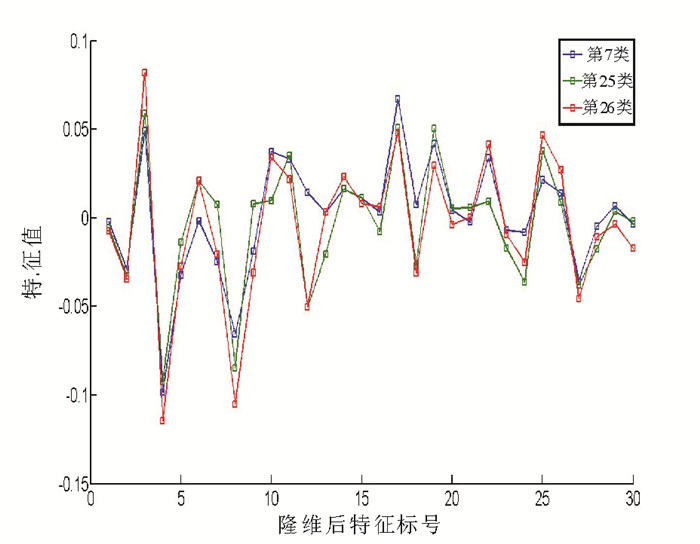
图 4为相似种类的PFTD特征值, 根据图 4可知相似种类在PFTD特征下区分度不明显, 恰与Zernike矩特征互补。
|
图 4 相似种类PFTD特征 Fig. 4 The PFTD value of the similar species |
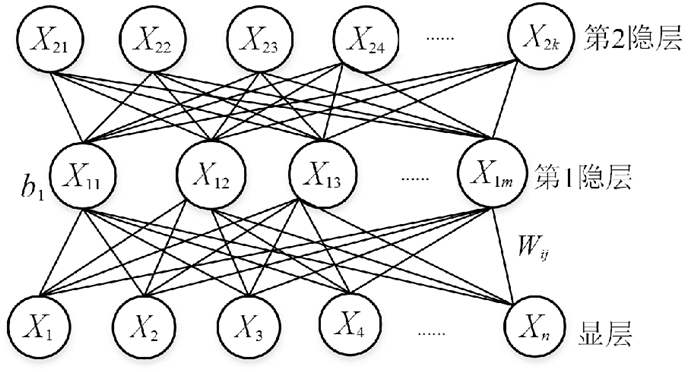
为了训练对象本质特征, 采用包含瓶颈层的DNN[19]进行特征优化, 瓶颈层包含节点数最少, 因此, 将该层节点值作为输入向量的低维表示。图 5为深度神经网络架构。
|
图 5 深度神经网络架构 Fig. 5 The architecture of the deep neural network |
文中将每幅图像多尺度下的Zernike矩和PFTD特征排列成列向量xi, 所有输入的n维图像构成特征矩阵X=(x1, x2, …, xn)T, 作为DNN原始输入数据, DNN结构为1个输入层, k个隐含层和1个输出层, 第1隐含层的状态为[20]
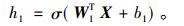
|
(11) |
其中, W1为输入层与第1隐层间神经元的链接权值, b1为第1隐层的网络偏置,
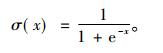
|
(12) |
对于一个由k个隐含层组成的深层网络, 采用贪婪算法逐层初始化, 求解第k/2隐层即瓶颈层的参数值,
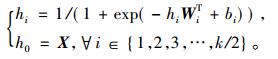
|
(13) |
根据神经网络的反向传播性质得到全局最优权值向量,
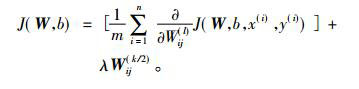
|
(14) |
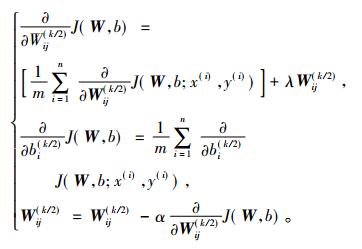
|
(15) |
其中, J(W, b)是损失函数, α是步长系数。
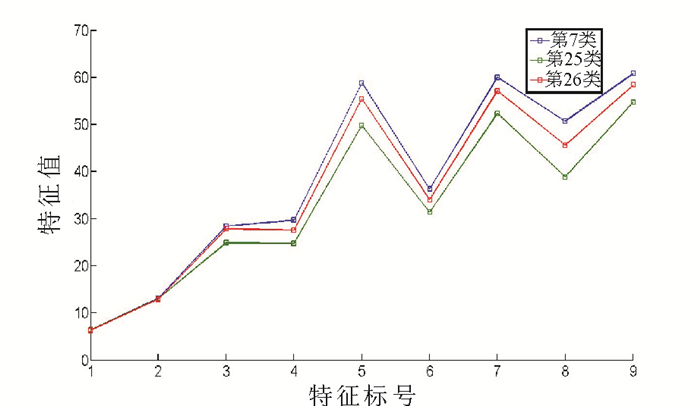
图 6描述了相似植物种类特征经DNN优化后的特征值变化, 可知优化后的特征使得特征区分度更加显著。
|
图 6 相似种类dn特征 Fig. 6 The dn value of the similar species |
由于SVM对小样本和非线性问题具有良好的适应性[18]。因此, MSF方法采用由Lin等开发的LIBSVM工具箱①。设叶片种类有k类, 多尺度特征集[x, y, z, pftd, dn], 则5个特征, k个类别的样本共需设计5k(k-1)/2个SVM分类器。其中, pftd由4个区域统计PFTD特征构成; dn由瓶颈层特征构成。
① http://www.csie.ntu.edu.tw/~cjlin/libsvm/
对某一待测样本分类时, 通过SVM获取[x, y, z, pftd, dn]各个特征对应的决策值行向量Bi*(k(k-1)/2)(i=1, 2, 3, 4, 5)。利用算法1获取所有特征[x, y, z, pftd, dn]组成的5*k概率矩阵M5*k=[C1; C2; C3; C4; C5]。Ci表示在第i个特征下待测样本属于某一类的k维向量。
算法1 决策值矩阵转化为概率矩阵算法
输入 待测样本在第i个特征下对应的k(k-1)/2维决策值行向量Bk(k-1)/2。
输出 待测样本属于某一类的k维概率行向量Ci*k。
步骤1 初始化零矩阵Bk(k-1)/2Ak*k。
步骤2 行向量按行转化为Ak*k的上三角矩阵。
步骤3 当A(i′, j′)>0, A(i′, j′)属于第i′类; 当A(i′, j′) < 0, A(i′, j′)属于第j′类。根据Ak*k统计该样本属于第q类的概率, C(q)=N(q)/(k(k-1)/2)。其中, N(q)为该样本判别为第q类的SVM子分类器数量, q=1, 2, …, k, C(q)为该样本在第i个特征下判定为q类的行向量, 执行i=i+1直到i=5结束。
对每个特征[x, y, z, pftd, dn]对应每类的概率值从大到小排序, 获取各个特征的前3个最大特征值对应的类别c(i′), i′=1, 2, …, 15, 依据c(i′)统计样本属于第q类的数量M(q), 则该待测样本类别为
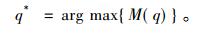
|
为了验证MSF的有效性, 采用Flavia和Swedish数据集进行测试, 与文献[8]提出的MDM算法, 以及文献[18]和[21]的算法进行实验比较。其中, Flavia数据集共包括1 907张图像大小不同及每类数量不等的32种植物种类; Swedish数据集共包括1 125张图像及每类75张图像的15种植物。
3.1 参数设置采用Libsvm工具箱自带RBF核函数的c-svm算法, 正则参数c∈{4-10, 4-9, …, 49, 410}, 核函数g∈{4-10, 4-9, …, 49, 410}, 利用枚举法获得最优分类效果最佳参数c=44与g=45。
3.2 结果对比分析实验中采用与文献[8]相同降维方法DNM[22], 并采用PCA和LDA降维方法在Flavia和Swedish数据集进行多组测试, 与文献[18]和[21]方法进行了对比, 由于文献[18]和[21]特征维度较低, 因此未对其降维处理。
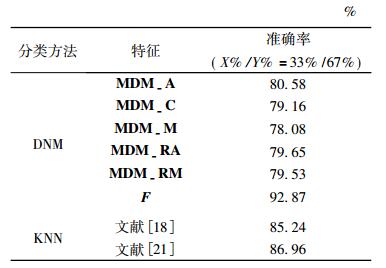
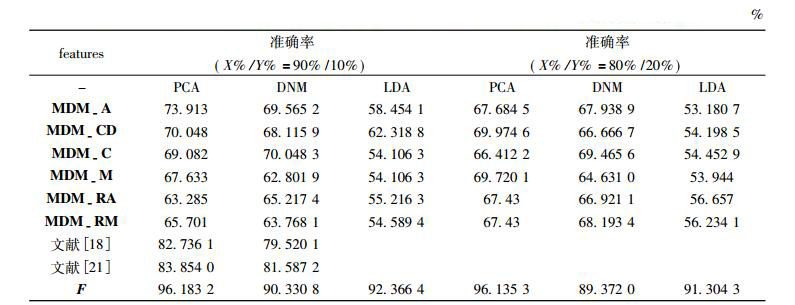
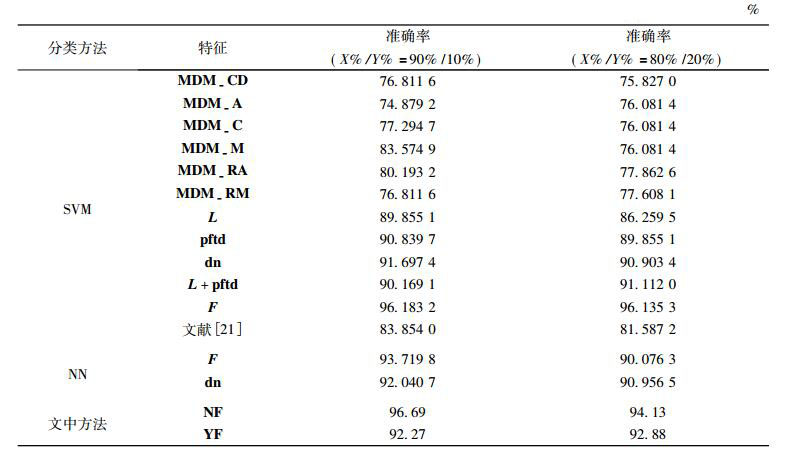
表 1中选取与Hu[11]相同比例的Swedish数据集, 使用DNM和最近邻进行分类, 文献[18]和[21]直接使用最近邻分类, X%/Y%表示随机选取X%作为训练集, 剩余Y%作为测试集, X+Y=100。表 2中随机选取不同比例的Flavia数据集, 使用PCA, DNM, LDA降维和SVM分类器进行分类; 表 3中随机选取不同比例的Flavia数据集, 均用PCA进行降维, 将SVM, NN及文中分类方法进行对比分析。其中, MDM-CD, MDM-A, MDM-C, MDM-M, MDM-RA, MDM-RM是文献[8]中距离矩阵MDM的6种扩展形式, L=[x; y; z]; F=[L, pftd, dn]; 未归一化特征为NF; 归一化特征为YF; dn表示瓶颈层特征。
|
|
表 1 Swedish数据集分类结果 Tab. 1 The classification results on the Swedish dataset |
|
|
表 2 Flavia数据集不同降维方法的SVM分类结果 Tab. 2 Results on the Flavia dataset with various dimension reduction method in the SVM classifier |
|
|
表 3 Flavia数据集使用SVM, NN及文中算法分类结果 Tab. 3 Results on the Flavia dataset with the SVM and NN and classifier in this paper |
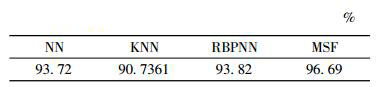
MDM算法针对左右对称和完全伸展的叶片具有较好效果, 但对于不对称及缺损叶片具有明显的局限性, 由表 1可知。表 1采用与Hu[8]相同的参数设置, 文中特征与Hu[8]所有特征相比正确率提高约12%, 与文献[8]和[21]相比提高约6%。文献[8]和[21]根据几何形态学数值计算提取特征, 对轮廓线的提取精度要求较高, 然而现存轮廓线提取算法不可避免地存在误差, 文中方法对轮廓线精度要求不高, 减少了数字几何特征对分类效果的影响。由于细粒度Zernike矩特征和PFTD特征维度过高且奇异点和噪声点严重影响分类精度。因此, 文中采取了多种降维方法, 排除噪点降维后特征分类性能获得了较好地改善, 由表 2的分类效果可知。表 3在Flavia数据集上将文中提取的神经网络优化后特征与MDM距离特征进行对比, 并利用本文设计的基于概率的SVM与其他分类器相比具有较优且鲁棒的分类效果; 表 4在Flavia数据集上随机选取90%的训练样本, 文中提取的多尺度F特征在各种分类器下进行训练分类, 从分类效果可见MSF算法针对缺损叶片和未伸展叶片具有一定优势。
|
|
表 4 Flavia数据集上MSF与其他方法分类结果 Tab. 4 Results on the Flavia dataset with MSF and other methods |
实验表明:该方法归一化后的Zernike, PFTD和DNN特征均满足RST不变性; SPM的分层策略有效地将全局特征和局部特征进行融合, 保留了更多的对象信息; 利用圆形滑动窗检测对象, 并在对象区域内提取PFTD特征, 缩小特征提取范围和计算量; 仅利用形态学特征且不需要较多的数字几何计算, 不需要考虑点对应问题, 减少了特征提取过程的时间复杂度; 与多种分类方法相比, 该方法可达到约96.69%的准确率。因此, 文中方法针对缺损叶片、弯曲叶片和左右不对称叶片也具有很好的分类效果。
4 结论针对左右不对称和弯曲叶片图像特征表示性能不佳问题, 提出了基于深度神经网络的多尺度特征提取方法。首先, 借鉴SPM分层思想将图像均等分割成多个特征层, 基于该特征层提取高阶Zernike矩特征; 利用滑动圆形窗口检测对象, 在对象域极坐标提取傅里叶描述子; Zernike矩和极坐标傅里叶描述子构成多尺度特征, 再利用深度神经网络在该多尺度特征集上提取深度抽象特征, 实验数据表明, 该特征能够较好地表示对象。下一步工作是提取不同对象特征, 提高特征表示性能, 并选用多种数据集进行实验研究。
| [1] |
HARISH B S, HEDGE A, VENKATESH O, et al.Classification of plant leaves using morrhological features and zernike moments[C]//Advances in Computing, Communications and Informatics, IEEE, 2013: 1827-1831.
|
| [2] |
WU S G, BAO F S, XU E Y, et al.A leaf recognition algorithm for plant classification using probabilistic neural network[C]//IEEE International Symposium on Signal Processing & Information Technology.IEEE, 2007: 11-16.
|
| [3] |
KULKARN A H, RAI H M, JAHAGIRDAR D K A, et al. A leaf recognition technique for plant classification using RBPNN and Zernike moments[J]. Computer-Mediated Communication, 2013, 2(1): 984-988. |
| [4] |
KADIR A, NUGROHO L E, SUSANTO A, et al. Neural network application on foliage plant identification[J]. Springer International Handbooks of Education, 2013, 11(8): 15-22. |
| [5] |
MOUINE S, YAHIAOUI I, VERROUST-BLONDET A.A shape-based approach for leaf classification using multiscale triangular representation[C]//The International Conference on Multimedia Retrieval.New York: ACM, 2013: 127-134.
|
| [6] |
DU J X, WANG X F, ZHANG G J. Leaf shape based plant species recognition[J]. Applied Mathematics & Computation, 2007, 185: 883-893. |
| [7] |
REJEB A, BOUJEMAA N, GEMAN D.Identification of plants from multiple images and botanical idkeys[C]//The International Conference on Multimedia Retrieval.New York: ACM, 2013: 191-198.
|
| [8] |
HU R X, JIA W, LING H B, et al. Multiscale distance matrix for fast plant leaf recognition[J]. IEEE Transactions on Image Processing, 2012, 21(11): 4667-4672. DOI:10.1109/TIP.2012.2207391 |
| [9] |
KADIR A, SANTOSA P I, NUGROHO L E, et al. Experiments of zernike moments for leaf identification[J]. Theoretical & Applied Information Technology, 2012, 41(1): 82-93. |
| [10] |
KADIR A, NUGROHO L E, SUSANTO A, et al. Foliage plant retrieval using polar fourier transform, color moments and vein features[J]. Signal & Image Processing, 2011, 2(3): 1-13. |
| [11] |
QUADRI A T, SIRSHAR M. Leaf recognition system using multi-class kernel support vector machine[J]. Computer and Communication System Engineering, 2015, 2(2): 260-263. |
| [12] |
ZHANG H, BERG A C, MAIRE M, et al.SVM-KNN: Discriminative nearest neighbor classification for visual category recognition[C]//IEEE Computer Society Conference on Computer Vision & Pattern Recognition.IEEE, 2006, 2: 2126-2136.
|
| [13] |
LAZEBNIK S, SCHMID C, PONCE J. Beyond bags of features:Spatial pyramid matching for recognizing natural scene categorie[J]. Computer Vision and Pattern Recognition, 2006, 2: 2169-2178. |
| [14] |
SALVE P, SARDESAI M, MANZA R, et al.Identification of the plants based on leaf shape descriptors[C]//Proceedings of the Second International Conference on Compnter and Communication Technologies.Spring India, 2016: 85-101.
|
| [15] |
KADIR A.Leaf identification using polar Fourier transform and linear Bayes normal classifier[C]//Biological Shape Analysis: Proceedings of the 3rd International Symposium, 2015: 40-49.
|
| [16] |
POVEY D, ZHANG X H, KHUDANPPUR S. Parallel training of DNNS with natural gradient and parameter averaging[J]. Eprint Arxiv, 2014, 14(10): 7455. |
| [17] |
KHOTANZAD A, HONG Y H. Invariant image recognition by Zernike moments[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1990, 12(5): 489-497. |
| [18] |
王丽君, 淮永建, 彭月橙. 基于叶片图像多特征融合的观叶植物种类识别[J]. 北京林业大学学报, 2015, 37(1): 54-61. |
| [19] |
崔瑞莲, 宋彦, 蒋兵, 等. 基于深度神经网络的语种识别[J]. 模式识别与人工智能, 2015, 28(12): 1093-1099. |
| [20] |
李帅, 许悦雷, 马时平, 等. 一种深度网络SAR遮挡目标识别方法[J]. 西安电子科技大学学报(自然科学版), 2015, 42(3): 154-160. |
| [21] |
董红霞, 郭斯羽. 一种结合形状与纹理特征的植物叶片分类方法[J]. 计算机工程与应用, 2014, 50(23): 185-188. DOI:10.3778/j.issn.1002-8331.1301-0138 |
| [22] |
JIA Y, NIE F, ZHANG C. Trace ratio problem revisited[J]. IEEE Transactions on Neural Networks, 2009, 20(4): 729-735. DOI:10.1109/TNN.2009.2015760 |
 2017, Vol. 47
2017, Vol. 47
 , 周明全1,2, 耿国华1, 刘晓宁1, 王恒1
, 周明全1,2, 耿国华1, 刘晓宁1, 王恒1