不变子空间方法是求非线性偏微分方程的精确解的有效方法, 在非线性算子允许的空间内可以构造方程的解, 已经在此方面有许多有意义的结果[1-15], 因此, 由允许的不变子空间来推出具体非线性算子是很重要的, 文献[7]分别研究了二阶非线性算子, 文献[8]研究了三阶非线性算子, 本文借助于Mapler软件推出四阶非线性算子
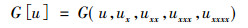
|
(1) |
允许六维多项式不变子空间的算子的表达式, 这样便于方程精确解的研究。
1 不变子空间方法对于形如
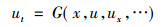
|
(2) |
的k阶非线性方程, 其中G(x, u, ux, …)对各个变量都是光滑函数。令g1(x), g2(x), …, gp(x)是线性无关, 它们的线性组合是
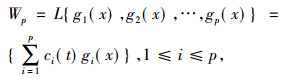
|
如果非线性算子G满足G[Wp]⊆Wp, 即, 对任意ci(t), 有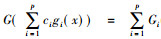
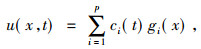
|
(3) |
将式(3)代入(2), 得出ci(t)满足
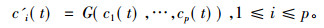
|
假设子空间Wp是由常系数常微分方程
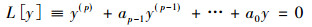
|
的解构成的, 则非线性算子G允许的空间Wp不变的条件为L[G[u]]|[H]=0, [H]表示L[u]=0及关于x的微分。
定理1[4, 9] 若线性子空间Wp在k阶微分算子G作用下不变, 则p≤2k+1。
2 主要结果对于四阶非线性算子
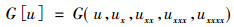
|
根据定理1知, 它允许九维以下的子空间, 但考虑到计算量很大, 本文只讨论六维不变子空间, 在
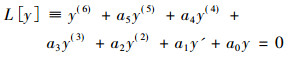
|
中令a5=a4=a3=a2=a1=a0=0, 即L[y]≡y(6)=0的解, 构成不变子空间
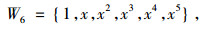
|
在W6中算子式(1)有变量分离形式解
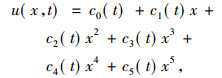
|
那么四阶非线性算子(1)具有咋样的形式?由不变子空间方法及不变条件
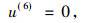
|
(4) |
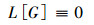
|
(5) |
得出下面的结论。
定理2 四阶非线性算子式(1)允许六维多项式不变子空间W6={1, x, x2, x3, x4, x5}时, 四阶非线性算子的表达式为
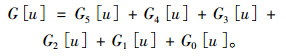
|
其中
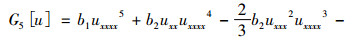
|
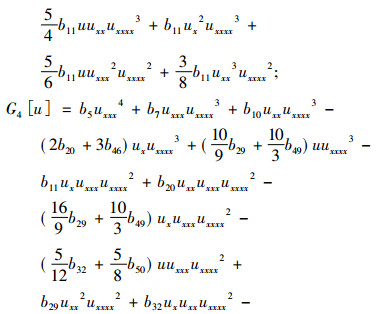
|
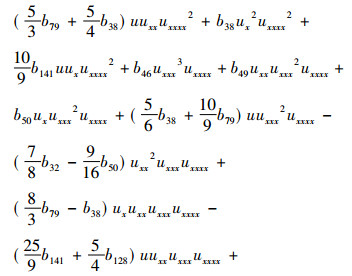
|
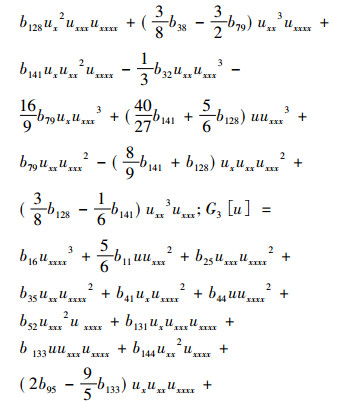
|
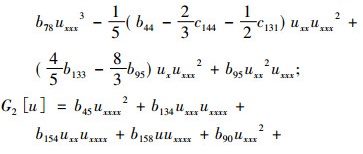
|
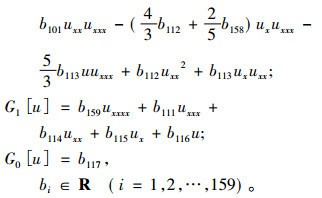
|
证 明 将式(1)(4), 代入式(5), 得出式(5)的左边是关于u偏导数乘积的和的式子, 并令它们的系数为零, 从而得出(uxxxxx)6的系数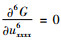
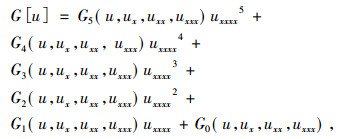
|
(6) |
将式(4),(6)代入式(5), 得出
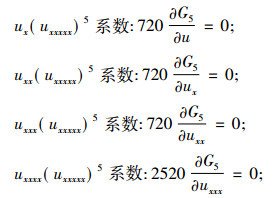
|
故有
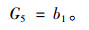
|
(7) |
由(uxxxxx)5系数: 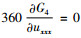
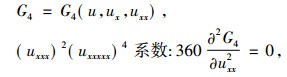
|
得出
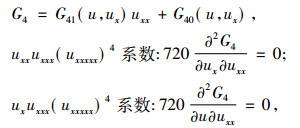
|
得出
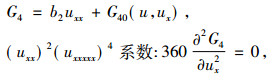
|
得出
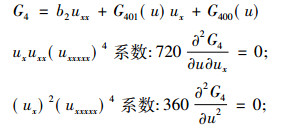
|
得出
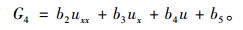
|
(8) |
将式(4),(7),(8)代入式(6),再代入式(5)得出,
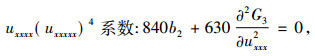
|
有
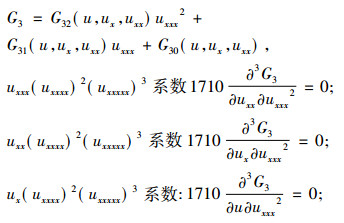
|
得出G32=b6,
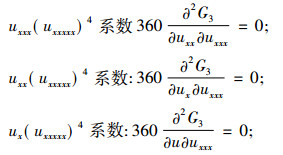
|
得出G31=b7,

|
得出
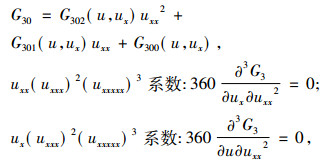
|
得出G302=b8,

|

|
得出
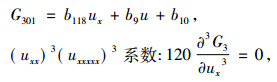
|
得出
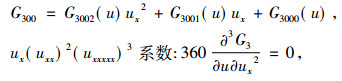
|
得出

|
得出
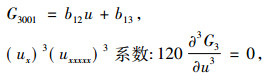
|
得出
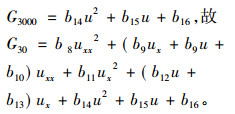
|
因此
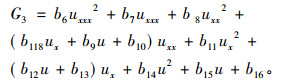
|
类似地分析计算, 得出
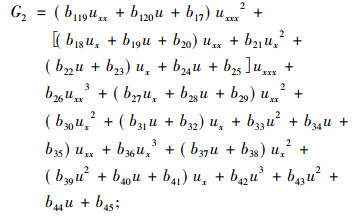
|
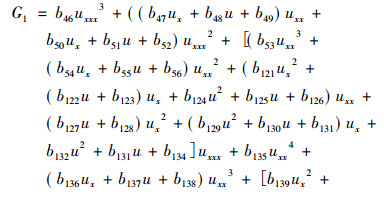
|
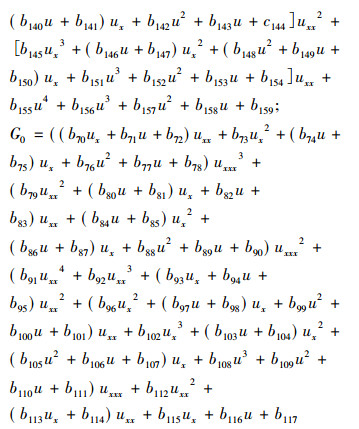
|
将G5,G4,G3,G2,G1,G0代入式(6), 再代入式(5), 整理, 并令等式左边u偏导数乘积的系数为零, 解得bi, 再回代到式(6), 即得到结果。
3 举例含有二次算子G2[u]的方程
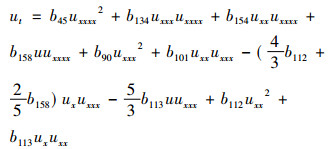
|
允许不变子空间W6={1, x, x2, x3, x4, x5}, 因此方程有解
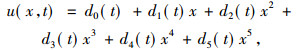
|
其中d0(t), d1(t), d2(t), d3(t), d4(t), d5(t)满足
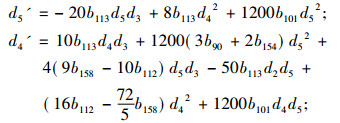
|
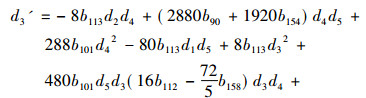
|
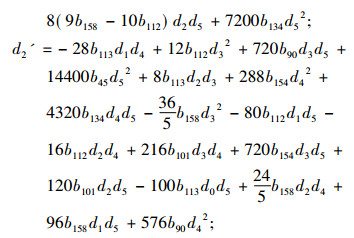
|
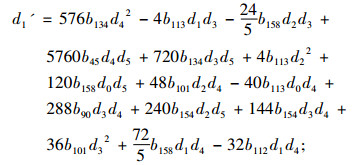
|
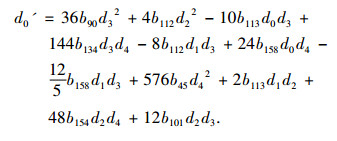
|
本文推出四阶非线性算子F允许六维多项式不变子空间时, 该四阶算子的表达式, 可以在六维多项式不变子空间上构造出方程的精确解, 同时运用本方法, 也可以推出四阶非线性算子F在允许七维、八维、九维子空间时, 算子的表达式, 并且可以在这些子空间中构造出方程更多的精确解。
| [1] |
FOKAS A S, LIU Q M. Generalized Condition symmetries and exact solutions of nonintegrable equations[J]. Theor Math Phys, 1994, 99(2): 571-582. DOI:10.1007/BF01016141 |
| [2] |
GALAKTIONOV V A. Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities[J]. Proc Roy Soc Edinburgh, Sect A, 1995, 125(2): 225-246. DOI:10.1017/S0308210500028018 |
| [3] |
QU C Z, ZHU C R. Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J]. J Phys A, 2009, 42(47): 1-27. |
| [4] |
SVIRSHCHEVSKⅡ S R. Symmetries of linear ODEs and generalized separation of variables in nonlinear equations[J]. Phys Lett A, 1995, 199(56): 344-348. |
| [5] |
MA W X. A refined invariant subspaces meth-od and applications to evolutions[J]. Sci China Math, 2012, 55(9): 1769-1778. DOI:10.1007/s11425-012-4408-9 |
| [6] |
SHEN S F, QU C Z, JIN Y Y, et al. Maximal dimensi-on of invariant subspaces to systems of nonlinear evolution equations[J]. Chinese Ann of Math B, 2012, 33(2): 161-178. DOI:10.1007/s11401-012-0705-4 |
| [7] |
ZHU C R. Second-order nonlinear differential operators possessing invariant subspaces of submaximal dimension[J]. Chin Phys B, 2011, 20(1): 010201(1)-010201(8). |
| [8] |
QU G Z, ZHANG S L, LI Y L. Third-order nonlinear differential operators preserving invariant subspaces of maximal dimension[J]. Chin Phys B, 2014, 23(11): 110202(1)-010202(7). |
| [9] |
FOKAS A S, LIU Q M. Nonlinear interaction of traveling wave of nonintegrable equations[J]. Phys Rev Lett, 1994, 72(21): 32933296. |
| [10] |
JI L N, QU C Z. Condition Lie-Bäcklund symmetry and invariant subspace to nonlinear diffusion equation[J]. IMA J Appl Math, 2011, 76(4): 610632. |
| [11] |
QU C Z, JI L N, WANG L Z. Conditional Lie-Bäcklund symmetries and sin-invariants to quasilinear diffusion equations[J]. Stud Appl Math, 2007, 119(4): 355391. |
| [12] |
GAZIZOV R K, KASATKIN A A. Construction of exact solutions for fractional order differrential equations by the invariant subspace m ethod[J]. Comput Math Appl, 2013, 66(5): 576-584. DOI:10.1016/j.camwa.2013.05.006 |
| [13] |
SONG J Q, SHEN SF, JIN Y Y, et al. New maximal dimension of invariant subspaces to coupled systems with two-component equations[J]. Commun Nonlinear Sci, 2013, 18(11): 2984-2992. DOI:10.1016/j.cnsns.2013.03.019 |
| [14] |
CHOU K S, QU C Z. Generalized conditional symmetries of nonlinear differential difference equations[J]. Phys Lett A, 2001, 280(5): 303-308. |
| [15] |
QU C Z, ZHANG S L, Liu R C. Separation of variable and exact solutions to quasilinear diffusion equations with nonlinear source[J]. Physica D, 2000, 144(1-2): 97-123. DOI:10.1016/S0167-2789(00)00069-5 |
 2017, Vol. 47
2017, Vol. 47