在本文中, H与K都表示无限维的复可分Hilbert空间, B(H, K)表示H到K上的有界线性算子的全体, 记B(H, H)=B(H), K(H)表示B(H)中紧算子的全体。int表示一个集合的内点。对算子T∈B(H), 用n(T)来表示零空间N(T)的维数, d(T)表示值域R(T)的余维数。若n(T) < ∞且R(T)闭, 称T为上半Fredholm算子; 特别地, 当n(T)=0且R(T)闭时, 称T为下有界算子。若d(T) < ∞且R(T)闭, 称T为下半Fredholm算子; 特别地, 当d(T)=0时, 称T为满算子。上半Fredholm算子和下半Fredholm算子统称为半Fredholm算子。T∈B(H)称为Fredholm算子, 若R(T)闭且n(T)和d(T)都有限。若T∈B(H)为半Fredholm算子, T的指标ind(T)定义为ind(T)=n(T)-d(T)。算子T的升标asc(T)为满足N(Tn)=N(Tn+1)的最小非负整数, 若这样的整数不存在, 则记asc(T)=+∞; 而算子T的降标des(T)为满足R(Tn)=R(Tn+1)的最小非负整数, 同样当这样的整数不存在时, 记des(T)=+∞。若T是指标为零的Fredholm算子, 称T为Weyl算子。若T为有有限升标和有限降标的Fredholm算子, 称T为Browder算子。算子T的谱σ(T), 逼近点谱σa(T), Browder谱σb(T), 半Fredholm谱σSF(T)分别定义为:
σ(T)={λ∈C:T-λI不为可逆算子},
σa(T)={λ∈C:T-λI不为下有界算子},
σb(T)={λ∈C:T-λI不为Browder算子},
σSF(T)={λ∈C:T-λI不为半Fredholm算子}。
令σ0(T)=σ(T)\σb(T), ρ(T)=C\σ(T), ρa(T)=C\σa(T), ρb(T)=C\σb(T)。
设A∈B(H), B∈B(K), 我们用MC=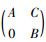
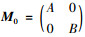
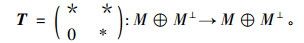
|
对上三角算子矩阵的研究方法之一是研究其主对角线上两个算子的性质, 近年来, 上三角算子矩阵备受关注[1-5]。本文主要研究了2×2上三角算子矩阵的平方满足(ω)性质的紧摄动的判定方法, 给出了2×2上三角算子矩阵的平方满足(ω)性质的紧摄动的充要条件。
2 算子矩阵的(ω)性质及其摄动1990年, H.Weyl[6]在检查Hermitian算子T的谱时发现, λ属于T的所有紧摄动的谱的充要条件是λ属于T的谱集但不是T的谱集中孤立的有限重特征值, 这个结论后来被人们称为Weyl定理, 20世纪90年代, 许多学者, 例如R.Harte和W.Y.Lee对Weyl定理进行了变形和推广, 定义了Browder定理[7], V.Rakocĉevic[8-9]给出了Weyl定理的另外两种变化:a-Weyl定理和(ω)性质。称T∈B(H)有(ω)性质[10], 若T满足σa(T)\σea(T)=π00(T), 其中算子T的本质逼近点谱σea(T)={λ∈C:T-λI∉SF+-(H)}, 这里
SF+-(H)={T∈B(H):T为上半Fredholm算子且ind(T)≤0},
集合π00(T)={λ∈isoσ(T):0 < n(T-λI) < ∞}。近年来有许多关于(ω)性质及其摄动的研究[10-11]。本文继续这样的工作, 主要研究上三角算子矩阵平方的(ω)性质及其摄动。若任给K∈K(H),T+K都具有(ω)性质, 称算子T具有(ω)性质的紧摄动。为了讨论上三角算子矩阵平方的(ω)性质的紧摄动, 先看几个引理。
引理1 T具有(ω)性质的紧摄动当且仅当下列条件成立:
1) ρea(T)=C\σea(T)连通;
2) isoσa(T)=σ0(T);
3) accσea(T)=accσa(T)。
证 明 由文献[12]的定理2.1可类似证明。
引理2[3] 设A∈B(H), B∈B(K), 则存在算子C∈B(K, H)使得2×2上三角算子矩阵MC∈SF+-(H⊕K)的充要条件是A∈B(H)是上半Fredholm算子, 且下列条件之一成立:
(a) 当R(B)闭时, n(B) < ∞且n(A)+n(B)≤d(A)+d(B)或者d(A)=n(B)=∞;
(b) 当R(B)不闭时, d(A)=∞。
下面给出本文的主要定理。
定理1 设A∈B(H), B∈B(K), 若M0具有(ω)性质且σa(M0)关于原点对称, 则对任意C∈B(K, H)(C≠0), MC2具有(ω)性质的紧摄动, σea(MC)关于原点对称且isoσea(MC)=Ø当且仅当下列条件成立:
1) F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=n(B-λI)=∞}=Ø;
2) E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø;
3) M0具有(ω)性质的紧摄动。
证 明 必要性 设对任意C∈B(K, H), C≠0, MC2具有(ω)性质的紧摄动, σea(MC)关于原点对称, 而且isoσea(MC)=Ø。首先证明对任意C∈B(K, H), C≠0, ρea(MC)连通。
反证法, 若ρea(MC)不连通, 则存在ρea(MC)的有界连通分支Ω, 且∂Ω⊆σSF(MC), 由文献[13]中引理2.10可知存在紧算子K1使得MC+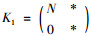
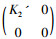
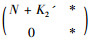
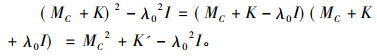
|
其中K'=MCK+KMC+K2是紧算子, 那么(MC+K)2-λ02I∈SF+-(H⊕K)。因为MC2具有(ω)性质的紧摄动, 故(MC+K)2-λ02I是下有界算子或Browder算子, 从而MC+K-λ0I下有界算子或Browder算子, 因此存在λ1∈Ω使得MC+K-λ1I是下有界算子, 于是N+K2'-λ1I是下有界算子。又因为N+K'2-λ1I是Weyl算子, 所以N+K2'-λ1I可逆, 这与σ(N+K2')=Ω矛盾。因此对任意C∈B(K, H), C≠0, ρea(MC)连通。
接着再证明对任意C∈B(K, H), C≠0, ρea(MC)=ρea(A)∩ρea(B)。
ρea(A)∩ρea(B)⊆ρea(MC)是显然的。反之, 设λ0∈ρea(MC), 则A-λ0I是上半Fredholm算子。我们断言A-λ0I是Weyl算子。事实上, 若A-λ0I不是Weyl算子, 则λ0∈intσ(A), 而ρea(MC)∩∂σ(A)⊆σ0(A)⊆isoσ(A), 显然isoσ(A)是孤立集, 我们知道一个孤立集至多是可数集[15], 所以一定存在一条封闭曲线L∈∂σ(A)使得λ0属于L围成的区域中且L∩ρea(MC)=Ø, 然而在L外一定存在一点λ1使得λ1∈ρea(MC), 这里λ1∈ρ(A)∩ρ(B), 但是λ0∈ρea(MC), 那么ρea(MC)不连通, 与已知矛盾。从而A-λ0I是Weyl算子, 再由引理2可知B-λ0I∈SF+-(K), 故λ0∈ρea(A)∩ρea(B), 对任意C∈B(K, H), C≠0, ρea(MC)=ρea(A)∩ρea(B)。
1) F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=n(B-λI)=∞}=Ø;
若不然, 设λ0∈F, 由引理2可知存在算子C∈B(K, H)使得MC-λ0I∈SF+-(H⊕K)。由ρea(MC)=ρea(A)∩ρea(B)得λ0∈ρea(A)∩ρea(B), 这与n(B-λ0I)=∞矛盾, 于是假设不成立。
2) E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø。
若不然, 设λ0∈E, 由引理2可知存在算子C∈B(K, H)使得MC-λ0I∈SF+-(H⊕K)。由ρea(MC)=ρea(A)∩ρea(B)得λ0∈ρea(A)∩ρea(B), 这与R(B-λ0I)=∞不是闭的矛盾, 于是假设不成立。
3) M0具有(ω)性质的紧摄动。
由引理1可知需要证明ρea(M0)连通; isoσa(M0)=σ0(M0)且accσea(M0)=accσa(M0)。
(ⅰ) ρea(M0)=ρea(A)∩ρea(B)。
ρea(A)∩ρea(B)⊆ρea(M0)是显然的。反之, 设λ0∈ρea(M0), 则A-λ0I, B-λ0I均是上半Fredholm算子, 且ind(A-λ0I)+ind(B-λ0I)≤0。对任意C∈B(K, H)(C≠0), MC-λ0I∈SF+-(H⊕K)。因为ρea(MC)=ρea(A)∩ρea(B), 所以λ0∈ρea(A)∩ρea(B)。因此可以得到ρea(M0)=ρea(A)∩ρea(B), 再由已知得到ρea(M0)连通。
(ⅱ) isoσa(M0)⊆σ0(M0)。
只需要证isoσa(M0)⊆σ0(M0)。设λ0∈isoσa(M0), 则存在δ > 0使得λ属于λ0的空心邻域B0(λ0; δ)时, M0-λI是下有界算子, 从而A-λI, B-λI均是下有界算子。于是对任意C∈B(K, H), C≠0, MC-λI是下有界算子。由此可知λ0∈isoσa(MC)∪ρa(MC), 下面分两种情况讨论。
情况1 当λ0∈isoσa(MC)时, 容易证明λ0∈isoσea(MC)∪ρea(MC), 由isoσea(MC)=Ø可知λ0∈ρea(MC)。而ρea(M0)=ρea(A)∩ρea(B)=ρea(MC), 那么就有λ0∈ρea(M0), 从而λ0∈σa(M0)\σea(M0)。再根据M0具有(ω)性质的事实, 可以得到λ0∈σ0(M0)。
情况2 当λ0∈ρa(MC)时, 因为ρea(M0)=ρea(A)∩ρea(B)=ρea(MC), 所以λ0∈ρea(M0), 易知λ0∈σa(M0)\σea(M0)。再由M0具有(ω)性质可知λ0∈σ0(M0)。
综合情况1和2可知isoσa(M0)=σ0(M0)。
(ⅲ) accσea(M0)=accσa(M0)。
只需要证明accσa(M0)⊆accσea(M0), 反证法, 若λ0∉accσea(M0), 易证对任意C∈B(K, H), C≠0, λ0∈isoσea(MC)∪ρea(MC), 由isoσea(MC)=Ø可知λ0∈ρea(MC)。由ρea(M0)=ρea(A)∩ρea(B)=ρea(MC)可知λ0∈ρea(M0), 于是λ0∈ρa(M0)∪[σa(M0)\σea(M0)], 因为M0具有(ω)性质, 所以λ0∈ρa(M0)∪σ0(M0)。易证λ0∈ρa(M0)∪isoσa(M0), 因此λ0∉accσa(M0), 从而accσea(M0)=accσa(M0)。
充分性 设条件1),2),3)成立。首先证明对任意C∈B(K, H), C≠0, isoσea(MC)=Ø。反证法, 若不然, 设λ0∈isoσea(MC), 则存在δ > 0使得λ属于λ0的空心邻域B0(λ0; δ)时, MC-λI∈SF+-(H⊕K), 从而A-λI是上半Fredholm算子。由F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=n(B-λI)=∞}=Ø和E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø, 再根据引理2可知B-λI是上半Fredholm算子, 且ind(A-λI)+ind(B-λI)≤0, 从而M0-λI∈SF+-(H⊕K), 于是λ0∈isoσea(M0)∪ρea(M0)。易证λ0∉ρea(M0), 那么λ0∈σea(M0)。因为M0具有(ω)性质的紧摄动, 由引理1可知λ0∈isoσa(M0)=σ0(M0), 于是A-λ0I和B-λ0I均是Browder算子, 从而对任意C∈B(K, H), C≠0, MC-λ0I是Browder算子, 这与λ0∈σea(MC)矛盾。
我们断言σ0(M0)关于原点对称。设λ0∈σ0(M0), 易知λ0∈isoσa(M0), 因为σa(M0)关于原点对称, 所以-λ0∈isoσa(M0), 根据引理1, 由M0具有(ω)性质的紧摄动, 可知-λ0∈σ0(M0)。
下证σea(M0)关于原点对称。设λ0∈ρea(M0), 因为M0具有(ω)性质, 所以λ0∈ρa(M0)∪σ0(M0)。又因为σa(M0)和σ0(M0)均关于原点对称, 从而-λ0∈ρa(M0)∪σ0(M0), 于是-λ0∈ρea(M0)。
再证对任意的C∈B(K, H), C≠0, σea(MC)关于原点对称。设λ0∈ρea(MC), 则A-λ0I是上半Fredholm算子, 根据引理2和F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=n(B-λI)=∞}=Ø以及E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø可知, B-λ0I是上半Fredholm算子且ind(A-λI)+ind(B-λI)≤0, 显然λ0∈ρea(M0)。于是λ0∈ρa(M0)∪[σa(M0)\σea(M0)]。由于M0具有(ω)性质, 那么就有λ0∈ρa(M0)∪σ0(M0)。利用条件σa(M0)和σ0(M0)均关于原点对称可知-λ0∈ρa(M0)∪σ0(M0), 那么可以得到M0+λ0I是下有界算子或Browder算子, 从而A+λ0I, B+λ0I同时是下有界算子或同时是Browder算子, 于是对任意C∈B(K, H), C≠0, -λ0∈ρea(MC)。
要证明MC2具有(ω)性质的紧摄动, 根据引理1可知需要证明:ρea(MC2)连通; isoσa(MC2)=σ0(MC2)且accσea(MC2)=accσa(MC2)。
首先容易证明当M0具有(ω)性质时, ρea(M0)=ρea(A)∩ρea(B)。下面分3步来证明:
1) 对任意C∈B(K, H), C≠0, ρea(MC2)=[ρea(A)∩ρea(B)]2。
设λ0∈ρea(A)∩ρea(B), 则λ0∈ρea(M0), 由此可知λ0∈ρa(M0)∪[σa(M0)\σea(M0)]。因为M0具有(ω)性质, 所以λ0∈ρa(M0)∪σ0(M0)。由σa(M0)和σ0(M0)均关于原点对称可知-λ0∈ρa(M0)∪σ0(M0), 则M0-λ0I, M0+λ0I同时是下有界算子或同时是Browder算子, 从而A-λ0I, A+λ0I, B-λ0I, B+λ0I同时是下有界算子或同时是Browder算子, 所以对任意C∈B(K, H), C≠0, λ02∈ρea(MC2)。反之, 设λ02∈ρea(MC2), 那么MC-λ0I, MC+λ0I均是上半Fredholm算子, 从而A-λ0I, A+λ0I均是上半Fredholm算子, 根据F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=n(B-λI)=∞}=Ø和E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø, 再由引理2可知B-λ0I, B+λ0I均是上半Fredholm算子, 而ind(M0-λ0I)+ind(M0+λ0I)=ind(A-λ0I)+ind(A+λ0I)+ind(B-λ0I)+ind(B+λ0I)≤0, 从而M0-λ0I和M0+λ0λ均是上半Fredholm算子, 且ind(M0-λ0I)和ind(M0+λ0I)中至少有一个小于等于零。再根据σea(M0)关于原点对称可知ind(M0-λ0I)≤0且ind(M0+λ0I)≤0, 于是±λ0∈ρea(M0)。由ρea(M0)=ρea(A)∩ρea(B)可以得到±λ0∈ρea(A)∩ρea(B), 那么λ02=[ρea(A)∩ρea(B)]2。于是对任意的C∈B(K, H), C≠0, ρea(MC2)=[ρea(A)∩ρea(B)]2。
下证ρea(MC2)连通。若不然, 则设存在隔离子集E, G⊆C使得ρea(MC2)=E∪G, 其中(E∪G)∪(E∪G)=Ø。设f(x)=x2, 于是[ρea(A)∩ρea(B)]2=f[ρea(A)∩ρea(B)], 而ρea(MC2)=[ρea(A)∩ρea(B)]2, 于是ρea(A)∩ρea(B)=f-1(E∪G), 其中f-1(E∪G)表示E∪G在映射f下的原像。而
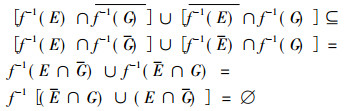
|
那么这就与ρea(A)∩ρea(B)的连通性矛盾。因此ρea(MC2)连通。
2) isoσa(MC2)=σa(MC2)。
只需要证明isoσa(MC2)⊆σa(MC2), 设μ0=λ02∈isoσa(MC2), 于是存在δ > 0使得μ属于μ0的空心邻域B0(μ0; δ)时, MC2-μI是下有界算子, 而ρea(MC2)=[ρea(A)∩ρea(B)]2=[ρea(M0)]2, 于是μ=λ2=[ρea(M0)]2。由σea(M0)关于原点对称可得±λ0∈ρea(M0), 于是λ0∈isoσea(M0)∪ρea(M0), 则λ0∉accσea(M0)。而M0具有(ω)性质的紧摄动, 由引理1可知λ0∉accσa(M0), 那么λ0∈isoσa(M0)∪ρa(M0)。事实上λ0∉ρa(M0), 若不然, 则由σa(M0)关于原点对称可知-λ0∈ρa(M0), 易证对任意C∈B(K, H), C≠0, λ02∈ρa(MC2), 这就与λ02∈σa(MC2)矛盾, 于是λ0∈isoσa(M0)。因为M0具有(ω)性质的紧摄动, 根据引理1可知λ0∈σa(M0), 再利用σ0(M0)关于原点对称可得-λ0∈σ0(M0), 因此A-λ0I, A+λ0I, B-λ0I, B+λ0I均是Browder算子, 于是对任意C∈B(K, H), C≠0, MC2-λ02I是Browder算子, 即μ0=λ02∈σ0(MC2)。
3) accσea(MC2)=accσa(MC2)。
只需证accσa(MC2)⊆accσea(MC2), 反证法, 设μ0=λ02∉accσea(MC2), 于是μ0=λ02∈isoσea(MC2)∪ρea(MC2), 下面分两种情况讨论:
情况1 若μ0=λ02∈isoσea(MC2)。则存在δ > 0使得μ属于μ0的空心邻域B0(μ0; δ)时, μ=λ2=ρea(MC2)。由ρea(MC2)=[ρea(A)∩ρea(B)]2=[ρea(M0)]2可知λ2∈[ρea(M0)]2。又因为σea(M0)关于原点对称, 从而±λ∈ρea(M0), 于是λ0∈isoσea(M0)∪ρea(M0)。由isoσea(MC2)=σ0(MC2)的证明过程可知μ0=λ02∈σ0(MC2), 于是μ0=λ02∉accσa(MC2)。
情况2 若μ0=λ02∈ρea(MC2)。因为MC2-λ02I=(MC-λ0I)(MC+λ0I), 所以MC-λ0I与MC+λ0I均为上半Fredholm算子。于是A-λ0I, A+λ0I均是上半Fredholm算子。根据F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)= n(B-λI)=∞}=Ø和E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø, 再依据引理2可以得到B-λ0I与B+λ0I均是上半Fredholm算子, 且ind(M0-λ0I)+ind(M0+λ0I)=ind(A-λ0I)+ind(A+λ0I)+ind(B-λ0I)+ind(B+λ0I)≤0, 那么M0-λ0I和M0+λ0I均是上半Fredholm算子, 而且ind(M0-λ0I)和ind(M0+λ0I)中至少有一个小于等于零。而σea(M0)关于原点对称的事实告诉我们ind(M0-λ0I)≤0且ind(M0+λ0I)≤0, 则±λ0∈ρea(M0)。因此±λ0∈ρa(M0)∪[σa(M0)\σea(M0)]。因为M0具有(ω)性质, 所以±λ0∈ρa(M0)∪σ0(M0), 从而M0-λ0I, M0+λ0I同时是下有界算子或同时是Browder算子, 也就是A-λ0I, A+λ0I, B-λ0I, B+λ0I同时是下有界算子或Browder算子, 故对任意C∈B(K, H), C≠0, μ0=λ02∈ρa(MC2)∪σ0(MC2), 于是μ0=λ02∈ρa(MC2)∪isoσa(MC2), 因此μ0=λ02∉accσa(MC2)。
从而由情况(1)和(2)可知accσea(MC2)=accσa(MC2)。
在定理1中, 在判断“M0满足(ω)性质的紧摄动”时, 需要判断算子A和B的相关谱集的性质, 下面根据算子A和B的相关谱集的特点来判断算子矩阵平方的(ω)性质的紧摄动。
推论1 设A∈B(H), B∈B(K)。若M0具有(ω)性质且σa(M0)关于原点对称, 则对任意C∈B(K, H)(C≠0), MC2具有(ω)性质的紧摄动, σea(MC)关于原点对称且isoσea(MC)=Ø当且仅当下列条件成立:
1) ρea(A)∩ρea(B)连通;
2) F={λ∈C:A-λI是上半Fredholm算子,d(A-λI)=n(B-λI)=∞}=Ø;
3) E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø;
4) isoσea(A)∩isoσea(B)=isoσea(A)∩ρea(B)=isoσea(B)∩ρea(A)=Ø。
证 明 必要性 由定理1的证明可知ρea(MC)=ρea(A)∩ρea(B)连通, 并且条件2),3)成立。因为M0具有(ω)性质的紧摄动(定理1), 所以isoσea(A)∩isoσea(B)⊆isoσea(M0)⊆isoσa(M0)=σ0(M0)⊆ρb(A)∩ρb(B), 然而[isoσea(A)∩isoσea(B)]∩[ρb(A)∩ρb(B)]=Ø, 于是isoσea(A)∩isoσea(B)=Ø。又因为isoσea(A)∩ρea(B)⊆isoσea(M0)⊆isoσa(M0)=σ0(M0)⊆ρb(A)∩ρb(B), 而[isoσea(A)∩ρea(B)]∩[ρb(A)∩ρb(B)]=Ø, 那么isoσea(A)∩ρea(B)=Ø, 同理可证isoσea(B)∩ρea(A)=Ø。
充分性 由定理1可知只需证M0具有(ω)性质的紧摄动, 由引理1可知需证ρea(M0)连通; isoσa(M0)=σ0(M0)且accσea(M0)=accσa(M0)。由M0具有(ω)性质容易证明ρea(M0)=ρea(A)∩ρea(B)连通。
对于isoσa(M0)=σ0(M0), 只需要证明isoσa(M0)⊆σ0(M0), 设λ0∈isoσa(M0), 那么λ0∈isoσa(A)∪ρa(A)且λ0∈isoσa(B)∪ρa(B)。下面分别讨论。
情况1 当λ0∈isoσa(A)∩ρa(B)时, 因为
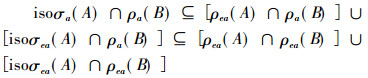
|
而已知isoσea(A)∩ρea(B)=Ø, 从而λ0=ρea(A)∩ρea(B)=ρea(M0), 于是λ0∈σa(M0)\σea(M0)。因为M0具有(ω)性质, 所以λ0∈σ0(M0)。
情况2 当λ0∈isoσa(B)∩ρa(A)时, 由情况1可类似证明。
情况3 当λ0∈isoσa(A)∩isoσa(B)时, 由于isoσa(A)∩isoσa(B)⊆[ρea(A)∩isoσa(B)]∪[isoσea(A)∩isoσa(B)]⊆[ρea(A)∩ρea(B)]∪[ρea(A)∩isoσea(B)]∪[isoσea(A)∩ρea(B)]∪[isoσea(A)∩isoσea(B)], 而根据已知
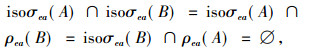
|
所以λ0∈ρea(A)∩ρea(B)=ρea(M0), 从而λ0∈σa(M0)\σea(M0), 再次利用M0具有(ω)性质的条件可知λ0∈σ0(M0)。
综合情况1,2和3可知isoσa(M0)=σ0(M0)。
对于accσea(M0)=accσa(M0), 只需要证明accσa(M0)⊆accσea(M0)。设λ0∉accσea(M0), 于是λ0∈isoσea(M0)∪ρea(M0), 断言λ0∉isoσea(M0), 事实上, 若λ0∈isoσea(M0), 由于
isoσea(M0)⊆[isoσea(A)∪ρea(A)]∩[isoσea(B)∪ρea(B)]⊆[isoσea(A)∪isoσea(B)]∪[isoσea(A)∪ρea(B)]∪[isoσea(B)∪ρea(A)]∪[ρea(B)∪ρea(A)], 而isoσea(A)∪isoσea(B)=isoσea(A)∪ρea(B)=isoσea(B)∪ρea(A)=Ø, 因此λ0∈ρea(A)∪ρea(B)=ρea(M0), 这与λ0∈σea(M0)矛盾, 从而λ0∈ρea(M0), 于是λ0∈ρa(M0)∪[σa(M0)\σea(M0)]。因为M0具有(ω)性质, 所以λ0∈ρa(M0)∪σ0(M0), 从而λ0∉accσea(M0)。
例1 设A, B∈B(l2)定义为:
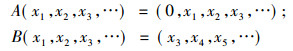
|
那么:
1) σa(M0)=σea(M0)={λ∈C:|λ|≤1}=σ(M0), 于是M0有(ω)性质且σa(M0)关于原点对称;
2) ρea(A)∩ρea(B)={λ∈C:|λ|>1}连通;
3) F={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=n(B-λI)=∞}=Ø;
4) E={λ∈C:A-λI是上半Fredholm算子, d(A-λI)=∞, n(B-λI) < ∞且R(B-λI)不是闭的}=Ø;
5) isoσea(A)∩isoσea(B)=isoσea(A)∩ρea(B)=isoσea(B)∩ρea(A)=Ø,
则对任意C∈B(l2, l2), MC2具有(ω)性质的紧摄动, σea(MC)关于原点对称且isoσea(MC)=Ø。
| [1] |
CAO X H, GUO M Z, MENG B. Semi-Fredholm spectrum and Weyl's theorem for operator matrices[J]. Acta Math Sinica, 2006, 22(1): 169-178. DOI:10.1007/s10114-004-0505-1 |
| [2] |
张敏, 曹小红, 吴学俪. 上三角算子矩阵的Wely型定理的摄动[J]. 陕西师范大学学报(自然科学版), 2015, 43(4): 10-15. |
| [3] |
CAO X H, MENG B. Essentail approximate point spectrum for operator matrices[J]. J Math Anal Appl, 2005, 304(2): 759-771. DOI:10.1016/j.jmaa.2004.09.053 |
| [4] |
DJORDJEVIC D S. Perturbation of spectra of operator matrices[J]. J Operator Theory, 2002, 48(3): 467-486. |
| [5] |
CAO X H. Browder spectra for upper triangular operator matrices[J]. J Math Anal Appl, 2008, 342(1): 477-484. DOI:10.1016/j.jmaa.2007.11.059 |
| [6] |
WEYL H. Vberbeschränkte quadratische Formen, deren Differenz vollstetig ist[J]. Rend Circ Mat Palermo, 1909, 27(1): 373-392. DOI:10.1007/BF03019655 |
| [7] |
HARTE R, LEE W Y. Another note on Weyl's theorem[J]. Trans Amer Math Soc, 1997, 349(5): 2115-2124. DOI:10.1090/S0002-9947-97-01881-3 |
| [8] |
RAKOĈEVIC V. Operators obeying a-Weyl's theorem[J]. Rev Roumaine Math Pures Appl, 1989, 34(10): 915-919. |
| [9] |
RAKOĈEVIC V. On a class of operators[J]. Mat Vesnik, 1985, 37(4): 423-426. |
| [10] |
AIENA P, PENA P. Variation on Weyl's theorem[J]. J Math Anal Appl, 2006, 324(1): 566-579. DOI:10.1016/j.jmaa.2005.11.027 |
| [11] |
AIENA P, BIONDI M T. Property (ω) and perturbations[J]. J Math Anal Appl, 2007, 336(1): 683-692. DOI:10.1016/j.jmaa.2007.02.084 |
| [12] |
SHI W J, CAO X H. Weyl's theorem for the square of operator and perturbations[J]. Commun Contemp, 2014, 17(5). |
| [13] |
JI Y Q. Quasitriangular+small compact=strongly irreducible[J]. Trans Amer Math Soc, 1999, 351(11): 4657-4673. DOI:10.1090/S0002-9947-99-02307-7 |
| [14] |
HERRERO D A. Economical compact perturbations, Ⅱ. Filling in the holes[J]. J Operator Theory, 1988, 19(1): 25-42. |
| [15] |
Jiang Z J, Wu Z Q, Ji Y Q. Real Function Theory[M]. 3nd ed.. Beijing: Higher Education Press, 2007: 28.
|
 2017, Vol. 47
2017, Vol. 47
 , 张敏
, 张敏