(拟)渐近非扩张映像和(拟)渐近伪压缩映像分别是(拟)非扩张映像和(拟)伪压缩映像的推广形式, 关于这些非线性映像的不动点之迭代算法的构造和强收敛性的讨论, 一些学者已进行了深入的研究[1-15]。2015年, 文献[4]在Hilbert空间的框架下, 设计出了几种修正的混杂投影算法, 并证明了这些算法生成的迭代序列能强收敛到有限族拟渐近伪压缩映像之公共不动点。另外, 文献[5]设计了无限族拟伪压缩映像之公共不动点的收缩投影算法, 并证明了该算法的强收敛性。受文献[4-5]的启示, 本文在Hilbert空间之框架下, 设计出一种新的关于无限族拟渐近伪压缩映像之公共不动点的复合迭代算法, 而且证明该迭代算法的强收敛性。本文的主要结果是文献[4-5]之相关结果的推广和改进。
1 预备知识设H代表实的Hilbert空间, 〈·, ·〉与‖·‖分别代表内积和范数符号, 设C是H之闭凸非空子集, N代表正整数集合。设T:C→C代表C到C的映像, 用F(T)代表T之不动点集合, 即F(T)={x∈C:Tx=x}。
定义1 称映像T:C→C是拟伪压缩映像, 如果F(T)≠Ø, 使得
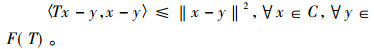
|
定义2 称映像T:C→C是渐近伪压缩映像, 如果存在一个序列{kn}⊂[1, ∞)满足kn→1, 使得
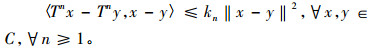
|
定义3 称映像T:C→C是拟渐近伪压缩映像, 如果F(T)≠Ø, 且存在一个序列{kn}⊂[1, ∞)满足kn→1, 使得
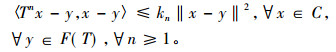
|
注1[4] 不动点集非空的渐近伪压缩映像是拟渐近伪压缩映像, 反之不真; 拟渐近伪压缩映像是拟伪压缩映像的推广。
定义4 称映像T:C→C是一致L-Lipschitz映像, 如果存在一个常数L > 0, 使得
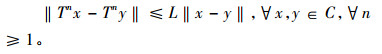
|
引理1[4] 设H表示实的Hilbert空间, C是H之闭凸非空有界子集, T:C→C是一致L-Lipschitz拟渐近伪压缩映像, 则F(T)是C之闭凸子集。
引理2[4] 设H是实的Hilbert空间, C是H之闭凸非空子集, PC:H→C代表H到C的度量投影, 则下列不等式成立:
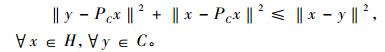
|
引理3[4] 设H是实的Hilbert空间, C是H之闭凸非空子集, 任给x∈H, z∈C, 则z=PCx的充要条件为
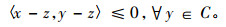
|
定理1 设H为实的Hilbert空间, C为H的闭凸有界子集, 设{Ti}i=1∞:C→C是一致Li-Lipschitz的拟渐近伪压缩映像族, 使得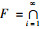
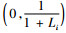
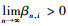
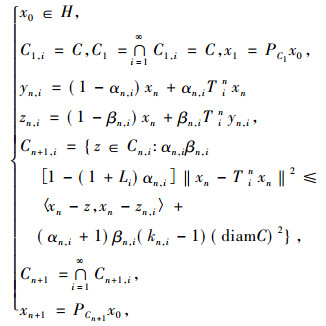
|
(1) |
这里kn, i是Ti的渐近常数, 则{xn}强收敛到PFx0。
证 明 分8步完成定理的证明。
第1步 证F为C的闭凸非空子集。
由引理1知F(Ti)为C的闭凸子集, ∀i∈N。再由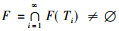
第2步 证Cn是闭凸集, ∀n≥1。
由Cn+1, i的构造直接可得Cn+1, i是闭凸集, 所以Cn+1是闭凸集, ∀n≥1。
第3步 证F⊂Cn, ∀n≥1。
只须证明F⊂Cn, i, ∀n≥1, ∀i∈N。
对n作数学归纳法进行证明, 显然F⊂C1, i=C。假设对某正整数n, F⊂Cn, i, 则对于每一p∈F⊂Cn, i, 由Ti是一致Li-Lipschitz的拟渐近伪压缩映像可得
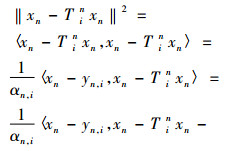
|
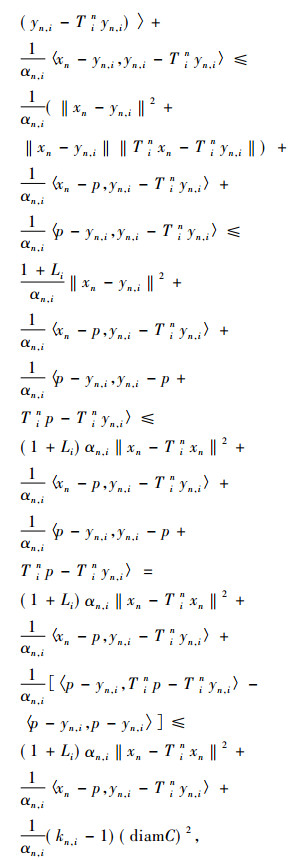
|
于是
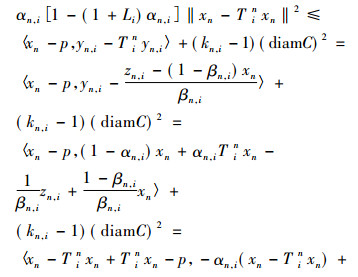
|
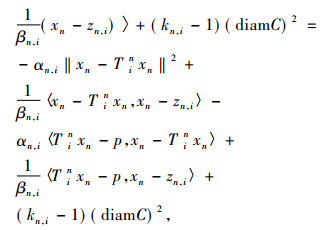
|
那么
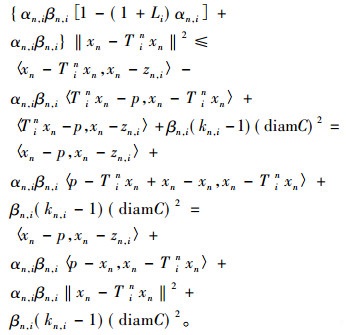
|
(2) |
其中
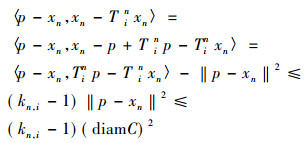
|
(3) |
式(3)代入(2)可得
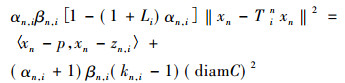
|
所以p∈Cn+1, i, 即F⊂Cn+1, i, 于是F⊂Cn, i, ∀n≥1, ∀i∈N。因此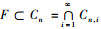
第4步 证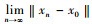
根据式(1)可得xn=PCnx0, 因为Cn+1⊂Cn且xn+1∈Cn+1, 所以
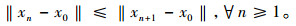
|
(4) |
另一方面, 从第3步知F⊂Cn, 所以
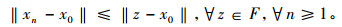
|
(5) |
结合式(4)和(5)可得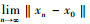
第5步 证xn→q(n→∞), q∈C。
设m > n≥1, 则xm=PCmx0∈Cm⊂Cn。根据引理2可得
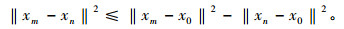
|
(6) |
令m, n→∞, 对式(6)两边取极限, 结合第4步可得
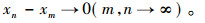
|
所以{xn}是柯西列, 于是xn→q(n→∞), q∈C。
第6步 证xn-Tin xn→0(n→∞)。
由第5步知xn+1-xn→0(n→∞)。由于xn+1∈Cn+1, i, 则
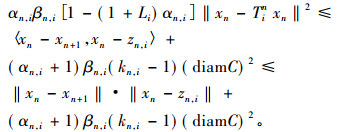
|
由{αn, i}, {βn, i}的假设和{xn}, {zn, i}的有界性以及kn, i→1(n→∞)可得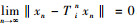
第7步 证xn-Tixn→0(n→∞), ∀i∈N。
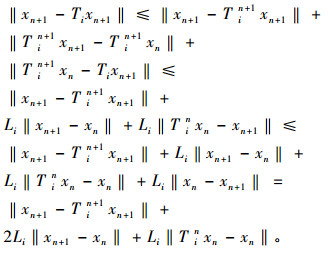
|
由第5步和第6步可得xn+1-Tixn+1→0(n→∞), ∀i∈N。
第8步 证q=PFx0。
因为xn→q且∀i∈N, xn-Tixn→0(n→∞), 又因为Ti是连续的, 所以q=Tiq, ∀i∈N, 于是q∈F。注意到F⊂Cn, xn=PCnx0, 由引理3可得
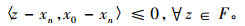
|
两边取极限得
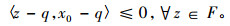
|
再由引理3可得q=PFx0。证毕。
注2 1)定理1将文献[4]中的主要结果从有限族拟渐近伪压缩映像推广到无限族拟渐近伪压缩映像上;
2) 定理1将文献[5]中的拟伪压缩映像族推广到拟渐近伪压缩映像族上。
3 数值实验为了说明算法(1)的有效性, 现给出具体的数值实验。
令T1=I, I表示实数集R上的恒等映像, T2:C→R为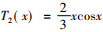
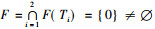
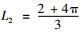
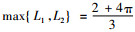
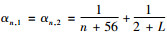
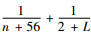
|
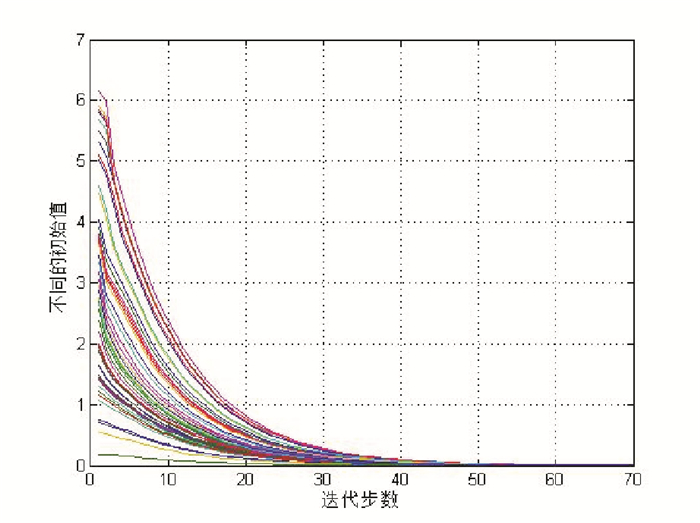
图 1 不同初始值下算法(1)的迭代曲线 Fig. 1 The iterative curves of algorithm(1) under different initial value |
注3 从图 1可看出, 本文中算法(1)对于不同初始值得到的序列均收敛。
4 结论近年来, 关于非线性映像的混杂投影迭代算法得到了广泛的研究, 本文的研究目的是进一步改进和发展拟渐近伪压缩映像族的公共不动点的混杂投影算法的迭代逼近问题。本文首先在Hilbert空间中构造出了一种新的无限族拟渐近伪压缩映像族的公共不动点的复合迭代算法, 其次利用拟渐近伪压缩映像的定义和度量投影的性质等证明了该算法的强收敛性, 最后给出具体的计算例子验证了所提出算法的有效性。本文的结果推广和补充了文献[4-5]及其他文献中的一些重要结论。能否去掉定理1中的集合C的有界性的限制条件, 是值得进一步研究的课题。
| [1] |
KIM T H, XU H K. Strong convergence of modified Mann iterations for asymptotically nonexpansive mappings and semigroups[J]. Nonlinear Analysis, 2016, 64: 1140-1152. |
| [2] |
ZHOU H Y. Demiclosedness principle with applications for asymptotically pseudo-contractions in Hilbert spaces[J]. Nonlinear Analysis, 2009, 70: 3140-3145. DOI:10.1016/j.na.2008.04.017 |
| [3] |
YAO Y H, POSTOLACHE M, KANG S M. Strong convergence of approximated iterations for asymptotically pseudocontractive[J]. Fixed Point Theory and Applications, 2014, 2014(100): 1-13. |
| [4] |
LIU Y X, ZHENG L G, WANG P Y, et al. Three kinds of new hybrid projection methods for a finite family of quasi-asymptotically pseudocontractive mappings in Hilbert spaces[J]. Fixed Point Theory and Applications, 2015, 2015(118): 1-13. |
| [5] |
高兴慧, 杨春萍. 关于Lipschitz拟伪压缩映像族的强收敛定理[J]. 浙江大学学报:理学版, 2016, 43(1): 71-74. |
| [6] |
GAO X H, ZHOU H Y. Shrinking projection methods for a family of quasi-ϕ-strict asymptotically pseudo-contractions in Banach space[J]. Journal of Mathematical Research and Exposition, 2011, 31(5): 905-914. |
| [7] |
高兴慧, 马乐荣. Lipschitz拟伪压缩映像族的收缩投影算法[J]. 数学的实践与认识, 2014, 44(20): 254-257. |
| [8] |
高兴慧, 周海云, 高改良. 平衡问题和不动点问题的公共元的混杂算法[J]. 数学物理学报, 2011, 31A(3): 720-728. |
| [9] |
GAO X H, ZHOU H Y. Strong convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces[J]. Acta Mathematics Applicatae Sinica, English Series, 2012, 28(2): 337-350. DOI:10.1007/s10255-012-0148-4 |
| [10] |
ZHOU H Y, WANG P Y. A new iteration method for variational inequalities on the set of common fixed points for a finite family of quasi-pseudocontractions in Hilbert spaces[J]. Journal of Inequalities and Applications, 2014, 2014(218): 1-12. |
| [11] |
HE H M, LIU S Y, ZHOU H Y. An explicit method for finding common solutions of variational inequalities and systems of equilibrium problems and fixed points of an infinite family of nonexpansive mappings[J]. Nonlinear Analysis, 2010, 72: 3124-3135. DOI:10.1016/j.na.2009.12.002 |
| [12] |
WEI L, BA Y C, AGARWAL R P. New ergodic convergence theorems for non-expansive mappings and m-accretive mappings[J]. Journal of Inequalities and Applications, 2016, 2016(22): 1-20. |
| [13] |
DONG Q L, HE S N, CHO Y J. A new hybrid algorithm and its numerical realization for two nonexpansive mappings[J]. Fixed Point Theory and Applications, 2015, 2015(150): 1-12. |
| [14] |
高兴慧, 周海云. Hilbert空间中拟非扩张映像族的逼近定理[J]. 武汉大学学报:理学版, 2011, 57(2): 123-126. |
| [15] |
张弘, 薛西锋. 锥Banach空间中多个自映射的公共不动点定理[J]. 西北大学学报:自然科学版, 2016, 46(2): 157-161. |
 2017, Vol. 47
2017, Vol. 47