2. 石家庄经济学院 数理学院,河北 石家庄 050031
2. School of Mathematics and Sciences, Shijiazhuang University of Economics, Shijiazhuang 050031, China
史福贵教授[1]定义了(L, M)-fuzzy拟阵(它是分明拟阵[2-3]和GV模糊拟阵[4-11]的一般化)并且推广了分明拟阵的一些结果。然而由于一般完全分配格[12]的结构很复杂, 将分明拟阵中的有些内容(比如拟阵的运算及性质)推广到(L, M)-fuzzy拟阵中是极其困难的事。特殊化是一种可以尝试的解决这些问题的策略。(L, M)-fuzzy拟阵包括两个特殊类: L-拟阵类和M-模糊化拟阵类, 对于后者研究成果已经很丰富(参见文献[13-14]), 对于前者即使研究特殊情形[15](比如GV模糊拟阵)也困难重重。为了基于特殊化思想探寻解决问题的办法(同时也从实际应用考虑), 本文将研究比GV模糊拟阵还特殊的一类L-拟阵(即GV状模糊拟阵)的性质, 其中L={0, 0.5, 1}⊆[0, 1]。
1 GV状模糊拟阵及其等价刻画设S为有限集, |S|是它的基数或势, L是完全分配格(本文将2和{0, 1}不加区分), LS是从S到L的映射(又叫S上的L-子集)的全体。则LS依点式序(仍用≤表示)构成一个完全分配格。用hT表示S上的在T上恒等于h,在S-T上恒等于0的L-子集(T⊆S, h∈L); 称L-子集h{x}(也记作Sxh, h∈L-{0})为尖。对每个ξ∈LS, 记↓ξ={η∈LS|η≤ξ}, 用m(ξ)表示R+(ξ)={ξ(x)|x∈S}-{0}的下确界, 称suppξ={x∈S|ξ(x)>0}为ξ的承载集,ξ[r]={x∈S|ξ(x)≥r}为ξ的r-水平截集(r∈L-{0}),ξ|T=ξ∧1T为ξ在T上的限制(T⊆S)、∑x∈Sξ(x)为ξ的基数或势(记作|ξ|); 当η≤ξ且η≠ξ时记η < ξ。对每个






定义1[1] 设S是有限集。则称满足下列条件的

(LI1) 0S∈
(LI2) 若λ∈

(LI3) 若λ, μ∈

若
(LI4) {μ∈LS|bμ[b]∈


下文中我们约定L={0, 0.5, 1}⊆[0, 1]。此时的L-拟阵仍然可能是不完全的。考虑2元素集合S={x, y}并且令


首先给出完全L-拟阵的等价刻画。
定理1 设S是有限集,
1) 若(S, 

2) (S, 

① 由于这种完全L-拟阵很像GV模糊拟阵,因此本文中也称其为GV状模糊拟阵。
(*)对

3) 若(S, 


证 明 1)设(S, 







取S={x, y, z}为3元素集,J=↓0.5S∪↓1{y, z}∪{0.5{x}∨1{y, z}}。则



2) 必要性。易见(



ⅰ) 若b=0.5, 取λ=ξ∨μ,则λ[0.5]=supp μ∪{y}且λ[1]=μ[1], 因此0.5λ[0.5]=ξ∈


ⅱ) 若b=1,则当min{m(μ), m(ν)}=1时由(LI3)易见(*)成立。当min{m(μ), m(ν)}=0.5时令η=0.5ν[0.5], ζ=0.5μ[0.5].则0.5=‖η‖(|supp ν|)>‖ζ‖(|supp ν|)=0, 从而由(LI3)知存在y∈supp ν-supp μ使得ξ=0.5supp ζ∪y∈



充分性。设ν, μ∈










3) 只证μ∈LS满足μ[a]∈






称S上的满足Γ(0.5)⊇Γ(1)的拟阵独立集系族Γ={Γ(0.5), Γ(1)}为S上的一个拟阵塔。S上的拟阵塔的全体记作T(S, L)。下面的定理2说明可以用拟阵塔确定GV状模糊拟阵。
定理2 1)对每个






2) 存在T(S, L)上的偏序关系≤使得(1)中的φS:(I(S, L), ⊆)→(T(S, L), ≤)和ψS:(T(S, L), ≤)→(I(S, L), ⊆)都是保序映射(此时称φS和ψS是序同构)。
证 明 1) 由定理1可知φS和ψS都是映射。因Γ















2) 对于T(S, L)的任意两个元素Γ1={Γ1(0.5), Γ1(1)}和Γ2={Γ2(0.5), Γ2(1)}, 规定Γ1≤Γ2⇔Γ1(a)⊆Γ2(a)(∀a∈L-{0}), 则易见由此定义的≤是T(S, L)上的偏序关系。下面证明φS和ψS都保序。首先证φS:(I(S, L), ⊆) →(T(S, L), ≤)是保序的。设







本节证明可以用GV状模糊拟阵基系确定GV状模糊拟阵(见下面的定理3)。
定义2 设S是有限集。称
1) 
2) Low(
3) 

定义3 设S是有限集。若




定理3 1) 对每个









2) 存在B(S, L)上的偏序关系≤使1)中的φS:(I(S, L), ⊆)→(B(S, L), ≤)和ψS:(B(S, L), ≤)→(I(S, L), ⊆)都是保序映射。
证 明 1) Step 1 对于每个






















Step 2 对于每个



Case 1 min{m(μ), m(ν)}=0.5。因I=Low({supp μ|μ∈
Case 2 min{m(μ), m(ν)}=1。由supp μ=μ[1]和supp ν=ν[1]知|μ[1]| < |ν[1]|。因I=Low(
Step 3 容易验证







2) 对于B(S, L)的任意两个元素




本节定义GV状模糊拟阵秩函数并证明可以用它生成GV状模糊拟阵(见下面的定理4)。
定义4 设S是有限集。则称满足以下条件的映射R:LS→[0, ∞)为S上的一个GV状模糊拟阵秩函数(S上的GV状模糊拟阵秩函数的全体记作R(S, L)):
(LR1) 0≤R(μ)≤|μ|(∀μ∈LS)。
(LR2) 若μ, ν∈LS且μ≤ν, 则R(μ)≤R(ν)。
(LR3) R(μ)+R(ν)≥R(μ∨ν)+R(μ∧ν)(∀μ, ν∈LS)。
(LR4) R(Sxh)∈{0, sup{h∧μ(x)|μ∈
(LR5) 若μ∈LS满足m(μ)≥h且x∈S-supp μ, 则R(μ∨Sxh)-R(μ)∈{0, h}。
定理4 对每个R∈R(S, L), 
证 明 Step 1 |μ|+|ν|=|μ∨ν|+|μ∧ν|(∀μ, ν∈LS)。令X={x∈S|μ(x)≥ν(x)}, Y={x∈S|μ(x) < ν(x)}。则X∪Y=S且X+Y=Ø, 从而有
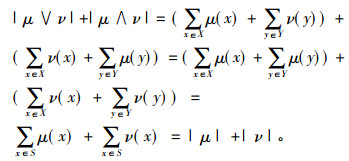
|
Step 2 设μ∈LS, h∈{0}, X⊆S。用归纳法和Step 1的结论可以证明R



Step 3 对每个R∈R(S, L), 


首先证明(


Case 1 A=supp μ, B=supp ν且ν=μ|B。假设ν∉
Case 2 

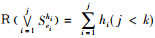
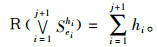
|
(1) |
令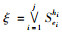
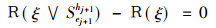
|
(2) |
下面只须证明式(2)不可能成立。若不然, 令C={e1, e2, …, ej}且μC=μ|C, 则由(LR5)可得

|
(3) |
或者

|
(4) |
令D=C∪{ej+1}, μD=μ|D, γ=μC∨Sej+1hj+1, β=μ|{ej+1}。若式(3)成立, 则由(LR3)和(LR4)得|μD|=|μC∨β| =|μC|+|β|=R(μC)+R(β)=R(μC∨Sej+1hj+1)+R(β)=R(γ)+R(β)≥ R(γ∨β)+R(γ∧β) = R(μD)+R(Sej+1hj+1)=|μD|+hj+1, 矛盾(因hj+1>0)。若式(4)成立, 则由式(2)和(LR3)-(LR4)得|μC|+|ξ|=R(μC)+R(ξ∨Sej+1hj+1)≥R(μC∨ξ∨Sej+1hj+1)+R(μC∧(ξ∨Sej+1hj+1))=R(μC∨Sej+1hj+1)+ R(ξ)=|μC|+hj+1+|ξ|, 矛盾(因hj+1>0)。
接下来证明




本文证明了可以用拟阵塔或GV状模糊拟阵基系确定GV状模糊拟阵独立集系, 可以由GV状模糊拟阵秩函数导出GV状模糊拟阵独立集系。由于文中使用的方法颇具一般性, 因此通过完善秩函数的定义证明|B(S, L)|=|I(S, L)|并且将所得结果推广到更一般的L-拟阵情形将是有待进一步完成的工作。
| [1] |
SHI F G. (L, M)-fuzzy matroids[J]. Fuzzy Sets and Systems, 2009, 160: 2387-2400. DOI:10.1016/j.fss.2009.02.025 |
| [2] |
OXLEY J G. Mlatroid Theory[M]. Oxford: Oxford University Press, 1992: 234-260.
|
| [3] |
赖虹建. 拟阵论[M]. 北京: 高等教育出版社, 2002.
|
| [4] |
GOETSCHEL R, VOXMAN W. Fuzzy matroids[J]. Fuzzy Sets and Systems, 1988, 27(3): 291-302. DOI:10.1016/0165-0114(88)90055-3 |
| [5] |
GOETSCHEL R, VOXMAN W. Bases of fuzzy matroids[J]. Fuzzy Sets and Systems, 1989, 32(2): 253-261. |
| [6] |
GOETSCHEL R, VOXMAN W. Fuzzy circuits[J]. Fuzzy Sets and Systems, 1989, 32(1): 35-43. DOI:10.1016/0165-0114(89)90086-9 |
| [7] |
GOETSCHEL R, VOXMAN W. Fuzzy matroids and a greedy algorithm[J]. Fuzzy Sets and Systems, 1990, 37(2): 201-213. DOI:10.1016/0165-0114(90)90043-6 |
| [8] |
GOETSCHEL R, VOXMAN W. Fuzzy matroid structures[J]. Fuzzy Sets and Systems, 1991, 41(3): 343-357. DOI:10.1016/0165-0114(91)90137-F |
| [9] |
GOETSCHEL R, VOXMAN W. Fuzzy rank functions[J]. Fuzzy Sets and Systems, 1991, 42(2): 245-248. DOI:10.1016/0165-0114(91)90150-O |
| [10] |
GOETSCHEL R, VOXMAN W. Spaming properties for fuzzy matroids[J]. Fuzzy Sets and Systems, 1992, 51(3): 313-321. DOI:10.1016/0165-0114(92)90022-V |
| [11] |
NOVAK L. On Goetschel and Voxman fuzzy matroids[J]. Fuzzy Sets and Systems, 2001, 117(3): 407-412. DOI:10.1016/S0165-0114(98)00424-2 |
| [12] |
GIERZ G, HOFMANN K H, KEIMEL K, et al. 2nd ed. Continuous Lattices and Domains[C]// vol. 93 of Encyclopedia of Mathematics and Its Applications.Cambridge: Cambridge University Press, 2003.
|
| [13] |
史福贵. 格值模糊拟阵的研究进展[J]. 模糊系统与数学, 2012, 26(6): 1-13. DOI:10.3969/j.issn.1001-7402.2012.06.001 |
| [14] |
史福贵, 修振宇. 模糊化拟阵的最新进展[J]. 聊城大学学报(自然科学版), 2015, 28(2): 1-11. DOI:10.3969/j.issn.1672-6634.2015.02.001 |
| [15] |
XIN X, SHI F G. Rank functions for closed and perfect[0, 1]-matroids[J]. Hacet J Math Stat, 2010, 39(1): 31-39. |
 2017, Vol. 47
2017, Vol. 47