2. 中国科学院大学 人文学院,北京 100049
2. School of Humanities, University of Chinese Academy of Sciences, Beijing 100049, China
作为19世纪最伟大的数学创造之一, 100多年以来, 代数几何学已经成为数学的核心组成部分。代数几何几乎与全部数学分支都存在紧密的联系, 而且相互促进、共同发展。代数几何学主要研究由多项式方程或方程组定义的代数曲线、代数曲面和代数簇(代数曲线的n维推广)。可以把代数曲线看作代数函数的根所构成的集合, 即由一个多项式方程P(x, y)=0所定义的y=f(x)。由此, 可以看出代数与几何之间的对应关系, 有些几何问题和代数问题就可以借此相互渗透、影响和转化。环包括交换环和非交换环, 起源于19世纪早期。交换环的主要来源是代数数论、代数几何和不变量理论这三大分支[1-3]。目前国内对交换环论在代数数论中的历史起源已有一些成果[4-7]。本文主要探讨交换环论与代数几何的一些关联和作用。
1 代数曲线的研究方法综观数学的历史发展, 代数曲线的研究方法多种多样、各有特色。比如解析方法、几何代数方法以及代数算术方法、超越方法和拓扑方法等, 从而形成了各有优长的数学理论体系。
在十九世纪50年代, 黎曼(G. F. B. Riemann, 1826—1866)在研究代数几何问题时, 首先运用了解析方法。解析方法的重点是, 研究复变量的代数函数f(w, z)=0及其积分。黎曼通过引入黎曼面的概念, 使黎曼面上的代数函数变为单值函数。用现代的术语来说, 黎曼面就是连通的一维复流形。黎曼是经典代数几何学的奠基者之一, 他引入了拓扑学的观点, 证明黎曼-罗赫定理的特殊情形。黎曼-罗赫定理是代数几何学的基本定理和重要工具, 可以计算具有指定零点和极点的亚纯函数空间的维数。黎曼还引入双有理变换及其不变量和参模等概念。黎曼的方法严格性欠缺。
十九世纪六七十年代, 克莱布什(R.R.F.Clebsch, 1833—1872)、戈丹(P.Gordan, 1837—1912)、布瑞尔(A. W. V. Brill, 1842—1935)、马克斯·诺特(M. Noether, 1844—1921)等数学家开始运用几何代数方法来研究代数函数和代数曲线。布瑞尔与马克斯·诺特创立了线性工具。马克斯·诺特所研究的问题是:已知两条代数曲线f(x, y)=0和g(x, y)=0, F(x, y)在什么条件下可以表示为F=Af+Bg的形式(其中A, B是x, y的多项式)?如果换作现在的术语, 那么问题就是:在什么条件下, F是由f和g生成的多项式环R[x, y]理想中的一个元素。这是多项式理想理论的起点。马克斯·诺特又是抽象环论的建立者爱米·诺特(E. Noether, 1882—1935)的父亲, 马克斯·诺特对爱米·诺特在环论方面的工作是有直接和间接影响的[8]。
解析方法和几何代数方法虽然新颖有效, 但均未给代数函数论建立起严格的基础。数学以精密科学而著称, 代数函数论的严格化势在必行。
戴德金(R. Dedekind, 1831—1916)和韦伯(H. Weber, 1842—1913)在1882年发表文章“单变量的代数函数理论”(Theorie der algebraischen Funktionen einer Veränderlichen)[9]。准备以一种最简单、严格和一般的形式, 为代数函数论建立起一个基础。戴德金之前研究代数数域, 自然想到把研究代数数域的方法移植到代数函数域中。
代数数域为有理数域Q的有限扩域Q(α), 代数函数域为有理函数域C(z)的有限扩域K=C(z)(w)。戴德金看到了这种相似性, 进而考虑相关的一些问题。具体来说, w为多项式a0+a1α+a2α2+…+anαn的根, 其中ai∈C(z)。由此可以得到:w=f(z)为一个由多项式方程P(z, w)=a0+a1w+a2w2+…+anwn=0所确定的代数函数。实际上, K=C(z)(w)=C(z, w)的全部元素均为代数函数[3]。
假设A是C(z)上的有限扩域K的整环, 即A由K中是C(z)上首一多项式的根的全部元素组成。对于代数函数来说, A的每一个非零理想均可唯一表示为素理想的乘积。黎曼面上的亚纯函数形成一个代数函数域, 而整函数为这个域的整环。
戴德金和韦伯相当于为代数函数域K上的黎曼曲面S给出一个严格的代数定义做好了准备工作, 用现代的术语来说, 它就是K上非平凡离散值的集合。S的有限点对应A的理想, 对于S的无限远点, 则引入了其他新的数学概念。因此, 戴德金和韦伯成功实现了最初的想法, 把黎曼的关于代数函数的大部分思想严格地以代数形式表示出来。特别地, 他们对黎曼-罗赫定理亦给出一个严格的证明。
总之, 戴德金和韦伯给大部分黎曼代数函数理论建立起了坚实的基础, 并取得了概念性突破, 明确了代数数域和代数函数域的一些相似性, 也明确了代数几何与代数数论之间的一些相似性, 并为它们提供了共同的代数学基础。几何的背景开始消弱, 推进了抽象代数学的产生, 尤其是理想、模、域和环的理论。因为抽象代数的语言不依赖基域C的拓扑, 所以戴德金和韦伯的结果更具一般性。这种相似性为代数函数域和代数数域的发展创造了很好的契机, 带来了丰富成果。举例来讲, 在代数几何上使用幂级数, 使得亨泽尔(K. Hensel, 1861—1941)提出了p进数。亨泽尔对第一个提出抽象环定义的弗兰克尔(A. Fraenkel, 1891—1965)产生影响。戴德金和韦伯还推广了这种思想, 使之适用于任意的域。这样, 代数几何的思想就转化到数论中, 一跃成为一种研究数论的新的强有力方法与工具[8]。
因此, 如果要探讨环论在代数几何中的起源, 也就是探讨多项式理想理论, 就要从马克斯·诺特的相关工作谈起。之后, 希尔伯特(D. Hilbert, 1862—1943)、拉斯克尔(E. Lasker, 1868—1941)和麦考莱(F. S. Macaulay, 1862—1937)分别在多项式理想论方面做出了一些重要贡献。
2 希尔伯特对多项式理想论的贡献代数几何的研究对象是代数曲线和代数簇, 而要研究代数簇就需研究多项式理想, 因此多项式的理想这一问题十分关键。一个代数簇V是Rn(或Cn)中满足多项式方程组fi(x1, x2, …, xn)=0(i=1, 2, …)的点集。也就是, 一个代数簇为多项式集合的全部公共零点解的集合。这就要提到希尔伯特基定理。
希尔伯特在代数数论、代数几何、不变量理论、几何基础、变分法、积分方程、物理学等多个分支都有贡献。在19世纪末和20世纪初, 他给出了很多重要的结果和启示。他研究了有限个变量的表达式, 即研究这些变量的多项式环, 证明了基定理, 即系数在给定域中的有限个变量的多项式环, 它的每一个理想均有一组有限基。
我们知道, 代数学基本定理建立起了代数与几何的关系, 表明复数域上的单变量的多项式是由其根的集合来确定的, 而根的集合属于内在的几何对象。希尔伯特基定理指出存在有限多个方程满足这个条件, 不同的多项式方程组有可能会得到相同的根的集合。
举例来讲, R3中平行于xoy平面且在其上两个单位的平面内的半径为2的圆可表示为下面一些形式:
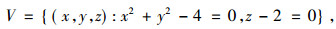
|
或
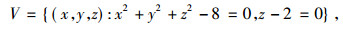
|
或
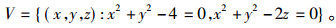
|
如果多项式f1, f2, …, fm在V的点处为零, 那么集合I={g1f1+g2f2+…+gmfm:gi∈R[x, y, z]}在V的点处也为零。I是多项式环R[x, y, z]的理想。R[x, y, z]中全部在V上为零的多项式集合也是一个理想, 就是表示V的多项式集合。
上面已经给出了环R[x1, x2, …, xn](或C[x1, x2, …, xn])的理想与Rn(或Cn)上的簇的对应:如果V是一个簇, 令I(V)={f(x1, x2, …, xn)∈R[x1, x2, …, xn]:对于所有的(a1, a2, …, an)∈V都有f(a1, a2, …, an)=0};如果J是环R[x1, x2, …, xn]的一个理想, 令V(J)={(b1, b2, …, bn)∈Rn:对于所有的g∈J都有g(b1, b2, …, bn)=0}[3]。
希尔伯特零点定理是:如果簇V(J)在Cn中或在任意的代数闭域K的Kn中, 那么V(J)≠∅。希尔伯特零点定理确定了多项式环的理想和仿射空间子集之间的基本对应。因此, 运用零点定理及其相关结果, 我们就可以运用代数的概念来阐释簇的几何概念, 亦可用几何概念来解读环论中的若干问题。这种联系在代数几何中至关重要, 是代数闭域K上的簇和它所确定的最大理想(即所谓的根理想)之间的一一对应。在这种情况下, 素理想对应着不可约簇。
3 拉斯克尔和麦考莱对多项式理想论的贡献拉斯克尔是德国数学家和世界象棋冠军, 他推广和创新了前人的成果, 给出了理想的准素分解, 具有标志性意义。拉斯克尔实际上给出了理想的准素分解:多项式环F[x1, x2, …, xn]的每一个理想为准素理想的有限交。
在现代的抽象环中, 任意一个环R的一个理想A称为准素理想, 若给定R里的两个元素a和b, 使得它们的积ab属于A但a不属于A, 则存在一个整数k满足kbk属于A。任意的素理想均为准素理想。在整数环Z中, 准素理想与素数的幂相对应。
拉斯克尔把准素理想当成素理想的推广, 首先给出了准素理想的定义, 认为准素理想和素理想的关系相当于整环中素数幂和素数的关系。若运用代数几何的语言来描述这个代数数论中的结果, 则是每一个代数簇均为不可约代数簇的有限并, 即簇不可以被非平凡地分解为其他簇的有限并。
因此, 准素理想的概念起源于多项式理想。拉斯克尔受到了库默尔(E. E. Kummer, 1810—1893)、戴德金、克罗内克(L. Kronecker, 1823—1891)等数学家对理想论的贡献、希尔伯特对不变式的贡献以及马克斯·诺特等数学家对代数几何的贡献的综合影响, 并把这些数学家的先进成果吸收和再创造。
事实上, 1888至1891年间, 拉斯克尔在柏林、海德堡和哥廷根学习。此后, 在爱尔兰学习并获得博士学位, 师从马克斯·诺特。1905年, 他在《数学年刊》上发表“模和理想论”(Zur Theorie der Moduln und Ideale)[10], 介绍了模和理想等概念, 得到了关于多项式和不变量的一些结果, 首次明确定义了多项式的准素理想, 其中希尔伯特给出的零点定理起到重要作用。
拉斯克尔研究了一个重要原则, 并称之为史纳曼原则(Prinzip Von Schönemamm)。史纳曼(T. Schönemann, 1812—1868)是勃兰登堡的一个高等学校教师。史纳曼研究同余理论, 亦为德国最早研究伽罗瓦理论的数学家。
拉斯克尔与希尔伯特一样, 推崇戴德金的概念和思想, 沿用了许多戴德金的思想和符号, 运用因子分解的一些性质, 证明了因子分解定理。
除此之外, 拉斯克尔还发展了模代数。若一个带有n个变量的多项式集合M符合下面两个条件:
1) 若F是M中的一个元素, α为任意一个关于n个变量的多项式, 则αF属于M;
2) 若F1和F2属于M, 则它们的和F1+F2也属于M,
则集合M是一个多项式模。
模M的一个基是一个有限的子集合F1, …, Fk, M中的任意一个元素可以表示为x1F1+…+xkFk的形式, 其中xi(i=1, …, k)表示任意多项式。
我们知道, 希尔伯特证明了每个多项式存在一个有限基, 还证明了零点定理, 由此可得, 给定一个多项式的有限集合F1, …, Fh和另外一个多项式F, 若F对于F1, …, Fh的全部公共根为零, 则存在一个自然数k和h个多项式A1, …, Ah, 使得Fk=A1F1+…+AhFh。
拉斯克尔将准素理想作为模论的核心概念。若一个模中的全部多项式在点a1,a2,…,an处为零, 则称它包含点a1, a2…, an。拉斯克尔给出了一个主要定理:每个模能够表示成有限个准素模和不包含点的模的交集。他还给出了另一个定理:对属于与一个准素理想M相伴的素理想P的每个型f来说, 存在一个整数h, 它满足fh是M的一个元素。要证明这个定理, 用到了一个引理:给定一个无限的理想序列M1, M2, …, 存在一个自然数n, 使得当N>n时, 模MN包含在(M1, M2, …, MN)里, 即包含在模M1, M2, …, MN的最小公倍数里。这个引理可以用希尔伯特基定理来证明, 与升链条件等价[11]。而升链条件是爱米·诺特所格外重视和应用的, 并提炼出了诺特环。
后来, 麦考莱补充了拉斯克尔的结果, 因此, 多项式理想分解成准素理想的定理, 通常又称作拉斯克尔-麦考莱定理。
麦考莱毕生在中学教书, 共写有14篇关于代数几何和多项式理想论的文章, 主要研究代数曲线、黎曼-罗赫定理以及代数多项式。1913年, 麦考莱在文章“关于一个给定的模系统分解为包含希尔伯特数性质的准素分支”(On the Resolution of a given Modular System into Primary Systems including some Properties of Hilbert Numbers)[12]中证明了因子分解的唯一性, 并给出了一种具体算法。他是通过在一个准素分解里孤立的准素模和嵌入的准素模之间的麦考莱微分法来完成这项工作的。因子分解当中的一个准素模称为孤立的, 若其代数结构未包含在其余准素分支的代数结构的并集中, 反之, 则称为嵌入的。麦考莱证明了:在一个因子分解里, 孤立的准素模唯一, 嵌入的准素模不唯一。相比较而言, 拉斯克尔的因子分解包括一个不包含点的模。这个模在麦考莱的因子分解里不存在, 这是因为麦考莱只研究齐次系, 在其中全部的多项式至少包含原点。麦考莱给出了一种变换, 每个多项式系都可以运用它变换到一个齐次多项式系中, 因此, 他可以用到全部拉斯克尔得出的结果。麦考莱证明了准素分解的唯一性, 即预示着每一个簇可以被表示为唯一的不可约簇的有限并, 这是一类关于簇的重要算法定理[13-14]。
4 结语多项式理想理论是交换环论的重要组成部分。代数几何研究代数曲线以及代数簇, 多项式理想理论是探讨交换环论的缘起时必要且关键的一环。马克斯·诺特、希尔伯特、拉斯克尔、麦考莱等人一脉相承, 善于吸收和创新, 前仆后继所建立起来的多项式理想论, 奠定了高维交换代数的基础。不过, 当时的交换环论还是具体的:一方面是复数域上的多项式环及其理想理论, 另一方面还未从域的概念中摆脱出来成为环的理论。摆脱具体环的限制真正迈入抽象交换环理论的数学家是爱米·诺特。她把具体的多项式理想理论等纳入到一个抽象体系, 完成了对于抽象环的公理刻画, 证明了理想的升链条件与有限基条件和极大条件等价, 证明了一般形式的准素分解定理, 从而建立起了一般的抽象环论。
| [1] |
胡作玄. 近代数学史[M]. 济南: 山东教育出版社, 2006: 536-537.
|
| [2] |
张英伯, 王凯顺.代数学基础(上下册)[M].北京: 北京师范大学出版社, 2012, 13: 1-10.
|
| [3] |
KLEINER I. A History of Abstract Algebra[M]. New York: Springer, 2007: 41-50.
|
| [4] |
王淑红, 邓明立. 抽象环概念的历史演变[J]. 科学技术哲学研究, 2011, 28(4): 84-87. |
| [5] |
王淑红, 邓明立. 弗兰克尔:一代公理化集合论大师[J]. 自然辩证法通讯, 2015, 37(1): 134-141. |
| [6] |
王淑红, 邓明立. 戴德金对理想论的贡献[J]. 自然辩证法通讯, 2013, 35(4): 58-63. |
| [7] |
邓明立, 王淑红. 理想概念的历史演变(1801—1926)[J]. 自然辩证法通讯, 2003, 25(6): 78-83. DOI:10.3969/j.issn.1000-0763.2003.06.020 |
| [8] |
王淑红.交换环论的早期历史研究[D].西安: 西北大学博士学位论文, 2015: 29-38.
|
| [9] |
DEDEKIND R, WEBER H. Theorie der algebraischen Funktionen einer Veränderlichen[J]. Journal Reine Angew Math, 1882, 92: 181-290. |
| [10] |
LASKER E. Zur theorie der moduln und ideale[J]. Math Ann, 1905, 60: 20-116. DOI:10.1007/BF01447495 |
| [11] |
CORRY L. Modern Algebra and the Rise of Mathematical Structures[M]. Berlin: Birkäuser Verlag, 2004: 92-253.
|
| [12] |
MACAULAY F. S. On the resolution of a given modular system into primary systems including some properties of Hilbert numbers[J]. Math Ann, 1913, 74: 66-121. DOI:10.1007/BF01455345 |
| [13] |
BAKER H. F. Francis sowerby macaulay[J]. J London Math Soc, 1938, 13: 157-160.
|
| [14] |
BAKER H. F. Francis sowerby macaulay[J]. Obituary Notices of Fellows of the Royal Society of London Ⅱ (1936—1938), 1938, 357-361. |
 2017, Vol. 47
2017, Vol. 47