随着现代工业的发展, 在石油化工、能源动力、航空航天等众多领域中, 许多金属构件长期在高温、高压条件下服役, 不可避免地产生蠕变现象, 使得蠕变成为制约其完整性和安全运行的一个主要因素[1-2]。P91(9Cr-1MoVNb)马氏体耐热钢是以Cr, Mo为主要合金元素的马氏体合金钢, 在高温下具有较高的强度和抗氧化性, 以及良好的焊接性, 广泛应用于电力、核能以及石油化学工业等高温承压构件中[3], 特别是电厂主蒸汽管道及再热蒸汽管道热锻[4]。目前, 全世界已有的大量石油装置、化工厂、火电厂以及核电站等国家基础设施的许多关键设备的实际累积使用时间超过了30年, 国内部分电厂的关键部件更是超出其设计寿命但仍在服役。因此, 无论是从经济还是安全的角度来看, 对这些高温服役构件的健康状态评估和剩余寿命预测已经显得极为必要。
1 实验材料及方法 1.1 试验材料试验材料采用天津钢管集团股份有限公司生产的P91热轧钢管(母材规格为φ170mm×30mm), 化学成分见表 1; 其热处理工艺为:116℃正火(20min)→770℃回火(90min); 正火后为板条状马氏体组织, 高温回火后为回火马氏体组织。
|
|
表 1 P91钢化学成分 Tab. 1 Chemical component of P91 |
蠕变持久试验在长春机械科学研究院研发的高温蠕变试验机(RDL50)上完成, 试验以GB/T2039-1997为参照标准, 试样标距内的位移使用光栅测量, 电阻炉使用三段控温的方式来进行加热与保温, 加载前保温1h。
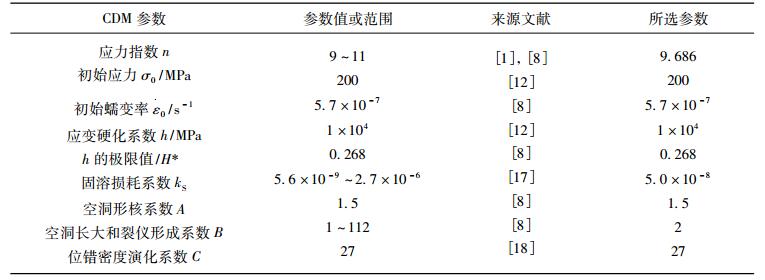
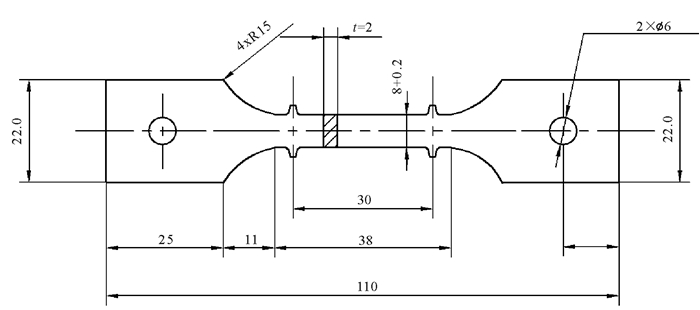
1.3 试验方法为保证试样形状精度和原始表面状态不受影响, 使用线切割的方式获得蠕变板材试样, 其几何尺寸如图 1所示。为了获得P91钢的高温拉伸性能(弹性极限、伸长率、断面收缩率、屈服强度、拉伸强度、弹性模量等), 首先进行了高温拉伸试验[5], 得到P91钢母材在600℃的高温拉伸曲线, 如图 2所示。根据图 2高温拉伸曲线, 可获得P91钢在600℃的常规机械性能, 其结果见表 2。
|
图 1 蠕变试样图 Fig. 1 Specimen of creep test |
|
图 2 P91钢600℃拉伸曲线 Fig. 2 Tensile curve of P91 steel at 600℃ |
|
|
表 2 P91钢600℃拉伸试验结果 Tab. 2 Tensile test results of P91 steel at 600℃ |
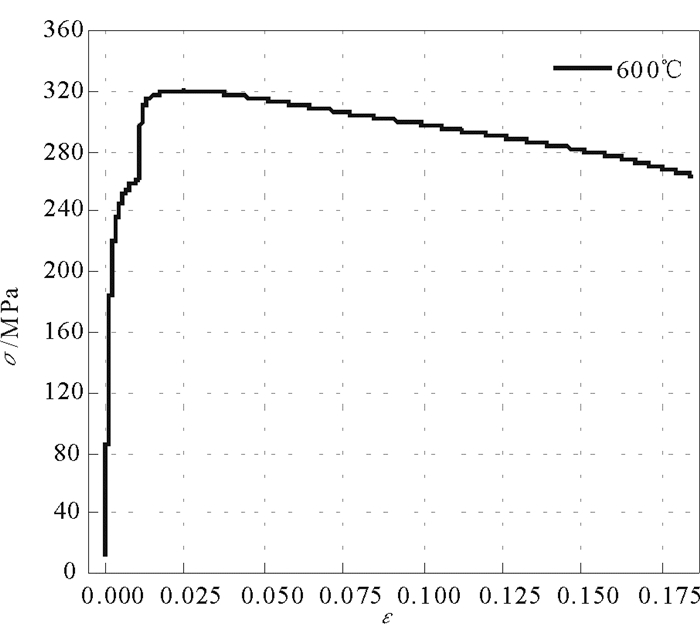
根据P91钢在600℃的高温拉伸结果, 分别在155, 160, 165, 175MPa完成蠕变持久试验, 其结果如图 3所示, 蠕变断裂时间tr见表 3。
|
图 3 P91钢600℃蠕变持久曲线 Fig. 3 Creep rupture curve of P91 steel at 600℃ |
|
|
表 3 P91钢600℃蠕变持久试验结果 Tab. 3 Creep rupture test results of P91 steel at 600℃ |
金属材料在给定温度(给定应力水平)下的蠕变变形机制可以根据变形机制图来确定[6]。P91马氏体耐热钢是一种第二相粒子弥散强化的合金材料[7], 根据其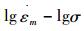
1) σ很小时, n=1, 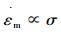
2) σ < σOrowan时, n=3~7, 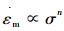
3) σ>σOrowan时, n=7~40, 此时, 位错按照Orowan机制绕过第二相粒子, 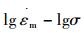
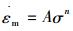
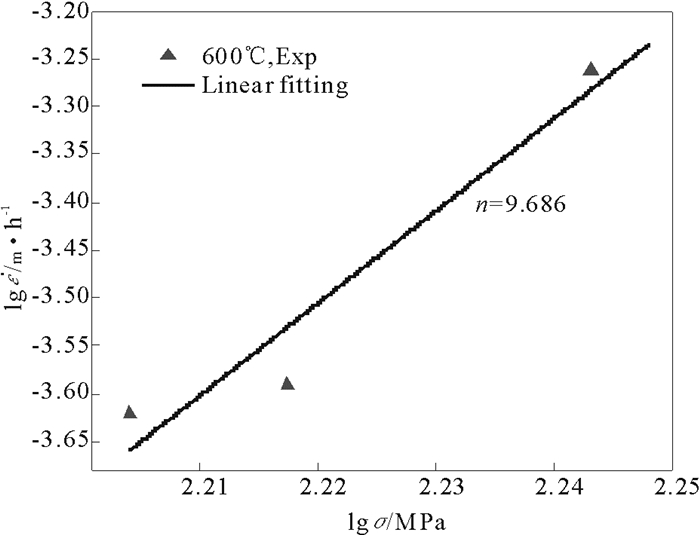
|
图 4 P91钢600℃时高应力范围内的lgσ与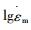 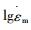 |
传统CDM模型由于具有明确的表达形式、能够耦合蠕变损伤各阶段的损伤参量、各损伤项具有明确的物理含义, 该模型具有较大的改进空间而成为近年来研究高温服役构件剩余寿命的有力工具。传统CDM模型中的多个损伤参量无法同时从物理机制上揭示材料蠕变损伤的实质和进一步改进蠕变损伤本构方程, 模型的数值求解也非常困难。Dyson[11]充分考虑了蠕变3个阶段的特征和各种损伤机制[6-9], 包括应变硬化、位错增值、溶质原子贫化、固溶损耗、第二相粒子(M23C6, MX, Laves相、Z相)粗化、空洞形核长大[12-14], 归纳总结了如下CDM本构方程:
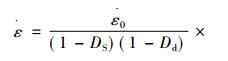
|
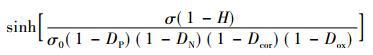
|
(1) |
式中:σ为外加应力; σ0为与位错-粒子交互作用有关的初始应力; 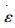
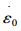
Basirat等人以位错演化动力学为基础[15], 将传统CDM模型与Orowan方程结合[16], 将CDM模型改进为如下形式(2)。该模型结果与试验数据吻合较好, 但该模型没有考虑到蠕变减速阶段和稳态阶段材料应变硬化的影响。Ghosh进一步改进传统CDM模型[17], 如式(3)所示。该模型能很好地拟合蠕变减速阶段和稳态阶段, 但在蠕变加速阶段出现较大偏差, 不能准确预测材料的蠕变断裂时间。其原因是该模型并没有考虑空洞形核长大与溶质原子贫化对材料蠕变过程的贡献和影响。
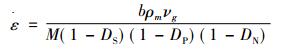
|
(2) |
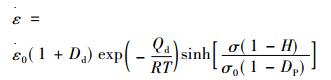
|
(3) |
式中: 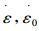
在这样的研究基础和前提下, 充分考虑P91钢在600℃高应力条件下的蠕变损伤机制, 本文提出另一种改进的CDM模型, 如式(4)所示。该模型整合了应变硬化、位错损伤、溶质原子贫化、第二相粒子粗化、空洞形核长大5项损伤参量。其最大的特点在于优化调整了位错损伤项, 充分考虑了位错萌生、增殖、湮灭等位错演化行为对材料蠕变行为的作用和影响。
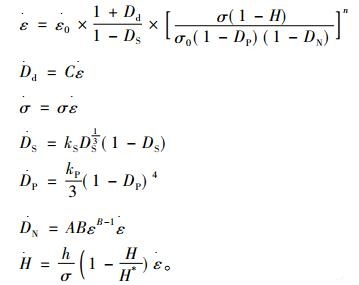
|
(4) |
式中:C为调节位错密度演变行为的模型参数; n为应力指数; H*, h, kS, kP, A, B均为材料常数; H*为表征材料蠕变过程中加工硬化的极限。
3 改进模型计算结果与讨论本文通过数值计算求解上述改进模型, 即常微分方程组(4)。将所得结果与试验数据对照, 其结果见图 5, 6。模型中使用的参数见表 4, 5。
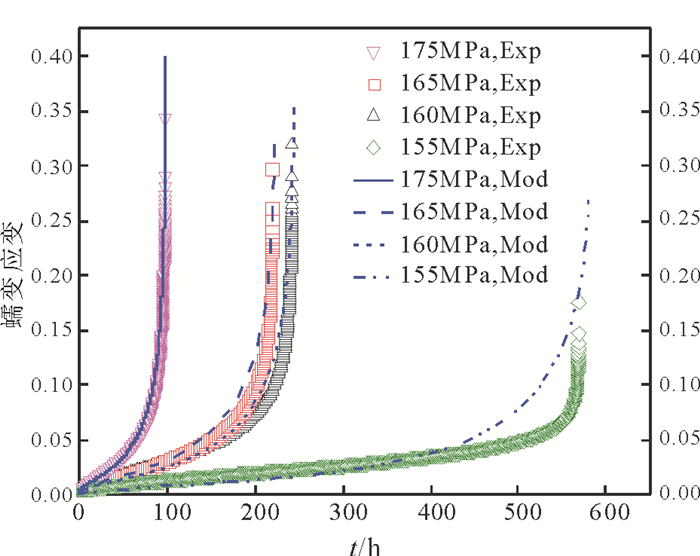
|
图 5 P91钢600℃不同应力条件下模型计算的蠕变应变与试验数据的对比 Fig. 5 Comparison between the model predictions and experimental data for the creep strains of P91 steel at 600℃ and stresses of 155MPa、160MPa、165MPa、175MPa |
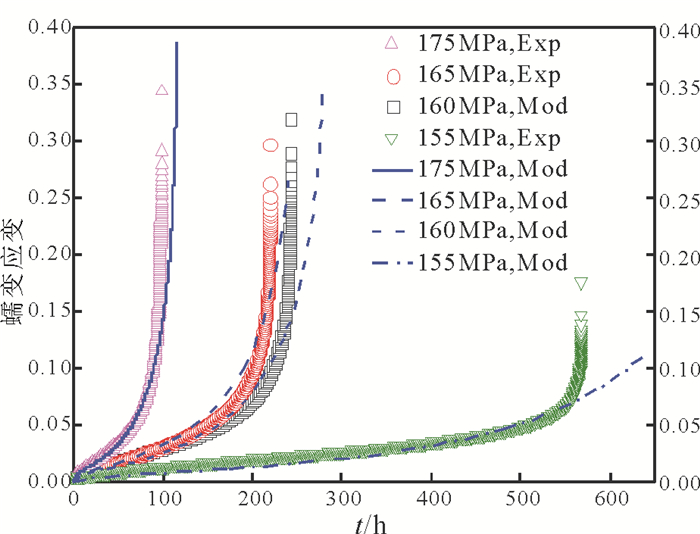
|
图 6 P91钢600℃不同应力条件下不考虑位错损伤项的模型计算结果与试验数据的对比 Fig. 6 Comparison between the model predictions without dislocation damage term and experimental data for the creep strains of P91 steel at 600℃ and stresses of 155, 160, 165, 175MPa |
|
|
表 4 改进CDM模型中使用的参数 Tab. 4 Modified CDM parameters value or range from literature and optimised parameters |
|
|
表 5 P91钢600℃时不同应力条件下第二相粒子粗化常数Kp的取值[17] Tab. 5 The value of the second phase particle coarsening constant under different stresses at 600℃ |
图 5为模型计算的蠕变应变结果与试验数据在600℃, 155, 160, 165, 175MPa应力下的对比结果; 图8为相同条件下, 不考虑位错损伤项Dd的模型计算结果与试验数据的对比。从图 7中可以看出, 在各个应力条件下的模型计算结果与试验数据吻合较好, 这说明本文改进的CDM模型具有一定的合理性和可靠性。在蠕变第三阶段的初期, 模型计算结果与试验数据有所偏差, 主要原因是该阶段空洞形核后快速长大, 微裂纹开始形成并快速长大导致试样发生断裂。特别是在155MPa应力下, 模型计算结果与试验数据在第三阶段初期发生较大偏离, 除了前述原因外, 另一个重要的影响因素是在155MPa应力下, 其蠕变断裂机制与其他3个应力有所不同, 蠕变断裂时间明显增长, 而试验是在600℃的高温下完成的, 不能不考虑温度的热时效作用对蠕变的贡献, 长期的热时效作用对蠕变第二相粒子的粗化行为有着重要的影响[18]。此外, 在该阶段, 随着蠕变应变的积累, 试样开始产生颈缩现象, 出现了局部应力集中的现象, 而试验数据是在恒应力条件下得到的。从图 6可以看出, 当不考虑位错萌生、增殖、湮灭等位错演化行为对材料蠕变行为的作用时, 数值模型的计算结果与试验数据吻合较差, 不同应力水平下模拟的蠕变断裂时间均长于试验结果, 155MPa应力下的结果尤为明显。
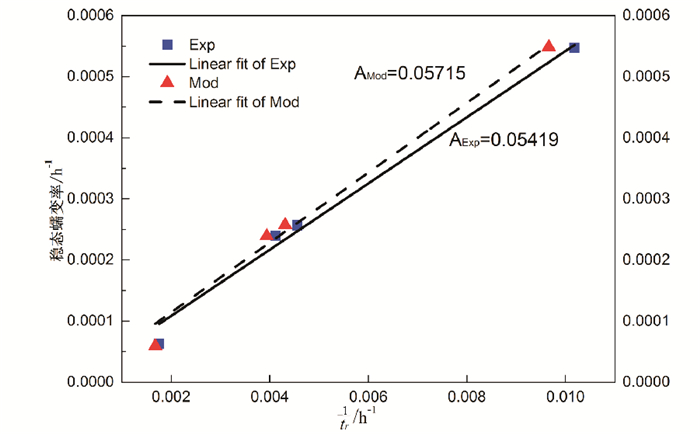
|
图 7 拟合模型与试验数据的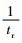 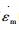 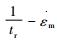 |
图 7为拟合改进CDM模型与试验数据的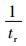
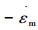
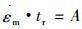
拟合结果为:Aexp=0.054 19, AMod=0.057 15。可以发现:Aexp≈AMod, 这说明该改进CDM模型可以预测P91钢在600℃, 155MPa~175MPa范围内的蠕变剩余寿命, 预测模型为: 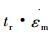
1) 获得了P91钢在600℃下的各项力学性能参数; P91钢在155, 160, 165, 175MPa应力下的单轴蠕变断裂时间分别为568.53h, 242.64h, 219.16h, 98.18h。
2) 通过调整耦合位错损伤项Dd, 改进传统CDM模型; 对比分析了改进模型中有无位错损伤项对蠕变剩余寿命的影响, 对比结果表明, 改进模型的数值计算结果与试验数据吻合较好, 说明本文提出的改进模型具有一定的合理性和可靠性。
3) 通过拟合本文提出的改进CDM模型与试验数据的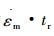
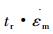
| [1] |
涂善东, 轩福贞, 王国珍. 高温条件下材料与结构力学行为的研究进展[J]. 固体力学学报, 2010, 31(6): 679-695. |
| [2] |
涂善东, 轩福贞, 王卫泽. 高温蠕变与断裂评价的若干关键问题[J]. 金属学报, 2009, 45(7): 781-787. DOI:10.3321/j.issn:0412-1961.2009.07.002 |
| [3] |
涂善东, 戴树和. 高温过程设备的寿命评价技术进展[J]. 压力容器, 1996(2): 151-158. |
| [4] |
郑善合.火力发电机组汽轮机高温部件变形及蠕变寿命的研究[D].北京: 华北电力大学, 2007.
|
| [5] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会.GB/T 228-2002金属材料室温拉伸实验方法[S].理化检验-物理分册.北京: 中国标准出版社, 2003.
|
| [6] |
ZHANG J S. High temperature deformation and fracture of materials[M]. 北京: 科学出版社, 2010.
|
| [7] |
章武媚. 高应力条件下T/P91钢蠕变行为仿真分析[J]. 铸造技术, 2014, 35(5): 884-886. |
| [8] |
陈云翔, 严伟, 胡平, 等. T/P91钢在高应力条件下蠕变行为的CDM模型模拟[J]. 金属学报, 2011, 47(11): 1372-1377. |
| [9] |
SHRESTHA T, BASIRAT M, CHARIT I, et al. Creep deformation mechanisms in modified 9Cr-1Mo steel[J]. Journal of Nuclear Materials, 2012, 423(1): 110-119. |
| [10] |
SHRESTHA T, BASIRAT M, CHARIT I, et al. Creep rupture behavior of Grade 91 steel[J]. Materials Science and Engineering: A, 2013, 565: 382-391. DOI:10.1016/j.msea.2012.12.031 |
| [11] |
DYSON B. Use of CDM in materials modeling and component creep life prediction[J]. Journal of Pressure Vessel Technology, 2000, 122(3): 281-296. DOI:10.1115/1.556185 |
| [12] |
PANAIT C G, BENDICK W, FUCHSMANN A, et al. Study of the microstructure of the Grade 91 steel after more than 100, 000 h of creep exposure at 600 C[J]. International Journal of Pressure Vessels and Piping, 2010, 87(6): 326-335. DOI:10.1016/j.ijpvp.2010.03.017 |
| [13] |
高加强, 王起江, 周冶东. P91耐热钢600℃短时蠕变行为探讨[J]. 物理测试, 2015, 33(4): 1-5. |
| [14] |
HALD J. Microstructure and long-term creep properties of 9%~12% Cr steels[J]. International Journal of Pressure Vessels and Piping, 2008, 85(1): 30-37. |
| [15] |
BASIRAT M, SHRESTHA T, POTIRNICHE G P, et al. A study of the creep behavior of modified 9Cr-1Mo steel using continuum-damage modeling[J]. International Journal of Plasticity, 2012, 37: 95-107. DOI:10.1016/j.ijplas.2012.04.004 |
| [16] |
OROWAN E. Problems of plastic gliding[J]. Proceedings of the Physical Society, 1940, 52(1): 8. |
| [17] |
GHOSH R N. Creep life predictions of engineering components: problems & prospects[J]. Procedia Engineering, 2013, 55: 599-606. DOI:10.1016/j.proeng.2013.03.301 |
| [18] |
WANG X, XU Q, YU Y U, et al. Laves-phase evolution during aging in 9Cr-1.8W-0.5Mo-VNb steel for USC power plants[J]. Materials Chemistry & Physics, 2015, 163: 219-228. |
 2017, Vol. 47
2017, Vol. 47