在基于统计模型的颅面复原中, 对颅面样本数据进行点对应操作是建立颅面统计模型中不可或缺的一个步骤, 而其对应结果的准确度也直接影响颅面复原的效果。这里的点对应是指:不同面皮模型上具有相同生理结构的点之间一一对应。由于面皮表面生理形态的复杂性和多样性, 对建立好点对应关系的面皮模型要求如下:面皮模型具有相等的顶点个数; 不同模型间相同序号的顶点位置具有生理一致性, 如样本A的第50个点是眉间点, 则样本B的第50个点也是眉间点; 样本需要配准到空间的同一位置, 避免仿射变换的影响。
目前, 已经有不少建立点对应的算法存在。基于网格重采样方法[1]是通过对三维人脸网格分片重采样实现点对应, 对应效果比较理想, 只是人为干预太多, 费时费力, 导致整个算法的运行效率不高; 基于欧氏距离的最近点对应[2]是通过计算模板面皮上待对应顶点到待对应面皮中所有顶点的欧氏距离, 求得最短距离的点, 建立一一对应关系, 然而, 当两个模型相对位置差距较大时会导致对应结果不稳定, 而且需要计算模板面皮上待对应顶点到待对应面皮的所有顶点的欧氏距离, 才能确定最近点, 大大增加了算法的时间复杂度; 还有基于运动的3D人脸全自动配准[3]、基于多视图关系的3D扫描配准(扩展的ICP)[4]、通过稀疏人脸变形建立点对应[5]以及文献[6]和[7]中所提非刚性配准方法等。上述方法都无法达到基于统计模型的颅面复原对准确度的要求。因此文中提出了基于体素模型与多尺度约束的三维面皮点对应方法。
1 3D面皮点对应方法的流程1) Frankfurt坐标系下进行面皮模型的坐标校正, 并根据MPEG-4对三维人脸动画格式定义的国际标准以及人脸形态特征, 为模板面皮标定72个人脸特征点;
2) 利用TPS(薄板样条函数)对待对应面皮模型进行变形, 使得待对应面皮与模板面皮形状近似重合;
3) 为面皮模型建立包含顶点的具有一阶邻接关系的体素模型, 可有效缩小对应点的搜索范围, 提高算法的执行效率;
4) 计算模板面皮体素模型中顶点的微分属性:平均法向和高斯曲率, 并按曲率的大小对顶点做递减排序;
5) 依次选取模板面皮中曲率值最大的顶点作为待对应点, 在法向、曲率以及凸多面体等多几何特征的共同约束下, 寻找待对应面皮到模板面皮的最佳匹配点。
2 Frankfurt坐标校正及特征点标定由于颅面模型数据库数据量大, 难免出现形态各异的样本数据, 为了避免对点对应算法造成影响, 这里将所有面皮模型统一到Frankfurt参考坐标系[8]下。该坐标系主要由面皮模型左耳孔、右耳孔、左眼眶下缘点和眉心4个点(Lp, Rp, Mp, Vp)确定。具体说明如下:
1) 直线LpRp与过Vp且以向量
2) 以点Lp和Rp所在直线作为X轴, 向量
3) 以过原点O且以向量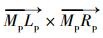
4) 以过原点O且垂直于XZ平面的直线作为Y轴, 方向根据右手法则可得。
通过以上步骤可画出Frankfurt坐标系定义图, 如图 1(a)所示, 面皮模型坐标校正后如图 1(b)所示。
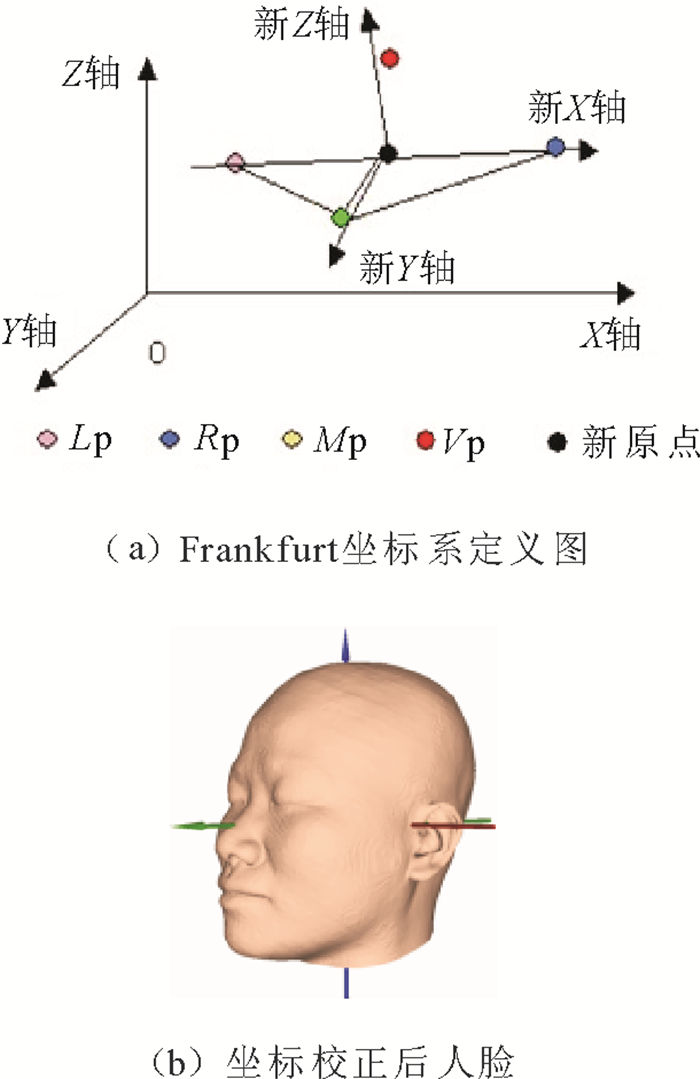
|
图 1 法兰克福坐标系 Fig. 1 Frankfurt coordinates |
由于重建出的单层面皮模型上有成千上万个顶点, 信息比较冗余, 不利于点对应算法的操作, 于是就提出了特征点标定的想法, 特征点的准确标定是实现面皮模型顶点一一对应的前提。特征点标定有手动标定、半自动标定以及全自动标定3种方法。文献[8]定义了39个特征点, 文献[9]和[10]分别实现了9个和10个颅骨特征点的自动标定, 然而, 上述方法中标定的特征点数目较少, 很难达到点对应算法对准确度的要求。目前, 大多数点对应算法采用的是手动标定法, 根据文献[8]以及人脸形态的特征, 文中为模板面皮标定了72个人脸特征点, 如图 2所示。
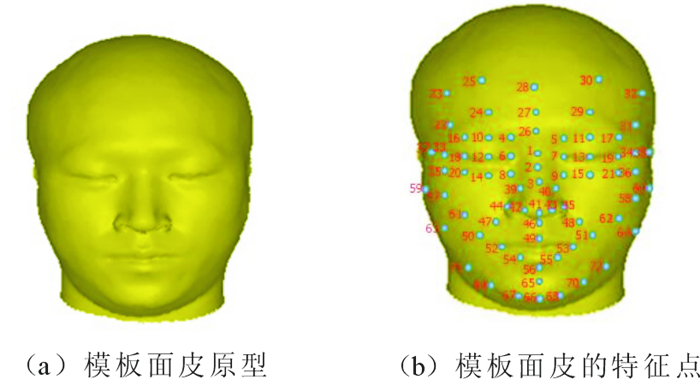
|
图 2 模板面皮特征点标定 Fig. 2 Feature points marking of model face |
径向基函数(RBF)是由多个基函数线性组合而成的一个多变量函数, 能够平滑地插值不规则分布的高维数据[11]。RBF的一般表示形式为
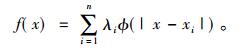
|
(1) |
其中, |·|表示二范数, 即欧氏距离, ϕ(·)表示基函数, xi表示当前特征点, n表示特征点的数目, n=72, λi表示与特征点xi对应的权重系数, 通过这72个特征点求得其最优值。
薄板样条函数(TPS)是径向基函数的一种。文中利用TPS对面皮模型变形是因为将薄片样条应用于径向基函数网络时通常对它附加一个线性多项式和薄板样条, 即
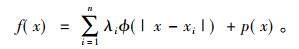
|
(2) |
其中, 仿射变换的线性多项式为p(x), 薄板样条为ϕ(r)=r2lg(r), r=|x-xi|, 而求解之后得到的基函数网络对应的线性项恰好对应特征点之间变换的仿射成分。因此, 薄片样条能够描述特征点分布的形状特征, 具有仿射不变性。采用该方法可在面皮模型间有效建立一个光滑其表面的插值函数, 可实现模型间的非刚性变形和近似重合。
4 基于体素模型与多尺度约束的点对应文中所涉及的多尺度特征包括体素化模型、法向、曲率以及凸多面体。
4.1 面皮模型体素化文中所说的体素化是指将三维面皮模型的几何表示形式转换成最接近该模型的体素表示形式, 产生体数据集, 其不仅包含模型的表面信息, 而且能描述模型的内部属性, 类似于二维的像素, 从二维的点扩展到三维的立方体单元。简言之就是从面模型(三角面片)转换为体模型(体素网格)称之为体素化。使用体素所表达的面皮模型简单稳定且不需要拓扑信息。
为面皮模型建立包含顶点的具有一阶邻接关系的体素模型, 可有效缩小模板面皮在待对应面皮中寻找对应点的搜索范围, 提高算法的执行效率, 因而在寻找点对应关系之前, 将面皮模型体素化处理。文中所用面皮模型均为单层数据模型, 降低了体素化模型处理的复杂度, 这里只需将面皮模型的所有三角网格表面做体素化处理, 可有效缩短整个点对应算法的时间复杂度。
面皮模型体素化方法具体步骤如下:
1) 根据读入的顶点数据, 分别计算模板面皮中所有顶点在X, Y, Z这3个坐标轴上的最大值Xmax, Ymax, Zmax和最小值Xmin, Ymin, Zmin;
2) 根据第一步求得的最大值和最小值, 分别计算在X, Y, Z方向上体元为4的体素个数Xnum=(Xmax-Xmin)/4, Ynum=(Ymax-Ymin)/4, Znum=(Zmax-Zmin)/4, 这里的体元指的是面皮网格模型中体素单元的边长, 实验结果表明, 当体元为4时, 点对应准确度更高, 所以这里体元设置为4, 则每个体素中通常只包含一个或不含网格顶点, 其优点是体素体积较小, 对包含其中的顶点的空间描述能力更强。由此可知, 文中体素是大小为4*4*4的立方体;
3) 建立体素化结构体

|
(3) |
其中, x, y, z域为数组, 保存当前体素中包含顶点的坐标(可能不止一个点), voxNum域为数组, 保存体素所含顶点的序号, adjVer域为元胞数组, 每行只有一个元胞, 对应保存相应voxNum数组的行号一阶邻接点, 初始化为空;
4) 利用模板面皮的每个顶点的坐标求出其X, Y, Z这3个方向上的体素单元的序号, 如当前点坐标为(x, y, z), 则其X方向上的体素单元的序号为i=ceil(x-Xmin)/4, Y方向上的体素单元的序号为j=ceil(y-Ymin)/4, Z方向上的体素单元的序号为k=ceil(z-Zmin)/4。其中, ceil是Matlab的函数, 表示向上取整; 然后将当前点序号及其坐标存入索引为(i, j, k)的体素单元中;
5) 根据读入的面数据, 即图 2中的三角网格模型, 将包含当前顶点(x, y, z)的所有面上的其余两个顶点序号存入体素索引为(i, j, k)的adjVer域中, 建立每个顶点的一阶邻域关系。
通过上述步骤构造出来的体素模型操作简单, 可以方便快捷地获取顶点的一阶邻域信息, 可有效约束模板面皮待对应顶点在待对应面皮中寻找对应点的搜索范围, 降低了算法的时间复杂度, 最重要的是剔除了点对应过程中模板面皮的当前顶点在待对应面皮中不可能成为待对应顶点的一些点, 避免了严重错配的情况发生。图 3为面皮模型局部体素化后效果图, 图 3(a)为鼻子原始模型, 图 3(b)为体素模型。

|
图 3 面皮模型鼻部体素化效果 Fig. 3 Nose voxelization of model face |
面皮模型顶点法向量的计算有很多方法, 文中根据体素化过程中获得的顶点的一阶邻域信息, 采用当前顶点vi的一阶邻接域的法向量关于邻接三角形面积和角度的加权平均方法来计算法向量, 利用体素化模型关于当前顶点的一阶邻域关系, 有效约束法向的计算。顶点vi的一阶邻域如图 4所示。

|
图 4 顶点vi的一阶邻接域 Fig. 4 First order int adjvex of vertex vi |
顶点vi平均法向量计算公式为

|
(4) |
其中, n表示顶点vi的邻接三角面片个数, Sfk为顶点vi的第k个邻接三角面片的面积,
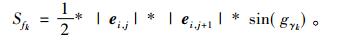
|
(5) |
其中, gγk为顶点vi与其邻接顶点vj和vj+1所组成的向量ei, j和ei, j+1的夹角, 引入角度的原因是度数越大, 则第k个三角面片占的权重就比较大, grk用式(6)求得,
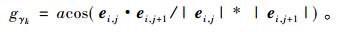
|
(6) |
nfk为顶点vi的第k个邻接三角面片的法向,
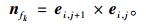
|
(7) |
三角网格曲面的离散曲率估算有多种方法, 有基于改进Voronoi区域面积的Mark Meyer曲率估算方法[12]和逆向工程中离散曲率的估算与可视化[13]等, 文中针对面皮的三角网格模型, 以Meyer等提出的Voronoi方法[14]为基础, 计算顶点的高斯曲率K。该方法的基本思想是把光滑曲面看作是一族网格的线性逼近, 将三角网格中每个顶点的度量性质视为其体素模型一阶邻域的平均度量。顶点vi的高斯曲率计算公式为
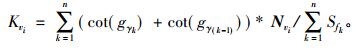
|
(8) |
分两种情况讨论:若第k个邻接三角形是锐角三角形, 则取三角形的外心连接除顶点vi对边以外的两条边vi, j和vi, j+1的中点, 得到新的面积Sfk,

|
(9) |
其中, ofk为第k个邻接三角形的外心坐标; 若第k个邻接三角形是钝角三角形, 则Sfk为

|
(10) |
若顶点vi的当前邻接边vi, j被两个邻接三角面片fk与fk-1所共用, 则计算两个三角面片关于顶点vi的夹角, 计算公式为

|
(11) |

|
(12) |
文中将模板面皮用Mf表示, 待对应面皮用Uf表示, 根据第2节中所说, 首先, 对Mf和Uf进行Frankfurt坐标校正, 并对Mf进行特征点的标定; 然后对Uf进行TPS变形, 使其与Mf近似重合; 最后基于多几何特征的约束建立Mf和Uf之间的点对应关系。具体操作如下:
1) 面皮模型体素化。对Mf和Uf进行体素化, 生成体素模型, 分别用Mv和Uv表示, 如式(3)中的体素模型的结构体, 存储了每个顶点的一阶邻域, 在搜索点对应关系时, 可以快速获取顶点的邻接关系, 缩小了待对应点寻找对应点的搜索范围, 为了后面凸多面体的约束条件, 这里需要计算Mf中每个顶点的二阶邻域, 用adj-2表示;
2) 计算法向和曲率。利用公式(4)和(8)分别计算Mv和Uv中每个顶点的微分属性:平均法向和高斯曲率, 并按Mf中曲率的大小对顶点作递减排序;
3) 确定搜索范围。依次选取Mf中曲率值最大即特征最明显的顶点作为当前待对应点, 记为v, 计算该点在其X, Y, Z这3个方向的体素单元的序号, 并利用体素号求出顶点v在3个方向的最大最小值, 根据最大最小值确定顶点v在Uv中的体素序号(体素序号大小因待对应面皮的体素模型大小而异, 文中体素序号最大是6), 最后确定顶点v在Uv中的搜索范围, 用search表示;
4) 确定点对应关系。根据第3步中确定的搜索范围search, 在Uv中展开寻找Mv中当前待对应顶点v的对应点。依次对search中体素进行搜索, 在Uv中寻找对应的体素序号, 获得该体素序号中的所有顶点, 然后在这些顶点中找出最佳对应点。首先, 第1步提到的二阶邻域adj-2是用来加强约束, 判断Uv中待判断点是否在凸多面体中, 即相应的面的里方向, 若在, 求得Mv中当前待对应顶点v和Uv中所对应体素号中的顶点vx的法向夹角, 用θ表示, 若θ < π/4, 则根据公式

|
(13) |
计算模板顶点v与vx的法向和曲率的加权距离。其中, α表示曲率权重(α=0.7), ||·||表示欧氏距离。循环进行上述操作, 直至找到Mv中当前待对应顶点v与在Uv中对应体素序号的点vx之间最短D(v, vx)的顶点, 即为最佳对应顶点, 从而确定最佳对应关系。
由以上4个步骤可看出, 为Mf中的顶点寻找生理一致对应点时, 是通过基于多尺度约束完成的。通过面皮模型体素化可缩小待对应搜索范围; 经过凸多面体约束可进一步排除不满足条件的候选点; 最后再根据平均法向和高斯曲率的共同作用, 完成待对应点的最佳匹配。其中, 计算法向量时考虑角度的因素, 即每个三角面片所占比重; 计算曲率时考虑到钝角和锐角三角面片的差异, 采用不同公式来计算, 这些都是为了能够最终提高点对应准确度。
5 实验结果分析根据文中所提出的3D面皮点对应算法, 进行编程实现。首先在面皮样本数据库中随机抽取30套数据, 建立它们的单层面皮模型, 作为实现点对应算法的测试数据集, 利用所设计点对应系统建立模板面皮和待对应面皮间的点对应关系。
5.1 结果分析基于文中所提出的算法进行实验, 结果如图 5所示, 从不同视角展示了面皮模型五官区域的点对应效果。其中, 图 5(a)的左侧为Mf, 右侧为Uf, 图 5(b)的下方为Mf, 上方为Uf, 从图中可看出, 用线作为两个模型彼此相对应点的连接。

|
图 5 模板面皮与待对应面皮点对应结果图 Fig. 5 Points corresponding results of model face and unknown face |
图 6展示了模板面皮与待对应面皮局部点对应的效果, 其中, 图 6(a)和(b)分别是鼻子部分与嘴巴和下巴部分的局部点对应示意图。

|
图 6 模板面皮与待对应面皮局部点对应结果 Fig. 6 Local points corresponding results of model face and unknown face |
采用两种点对应方法与文中所提出方法作对比实验, 对同一测试样本, 在3种算法下分别建立生理一致点对应关系, 其局部区域的对应结果如图 7所示。

|
图 7 不同方法建立模板面皮与测试面皮局部点对应效果对比 Fig. 7 The comparison for the different methods to establish local points corresponding of model face and testing face |
图 7(a)采用文中方法, 图 7(b)和图 7(c)分别是采用基于欧氏距离的最近点对应方法[2]和基于曲率与法向加权距离的最小点对应方法建立的点对应关系。图 7(c)所用方法与文中方法有类似的地方, 是为了突出体现模型体素化之后, 考虑各方面因素求得平均法向和高斯曲率进行点对应的准确度和效率的, 是为了对比文中所提出的方法。从图中可以看出, 图 7(a)中的鼻子区域, 不管是鼻尖还是鼻翼都满足局部点对应关系生理一致性的要求, 鼻尖点对应鼻尖点, 鼻翼点对应鼻翼点。相对而言, 图 7(b)和图 7(c)中可以明显看到鼻翼的某些顶点并没有找到生理一致的准确对应点, 鼻翼点对应到了鼻尖点上, 出现了错配现象。
为了更加直观地对比这3种方法, 对随机抽取的30套测试样本, 分别采用3种方法建立点对应关系, 并根据实验结果, 统计正确点对应的个数, 计算3个算法的平均准确率, 如表 1所示。平均准确率用ζ表示,
|
|
表 1 不同方法建立点对应关系的平均准确率 Tab. 1 Average accuracy of different methods to establish local points corresponding |

|
(14) |
其中, p表示测试样本的个数, P表示模板面皮的顶点个数, Pi表示模板面皮与第i个测试面皮的正确点对应的个数。
分析图 7和表 1的3种方法可知, 采用基于欧氏距离的最近点对应方法寻找生理一致对应点的过程比较单一, 此方法主要是根据欧氏距离最小确定对应点, 即需要计算模板面皮中的待对应顶点到待对应面皮中所有顶点的欧式距离, 然后取距离最短的作为其对应点, 这个计算过程十分费时, 大大增加了算法的时间复杂度, 而且对待对应顶点没有筛选性, 容易出现错配现象, 又由于3D面皮模型脸部的凹凸性和复杂性, 导致了此方法点对应结果的不稳定; 采用基于曲率与法向加权距离最小的点对应方法寻找生理一致对应点的过程也比较简单。此方法主要是计算曲率和法向, 并根据曲率与法向的加权距离确定对应点, 即需要计算面皮模型中所有顶点的曲率、法向以及模板面皮中的待对应顶点到待对应面皮中所有顶点的曲率和法向的加权距离, 然后取距离最短的作为对应点。这个计算过程与采用基于欧氏距离的最近点对应方法一样费时, 又由于面皮模型局部几何特征的相似性, 法向和曲率的几何约束条件太少, 也不利于提高点对应的准确度, 导致了此方法点对应结果的准确度较低。而文中采用基于体素模型、平均法向、高斯曲率以及凸多面体等多尺度约束的点对应算法, 不仅有效缩小了模板面皮中待对应顶点在待对应面皮中寻找对应点的搜索范围, 提高了搜索效率, 降低了时间复杂度, 而且保证了局部区域生理一致点对应的稳定性, 不会因为面皮模型差异较大而严重影响点对应的准确度。经过实验证明, 在模板面皮和待对应面皮相同的情况下, 分别采用这3种方法寻找对应点, 基于欧氏距离的最近点对应方法与基于曲率与法向加权距离最小的点对应方法的执行时间是文中方法平均耗时的5倍之余。
6 结语文中提出的基于体素模型与多尺度约束的三维面皮点对应算法, 在面皮TPS变形的基础上, 通过面皮模型体素化、计算顶点微分属性以及在凸多面体的多尺度约束下, 完成模板面皮与待对应面皮的生理一致点对应, 并与已有方法做对比实验。实验结果表明:该算法有效提高了点对应的准确度, 且降低了算法运行时间。
| [1] |
胡永利, 尹宝才, 谷春亮, 等. 基于形变模型的三维人脸重建方法及其改进[J]. 计算机学报, 2005, 28(10): 1671-1679. DOI:10.3321/j.issn:0254-4164.2005.10.013 |
| [2] |
CHEN J H, ZHENG K C, SHAPIRO L G. 3D point correspondence by minimum description length in feature space[C]//Proceeding of the 11th European Conference on Computer Vision, Springer Berlin Heidelberg, 2010: 621-634.
|
| [3] |
BOLKART T, WUHRER S. 3D faces in motion: Fully automatic registration and statistical analysis[J]. Computer Vision and Image Understanding, 2014, 131: 100-115. |
| [4] |
GOVINDU V M, POOJA A. On averaging multiview relations for 3D scan registration[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1289-1302. DOI:10.1109/TIP.2013.2246517 |
| [5] |
PAN Gang, ZHANG Xiaobo, WANG Yueming, et al. Establishing point correspondence of 3D faces via sparse facial deformable model[J]. IEEE Transactions on Image Processing, 2013, 22(11): 4170-4181. DOI:10.1109/TIP.2013.2271115 |
| [6] |
MA Jiayi, ZHAO Ji, MA Yong, et al. Non-rigid visible and infrared face registration via regularized gaussian fields criterion[J]. Pattern Recognition, 2014, 48(3): 772-784. |
| [7] |
CHEN Jun, MA Jiayi, YANG Changcai, et al. Non-rigid point set registration via coherent spatial mapping[J]. Signal Processing, 2015, 106: 62-72. DOI:10.1016/j.sigpro.2014.07.004 |
| [8] |
李康.基于颅骨的人脸建模技术研究及在法医面貌复原中的应用[D].西安: 西北大学, 2006, 24-28.
|
| [9] |
刘晓宁, 周明全. 高原一种自动标定颅骨特征点的方法[J]. 西北大学学报(自然科学版), 2005, 35(3): 258-261. DOI:10.3321/j.issn:1000-274X.2005.03.004 |
| [10] |
冯筠, 陈雨, 仝鑫龙, 等. 三维颅骨特征点的自动标定[J]. 光学精密工程, 2014, 22(5): 1388-1394. |
| [11] |
张磊.基于径向基函数的三维形状分析、变形与动画研究[D].北京: 北京大学, 2005, 21-24.
|
| [12] |
李谦, 徐永安, 马骁, 等. 基于改进Voronoi区域面积的MarkMeyer曲率估算方法[J]. 计算机与现代化, 2014(8): 26-29. DOI:10.3969/j.issn.1006-2475.2014.08.006 |
| [13] |
LIU Pengxin, WANG Yang, LIU Xuan. Discrete curvature estimation and visualization in reverse engineering[J]. Modern Manufacturing Engineering, 2011, 32(2): 15-18. |
| [14] |
MEYER M, DESBRUN M, SCHRÖDER P, et al. Discrete differential geometry operators for triangulated 2-manifolds[M]//Visualization and Mathematics, Springer Berlin Heidelberg, 2003: 35-57.
|
 2017, Vol. 47
2017, Vol. 47
