2. 福建工程学院 信息科学与工程学院, 福州 350118
2. School of Information Science and Engineering, Fujian University of Technology, Fuzhou 350118, China
近年来, 随着我国电力系统联网的规模越来越大, 解决了能源分布地与用电地区矛盾的同时, 电力系统的低频振荡事件也时有发生。如果不能及时采取正确的应对措施, 其危害不言而喻, 是系统稳定运行的重大潜在隐患[1-3]。目前, 电力系统稳定器是一个方便有效的办法用来抑制电网中的低频振荡。
PSS参数的设计方法最早是由DeMello提出的相位补偿法。其他的方法还有极点配置法, 留数相位补偿法[4]等, 这些方法也都是从相位补偿法发展而来的[5]。还有后来研究人员引入一些仿生智能算法[6]来设计PSS参数, 有诸如遗传算法[7]、粒子群算法[8-9]等。但智能算法需要建立问题的模型, 这对于庞大的电力系统是几乎不可能的, 即使建立了模型, 智能算法所需时间也是比较长的。
PSS的超前相位是补偿励磁系统的滞后相位[10-11], 需要测量励磁系统的无PSS补偿时的滞后特性, 而且励磁系统的滞后相位是随现场工况条件而有不同的差异。而滞后特性传统的测量方法是需要通过在线激励方法测得[12], 这可能会对系统稳定性造成危害。针对这一问题, 文中提出了一种基于现场实测扰动数据来设计PSS参数的新方法, 不需人为地施加外在干扰, 方便易操作, 不对实际的电力系统产生危害。
文中在深入分析了以Heffron-Philips为基础的负阻尼机理产生的低频振荡原因, 并着重理清该理论模型下各状态变量的相位关系, 理论推导了其与励磁系统滞后相位之间的联系, 试图从各状态变量的相位关系近似地求出励磁系统滞后相位, 为PSS相位补偿提供依据。此外, 也研究了PSS增益参数的设计, 目的是使产生的正阻尼转矩大小合适, 使系统中的弱阻尼振荡模式或欠阻尼振荡模式能够得到抑制, 满足电力系统稳定运行时振荡阻尼比不小于0.05的要求[13-15]; 同时也不显著恶化系统存在其他的振荡模式。仿真实验结果分析表明, 基于现场实测扰动数据的电力系统稳定器参数的设计能够有效抑制电力系统低频振荡。
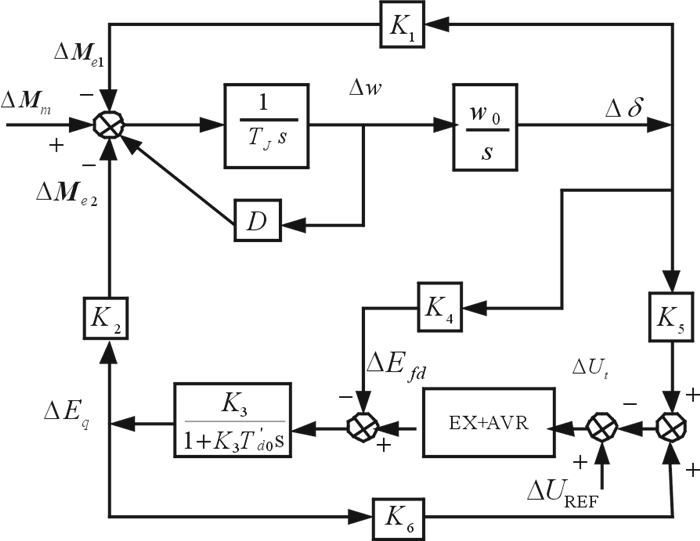
1 励磁系统滞后特性图 1为发电机的Heffron-Philips模型框图。该模型认为发电机的转子惯性环节决定了机电振荡的振荡频率, 而将励磁系统对发电机的作用等效分解为附加阻尼转矩和同步转矩。低频振荡通常属于小干扰稳定性分析的范畴, 在发电机工作点处线性化处理。大量的文献推导了发电机的三阶模型, 得出快速励磁系统提供的阻尼转矩方向与系数K5正负有关。当K5为正数时, 励磁系统能够提供正阻尼转矩, 增强系统的运行稳定性; 当K5为负数时, 励磁系统能够提供负阻尼转矩, 则系统有可能发生低频振荡。
|
图 1 发电机模型 Fig. 1 Generator model |
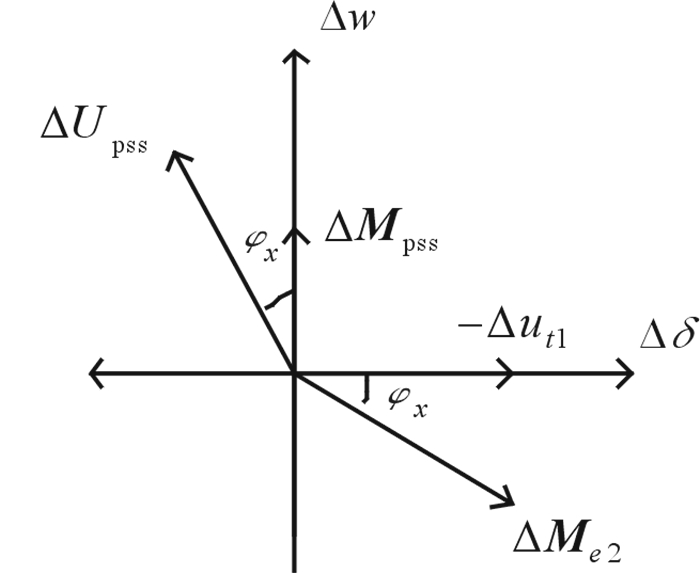
图 2为K5为负数时, 励磁系统产生了一个滞后于Δδ方向φx角度的附加转矩ΔMe2, 此时ΔMe2按Δδ和Δw组成的正交坐标系分解得到的阻尼转矩与Δw方向相反, 不利于系统稳定。现代电力系统为提高其静态电压稳定性, 通常发电机大都采用了快速高放大倍数的电压调节器, 但同时也存在电压调节器对转速变化反调的情况, 且当系统在处于远距离输电和高负荷运行状态时, K5很有可能为负, 易诱发系统低频振荡, 不利于系统的稳定运行。
|
图 2 阻尼转矩矢量图 Fig. 2 Damping torque vector |
针对电压调节器输出在快速励磁系统的作用下, 存在给系统带来附加负阻尼转矩的可能性, PSS设计的便是基于相位补偿原理通过引入一个附加信号ΔUpss, 产生一个正比与转速变换的附加正阻尼转矩ΔMpss, 可抵消电压调节器的阻尼转矩, 抑制系统低频振荡, 提高系统运行的稳定性。
对于励磁系统的滞后特性, 与高放大倍数Ka相比, K4很小, 其影响很小, 通常可以忽略。为证明这一点, 对于单机系统参数如下:K1=1.075 5, K2=1.257 8, K3=0.307 2, K4=1.712 4, K5=-0.040 9, K6=0.497 1, Ka=200, Te=0.001, T′d0=8。考虑K4影响和忽略K4影响分别得到的励磁系统滞后的相频特性曲线如图 3所示。可以看出对于快速、高放大倍数的电压调节器来说, 两种情况下的相频特性曲线基本重合, 说明K4对励磁系统的相频特性影响很小, 可以忽略。

|
图 3 励磁系统相频特性 Fig. 3 Phase-frequency characteristics of excitation system |
从图 1可以看出, 励磁系统滞后相角φx为从功角增量Δδ为输入到暂态电动势增量ΔE′q为输出之间的相角差, 根据K5的符号, 有两种情况,
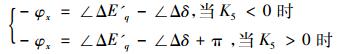
|
(1) |
励磁电压增量ΔEfd经过发电机的励磁绕组作用后得到暂态电动势增量ΔE′q,
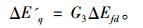
|
(2) |
其中, G3为发电机励磁绕组系统传递函数,
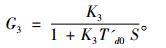
|
(3) |
由式(2)得到两者之间的相位关系,
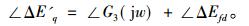
|
(4) |
只有电压调解器而无PSS补偿时, 励磁电压输入增量-ΔUt经过励磁调节器输出为励磁电压增量ΔEfd,
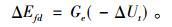
|
(5) |
其中, 快速励磁调节器系统传递函数为
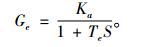
|
(6) |
所以有
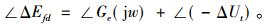
|
(7) |
快速励磁系统的励磁时间常数通常很小, 当励磁时间常数Te=0.001时, 快速励磁调节器系统传递函数的相频特性中ΔEfd相位与-ΔUt相位基本一致。
功角和转速之间的微分方程为
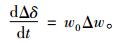
|
(8) |
由式(8)可得转速增量Δw与功角增量Δδ之间的相位关系为
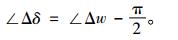
|
(9) |
当K5 < 0时, 将式(4), (7), (9)代入式(1),
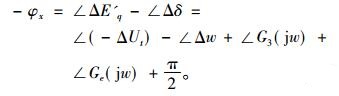
|
(10) |
同理, 当K5>0时, 有
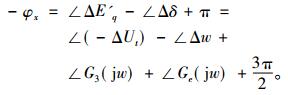
|
(11) |
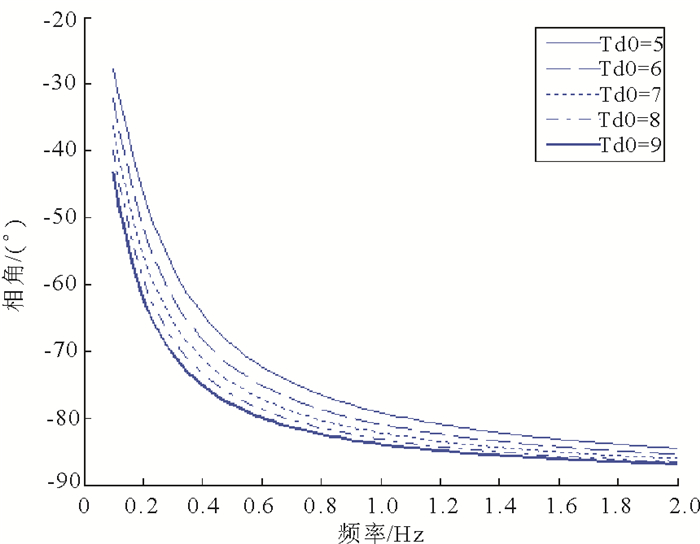
图 4为K3=0.167时, 励磁绕组时间常数T′d0为不同取值时的发电机励磁绕组系统相频特性曲线。
|
图 4 发电机励磁绕组系统的相频特性 Fig. 4 Phase-frequency characteristics of generator excitation winding system |
从图 4可以看出, 通常在低频振荡0.2Hz~2.0Hz的频率范围, 发电机励磁绕组系统传递函数G3的相位滞后大约为90°, 快速励磁调节器的滞后相角约为0°。简化处理, 励磁系统滞后角可以根据转速增量Δw和端电压增量ΔUt之间相位关系求得, 如式(12)所示:
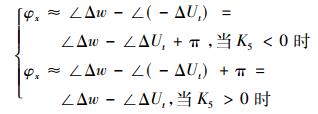
|
(12) |
在高频段滞后角φx偏大几度, 在低频段偏大十几度。而PSS补偿相位的要求一般是在-30°~30°之间, 即可以满足要求。
2 PSS的增益K设计无PSS时系统特征方程为
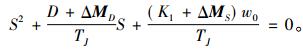
|
(13) |
解特征方程得到衰减指数α0为
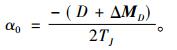
|
(14) |
在振荡角频率wd处
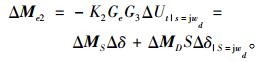
|
(15) |
将电压调节器产生的附加阻尼转矩ΔMe2分解为阻尼转矩和同步转矩两个方向。
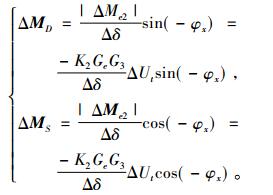
|
(16) |
若以Δw作为PSS的附加信号, 在振荡频率wd处补偿角度设为φ, 则其产生的附加阻尼转矩为
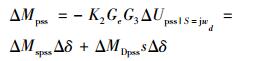
|
(17) |
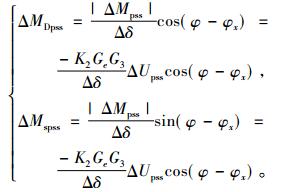
|
(18) |
则此时的衰减系数为
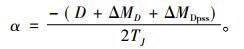
|
(19) |
假设加入PSS后振荡角频率不变, 仍然为wd。未装PSS时的阻尼比ζ0为
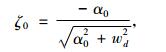
|
(20) |
装PSS时的阻尼比ζ为
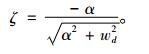
|
(21) |
式(20)与式(21)相比得到
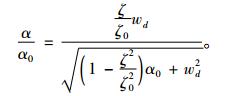
|
(22) |
定义k为
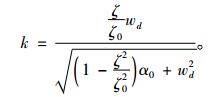
|
(23) |
则附加信号Δw产生的阻尼转矩ΔMDpss为
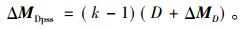
|
(24) |
若D=0, 则
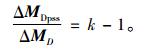
|
(25) |
将式(16)和(18)代入式(25)得
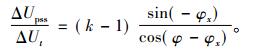
|
(26) |
由于PSS的传递函数为Gpss, PSS输入的附加信号Δw与输出ΔUpss之间的关系为
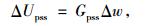
|
(27) |
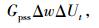
|
(28) |
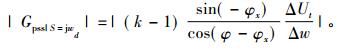
|
(29) |
所以根据式(29)可以进一步设计PSS的增益K。
3 PSS参数设计步骤由上述对电力系统产生低频振荡负阻尼的机理分析, 并结合励磁系统的滞后特性, 文中提出的励磁系统滞后特性的电力系统稳定器参数设计方法步骤如下:
1) 根据TLS-ESPRIT算法分析得到系统主导低频振荡模式, 再由现场实测扰动状态数据按式(12)计算得到该振荡模式下励磁系统滞后相位和端电压变化幅值/角速度变化幅值。
2) 设定PSS参数使得PSS向发电机提供正阻尼转矩, 且参数满足式(30), 若给定T2和T4的值, 便可求得T1和T3, 其中φ1与φ2可自由选择。
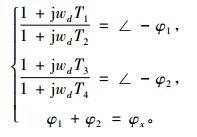
|
(30) |
3) 最后由式(29)确定PSS的增益K的值。
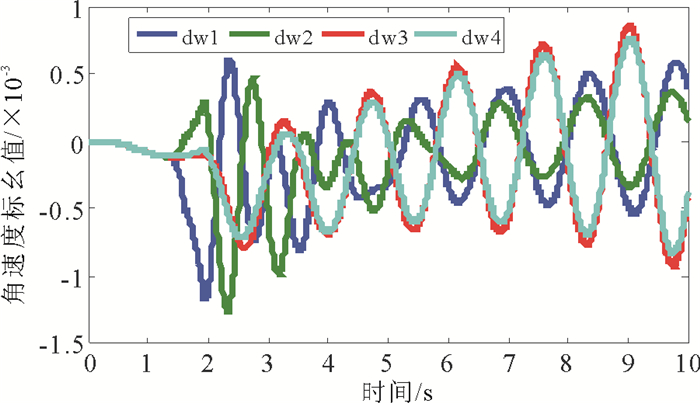
4 仿真实验与分析对于4机2区域系统, 运行方式为由机1和机2组成的区域1向由机3和机4组成的区域2传输413MW的功率。在未装PSS时, 将幅值为0.05的方波脉冲施加在发电机1的励磁参考电压上, 干扰信号的作用时间为1~1.1s, 此时受到干扰的系统发生了低频振荡, 如图 5所示, 给出了4机转速变换曲线。
|
图 5 四机转速变化曲线图 Fig. 5 Rotating speed curves of four generators |
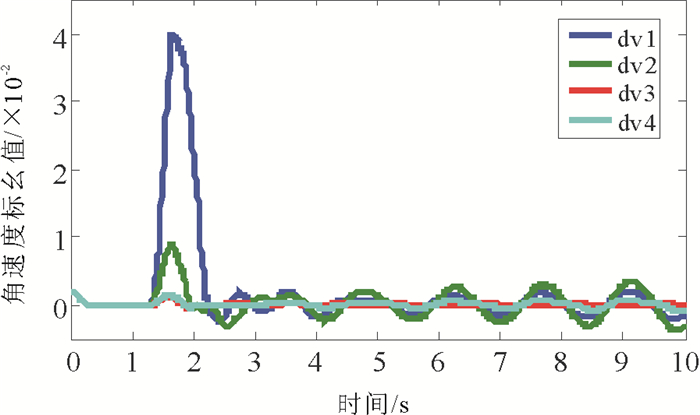
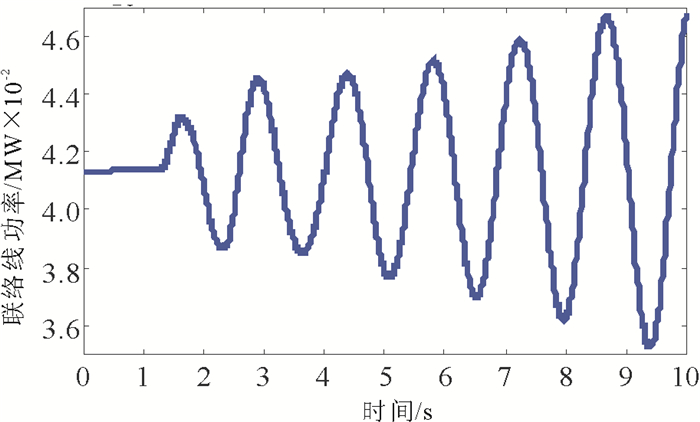
图 6给出了4机端电压变化曲线, 由于发电机1受到方波信号的干扰, 所以有一个很大的尖峰电压。图 7给出了联络线传输功率曲线, 很明显系统发生了区间振荡, 且为发散型的振荡, 系统不稳定。
|
图 6 四机端电压变换曲线图 Fig. 6 Terminal voltage curves of four generators |
|
图 7 联络线传输功率曲线图 Fig. 7 Transmission line power curve |
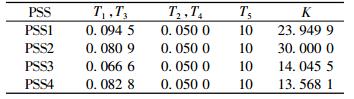
PSS是常用的抑制低频振荡的手段, 包括增益环节、隔直环节、两个相位补偿环节和限幅环节。在设计4台发电机的PSS参数时, 隔直时间常数T5取10, 限幅在-0.15~0.15之间, 固定其中T2, T4都为0.05, K值限制在30以内。按期望阻尼比0.15设计。首先按留数法设计PSS参数, 其设计方法是首先辨识算法求得系统传递函数, 再按一定的阻尼比设计。求得的各PSS参数如表 1所示。
|
|
表 1 四机的PSS参数 Tab. 1 PSS parameters of four generators |
按表 1给出的参数设计各PSS, 系统在施加同样条件的干扰情况下, 其运行结果如图 8所示。实验结果说明按留数法设计PSS参数能够抑制系统低频振荡, 保障系统稳定运行。
|
图 8 加入留数法设计的PSS后系统转速和功率曲线 Fig. 8 System speed and power curve with residue method |
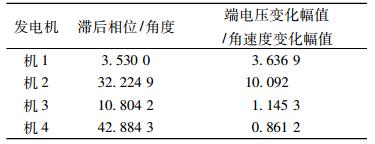
按本文的新方法设计PSS。首先用TLS-ESPRIT方法分别对同一时间段的4机转速变化曲线和4机端电压曲线进行分析, 可以发现系统发生了振荡频率为0.64Hz, 阻尼比为-0.026的负阻尼区间振荡模式, 系统不稳定, 需要配置PSS来抑制低频振荡。根据TLS-ESPRIT算法分析得到的结果, 表 2给出的按式(12)计算得到的振荡频率为0.64Hz时的励磁系统滞后相位和端电压变化幅值/角速度变化幅值。
|
|
表 2 振荡频率为0.64Hz的励磁系统滞后相位 Tab. 2 Hysteresis phase of excitation system with oscillation frequency of 0.64Hz |
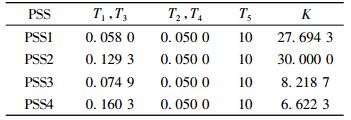
在设计4台发电机的PSS参数时, 同样隔直时间常数T5取10, 限幅在-0.15~0.15之间, 固定其中T2, T4都为0.05, K值限制在30以内, 按期望阻尼比0.15设计。表 3给出了各PSS求得的设计参数。
|
|
表 3 四机的PSS参数 Tab. 3 PSS parameters of four generators |
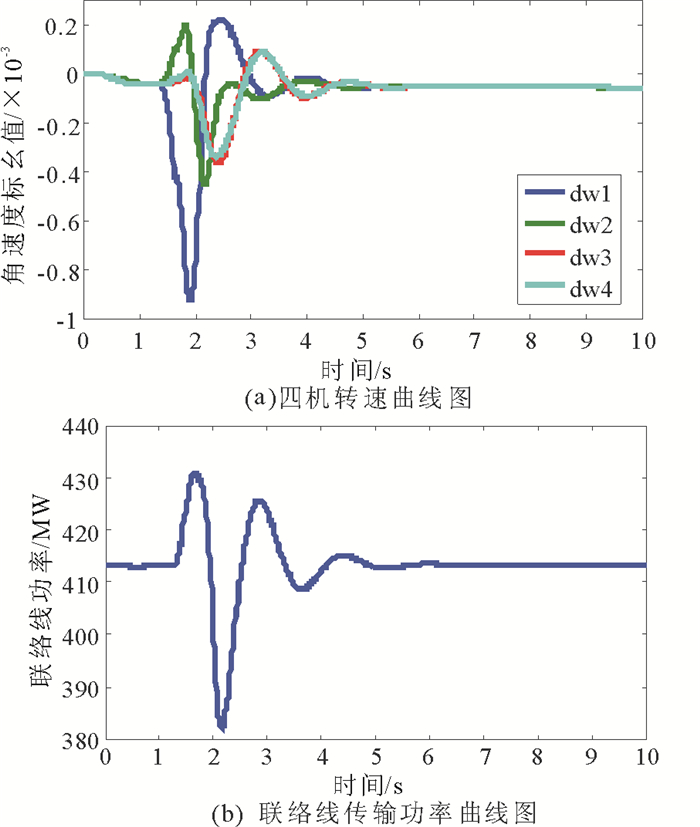
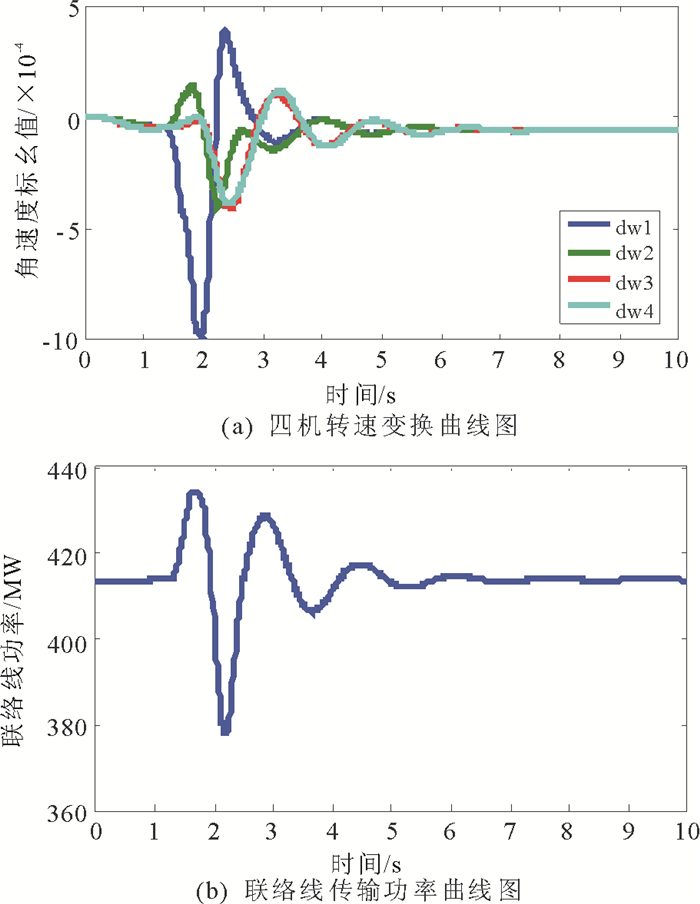
按表 3所给参数安装PSS后, 对发电机1的励磁参考电压施加相同的干扰, 此时受到干扰的系统状态变量经过两个周期左右的衰减达到了平衡。图 9(a)给出了4机转速变换曲线, 4机的转速振荡经过两个周期基本衰减到很弱。图 9(b)给出了联络线传输功率曲线, 经过6s振荡时间后基本恢复平稳状态。说明此方法设计的PSS参数合理, 可以达到较满意的低频振荡抑制效果。
|
图 9 加入文中方法设计的PSS后系统转速和功率曲线 Fig. 9 System speed and power curve with our method |
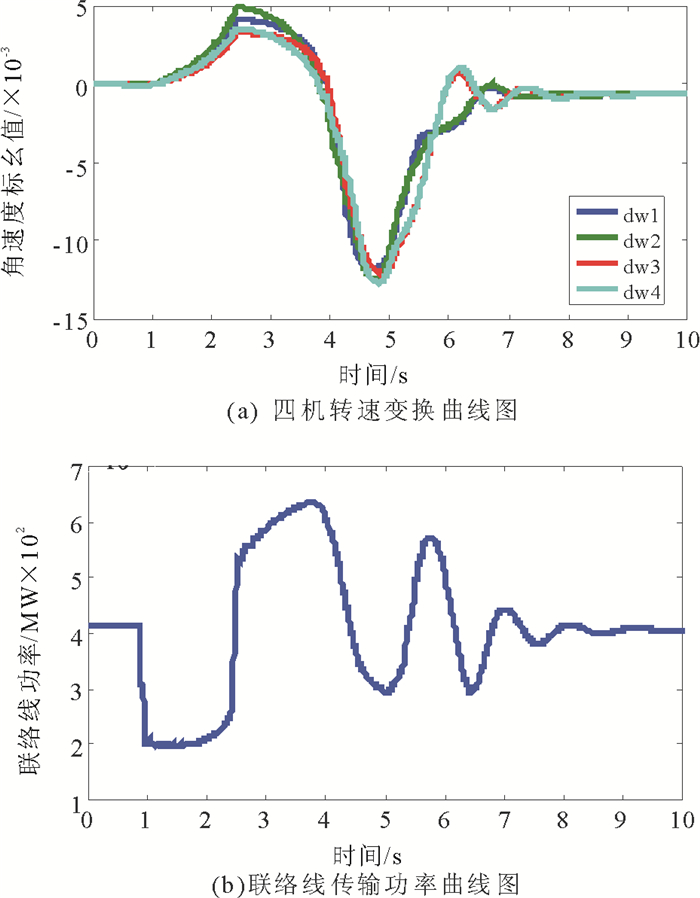
为试验PSS的适应性, 对4机2区域系统其中1联络线在1s时刻发生三相短路, 持续时间12/60s。此时受到干扰的系统状态变量经过两三个周期的衰减达到了平衡, 如图 10(a)给出了4机转速变换曲线和联络线传输功率曲线图 10(b)。这进一步说明, 此方法设计的PSS参数具有较好的适应性, 可以有效抑制机电振荡, 提高系统稳定运行水平。
|
图 10 三相短路故障下加入文中方法设计的PSS后系统转速和功率曲线 Fig. 10 System speed and power curve with our method under the three-phase short-circuit fault |
文中深入分析了以Heffron-Philips模型为基础的低频振荡的负阻尼机理, 推导了励磁系统滞后特性与各状态变量之间的联系, 讨论了PSS增益设计问题, 并在此基础上设计了PSS参数。相比于留数法, 其无需知道干扰信号和系统传递函数, 方便简单, 并通过实验仿真分析结果说明该方法设计的PSS能有效地抑制电力系统低频振荡。
| [1] |
陈恩泽, 刘涤尘, 廖清芬, 等. 多重扰动下的跨区电网低频振荡研究[J]. 电工技术学报, 2014, 29(2): 290-296. DOI:10.3969/j.issn.1000-6753.2014.02.035 |
| [2] |
宋墩文, 杨学涛, 丁巧林, 等. 大规模互联电网低频振荡分析与控制方法综述[J]. 电网技术, 2011, 35(10): 22-27. |
| [3] |
张晓明, 庞晓燕, 陈苑文, 等. 四川电网低频振荡及控制措施[J]. 中国电力, 2000, 33(6): 35-39. |
| [4] |
袁野, 程林, 孙元章, 等. 基于系统留数矩阵的广域PSS设计[J]. 电力系统自动化, 2007, 24: 1-6. |
| [5] |
霍承祥, 刘增煌, 朱方. 运用电力系统稳定器对励磁系统进行相位补偿的理论与实践[J]. 中国电机工程学报, 2015, 35(12): 2989-2997. |
| [6] |
范国英, 郭雷, 孙勇, 等. BFO-PSO混合算法的PSS参数优化设计[J]. 电力系统及其自动化学报, 2010, 22(6): 28-31. DOI:10.3969/j.issn.1003-8930.2010.06.006 |
| [7] |
闫健杰, 赵书强, 崔小磊. 基于改进遗传算法的多机系统PSS参数协调优化[J]. 华北电力大学学报, 2006, 33(2): 16-20. |
| [8] |
郭成, 李群湛. 基于改进PSO算法的SSSC广域阻尼控制器设计[J]. 电工技术学报, 2010, 25(1): 151-158. |
| [9] |
吴峰, 陈维荣, 李奇, 等. 基于粒子群优化算法的PSS参数优化[J]. 电力系统保护与控制, 2009, 37(10): 53-58. |
| [10] |
李春艳, 孙元章, 彭晓涛, 等. 采用广域测量信息反馈的广域PSS参数设计[J]. 电力系统自动化, 2009, 33(18): 6-11. |
| [11] |
杨晓静, 赵书强, 马燕峰. 采用广域测量信号的PSS参数优化设计[J]. 电力自动化设备, 2006, 26(3): 47-50. DOI:10.3969/j.issn.1006-6047.2006.03.014 |
| [12] |
陈刚, 程林, 孙元章, 等. 基于小信号激励的多机PSS参数在线闭环整定[J]. 电力系统自动化, 2011, 35(5): 5-9. |
| [13] |
赵璐. 电力系统稳定器在抑制系统低频振荡中的应用[J]. 上海电力学院学报, 2012, 28(5): 413-416. |
| [14] |
束洪春. 电力工程信号处理应用[M]. 北京: 科学出版社, 2011: 185-216.
|
| [15] |
孙勇.电力系统附加阻尼控制器的优化配置与设计方法研究[D].哈尔滨: 哈尔滨工业大学, 2009.
|
 2017, Vol. 47
2017, Vol. 47