2. 齐齐哈尔工程学院 建筑工程系, 黑龙江 齐齐哈尔 161000;
3. 空军装备部, 北京 100843
2. Department of Construction Engineering, Qiqihar Institute of Technology, Qiqihar 161000, China;
3. Air Force Armament Division, Beijing 100843, China
飞行性能模型预测主要包括航迹预测、姿态预测、时间预测、速度预测和油量预测等, 是研究飞行问题的前提和基础, 可以应用在多个领域[1-2]。比如:飞行性能模型是研究航线规划和航迹预测的基础, 只有快速准确地建立飞行性能模型, 才能够实现精准的预测和规划; 飞行性能模型组件也是飞机辅助决策系统的关键部分, 有效地建立敌方飞行性能模型, 对敌方意图进行预判, 可以为我方飞行员决策提供宝贵意见。因此, 研究飞行性能模型具有重要意义。
目前,对飞行性能模型的研究主要分为两类:一类是基于理论分析的参数方法, 通过对不同飞行阶段建立运动方程, 确定飞机的运动状态量。但是在求解模型时, 忽略了许多无法实时测量的参数, 像飞机所处位置的风速、温度和大气压力等, 同时也没有考虑管制因素, 使得模型的准确度降低[3-5];另一类是基于历史数据的经验方法, 通过分析历史数据, 将模型中的关键因子提取出来, 实现对飞行性能模型的逼近和预测, 交互式多模型滤波[6]、数据挖掘等算法[7-8]被广泛地应用于飞行性能模型的预测中。BP神经网络[7]由于以逼近任意非线性函数, 并且具有优秀的非线性映射和独有的多输入多输出功能, 因此经常被应用于飞行性能模型研究[6]。但是,BP神经网络是一种静态神经网络, 而飞行性能模型具有动态特性, 与前几个时刻的数据相关联, 使得基于BP神经网络的飞行性能模型的泛化能力上存在一定的局限性。
本文首先对BP神经网络算法进行改进, 引入动量因子和动态调整学习率, 并对输入数据进行适当处理, 改善了神经网络的不稳定性能和泛化能力。然后在BP神经网络的结构基础上提出了一种带外部输入的非线性自回归(nonlinear autoregressive network with exogenous inputs, NARX)神经网络[9], 加入了外部输入量的时间序列和输出量的反馈时延连接, 使得网络不仅具有动态特性,还能够借鉴历史数据信息, 克服了BP神经网络预测的不连续性和静态性, 极大地提高了飞行性能模型的预测精度。
1 飞机飞行性能模型关键要素分析飞机飞行性能是指飞机在做定常或非定常运动的过程中表现的基本飞行能力、机动飞行能力、巡航飞行能力以及起飞、着陆能力。飞行性能模型是一个复杂的非线性动态系统, 受到多种因素影响。其中, 飞行员的操纵量是影响飞机飞行性能的关键要素, 飞机性能指标和飞机飞行环境虽然也会对飞行性能模型产生一定的影响, 但由于数据无法获得, 不能进行实验分析, 本文只考虑飞行员的操纵量。
在飞机飞行过程中, 飞行员通过对操纵系统的控制, 保证对飞机纵向、横向、航向以及在机动飞行和起飞着陆时机翼増升装置的操纵, 改变飞机的运动状态。飞行员通过纵向操纵驾驶杆使升降舵发生偏转, 产生俯仰力矩, 飞机做俯仰运动; 通过横向操纵驾驶杆使襟副翼和左右平尾发生偏转, 产生滚转力矩, 飞机做滚转运动; 通过操纵脚蹬使方向舵发生偏转, 产生使飞机侧滑以及航向变化的偏航力矩, 飞机做偏航运动; 通过操纵油门杆改变飞机发动机的性能。
综上所述, 飞行员通过操纵飞机驾驶杆、油门杆和脚蹬, 改变飞机的运动状态, 极大地影响了飞机飞行性能。因此, 将飞行员的操纵量作为分析飞行性能模型的关键要素是合理的。
2 BP神经网络改进算法BP神经网络是一种由输入层、隐含层和输出层构成的多层前向静态神经网络, 其中输入层和输出层是单层, 隐含层可以根据实际问题进行调整, 使得BP神经网络的结构具有一定的灵活性。BP网络学习的主要特点是信号的顺序传播和误差的反向传播。在输入信号顺序传播的过程中, 输入信号输入到网络中, 经过输入层的线性处理进入隐含层, 然后经过隐含层的传播和处理, 最终到达输出层。
2.1 数据处理为了提高神经网络的收敛速度, 减少训练时间, 在数据输入到神经网络之前, 将训练数据和预测数据处理到0.5~1之间, 数据处理表达式为
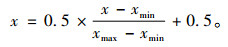
|
(1) |
式中, xmin表示变量x数据中的最小值, xmax表示变量x数据中的最大值。
2.2 引入动量因子在误差反向传播的过程中, 误差梯度下降法在处理复杂问题时很容易使BP网络停留在局部极值点上, 因此, 本文在权值和阈值调整公式中加入动量因子α:

|
(2) |
式中, n表示训练次数, h(n)表示第n次训练的梯度值, η表示学习率。如果动量因子很多, 即使网络陷入局部最小值也能够在一定时间里爬出来[10]。
2.3 自适应调整学习率由于在BP神经网络的训练过程中, 无法准确确定学习率的大小, 因此本文采取实时调整学习率的方法[11], 通过比较前后两次误差函数的数值改变学习率, 以提高神经网络的收敛速度。调节公式如下:
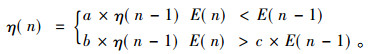
|
(3) |
式中, η(n)表示第n次训练的学习率, E(n)表示第n次训练的系统误差, a,b,c为常数, 取值范围分别为(1, 2),(0, 1)和[1, 1.1]。
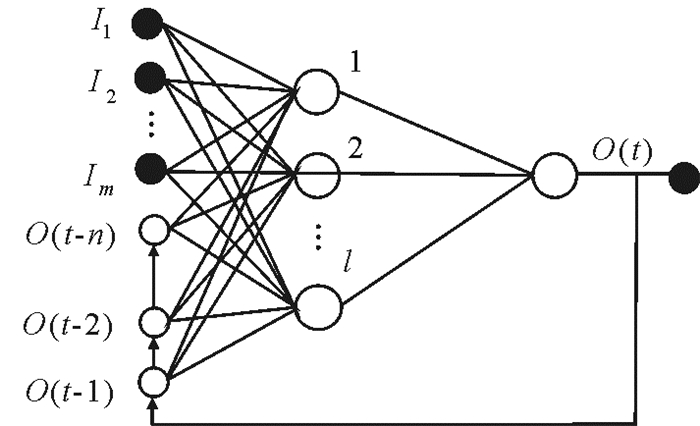
3 NARX神经网络预测模型 3.1 NARX神经网络原理NARX神经网络是一种动态神经网络, 与BP静态神经网络相比, 在结构上增加了从输出到输入的反馈连接, 包含外部输入量和输出量的时间序列, 具有更丰富的历史状态信息和优秀的动态特性, 能够很好地逼近非线性动力学模型[12]。NARX神经网络结构图如图 1。
|
图 1 NARX神经网络结构图 Fig. 1 The structure picture of NARX neural network |
在图 1中, NARX神经网络的输入层包含m个外部输入变量Ik和n个输出变量O(t)的反馈延迟输入变量O(t-i), 其k=1, 2, …, m, i=1, 2, …, n, 隐含层包含l个神经元节点。一般情况下, 输出层只包含一个输出变量。假设外部输入变量Ik的延迟长度为u, 输出变量O(t)的反馈延迟长度为n, t时刻的反馈延迟输入变量C(t)={O(t-1), …, O(t-n))}, NARX神经网络的数学表达式为
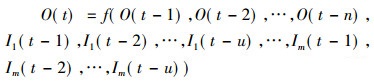
|
(4) |
第j个隐含层节点的输出为
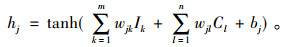
|
(5) |
NARX神经网络是在BP神经网络算法的基础上, 增加了神经网络输出量的反馈延迟输入, 并同时考虑了外部输入量对输出量的影响, 来提高模型的预测精度[13]。
3.2 训练算法由于NARX神经网络只是在结构上对BP神经网络进行改进, 内部权值和阈值调节的核心算法不变, 为了更好地将NARX神经网络和BP神经网络进行比较, 训练算法选取经典的收敛速度较快的LM算法[14]。而改进的BP神经网络采用动量法和自适应调整学习率算法, 提升网络的稳定性和灵活性[15]。
3.3 评价指标为了评价模型的预测精度和训练速度, 本文将神经网络的实际输出和目标输出产生的均方差mse和网络训练迭代次数作为模型评价指标:

|
(6) |
式中, N表示向后预测的步数, yi表示第i步预测的实际输出值, hi表示第i步预测的期望输出值, ei表示第i步预测的误差N。NARX预测模型的流程图如图 2。

|
图 2 预测模型流程图 Fig. 2 Flow chart of prediction model |
本文选取某一型号飞机, 通过飞行模拟器在特定仿真环境下飞行得到数据, 由于在飞行过程中几乎不使用脚蹬, 只选取驾驶杆横向和纵向的偏移量、油门杆的偏移量和时间作为神经网络的输入量, 以预测飞机航迹为例, 选取表示飞机位置的3个坐标作为神经网络的输出量。从一条航线数据中筛选出100组样本数据, 其中65组数据作为训练数据, 13组数据作为校验数据, 13组数据作为测试数据, 最后用训练好的神经网络模型对后9组数据进行预测, 评价模型的泛化能力。在利用NARX神经网络预测飞行性能模型时, 选取动态实时调整网络输入数据的方式, 利用上一时刻输出变量的实际值代替预测值, 预测下一时刻的输出变量。
4.2 参数设置本文同时采用BP神经网络、改进BP神经网络和NARX神经网络对飞行性能模型进行研究, 比较不同类型神经网络的预测结果。为了防止发生过拟合现象, 神经网络设计为3层, 训练精度设置为5×10-5, 隐含层节点数设计为20, 隐含层传递函数设计为双曲正切Sigmoid函数, 输出层传递函数设计为线性函数。根据经验, 设置学习率为0.1, 动量因子为0.08, 为了保证足够收敛, 最大训练次数设计为10 000次, NARX神经网络输入量和输出量的时间延迟均设置为2。
4.3 仿真结果及分析分别利用BP神经网络、改进BP神经网络和NARX神经网络训练前91组飞行数据, 实验结果表明,3种神经网络都达到了预定的精度, 使用得到的神经网络模型对后9组数据进行预测, 预测结果仿真曲线如图 3~5。

|
图 3 X坐标预测结果仿真曲线 Fig. 3 Result of simulation curve for X-coordinate forecasting |

|
图 4 Y坐标预测结果仿真曲线 Fig. 4 Result of simulation curve for Y-coordinate forecasting |

|
图 5 Z坐标预测结果仿真曲线 Fig. 5 Result of simulation curve forZ-coordinate forecasting |
从图 3、图 4、图 5中可以看出, 飞机位置坐标的预测结果准确度大小依次是NARX神经网络>改进BP神经网络>BP神经网络, 3种方法预测的趋势和实际趋势大致相同, 但BP神经网络的预测值与实际值相差较大, 改进的BP神经网络虽然在一定程度上提高了预测精度, 但是随着时间的积累, 误差逐渐增大, 只有NARX神经网络准确地预测了飞机的位置, 并且预测结果不会受到时间的影响。
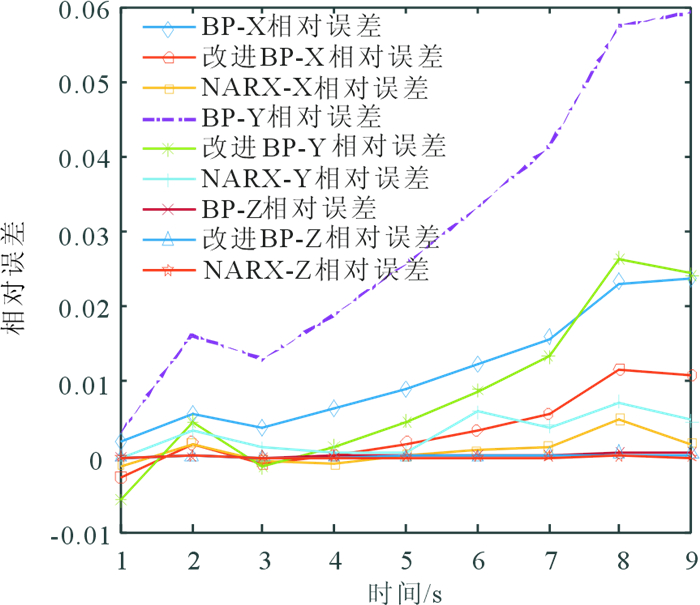
从图 6中可以看出, NARX神经网络预测结果的相对误差始终比较稳定, 不会出现某一次过大的现象, 预测效果较好, 而BP神经网络和改进的BP神经网络相对误差曲线波动较大, 并且处于上升的趋势, 不能持续地预测飞机位置。
|
图 6 飞机位置预测结果相对误差曲线 Fig. 6 Result ofrelative error for flight location forecasting |
从图 7可以看出, 只有NARX神经网络准确地预测了飞机的位置, 每一个位置的预测点与实际点相差较小, 有的甚至和实际位置重合, 而其他两种神经网络预测的位置和实际位置偏差较大, 并且预测的位置和上一个位置不连续, 不具有实际应用价值。

|
图 7 飞机位置预测曲线图 Fig. 7 Forecast curve of flight location |
表 1和表 2给出了3种神经网络训练的迭代次数和预测飞机位置的3个坐标均方误差。
|
|
表 1 神经网络迭代次数表 Tab. 1 Number of iteration for neural network |
|
|
表 2 神经网络均方误差表 Tab. 2 Mean square error of neural network |
从表 1可以看出, 基于LM算法的BP神经网络和NARX神经网络收敛速度较快, 而基于动量法和自适应调节学习率算法的改进,BP神经网络由于实时调整学习率和网络权值, 收敛速度慢, 迭代次数比其他两种神经网络多, 从表 2可以看出, NARX神经网络预测精度很高, 3个坐标预测的均方误差比其他两种神经网络小得多, 具有实际应用价值。
5 结论本文使用3种神经网络根据飞行员的操纵量和时间预测飞机的位置等状态量的变化。由于飞行性能模型是一个复杂的非线性动态系统, 而BP神经网络和改进的BP神经网络是一种静态神经网络, 忽略了输入量和输出量的历史状态信息, 无法准确地逼近动态系统, 预测结果较差, 并且不具有持续预测的能力。NARX神经网络在BP神经网络结构的基础上加入了输入量和输出量的时间序列, 使得神经网络具有动态特性和保留更多的历史状态信息, 准确地预测了飞机的位置, 基于LM算法NARX神经网络的收敛速度较快。在利用NARX神经网络预测时, 使用单步向前预测, 并且根据实际飞行数据实时更新预测数据, 使得模型在长期预测时始终保持较高的预测精度。NARX神经网络预测方法为航线规划、航迹预测和民航交通系统等提供了一种新的基于数据的神经网络建模思路和方法, 可以既保证预测精度又保证收敛速度, 克服了基于数据方法的输入信息少、模型不准确等缺点, 具有重要意义。
| [1] |
陈廷楠. 飞机飞行性能品质与控制[M]. 北京: 国防工业出版社, 2007.
|
| [2] |
马东立, 包文卓, 乔宇航. 基于重力储能的太阳能飞机飞行轨迹研究[J]. 航空学报, 2014, 35(2): 408-416. |
| [3] |
王超, 郭九霞, 沈志鹏. 基于飞行模型的4D航迹预测方法[J]. 西南交通大学学报, 2009, 44(2): 295-300. DOI:10.3969/j.issn.0258-2724.2009.02.028 |
| [4] |
汤新民, 韩云祥, 韩松臣. 基于混杂系统模型的航空器4D航迹推测[J]. 南京航空航天大学学报, 2012, 44(1): 105-112. DOI:10.3969/j.issn.1005-2615.2012.01.019 |
| [5] |
THIPPHAVONG D P, SCHULTZ C A, LEE A G, et al. Adaptive algorithm to improve trajectory prediction accuracy of climbing aircraft[J]. Journal of Guidance, Control and Dynamics, 2013, 36(1): 15-24. DOI:10.2514/1.58508 |
| [6] |
王涛波, 黄宝军. 基于改进卡尔曼滤波的四维飞行航迹预测模型[J]. 计算机应用, 2014, 34(6): 1812-1815. DOI:10.3969/j.issn.1001-3695.2014.06.050 |
| [7] |
谭伟, 陆百川, 黄美灵. 神经网络结合遗传算法用于航迹预测[J]. 重庆交通大学学报(自然科学版), 2010, 38(1): 147-150. |
| [8] |
王俭臣, 齐晓慧. 基于EPSO-BP的Elman网络及其在飞行轨迹预测中的应用[J]. 控制与决策, 2013, 28(12): 1884-1888. |
| [9] |
CAI L, MA S Y, CAI H T, et al. Prediction of SYM-H index by NARX neural network from IMF and solar wind data[J]. Sci China Ser E-Tech Sci, 2009, 52(10): 2877-2885. DOI:10.1007/s11431-009-0296-9 |
| [10] |
RUMELHARD D E, HINTON G E, WILLIANMS R J. Learning representations by back-propagation errors[J]. Nature, 1986, 323: 533-536. DOI:10.1038/323533a0 |
| [11] |
李伟, 何鹏举, 杨恒, 等. 基于粗糙集和改进遗传算法优化BP神经网络的算法研究[J]. 西北工业大学学报, 2012, 30(10): 601-606. |
| [12] |
吴建锋, 何小荣, 陈丙珍. 动态过程神经网络模型的研究(一)[J]. 系统工程理论与实践, 2001, 21(12): 47-53. DOI:10.3321/j.issn:1000-6788.2001.12.009 |
| [13] |
刘天舒. BP神经网络的改进研究及应用[D].哈尔滨: 东北农业大学, 2011.
|
| [14] |
魏津瑜, 张玮, 李欣. 基于PSO-BP神经网络的高炉煤气柜位预测模型及应用[J]. 中南大学学报, 2013, 44(增刊): 266-270. |
| [15] |
SINGHAL D, SWARUP K S. Electricity price forecasting using artificial neural networks[J]. Electrical Power and Energy Systems, 2011, 33(3): 550-555. DOI:10.1016/j.ijepes.2010.12.009 |
 2017, Vol. 47
2017, Vol. 47

