智能交通系统(ITS)是将先进的信息技术、传感技术、控制技术和计算机技术等有效地集成运用于整个交通运输管理体系, 从而建立起一种全方位、实时、准确及高效的综合运输系统[1-2]。智能车辆是智能交通系统领域最重要的组成部分[3], 无人驾驶是实现智能汽车与智能交通的关键技术, 也是未来汽车的发展方向与必然趋势[4]。
轨迹规划作为无人驾驶汽车技术领域的研究重点之一, 其任务是在位姿空间中找到一条从初始位姿点到目标位姿点的连续无碰撞路径, 同时满足环境约束、时间约束以及动力学约束等条件[5], 与车辆的可靠性、安全性与乘坐舒适性密切相关。
常用的轨迹规划算法有图搜索算法、仿生智能算法、数值规划算法与基于采样算法等。目前, 已有不少文献对此展开研究。文献[6]与文献[7]分别针对A*图搜索算法与D*图搜索算法进行研究, 但是其计算时间和转角不满足汽车行驶要求。文献[8]采用卷积人工神经网络, 输入为障碍物信息, 输出为参考路径, 但人工神经网络训练较为困难。文献[9]与文献[10]分别采用了遗传算法与启发式蚁群优化算法, 然而存在算法收敛速度不稳定的缺点。文献[11]采用数值规划法, 最小化具有不同限制变量的目标函数, 实时性差, 计算时间长。快速搜索随机树法(RRT)是典型的基于采样的算法[12]。该算法通过在搜索空间均匀采样来扩展搜索区域, 逐步增加搜索路径, 最终到达目标区域[13], 能有效解决机器人在复杂环境下的轨迹规划问题。
然而RRT算法依赖于随机点选择, 运算较慢。文献[14-15]采用双向RRT算法, 对起始点和目标点同时发展生成树, 提高了轨迹扩展速度;文献[16]以一定的概率使目标点作为随机点, 增大树节点发展的偏向性, 提高运算速度, 然而上述两种算法在提高生成轨迹质量方面效果一般;文献[17-18]提出启发式代价RRT算法, 将环境代价作为算法的约束条件, 得到代价最小的路径,但启发式代价函数可用度量距离与真实距离不一致, 同时代价计算量巨大, 运算速度较慢;文献[19]结合图形搜索和随机树算法, 取得良好的控制效果; 文献[20-21]基于目标偏向与人工势场, 改进RRT算法在机器人上的应用; 文献[22]研究了地图中的轨迹生成算法, 用蒙特卡洛求碰撞概率, 同时采用B样条曲线对轨迹进行优化。以上研究对原始RRT算法提出较大的改进, 但研究对象为移动式机器人, 难以直接运用于车辆轨迹规划中。
因此, 本文根据无人驾驶汽车特性, 针对无人驾驶汽车轨迹规划问题, 考虑车辆运动学约束, 同时保证车辆稳定性与乘坐舒适性, 提出一种改进的RRT算法。首先,基于车辆模型与约束条件, 在扩展区域随机生成可达节点, 实现对随机点采样的区域控制; 其次,根据目标偏向原理, 以一定的概率把目标点作为随机点进行随机树扩张, 提高路径的生成速度, 并采用三次B样条曲线进行轨迹平滑处理;最后,基于Matlab/CarSim联合仿真平台, 仿真分析了本文提出的轨迹规划算法的优劣。
1 车辆转向约束模型在无人驾驶车辆轨迹规划过程中需考虑车辆运动学约束, 以得到满足车辆转向机构运动特性的行驶路径。
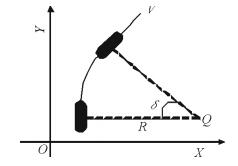
由于转向系统对车辆的垂向运动影响甚微, 因此, 将无人驾驶汽车的运动视为平行于水平面的平动, 将前后轮分别用一个等效前轮和一个等效后轮来代替。同时,考虑到模型的控制变量是车辆的转向角, 主要涉及车辆的侧向动力学, 假定车辆速度恒定, 忽略车辆的纵向动力学, 建立车辆转向模型, 如图 1所示。
|
图 1 车辆转向模型 Fig. 1 Vehicle steering model |
由此可得
| $ \delta = {\rm{arctan}}\frac{L}{R} 。$ | (1) |
其中, δ为前轮转角; L为轴距; R为路径半径。
考虑车辆转向系机械结构约束, 跟踪所规划路径时前轮转角需小于车辆的最大转角δmax,即
| $ \left| \delta \right| < {\delta _{\max }} 。$ | (2) |
RRT算法是一种基于概率采样的增量式搜索算法, 搜索所需边界点少, 搜索范围趋向于未知区域, 可达性好, 具有概率完整性, 不需要对空间建模, 能快速搜索复杂高维空间, 适用于非完整与高自由度状态下的轨迹规划, 在智能寻迹领域应用广泛。
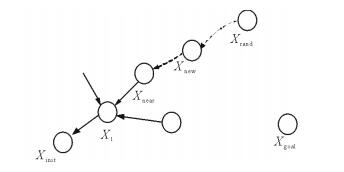
RRT算法在满足条件的搜索区域内进行搜索, 定义整体状态空间X与自由空间Xfree∈X, 使得起始点Xinit∈X, 目标点Xgoal∈X, 障碍物Xobs∈X。随机树最终生成在自由空间Xfree中, 其中Xinit∈Xfree, Xgoal∈Xfree。以起始点为根节点, 定义控制量空间U及时变输入控制量u(t)∈U, t∈[0, T], 得状态转换方程
|
图 2 随机树扩展方式图 Fig. 2 Expansion of random tree |
在搜索过程中, 选择Xinit作为随机树起始点Tr.int, 设定算法迭代步数为k。通过RANDOM_STATE在整体状态空间X中生成单个状态位置随机点Xrand, 若与障碍物冲突, 则重新生成随机点。利用NEAREST_NEIGHBOR(Xrand, T)在随机树上寻找与随机点最近的树节点Xnear。依据两点间位置关系, 利用NEW_STATE(ε, Δt)沿该树节点到随机点Xrand扩展一个步长ε,并产生新的树节点Xnew。算法持续迭代, 通过不断增加子树节点Tree.add, 延伸扩展产生随机树NewTree, 直到目标节点Xgoal成为树节点或距离树节点不足一个步长, 完成搜索, 实现随机树的构造。此时从目标点起, 回溯全树, 则可获得一条从起始位置到目标位置的可行路径。
3 基于改进型RRT算法的轨迹规划研究 3.1 基于RRT算法的轨迹规划需求分析由于原始RRT算法的可行区域为整体环境区域, 以可达性为首要要求, 采样随机性高, 适合于扩展未知区域, 方向变化较大, 运动约束性差, 生成的路径适用于可随时进行全方位转向的移动式机器人的运动。而车辆运动约束较高, 行进方式一般为区域性向前行驶, 不会产生较大幅度的转向、频繁且长时间后退等行驶行为, 原始RRT算法与汽车的运动符合度低,同时, 原始RRT算法随机点产生范围为整个可行区域, 算法偏向性小, 产生较多无效节点, 路径生成较慢。
因此, 基于建立的车辆运动约束模型, 本文对轨迹规划提出的具体要求如下:
1) 前轮转角满足机械转向结构的约束;
2) 在随机点生成阶段剔除无效节点, 提高搜索效率, 满足轨迹规划的实时性要求;
3) 车辆行驶过程中, 将转角保持在较低值, 且减小转角变化率, 保证车辆行驶的稳定性和乘坐的舒适性;
4) 尽可能使路径平直化, 使前轮转角在可控范围内, 减少转向行为;
5) 对生成轨迹做平滑处理, 降低跟踪轨迹时的侧向加速度。
3.2 改进RRT算法设计为满足上述车辆轨迹规划的要求, 提出改进的RRT算法。在RRT算法的采样过程中进行采样区域限制, 根据车轮可达转角, 将随机点的采样限制在前进方向的可行域内, 可行域以车辆纵轴线为中间线, 分别向左右转动到车轮极限转角位置, 从而产生一个向前的采样范围。同时,该区域能避免无效区随机点的产生, 提高规划速度和轨迹生成质量。
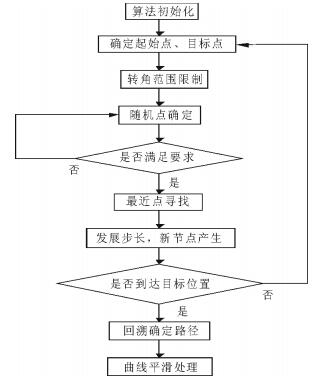
基于改进的RRT算法确定采样区域、起始点与目标点, 在可行域内产生随机点, 并对随机点进行碰撞检测, 将不发生碰撞的随机点加入可达集, 连接曲率变化最小的点, 生成初始轨迹, 最后对轨迹进行平滑处理与优化。具体算法流程图如图 3所示。
|
图 3 改进RRT算法流程图 Fig. 3 Flow chart of improved RRT algorithm |
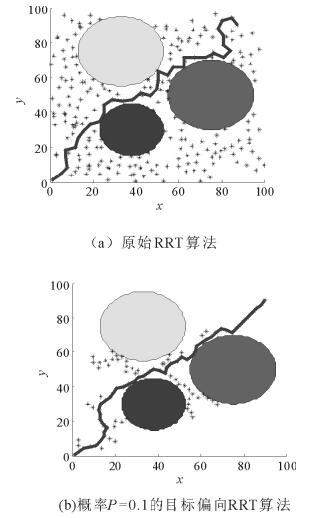
原始RRT算法的随机点为可行区域内任意一点, 随机点选择范围大, 随机树的发展缺乏一定的导向性, 导致算法在寻找目标点时将产生不必要的工作, 耗时较长。因此, 基于目标偏向原理, 在进行随机点选择时, 以概率P将目标点作为随机点进行随机树扩张, 以增加随机树向目标点的扩展概率, 从而有效降低采样点的数量, 加快随机树的生成[18], 提高轨迹规划速度,同时,轨迹也更为平滑, 有利于提高行驶稳定性。RRT算法与目标偏向RRT算法曲线生成对比如图 4所示。由图 4可知, 基于目标偏向的RRT算法采样点显著减少, 可大大缩短轨迹规划所用的时间, 生成路径也较为平整光滑, 满足车辆轨迹的一般要求。
|
图 4 目标偏向对比图 Fig. 4 Chart of target bias comparison |
考虑到车辆的行驶稳定性与乘坐舒适性, 基于上述车辆约束条件, 设定车辆最大航向角为40°, 左右轮转角相等, 考虑采样点范围, 设计随机点可达区, 扩展的随机点需位于规定范围内, 且随机点与树节点距离需大于一个步长, 继而确定可优先被扩展的点。
随机点产生在车辆转角扇形范围内, 如图 5所示, 当车辆位于Xnear节点沿X轴正向行驶时, 转角边界为粗实线。随机点与最近树节点的连线与最近树节点与父节点的连线夹角小于最大航向角, 生成的随机点有效。
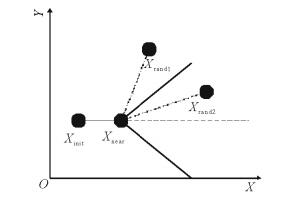
|
图 5 随机点产生限制范围 Fig. 5 Limited range of random points |
随机点坐标为(x, y), 最近树节点坐标为(x(t1), y(t1)), 父节点坐标为(x(t0), y(t0)), 最近树节点与父节点连线及最近树节点与随机点连线的斜率可分别表示为
| $ {k_1} = \frac{{y\left( {{t_1}} \right) - y\left( {{t_0}} \right)}}{{x\left( {{t_1}} \right) - x\left( {{t_0}} \right)}}, $ | (3) |
| $ {k_2} = \frac{{y - y\left( {{t_1}} \right)}}{{x - x\left( {{t_1}} \right)}} 。$ | (4) |
其中, k1为最近树节点与父节点连线的斜率, k2为最近树节点与随机点连线的斜率。
两直线夹角β为
| $ \beta = {\rm{arctan}}\left( {\frac{{{k_1} - {k_2}}}{{1 + {k_1} \cdot {k_2}}}} \right) 。$ | (5) |
可扩展区的转角约束条件为
| $ \beta < {\delta _{\max }} 。$ | (6) |
RRT算法的最近点Xnearest的获取采用欧氏距离进行计量, 即以直线距离的长度来寻找与随机点最近的树节点, 从而产生路径。虽然路径在车辆转向系约束的可达范围内, 但可能导致较大的方向盘转角。因此, 考虑车辆运行的稳定性与乘坐舒适性, 转角小的随机点将优先被扩展。
3.4 轨迹平滑处理算法设计上述算法生成的轨迹是由短线段连接而成的不平滑轨迹, 为了进一步提高规划轨迹的平滑度和汽车的跟踪稳定性, 需对原始轨迹进行平滑处理。轨迹平滑处理常用的曲线为抛物样条曲线和参数样条曲线, 然而这两种方法生成的曲线通过所有给定的点, 某些点的存在可能会对曲线平滑度造成不利影响。贝塞尔曲线具有连续性和局部性, 因此, 本文选择基于贝塞尔曲线的B样条曲线进行轨迹平滑处理。分别采用二次B样条曲线与三次B样条曲线对特定控制曲线进行拟合, 拟合结果如图 6所示。由图 6可知, 经B样条曲线拟合后, 所得曲线能够沿给定趋势变化, 剔除了控制曲线中的尖点及曲率半径较小处的点, 曲线的平滑度有了一定程度的提高。其中, 三次B样条拟合曲线的曲率半径更小, 尖点处的过渡更为平滑, 适用于车辆规划轨迹, 因此, 本文选取三次B样条曲线进行轨迹平滑处理。
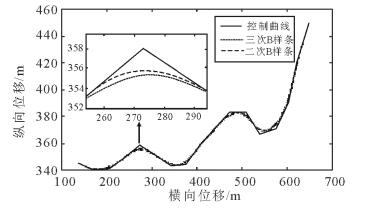
|
图 6 B样条曲线拟合 Fig. 6 B spline curve fitting |
B样条曲线方程可表示为
| $ p\left( u \right) = \sum\limits_{i = 0}^n {{d_i}{N_{i,k}}\left( u \right)} 。$ | (7) |
其中,
三次B样条曲线的基函数为
| $ {b_0} = 1/{6^*}\left( { - {u^3} + {3^*}{u^2} - {3^*}u + 1} \right), $ |
| $ {b_1} = 1/{6^*}\left( {{3^*}{u^3} - {6^*}{u^2} + 4} \right), $ |
| $ {b_2} = 1/{6^*}\left( { - {3^*}{u^3} + {3^*}{u^2} + {3^*}u + 1} \right), $ |
| $ {b_3} = 1/{6^*}{u^3} 。$ | (8) |
B样条拟合曲线为
| $ \begin{array}{l} \;\;\;\;\;\;\;x = b_0^*a\left( {1,i} \right) + b_1^*a\left( {1,i + 1} \right) + b_2^*a\left( {1,} \right.\\ \left. {i + 2} \right) + b_3^*a\left( {1,i + 3} \right), \end{array} $ |
| $ \begin{array}{l} \;\;\;\;\;\;\;y = b_0^*a\left( {2,i} \right) + b_1^*a\left( {2,i + 1} \right) + b_2^*a\left( {2,} \right.\\ \left. {i + 2} \right) + b_3^*a\left( {2,i + 3} \right) 。\end{array} $ | (9) |
为全面、有效地模拟车辆运行环境, 本文基于Matlab/CarSim联合仿真平台, 对车辆在直线路况和直角路况下进行轨迹规划的仿真与分析。
直线路段由双向6车道构成, 取单向3车道, 车辆由中间车道换道至第3车道。单向车道总宽11.25m, 建立直线路况场景。
直角路段由双向4车道构成, 取单向双车道, 车辆右转90°行驶, 单向车道总宽7.5m, 建立直角路况场景。
4.2 仿真结果及分析为了验证本文提出基于车辆约束的改进RRT算法的优劣, 使用不同转角约束下的改进RRT算法与原始RRT算法在上述场景中进行仿真对比。将车辆尺寸等效至障碍物边界设计中, 车辆可看做质点, 取步长为15, 目标偏向概率为0.1。由于RRT算法是基于满足约束条件的随机点生成过程, 因此进行了多次仿真模拟。在上述场景路况中的规划轨迹分别如图 7与图 8所示, 红线为所得规划轨迹。
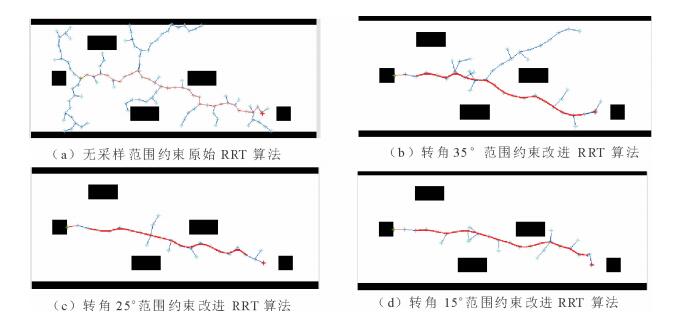
|
图 7 直线路况仿真结果 Fig. 7 Simulation results of straight road |
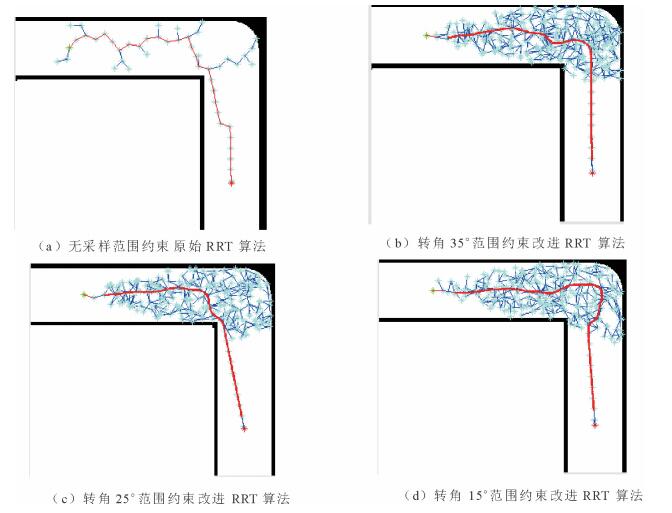
|
图 8 直角路况仿真结果 Fig. 8 Simulation results of right angle section |
由图 7(a)与图 8(a)可知, 在不同路况下, 原始RRT算法产生的树节点随机性强, 路径扩展偏向性较低, 生成路径中存在一定程度的折线与尖点, 同时,路径横向波动大, 车辆跟踪该轨迹时横向位移也大, 在尖点处车辆极有可能出现无法满足运动学约束而难以跟踪规划轨迹的现象。对于直线路况, 转角约束越大, 生成轨迹的平滑度越高。然而, 由图 8可知, 直角路况下在转角35°约束与25°约束时路径较为平滑, 而转角15°约束下弯道转折点处的轨迹反而产生了较大波动。
不同约束下所规划轨迹的曲率均值、曲率极大值与曲率方差如表 1所示。
|
|
表 1 轨迹曲率指标对比 Tab. 1 Comparison of curvature index for trajectory |
由表 1可知,两种路况下, 无约束RRT算法的曲率均值、极大值与方差较大, 加入转角约束后曲率均值、极大值与方差呈下降趋势。相比于无约束控制, 15°转角约束下直线路况规划轨迹的曲率均值、极大值与方差分别降低了22.9%,51.7%与43.3%, 表明随着约束的增加, 路径更为平滑; 直角路况下, 在一定的转角约束范围内, 随着约束的加强, 曲率均值也逐渐降低, 由无约束下的0.095 m-1降低到0.005 2m-1,然而,随着转角约束由25°加强到15°时, 曲率均值开始增大至0.006 7 m-1。
两种路况下的平均采样点数、平均树节点数与仿真平均时长如表 2所示。由表 2可知, 无约束RRT算法的平均采样点数、平均树节点数与规划所用时长明显高于有转角约束的RRT算法, 且随着约束的加强, 平均采样点数与规划所用时长均减小,平均树节点数比无转角约束条件下明显减小。相比于无转角约束, 15°转角约束下直线路况的平均采样点数、平均树节点数与规划所用时长分别降低了62.9%,38.2%与78.5%, 直角路况分别降低了34.0%,41.9%与27.4%, 直线路况下, 平均采样点数和算法完成时间下降程度更为显著。
|
|
表 2 轨迹生成实时性指标对比 Tab. 2 Comparison of real-time index for trajectory |
综上所述, 基于本文提出的改进RRT算法生成轨迹的平均曲率降低, 路径平滑度增加; 同时,由于平均采样点数与平均树节点数减少, 轨迹生成速率有了较大幅度的提高, 从而提高轨迹规划的实时性, 且能够适应较宽的车速范围, 在一定程度上满足车辆在高速行驶时的轨迹规划要求。改进RRT算法中约束选择对生成轨迹有较大影响, 直线路况时, 随着约束的增加, 轨迹平均曲率降低, 路径更为平滑; 然而在直角路况下, 过大的约束反而会导致较大的曲率, 应合理选择约束转角。
5 结语1) 本文以无人驾驶汽车为研究对象, 提出了一种基于车辆运动学约束与行驶稳定性的改进RRT轨迹规划算法, 并在不同路况下仿真分析了所提出算法的优劣。
2) 本文提出的改进RRT算法, 基于车辆的转向特性, 控制随机点的扩展区域, 同时,基于目标偏向策略以一定概率将目标点作为随机点进行随机树扩张, 最后采用三次B样条曲线平滑生成的轨迹, 在无人驾驶汽车轨迹规划中具有较强的实用性。
3) 本文提出的改进RRT算法采用仿真进行验证, 在直线路况及直角路况中均能规划出合理轨迹, 满足无人驾驶汽车对轨迹规划可达性、稳定性与实时性的要求, 将机器人运动轨迹研究中较为流行的RRT搜索算法运用于车辆轨迹规划领域。
4) 本文提出的改进RRT算法未考虑车速变化对规划轨迹的影响, 因此, 未来对转角约束与车速的关系进行系统研究, 对最大限度地保证稳定性与道路通行能力具有重要意义。
| [1] |
严新平, 吴超仲. 智能运输系统——原理、方法及应用[M]. 2版. 武汉: 武汉理工大学出版社, 2014.
|
| [2] |
金茂菁. 我国智能交通系统技术发展现状及展望[J]. 交通信息与安全, 2012, 30(5): 1-5. DOI:10.3963/j.issn.1674-4861.2012.05.001 |
| [3] |
《中国公路学报》编辑部. 中国交通工程学术研究综述·2016[J]. 中国公路学报, 2016, 29(6): 52. |
| [4] |
孟海华, 江洪波, 汤天波. 全球自动驾驶发展现状与趋势(上)[J]. 华东科技, 2014(9): 66-68. DOI:10.3969/j.issn.1006-8465.2014.09.015 |
| [5] |
LAVALLE S. Planning Algorithms[M]. New Yrok: Cambridge University Press, 2006.
|
| [6] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for theheuristic determination of minimum cost paths[J]. Acm Sigart Bulletin, 2007, 4(2): 100-107. |
| [7] |
DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269-271. DOI:10.1007/BF01386390 |
| [8] |
LU Y, YI S. A novel path planning method for biominmetic robot based on deep learning[J]. Assembly Automation, 2016, 36(2): 186-191. DOI:10.1108/AA-11-2015-108 |
| [9] |
FU S Y, HAN L W, TIAN Y, et al.Path planning for unmanned aerial vehicle based on genetic algorithm[C]//2012 IEEE Ⅱth International Conference on Cognitive Infoematics & Cognitive Computing(ICCI*CC).IEEE, 2012: 140-144.
|
| [10] |
GARCIA M A P, MONTIEL O, CASTILLO O, et al. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation[J]. Applied Soft Computing, 2009, 9(3): 1102-1110. DOI:10.1016/j.asoc.2009.02.014 |
| [11] |
冯来春, 梁华为, 杜明博, 等. 基于A~*引导域的RRT智能车辆路径规划算法[J]. 计算机系统应用, 2017, 26(8): 127-133. |
| [12] |
余卓平, 李奕姗, 熊璐. 无人驾驶车辆运动规划算法综述[J]. 同济大学学报(自然科学版), 2017, 45(8): 1150-1159. DOI:10.11908/j.issn.0253-374x.2017.08.008 |
| [13] |
胡兵, 何凤红, 毛剑琳. 基于改进RRT算法的AGV路径规划研究[J]. 软件导刊, 2018(3): 28-31. |
| [14] |
杜爽, 尚伟伟, 刘坤, 等. 基于双向RRT算法的仿人机器人抓取操作[J]. 中国科学技术大学学报, 2016, 46(1): 12-20. |
| [15] |
KUFFNER J, LAVALLE S M. RRT-connect: An efficient approach to single-query path planning[C]//Proceedings of the IEEE International Conference on Robotics and Automation (ICRA). San Francisco: IEEE, 2000: 995-1001.
|
| [16] |
乔慧芬.机器人路径规划算法研究[D].广州: 中山大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10110-1015583211.htm
|
| [17] |
CHENG P, LAVALLE S M. Resolution complete rapidly-exploring random trees[C]//IEEE International Conference on Robotics and Automation(ICRA). IEEE, 2002: 267-272.
|
| [18] |
URMSON C, SIMMONS R. Approaches for heuristically biasing RRT growth[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2003: 1178-1183.
|
| [19] |
GAMMELL J D, SRINIVASA S S, BARFOOT T D. Batch Informed Trees (BIT*): Sampling-based optimal planning via the heuristically guided search of implicit random geometric graphs[C]//IEEE International Conference on Robotics and Automation. IEEE, 2015: 3067-3074.
|
| [20] |
李威洲.基于RRT的复杂环境下机器人路径规划[D].哈尔滨: 哈尔滨工程大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10217-1013171942.htm
|
| [21] |
郝利波.基于改进RRT与人工势场混合算法的足球机器人路径规划研究[D].西安: 西安科技大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10704-1011300187.htm
|
| [22] |
江庆坤.智能汽车避障危险评估和轨迹规划研究[D].长春: 吉林大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016079601.htm
|
 2018, Vol. 48
2018, Vol. 48