自从2008年金融危机以来, 国际形势动荡不安, 英国脱欧等黑天鹅事件频发, 而我国作为全球化浪潮中的重要力量, 如何应对纷繁复杂的证券金融形势是我国政府及民众关注的热点之一。近年来随着开放式基金的飞速发展, 日益成为我国证券投资领域一股不可忽视的力量, 如何科学有效地对其进行绩效评价, 成为学者们的研究热点。
1 绪论回顾以往的文献, 国外的相关研究远远领先于我国。自1952年Markowitz提出投资组合理论, 奠定了证券市场的理论基础[1]。Treynor指数[2]、Sharpe指数[3]、Jensen指数[4]以及CAPM模型[5]的提出, 对金融领域产生了深远的影响。其后, 证券投资领域的研究由单因素静态向多因素动态模型发展。1992年Fama与French针对美国股票市场提出了著名的Fama-French三因子模型[6], 利用市场风险溢价因子、市值因子与账面市值比因子解释股票收益的变动情况。在此基础之上, Carhart(1997)加入动量因素, 构成Carhart四因素模型[7]。在随后的实际应用中, 上述模型由于本身解释能力的限制, 均受到了不同程度的挑战。而在2015年Fama与French再一次提出五因子模型, 该模型是对三因子模型的拓展与延伸, 引入盈利能力因子与投资水平因子, 是对三因子模型的改进与补充, 且该模型在美国证券市场得到了验证[8]。相较于国外, 国内学者大部分是运用已有的经典模型进行实证检验, 从以往的封闭式基金逐渐转向开放式基金。屠新曙、朱梦(2010)[9]选取30只开放式基金, 运用三因子模型进行绩效评价, 研究表明, 我国开放式基金具有获得超额收益的能力。我国学者大多借用三因子模型对基金的投资风格进行研究。许永峰等(2015)[10]运用层次分析与模糊数学的方法对样本基金进行了绩效评价。齐岳、孙信明(2016)[11]选取华夏成长、南方绩优、博时新兴与博时精选四只分别代表增长型、收益型与平衡型的开放式基金进行分析, 首次以构建股票投资策略的模式, 对基金绩效进行动态评价。结果表明, 基金宣称的投资策略并没有在实际运作中得以坚持, 且样本基金的选股择时能力较差。随着五因子模型的提出, 国内学者也逐步展开相应的研究。赵胜民等(2016)[12]以我国1995年1月至2014年12月沪深两市A股的截面数据作为样本, 对比研究三因子与五因子模型在我国的适用性问题。宋光辉等(2017)[13]在Fama-French五因子模型的基础上, 引入流动性作为风险因子, 形成六因子模型, 对我国股票市场的动量效应进行了有力的解释。本文基于多因子模型, 重新构建了基金投资组合中的十大重仓股, 从而建立了基于多因子的差值模型, 进而对股票型开放式基金进行绩效评价,以期对该领域的研究提供一种新的思路与方法。
2 模型的建立我国目前绝大部分是利用三因子模型对基金的投资风格进行评价分析, 运用多因子模型的研究较少, 因此本文试图将多因子模型引入开放式基金绩效评价领域, 以丰富现有的研究理论与方法。
2.1 三因子模型三因子模型公式如下:
| $ \begin{array}{l} {R_{it}} - {R_{Ft}}{\rm{ = }}{a_i} + {b_i}\left( {{R_{Mt}} - {R_{Ft}}} \right) + {s_i}{\rm{SM}}{{\rm{B}}_t} + \\ {h_i}{\rm{HM}}{{\rm{L}}_t} + {e_{it}}。\end{array} $ | (1) |
其中, Rit表示股票或投资组合i在第t期的股票收益率, RFt表示无风险收益率, RMt表示市值加权的市场组合收益率, (RMt-RFt)表示市场风险溢价因子, SMBt表示市值因子, HMLt表示账面市值比因子, eit表示残差。
2.2 多因子模型Fama与French在三因子模型的基础上, 引入盈利能力因子RMWt与投资水平因子CMAt构建了多因子模型[8]:
| $ \begin{array}{l} {R_{it}} - {R_{Ft}} = {a_i} + {b_i}\left( {{R_{Mt}} - {R_{Ft}}} \right) + {s_i}{\rm{SM}}{{\rm{B}}_t} + \\ {h_i}{\rm{HM}}{{\rm{L}}_t} + {r_i}{\rm{RM}}{{\rm{W}}_t}{\rm{ + }}{c_i}{\rm{CM}}{{\rm{A}}_t} + {e_{it}}。\end{array} $ | (2) |
由于基金投资组合中的十大重仓股对基金整体的绩效具有重要的影响(Kothari and Warner, 2001[14]; 刘莎莎等, 2013[15]), 因此选择以十大重仓股的业绩表现为切入点, 进而对开放式基金的绩效作出评价。
首先基于多因子模型, 借助沪深市场的截面数据, 拟合出多因子模型(2)中的系数bi,si,hi,ri,ci及截距ai; 其次以中国证监会2012年《上市公司行业分类指引》为标准, 将沪深市场分为19个行业类别。用个股的总市值加权平均市场年收益率、年末总市值/行业年末总市值、股东权益/年末总市值、净利润/年末总市值、投资收益率分别近似多因子模型中的市场风险溢价因子(RMt-RFt)、市值因子SMBt、账面市值比因子HMLt、盈利能力因子RMWt与投资水平因子CMAt, 将上述指标分别代入多因子模型, 与拟合出的系数相乘, 即可近似出各行业个股的理论收益率, 即超额收益率(Rit-RFt); 最后依据个股的理论收益率, 对各行业的股票进行收益率排名, 即可得到各行业排名前十的股票。以多因子模型为例, 具体操作如下:构造多因子模型矩阵X、系数矩阵β以及市场风险溢价因子矩阵Y。
| $ \begin{array}{l} \mathit{\boldsymbol{X}} = \\ \left[ {\begin{array}{*{20}{c}} 1&{{{\left( {{R_M} - {R_F}} \right)}_1}}&{{\rm{SM}}{{\rm{B}}_1}}&{{\rm{HM}}{{\rm{L}}_1}}&{{\rm{RM}}{{\rm{W}}_1}}&{{\rm{CM}}{{\rm{A}}_1}}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&{{{\left( {{R_M} - {R_F}} \right)}_k}}&{{\rm{SM}}{{\rm{B}}_k}}&{{\rm{HM}}{{\rm{L}}_k}}&{{\rm{RM}}{{\rm{W}}_k}}&{{\rm{CM}}{{\rm{A}}_k}} \end{array}} \right], \end{array} $ | (3) |
k为该行业股票数
| $ \mathit{\boldsymbol{\beta = }}\left[ \begin{array}{l} {a_i}\\ {b_i}\\ {s_i}\\ {h_i}\\ {r_i}\\ {c_i} \end{array} \right] $ | (4) |
| $ \mathit{\boldsymbol{Y}} = \left[ \begin{array}{l} {\left( {{R_i} - {R_F}} \right)_1}\\ \vdots \\ {\left( {{R_i} - {R_F}} \right)_k} \end{array} \right] $ | (5) |
构造残差平方和函数:
| $ S\left( \mathit{\boldsymbol{\beta }} \right) = {\left\| {\mathit{\boldsymbol{X\beta }} - \mathit{\boldsymbol{Y}}} \right\|^2} $ | (6) |
对S(β)进行微分取最小值, 可得到
| $ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X\beta }} = {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (7) |
根据式(3)~(7), 得到样本的拟合系数矩阵β。假设投资组合P中十大重仓股的实际收益率为pi, 重新构建投资组合Q的十大重仓股收益率为qi, 各重仓股占基金资产总值的份额比例为βi, 衡量实际收益率偏离基准的程度为f, 则
| $ f = \sum\limits_{i = 1}^{10} {\left( {\left( {{p_i} - {q_i}} \right)\frac{{{\beta _i}}}{{\sum\limits_{i = 1}^{10} {{\beta _i}} }}} \right)} $ | (8) |
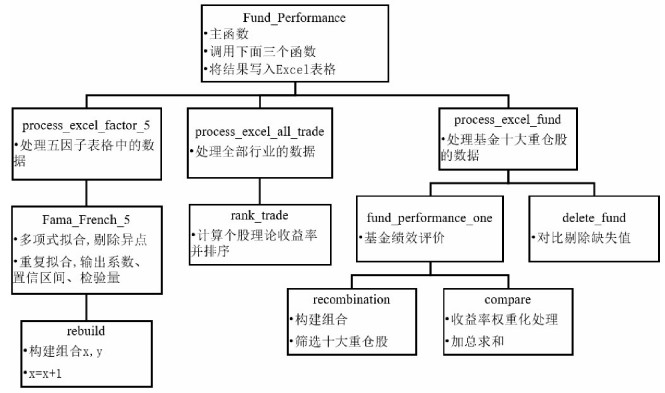
将股票型开放式基金投资组合P中的十大重仓股的实际收益率与各行业排名前十的股票相对比, 将低于理论收益率的股票进行替换, 从而构建出十大重仓股的理论化投资组合Q, 并以其作为基准组合; 利用投资组合P的实际收益率pi与理论投资组合Q的收益率qi, 代入差值模型(8), 计算实际投资组合P偏离基准组合Q的程度f; 根据f的大小, 对股票型开放式基金进行排名, 从而形成一套动态的评价体系。见图 1。
|
图 1 股票型开放式基金绩效评价流程 Fig. 1 The performance evaluation process of stock type open-ended fund |
本文选取了Wind数据库中603只股票型开放式基金作为研究样本, 研究区间为2016年1月1日至2016年12月31日。选取投资组合类型为2*3组合划分下的总市值加权的市场风险溢价因子、市值因子、账面市值比因子、盈利能力因子与投资水平因子的日度化数据, 来自CSMAR数据库。总市值加权平均市场年收益率、年末总市值/行业年末总市值、股东权益/年末总市值、净利润/年末总市值、投资收益率等年度化指标来自RESSET金融数据库, 选取年化净资产收益率作为十大重仓股的实际收益率pi, 十大重仓股占基金总资产的份额比例βi来自Wind数据库。无风险利率基准为中国人民银行颁布的一年定期存款利率, 日度化无风险利率是根据复利计算方法, 将年度无风险利率转化为日度数据。
3.2 模型检验 3.2.1 三因子模型检验假设:
H0:bi=si=hi=0
H1:bi,si,hi不全为0
检验结果见表 1。
|
|
表 1 假设检验结果(三因子模型) Tab. 1 Hypothesis testing results(three-factor model) |
|
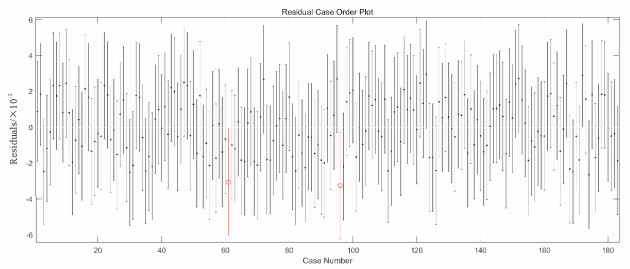
图 2 三因子模型残差图 Fig. 2 Three-factor model residual graph |
三因子模型的拟合回归结果如下所示:
Rit-RFt=4.341 3e-4+1.0724(RMt-RFt)-0.498 4SMBt+0.436 89HMLt+eit
3.2.2 多因子模型检验假设:
H0:bi=si=hi=ri=ci=0
H1:bi,si,hi,ri,ci不全为0
检验结果见表 2。
|
|
表 2 假设检验结果(多因子模型) Tab. 2 Hypothesis testing results(multi-factorial model) |
通过上述检验结果得知, p < α, F(1, n-2), 1-α < F, 在5%显著性水平上拒绝原假设, 接受备择假设, 说明回归检验出来的系数是显著的。残差图中的异常点较多, 作为拟合优度的r2=0.972 1, 当其越接近于1, 表明其拟合程度越可靠。通过剔除残差图中的异常点再次进行拟合, 从而提高拟合的可靠程度。结果见表 3。
|
|
表 3 线性拟合结果(多因子模型) Tab. 3 Linear fitting results(multi-factorial model) |
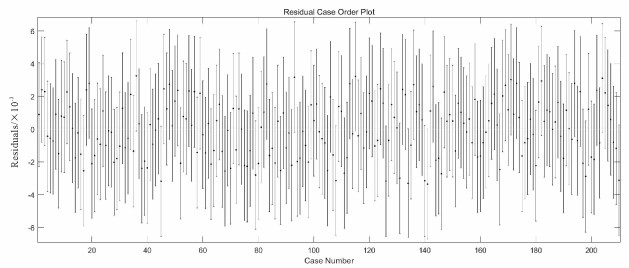
根据以上数据可知, p < α, F(1, n-2), 1-α < F, 在95%置信水平上拒绝原假设, 接受备择假设, 说明回归检验出来的系数是显著的。r2=0.984, 拟合结果较之前有所改善, 异常点减少, 回归模型的拟合精度变高。
|
图 3 多因子模型残差图 Fig. 3 Multi-factorial model residual graph |
综上所述, 多因子模型的拟合回归结果如下所示:
Rit-RFt=-1.578 8e-5+1.070 9(RMt-RFt)-
0.541 45SMBt+0.307 17HMLt+
0.060 608RMWt+0.519 02CMAt+eit
3.3 基金绩效评价由于本文选取的样本数量过多, 篇幅限制, 只展现出排名前20的基金绩效排名结果, 具体见表 4、表 5。
|
|
表 4 开放式基金绩效排名(三因子模型) Tab. 4 Open-end fund performance ranking(three-factor model) |
|
|
表 5 开放式基金绩效排名(多因子模型) Tab. 5 Open-end fund performance ranking(multi-factorial model) |
根据表 4,5排名表可得:当实际投资组合P偏离基准组合Q的程度f为正时, 说明基金实际的投资组合表现优异; 当f为负时, 说明基金实际的投资组合表现较差。在对603只股票型开放式基金进行绩效排名发现, 排名前102的基金的f值为正, 占总数的1/3, 而之后2/3的基金的f值为负, 说明其投资组合表现低于理论组合, 基金经理人普遍缺乏控制风险的能力, 基金的实际投资风格趋同, 具有明显的“羊群效应”。
对比两个排名表, 我们可以发现:①无论是三因子模型还是多因子模型, 基金001195.OF、基金159948.OF和基金159915.OF都排在了前三名。②考虑到盈利能力因子RMWt与投资水平因子CMAt因素, 基金110022.OF和基金161213.OF等的排名会略有调整。③基金530018.OF等在多因子模型中排进了前20名, 但是在三因子模型中没有排进20名。由此可见, 引入盈利能力因子RMWt与投资水平因子CMAt两个因素, 会更加准确且全面地评价基金的优劣。
本文借助多因子模型, 拟合出我国证券市场的多因子系数。与此同时, 还利用相同的方法拟合出了三因子模型的系数, 并将两部分数据加以对比。其中, si=-0.498 4(三因子模型)、si=-0.541 45(多因子模型), 该系数衡量开放式基金的大小盘属性, 拟合出的结果为负, 说明样本基金在两种模型中均具有大盘投资的风格倾向。同时重新对十大重仓股进行投资组合, 构建差值模型, 根据样本基金偏离基准的程度f, 对开放式基金进行绩效排名。2/3的样本基金f为负, 说明大部分基金实际的投资组合收益较差, 具有显著的投资趋同现象, 基金经理人并不具备应对市场风险的能力, 投资选股能力较差, 我国基金在总体上并未超越市场平均收益率。
| [1] |
MARKOWITZ H. The utility of wealth[J]. Journal of Political Economy, 1952, 60: 151. DOI:10.1086/257177 |
| [2] |
TREYNOR J, TREYNOR J. How to Rate Management of Investment Funds[M]//Treynor on Institutional Investing.New Jersey: John Wiley & Sons, Inc. 1965: 6-6.
|
| [3] |
SHARPE W F. Mutual Fund Performance[J]. Journal of Business, 1965, 39(1): 119-138. |
| [4] |
JENSEN M C. The Performance of mutual funds in the period 1945-1964[J]. The Journal of Finance, 1968, 23(2): 389-416. DOI:10.1111/j.1540-6261.1968.tb00815.x |
| [5] |
SHARPE W F. Capital asset prices:A theory of market equilibrium under conditions of risk[J]. The Journal of Finance, 1964, 19(3): 425-442. |
| [6] |
FAMA E F, FRENCH K R. Common risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics, 1993, 33(1): 3-56. DOI:10.1016/0304-405X(93)90023-5 |
| [7] |
CARHART M M. On persistence in mutual fund performance[J]. The Journal of Finance, 1997, 52(1): 57-82. DOI:10.1111/j.1540-6261.1997.tb03808.x |
| [8] |
FAMA E F, FRENCH K R. A five-factor asset pricing model[J]. Journal of Financial Economics, 2015, 116(1): 1-22. DOI:10.1016/j.jfineco.2014.10.010 |
| [9] |
屠新曙, 朱梦. 基金绩效评价的Fama-French三因素模型检验[J]. 金融经济学研究, 2010, 25(1): 103-112. |
| [10] |
许永峰, 赵小玥, 赖雨恒, 等. 一种新的开放式基金绩效评价方法[J]. 西北大学学报(自然科学版), 2015, 45(4): 525-531. |
| [11] |
齐岳, 孙信明. 基于投资策略的基金绩效评价——以价值、成长和平衡型基金为例[J]. 管理评论, 2016, 28(4): 155-165. |
| [12] |
赵胜民, 闫红蕾, 张凯. Fama-French五因子模型比三因子模型更胜一筹吗——来自中国A股市场的经验证据[J]. 南开经济研究, 2016(2): 41-59. |
| [13] |
宋光辉, 董永琪, 陈杨炀, 等. 中国股票市场流动性与动量效应——基于Fama-French五因子模型的进一步研究[J]. 金融经济学研究, 2017(1): 36-50. |
| [14] |
KOTHARI S P, WARNER J B. Evaluating mutual fund performance[J]. The Journal of Finance, 2001, 56(5): 1985-2010. DOI:10.1111/0022-1082.00397 |
| [15] |
刘莎莎, 刘玉珍, 唐涯. 信息优势、风险调整与基金业绩[J]. 管理世界, 2013, 239(8): 67-76. |
 2018, Vol. 48
2018, Vol. 48
