出于政治原因考虑, 汉诺威家族在德国哲学家、数学家莱布尼茨(Gottfried Wilhelm Leibniz, 1646—1716)去世后就完整封存了其档案。而在二战期间, 希特勒(Adolf Hitler, 1889—1945)曾安排了一辆虎式坦克看守汉诺威莱布尼茨文献馆。故有关莱布尼茨的原始资料保存完好, 甚至现在还能找到其当年的病假条。1985年系统整理莱布尼茨文档工作纳入德国科学院计划, 《莱布尼茨全集》正逐册出版, 预计出版120卷。因商榷中文版《莱布尼茨全集》相关事宜, 本文第一作者有幸结识了德国柏林-勃兰登堡科学院《莱布尼茨全集》编辑部主任李文潮先生, 并应邀参加了2017年中德莱布尼茨国际研究会(作大会报告), 获得了一些第一手珍贵资料。本文拟在前人研究基础上^[1-3], 在哲学视野下以“为什么微积分”为切入点, 分析莱布尼茨部分数学手稿中的创新数学思想, 探赜大师的“思想魅力”和“火热思考”。

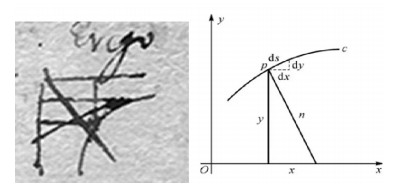
1 微分学之创新火花 1.1 洞察微分本质

在莱布尼茨众多手迹中, 最令人叹服的是其1673年11月11日(可见, 1675年中的“5”后被改成“3”)所写数学手稿。其中给出了微分学基本思想:试把曲边梯形分割成许多小矩形, 每个小矩形与曲线之间微小直角三角形两边分别是曲线上相邻两点的纵坐标和横坐标之差。当这两个差均无限减小时, 曲线上相邻两点则无限接近^[4]。莱布尼茨用dx表示两个相邻x值之差, 用dy表示相邻y值之差, 即曲线上相邻两点纵坐标之差, 并称之“微差”。他认为dy和dx可任意小, 并构造出一个包含dx, dy的“特征三角形”, 体现了“以直代曲”的创新思想。他写道:横坐标x的微分dx是个任意量, 而纵坐标y的微分dy则可定义为它与dx之比等于纵坐标与次切距之比。即

$ {\rm{d}}s/n = {\rm{d}}x/y = {\rm{d}}y/x $

因y与次切距之比就是切线斜率, 故该定义与导数定义一致。但莱布尼茨未给出严格切线定义, 只是说“求切线就是画一条连接曲线上距离为无穷小的两点之间的直线。”用现代数学语言可表述为, 切线是割线的极限位置。

籍此, 1684年10月莱布尼茨在莱比锡《教师学报》(Acta Eruditorum)发表了论文《一种求极值和求切线的新方法, 亦能应用于分数和无理量情形及非寻常类型的有关计算》(Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationals quantitates moratur, et singular pro illi calculi genus。简记《新方法》)。尽管全文只有6页, 且理论尚不成熟, 论证也不太严谨, 但却具有里程碑似的重要历史意义, 因为这是数学史上第一篇正式发表的微分学文献。此乃莱布尼茨对1673年以来其微分学研究的概括总结, 着重介绍了微分定义、运算法则及曲线的极值、拐点等问题^[5]。

史料表明:早在1666年，莱布尼茨就考察了平方数序列各阶之差, 他将此与微分相联系:一阶差相当于dy, 其和等于y。这种和与差间的互逆性, 与依赖于坐标之差的切线问题及依赖于坐标之和的求积问题之互逆性是一样的。故他在考虑无穷小量和差运算时, 已将其与有限量和差可逆性关系的研究相互联系起来。

在求量之差时, 莱布尼茨初用“x/d”表示对x的微分, 即表示求差就会引起量的逐次降低, 若同时出现不同阶微分时, 则只留下最低阶, 去掉所有高阶。后他又用“dx”来代替“x/d”。并给出一系列微分基本公式, 如微分公式:

$ {\rm{d}}\left( {xy} \right) = x{\rm{d}}y + y{\rm{d}}x $

(2)

在推导过程中, 分别给变量x, y一个微小增量dx, dy, 则

$ (x + {\rm{d}}y)(y + {\rm{d}}y) = x{\rm{d}}y + y{\rm{d}}x + {\rm{d}}x{\rm{d}}y + xy $

于是

$ \begin{array}{l} {\rm{d}}\left( {xy} \right) = (x + {\rm{d}}x)(y + {\rm{d}}y) - xy = \\ \;\;\;\;\;\;\;\;\;\;\;\;x{\rm{d}}y + y{\rm{d}}x + {\rm{d}}x{\rm{d}}y \end{array} $

因dxdy是比xdy+ydx高一阶的无限小量, 可以舍去, 故d(xy)=xdy+ydx。

莱布尼茨宣称运用微分基本运算法则, 可得整指数幂导数公式dxⁿ=nx^n-1dx。并断定, 当n取任意实数时结论仍成立。后又推出指数、对数等超越函数的微分公式^[6]。

1.2 泰勒公式还是莱布尼茨公式

从图 3手稿可看出, 莱布尼茨熟悉幂级数展开式, 并写出收敛于$ \sqrt 2 $的无穷级数(文字为拉丁文), 这应是泰勒公式初等形式。

虽然现尚不清楚该手稿书写的具体日期，但可推测$ \sqrt 2 $展开式应是莱布尼茨独立推出，而未受到泰勒(B.Taylor, 1685—1731)的影响。这主要从历史事件上推测, 1699年初英国皇家学会开始指控莱布尼茨剽窃了牛顿(Isaac Newton, 1642—1727)微积分成果，相关争论在1711年几乎全面爆发。泰勒最早是在1712年书信给友人告知其研究成果，而于1715年出版的《正和反的增量法》中第一次公开陈述了泰勒公式(未考虑级数收敛性)。故从时间上看泰勒公式公开发表之时，正是微积分优先权争执激烈时期，牛顿学派不会和莱布尼茨学派交流其研究成果，为了避嫌莱布尼茨更不会应用牛顿学派的成果。这样一来，该手稿书写应该早于1715年，若是此推测成立的话，泰勒公式应该冠名为莱布尼茨公式。

在这里, 莱布尼茨可取$ f\left( x \right) = {\left( {1 + x} \right)^{\frac{1}{2}}}$, 根据公式:

$ \begin{array}{l} f\left( x \right) = f\left( {{x_0}} \right) + \frac{{f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)}}{{1!}} + \\ \frac{{f''\left( {{x_0}} \right){{\left( {x - {x_0}} \right)}^2}}}{{2!}} + \ldots + \frac{{{f^{(n)}}\left( {{x_0}} \right)\left( {x - {x_0}} \right)}}{{n!}} + \\ o[\left( {x - {x_0}} \right)^n] \end{array} $

取x=1, x₀=0,

$ \begin{array}{l} \;\;\;\sqrt {1 + x} = 1 + \frac{1}{2}x - \frac{1}{{2.4}}{x^2} + \frac{{1 \cdot 3}}{{2 \cdot 4 \cdot 6}}{x^3} + \ldots \\ + {\left( { - 1} \right)^{n - 1}}\frac{{\left( {2n - 3} \right)!!}}{{\left( {2n} \right)!!}}{x^n} + \ldots , \left( { - 1 \le x \le 1} \right), \end{array} $

代入计算得到结果。从展开式可见, 莱布尼茨未应用阶乘符号, 数与数相乘以“·”来表示。用符号“×”代表乘号是由英国数学家奥特雷德(W. Oughtred, 1574—1660)首创, 他于1631年出版的《数学之钥》中引入该记法。乘号曾有过10余种表达形式, 现在通用的只有两种。用“·”表示乘号源于英国数学家哈里奥特(T. Harriot, 1560—1621)。莱布尼茨认为, “×”有些像拉丁字母“X”, 故反对其作为乘法符号, 倡议用“·”表示乘号。还提出用“∩”表示相乘, 该符号现广泛应用于集合论。

莱布尼茨在展开式中应用了等号。“=”最早出现于英国数学家雷科德(R. Recorde, 1510—1558)的《砺智石》, 源自“世上没有比两条平行线更相似”。但当时欧洲关于符号“=”还有其他含义, 如韦达(Francois Viète, 1540—1603)表示两个数字之差, 还有人表示小数点, 如316.857写成316=857。而笛卡儿(René Descartes, 1596—1650)则应用符号∝表示等号。

莱布尼茨的根号书写与现代稍有不同。在1480年前后, 德国人曾用“·”表示平方根, 如·3表示$ \sqrt 3 $，至16世纪初, 小点带上了一条小尾巴, 这许是书写快时所致, 籍此逐渐演变成了“√”。如1525年, 鲁道夫(C.Rudoff)在其《求根式》中用√8表示$ \sqrt 8 $。莱布尼茨的书写形式与他相同, 大概是借鉴其经验。实际上, 笛卡儿在1637年第一个使用了根号√，他为了防止被开方数较多, 上面加了一条横线, 并且比鲁道夫多了一个小钩, 这样看上去更为美观。可推测, 莱布尼茨应看到了笛卡儿的符号表示，但他未采用笛卡儿的根号表示。

另展开式中还有分号的使用, 在现在亦可理解为乘积之意。

2 积分学之灵光闪现

简而不凡的数学符号具有神奇科学力量, 一旦释放能产生几乎爆炸般威力。莱布尼茨所创建的一系列优美微积分符号就具有这般功效。他谨慎引入每一个数学符号, 总是选择富有启发性的符号, 以“最大限度减少人的思维劳动”。如他曾用类似根号符号来表示积分, 并带有小尾巴“d”, 在图 4中, 对于3~5式, 莱布尼茨拟求累次积分, 其把积分号变长, 把第一步积分函数写在里面, 并配上dx, 他未区分积分变量, 均以x表之, 且用xx表示x², 但三次幂莱布尼茨选用了现代符号表示。应用现代积分符号所给9个积分式为(其中第2式由作者推测而来, 从上下文来看, 第5式积分变量应是y):

$ \begin{array}{l} y\mathop = \limits^{(2)} \smallint y{\rm{d}}x, \\ y\mathop = \limits^{(3)} \smallint (\smallint y{\rm{d}}x){\rm{d}}x, \\ y\mathop = \limits^{(4)} \smallint (\smallint (\smallint y{\rm{d}}x){\rm{d}}x){\rm{d}}x, \\ y\mathop = \limits^{(5)} \smallint (\smallint (\smallint (\smallint y{\rm{d}}x){\rm{d}}x){\rm{d}}x){\rm{d}}x, \\ \int_0^x {{\rm{d}}x\mathop = \limits^{(6)} x, } \\ \int_0^x {(\int_0^x {{\rm{d}}x){\rm{d}}x\mathop = \limits^{(7)} \int_0^x {x{\rm{d}}x\mathop = \limits^{(8)} \frac{1}{2}{x^2}, } } } \\ \int_0^x {(\int_0^x {(\int_0^x {{\rm{d}}x){\rm{d}}x){\rm{d}}x\mathop = \limits^{(9)} \int_0^x {\frac{1}{2}{x^2}{\rm{d}}x\mathop = \limits^{(10)} \frac{1}{{2 \cdot 3}}{x^3}} } } } \end{array} $

此时，莱布尼茨对微积分研究已较深入, 符号也有了雏形。同时印证了其所讨论积分为定积分^[7]。在图 5手稿中, 莱布尼茨以变量x为分界线, 向右依次求对x的定积分、二重积分和三重积分, 注意到积分号下没有dx; 向左依次求对x的一阶、二阶和三阶微分, 注意到微分符号采用dd和ddd。第二行为第一行的计算结果, 呈现出经微分和积分运算后未知数x幂的齐次变化规律性。第三行的排列更能看出规律, 对x微分次数越多, 其次数越小, 而对x积分次数越多, 其次数越大。从指数为负整数到零, 再到正整数, 分别对应着微分运算、元变量和积分运算, 进一步印证了莱布尼茨关于微分和积分是一对互逆运算的新发现。只有确立了这一基本运算关系, 才能构建出系统的微积分理论。他还推广到对各种函数的微分和求积运算, 从中总结出共同的算法程序和数学规律, 使得微积分方法普遍化, 进而发展成用符号表示的微积分运算法则。

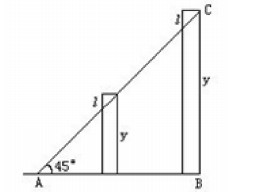
1686年, 莱布尼茨又在《教师学报》发表论文《论一种深奥几何学与不可分量及其无穷分析》(De geometria recondita et analysi indivisibilium atque infinitorum)。该文以讨论积分学为主, 谓之《新方法》续篇^[8]。

莱布尼茨用纵坐标y表示平面曲线同坐标轴围成的曲边梯形面积(说明$ y\mathop = \limits^{\left( 2 \right)} \smallint y{\rm{d}}x $的正确性)。这样所形成曲边梯形面积变量便与曲线纵坐标构建了联系。他首先从最简情形y=x开始, 以x表示相邻两项次序, 序数差为1, 设l为相邻两项实际差。用拉丁文omnia缩写omn表示求和, 记为omn.l=y(即y=∫ dy), 则omn.l就表示首项为0的序列一阶差之和。即当l很小时, 其和就是三角形ABC面积“y²/2”, “从0起逐渐增长的直线, 每一个用与它相应增长元素相乘, 组成一个三角形。”再次印证莱布尼茨所讨论积分是定积分, 尽管未明确给出上下限, 但积分区间是为0到y。

莱布尼茨先用“Sydx”表示, 后改为“∫”表示积分符号, 显然其是“Sum”的第一个字母“S”的拉伸。他在手稿中写有若干积分计算。

由于莱布尼茨从有限差值开始无穷小运算, 故他最初曾试图将实无穷小代之以与其成比例的有限数量, 即不用dx，dy本身, 而用比值dy/dx。他曾以为把dx，dy看成有限量, 不严密问题就解决了。但dy/dx同样需要说清dx，dy含义。故莱布尼茨提出用“充分大”和“充分小”代替无穷大和无穷小, “我们可不用无穷大、无穷小, 而用充分大和充分小的量, 使得误差小于给定误差限度, 故我们和阿基米德方式的不同之处仅仅在于表述, 而我们的表达更为直接, 更适于发明家艺术。” ^[9]

为此, 莱布尼茨不得不诉诸于物理或几何模型, 应用现实中量的不同层次相对性诠释无穷大和无穷小。“当谈到不同阶的无穷大与无穷小时, 就像对恒星距离而言, 把太阳看作一个点; 而对地球半径而言, 则把普通球看作一个点。这样, 恒星距离对于普通球半径而言是无穷的无穷大, 或无穷倍的无穷大。”而“若你不承认无限长、无限短线段具有形而上学的严密性, 也不承认它们是实际东西, 则你一定可把它们当作一种能够缩短论证思想的东西来使用, 正如在普通分析中使用虚根一样, 我不十分相信除了把无限大、无限小看作理想东西, 看作有根据的假设, 还有什么必要去考察他们。”甚至“我不相信确有无限大量和无限小量存在, 它们只是虚构, 但对于缩短论证和在一般叙述中则是有用的虚构。”^[10]

可见, 莱布尼茨仅是把微积分当作一种数学运算方法, 只要按照该方法去计算, 就能得出正确结果, 而不必关心其基本理论概念。正是这种理论上的不严谨、不严密, 使人对“无穷小”认识模糊, 其既不是有限量, 也不是无限小, 又不是零, 难道是消逝量的鬼魂?进而导致了第二次数学危机。事实上, 莱布尼茨对于微积分理论基础的这种看似冒失的大胆相信态度, 反倒可能促进了微积分及其应用的迅速发展。

3 其他数学手迹

莱布尼茨治学风格从其文稿可窥一二, 从中所表现出来的富有创造性、跳跃化的思维使人惊叹不已, 而其符号化思维常常又带有某种神秘性, 使得读者小心翼翼。他好像不过分追求结果的准确性, 例如连分数的计算(见图 7), 而更执着于数学推导过程, 他会把他的思考或作题过程一步一步地展现出来, 他富有想象、粗线条式的思维让他在微积分的世界里天马行空、自由翱翔, 而文稿内容在现在看来还不够严谨、不合理、难以理解的地方, 在这位伟大的数学家的眼里根本就是脚下的一粒沙子, 一脚就踏过去了, 而后来的读者却要在这个地方纠缠困惑不止, 如其坚定支持者约翰·伯努利(John Bernoulli, 1667—1748)所说, “如其说是解释, 不如说是谜。”^[11]

连分数结果实际为$ \frac{{137\;629}}{{4\;307}} \approx 31.9547248664964012 $, 而如下连分数等于右边实际为$31\frac{1}{{1 + \frac{1}{{2 + \frac{1}{{9 + \frac{1}{{4 + \frac{1}{{2 + \frac{1}{{1 + \frac{1}{{22}}}}}}}}}}}}}} = \frac{{4290000}}{{135424}} \approx 31.6782844990548204 $

莱布尼茨曾与数百人有着书信交流, 其中既有名流也有凡夫。今仍能从中找到雅各布·伯努利(Jacob Bernoulli, 1654—1705)等人寄来的“随笔短笺”。莱布尼茨对数学问题的探讨, 绝大部分都体现在通信中。如莱布尼茨与约翰·伯努利从1694年开始通信, 一直保持到1716年。在长达20余年的通信中, 他们主要讨论了数学和物理学问题及其与形而上学之联系^[12]。

4 余论

莱布尼茨的博学多才罕有所比，其研究领域涉及诸多学科。他不仅从哲学视角对数学本质进行了诠释，还醉心于微积分研究，沟通了微分学和积分学的相互联系，并创建了一系列优美的数学符号。

对于数学性质，莱布尼茨认为，数学(主要指算术和几何学)是一种真理，它是以一种潜在方式存在于我们心中，是具有天赋性之学科。可通过考虑其来源而进行学习，或采用经验证实的方式进行学习。莱布尼茨否认“凡是人所学到东西都不是天赋的”。数学命题的观念是天赋的，这样天赋不是就其现实知识而言，而是指潜在知识是天赋的，数学知识的获得并非依靠感觉材料，在数学知识产生过程中，感觉经验只起到“暗示、证实和确认”的作用。他认为，以数为研究对象的算术就蕴含诸事物的各种动力，成为宇宙的静力学。数学天赋性及数学研究对象的形而上学性使得数学具有一种崇高且重要地位^[13]。

莱布尼茨指出，数学是人类推理杰作，不仅可改变普通人生活方式，也能使得政治制度更加完善，且可提升人类理解度甚至消除我们与世俱来的恶。故莱布尼茨数学化思想是以数学理论为基础并超越了数学方法，是一种形式化、模式化、严谨的逻辑思维方式。莱布尼茨科学奋斗目标是寻求一种可获得知识和创造发明的普遍方法，正是这种努力导致其诸多科学发现。他倡议社会科学与数学科学进行类比，并将数学原理应用于社会科学研究之中^[14]。其一系列重要数学理论为近现代数学发展奠定了基础。他曾讨论负数和复数性质，探讨线性方程组消元法，并首次引入行列式概念, 创立符号逻辑学基本概念，发明二进制和能进行四则运算及开方运算的计算机等，当然翘楚还是创立微积分。正是微积分的创建使得数学变得更加美妙、奇妙，且极大拓展了数学疆域^[15]。